神経ネットワークの自己組織化臨界現象を調べる上で、global lability of synchronization(同期のグローバルな不安定性)法という手法を使うことになったので、その計算方法をメモしておく。
大まかにいうと、ある神経ネットワークの活動において時刻$t$で同期しているニューロンのペアの個数$M(t)$と時刻$t+1$で同期しているペアの個数$M(t+1)$がどれだけ違うか、ということを評価する。値が大きければ大きいほど全体の同期/非同期プロセスを表し、小さいほど局所的なものを表す。
位相同期の評価
時系列データとして、二つの信号$s_i(t)$と$s_j(t)$の二種類が与えられたとする。
この二つの信号がある時刻$t$において
- 位相差$\theta_{i, j}(t)$の絶対値が$\pi/4$未満である
- 時間窓$v$の範囲での位相差$\theta_{i, j}(t)$に対する同期パラメータ$\gamma_{i,j}(t)$が$\sqrt{1/2}$より大きいこと
この二つの条件を満たす時、二つの信号は同期しているとする。
ここで位相差$\theta_{i, j}(t)$は以下のように計算を行う。
$$ \Delta \theta_{i,j}(t)=\arctan[{\tilde s_i(t)s_j(t)- \tilde s_j(t)s_i(t)\over s_i(t)s_j(t)- \tilde s_j(t)\tilde s_i(t)}] $$
ここで$\tilde s(t)$は信号$s(t)$のヒルベルト変換を表す。
$$ \tilde s(t) = {1\over \pi}\int^\infty_{-\infty} {s(\tau)\over t-\tau} d\tau$$
ヒルベルト変換って何?という方は以下↓
参考: https://www.onosokki.co.jp/HP-WK/eMM_back/emm180.pdf
ざっと言うと実部のみの信号$s(t)$が本来含む虚部の信号$\tilde s(t)$を返す操作。さらに大雑把に言えば位相を90°ずらす操作に当たるらしい。
同期パラメータ$\gamma_{i,j}(t)$は以下のように求める。
$$ \gamma_{i,j}(t) = \sqrt{[{1\over v}\sum^{t+v}_t \cos \Delta \theta _{i,j}(t)]^2+[{1\over v}\sum^{t+v}_t \sin\Delta \theta _{i,j}(t)]} $$
ここで$v$は時間窓を表す。
ネットワークの中の全てのニューロン信号について、これらの条件を満たす一致するペアの個数を$M(t)$とする。以下のような式で表すことができる。
$$ M(t)=\sum[|\Delta \theta_{i,j}|<\pi/4 ~and ~ \gamma_{i,j}(t)>\sqrt{1/2}] $$
不安定性の評価
得られたペアの個数$M(t)$と$M(t+1)$から、以下のようにして不安定性$l(t)$を求めることができる。
$$ l(t) = |M(t+1)-M(t)|^2 $$
実装
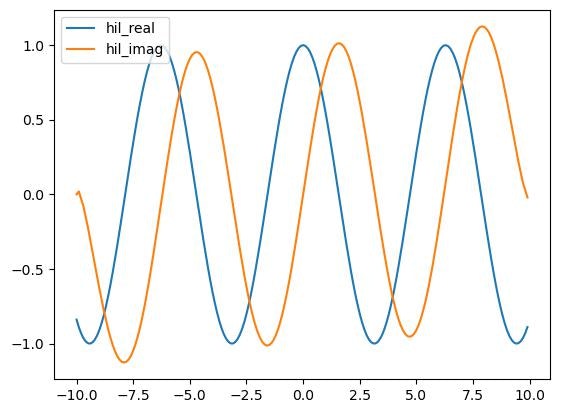
前提として、ヒルベルト変換は以下のように計算することができる。
import matplotlib.pyplot as plt
import numpy as np
from scipy.signal import hilbert
x = np.arange(-10,10, 0.1)
y = np.cos(x)
z = hilbert(y)
plt.plot(x,z.real, label="hil_real")
plt.plot(x,z.imag, label="hil_imag")
plt.legend()
plt.show()
元の入力であるcos波に対して虚部であるsin波が取得できていることがわかる。
これを用いて実装を行ったのが以下のクラス。
import itertools
import matplotlib.pyplot as plt
import numpy as np
from scipy.signal import hilbert
class DLS():
def __init__(self, signals, v=50):
self.signals = [hilbert(s) for s in signals]
self.v = v #時間窓を50ステップとする
def theta(self, s1, s2, t_i):
y = s1[t_i].imag*s2[t_i].real - s2[t_i].imag*s1[t_i].real
x = s1[t_i].real*s2[t_i].real - s1[t_i].imag*s2[t_i].imag
return np.arctan(y/x)
def gamma(self, i, j, t_i):
if t_i + self.v >= len(self.signals[i]):
return 0
T_i = np.arange(t_i, t_i+self.v)
cos_ave = np.cos(self.theta(self.signals[i], self.signals[j], T_i)).sum()/len(T_i)
sin_ave = np.sin(self.theta(self.signals[i], self.signals[j], T_i)).sum()/len(T_i)
return np.sqrt(cos_ave**2 + sin_ave**2)
def isPair(self, i, j, t_i):
theta_abs = abs(self.theta(self.signals[i], self.signals[j], t_i))
gamma = self.gamma(i,j,t_i)
if theta_abs < np.pi/4 and gamma > np.sqrt(1/2):
return 1
else:
return 0
def M(self, t_i):
count = 0
for i, j in itertools.combinations(range(len(self.signals)), 2):
count += self.isPair(i, j, t_i)
return count
def l(self, t_i):
return (self.M(t_i+1)-self.M(t_i))**2
試しに全く同じsin波を3つ入れて計算してみる。
v = 50
x = np.sin(np.arange(0,10, 0.1))
signals = [x, x, x]
dls = DLS(signals, v)
for i, x in enumerate(x[:v]):
print(dls.M(i))
# 一致する組み合わせ数3が出力される
print(dls.l(i))
# 完全に安定なので0が出力される
こうして計算を行うことができた。
参考文献
Kitzbichler, M. G., Smith, M. L., Christensen, S. R., & Bullmore, E. (2009). Broadband criticality of human brain network synchronization. PLoS computational biology, 5(3), e1000314.
Aguilar-Velázquez, D., & Guzmán-Vargas, L. (2019). Critical synchronization and 1/f noise in inhibitory/excitatory rich-club neural networks. Scientific reports, 9(1), 1-13.