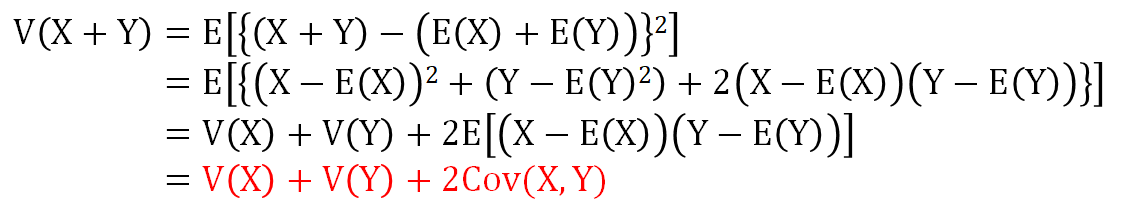はじめに
ふと、材料AとBを接合した後の寸法誤差はどうなるんだっけ・・・と思い復習しました。
導出
簡単のために以下のように記号を定義します。
X：確率変数、確率で変動するAやBの寸法と考えると分かりやすいです。
E(X)：確率変数Xの期待値
V(X)：確率変数Xの分散
Cov(X,Y)：確率変数Xと確率変数Yの共分散
2つの確率変数の和の期待値は簡単です。
次に分散ですが、以下のように式変形していきます。
結論として、材料AとBの寸法の共分散が0であれば、それぞれの分散を足すだけで良いです。
共分散Conv(X,Y)は、XとYのデータ間の関係を表す数値で、0であれば、XとYは無相関ということを意味します。
そして、無相関であれば材料Aと材料Bを接合した後の寸法誤差は分散V(X)+V(Y)に従うということですね。
ですが、実際の製造現場では同じ鋼板のロールやロッドから切り出した部材や消耗した加工機などを使うので共分散が0でないことが多々ありそうですね。
ちなみに、ここでいう"XとYが無相関"と"XとYが独立"であることは異なる意味を持ちます。無相関とはあくまで、分散に注目してXとYの関係を評価しているだけなので、XとYの確率分布が独立であるとは限りません。