はじめに
みなさんは大槻班長をご存じでしょうか。
そうです、漫画カイジの地下強制労働施設で登場する悪党班長です。知らない人でも、カイジが生ビールを飲んだ際の名言「キンキンに冷えてやがるっ・・・!!」「犯罪的だ・・・うますぎる・・・」は聞いたことがあるのではないでしょうか。その生ビールをカイジにあげた人です。
実はこの大槻班長、一部のファンの間で大人気でスピンオフ漫画も出ています。
今回は大槻班長が地下強制労働施設でやっていたチンチロリンの不正を統計的に見破ることを目標に、2項分布の検定に取り組みます。
チンチロリンのルール(地下ver)
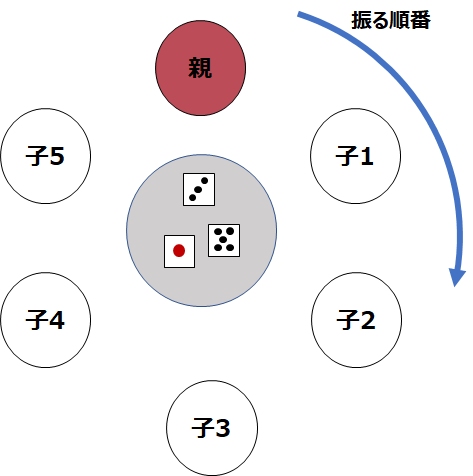
地下強制労働施設で行われていた賭博がチンチロリンです。そのルールはいたってシンプルで**サイコロ3つをどんぶりの中に投げ入れ、その出た役の強さで勝敗が決まります。**参加者は下図のように円形で座り、まず親が振り次に子たちが左回りに振り、親の目対子の目どっちが強いかでペリカ(地下労働施設の通貨で1円=10ペリカ)が行き来します。
だいたい下図のようなイメージです。
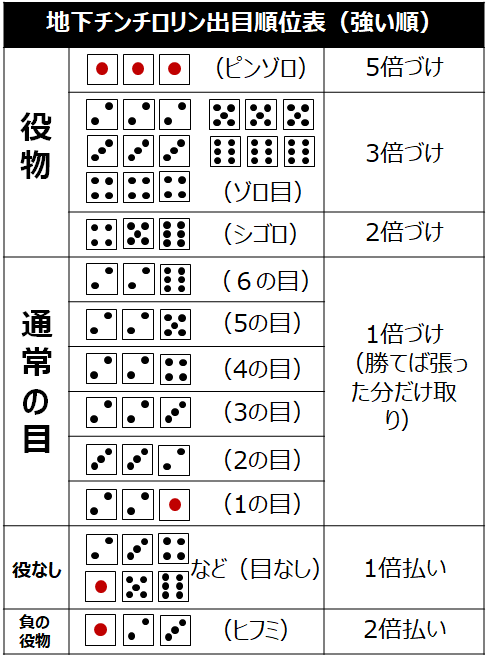
基本的には目の大きい方が強くて、ぞろ目やシゴロはその上の役といった感じになっています。
#ハンチョウのいかさまサイコロ
さて、ここでハンチョウが使ったイカサマサイコロを見てみましょう。いかさまサイコロには出目が4~6しかないのですが、同じ数字は真反対側に位置するように置かれているため、振られたサイコロを一見するだけではいかさまだと気づかれないようになっています。
さらにハンチョウはイカサマの露見を防ぐため、以下の2つの対策も取っています。
1、いつも使っていてはバレるから、1度の勝負で使うのは勝負所の2回だけ。
2、親番で使うときは子にも振らせるようにし、違和感を消す。
サイコロの出目で検定
推定統計を使って大槻班長のイカサマを見破る方法を検討していこうと思います。推定統計の検定は、事前に母集団に関して仮説をたてておいて、得られた標本が現実的な範囲に入ってるか確かめる手法です。
10人でプレイして1周親をまわすことを「1回の勝負」と仮定してます。
10日間毎日記録を取り続けた場合の結果(計回分のサイコロの目)を下に示しています。1度に3つのサイコロを振るのですが、簡単のために全て独立に考えています。なんとなく4~6が多く出てるのが分かります。
こういった、ある特定の分布(サイコロの場合は一様分布)に適合するかといった検定は適合度検定と呼ばれ、カイ二乗分布による検定を用いるのが一般的です。
ですが、今回は事前に4~6だけの目を持ついかさまサイコロを使っているらしいとの情報を得ていたと仮定して、以下のような検定を行うことにします。
各目が均等に出るサイコロであれば、振って4~6が出る確率は1/2であるはずですので、帰無仮説は「このサイコロを300回振ったときに4~6の目が出るのは半分の150回である」とします。
成功確率がpの試行をn回行ったときの成功回数は二項分布に従います。二項分布での成功回数(4~6がでる回数)の期待値はE(X)=npで、**分散はV(x)=np(1-p)**です。そして、二項分布を下記の式で標準化することで標準正規分布N(0, 1)に近似します。両側検定で棄却率を1%とすると、下記式のzが-2.68~2.68に入れば帰無仮説は正しいと考えます。
\begin{align}
z=\frac{X-np}{\sqrt{np(1-p)} \\}
\end{align}
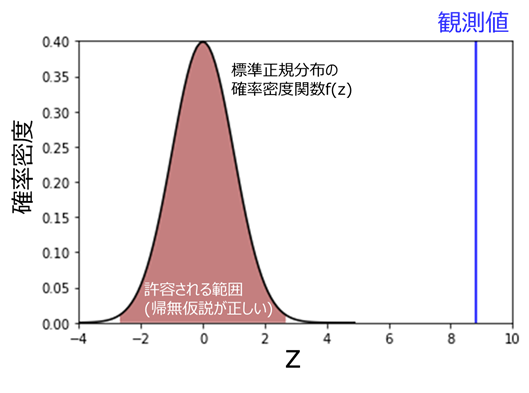
pythonのランダム関数でシミュレーションすると、以下の図のような結果が得られギリギリ棄却域には入りませんでした。

自分から見えるサイコロの3面の目の組み合わせで検定
次に、いかさまサイコロは4~6の値しか取らないため、「振られたサイコロの自分から見える3面の目×3つのサイコロの確率変数」を検定することを考えてみます。※角度によっては3面見えないときもある気がしますが、とりあえず進めます
自分から見えるサイコロの目の組み合わせは通常のサイコロ構造であれば、以下の8パターンのどれかになります。
(1,2,3)、(1,2,4)、(1,3,5)、(1,4,5)、(2,3,6)、(2,4,6)、(3,5,6)、(4,5,6)

そして、通常のサイコロでは見え方が(4,5,6)となる確率は1/8です。
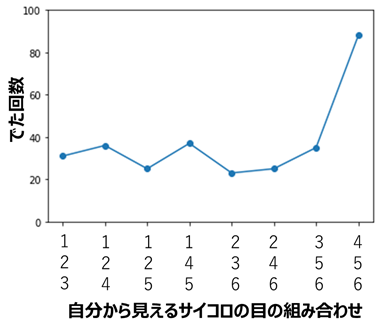
下図が観測された値です。当然ですが偏りがより顕著になりました。
そうすると、サイコロの出目だけで検定を行う場合よりも、より不正していることが確かだという結果がシミュレーションから得られました。
コード
import math
import random
import numpy as np
import matplotlib.pyplot as plt
#自分から見えるサイコロの目の見える目のパターン
look_pattern = {1:[1,2,3],
2:[1,2,4],
3:[1,3,5],
4:[1,4,5],
5:[2,3,6],
6:[2,4,6],
7:[3,5,6],
8:[4,5,6]}
counts_single = [0 for _ in range(7)]
counts_multi = [0 for _ in range(9)]
#10日間
for day in range(10):
#通常
for normal in range(8):
#3つのサイコロ
for dice_num in range(3):
#サイコロ見え方
result = random.randint(1,8)
counts_multi[result] += 1
#サイコロ出目
result = look_pattern[result][random.randint(0,2)]
counts_single[result] += 1
#イカサマ
for ikasama in range(2):
#3つのサイコロ
for dice_num in range(3):
#サイコロ見え方
result = 8
counts_multi[result] += 1
#サイコロ出目
result = look_pattern[result][random.randint(0,2)]
counts_single[result] += 1
#サイコロ出目
plt.scatter(range(len(counts_single[1:])),counts_single[1:])
plt.plot(range(len(counts_single[1:])),counts_single[1:])
plt.ylim(0,100)
plt.show()
#自分から見えるサイコロの目
plt.scatter(range(len(counts_multi[1:])),counts_multi[1:])
plt.plot(range(len(counts_multi[1:])),counts_multi[1:])
plt.ylim(0,100)
plt.show()
#検定
n = sum(counts_multi)
p = 1/8
X = counts_multi[8]
z = (X - n*p) / (n*p*(1-p))**0.5
ok_Xs = np.linspace(-2.68, 2.68, num = 50)
f = lambda x: (math.exp(-x**2/2)) / math.sqrt(2*math.pi)
plt.plot([i*0.1-5 for i in range(100)],[f(i*0.1-5) for i in range(100)], color = "black")
plt.fill_between(ok_Xs, np.zeros_like(ok_Xs),list(map(f, ok_Xs)),facecolor='darkred',alpha=0.5)
plt.plot([z,z],[0,1], color = "blue")
plt.ylim(0,0.4)
plt.xlim(-4,10)
plt.show()
参考
終わりに
最後まで読んで頂きありがとうございました。