OpenJij（量子アニーリング）を使って群れるロボを動かす

はじめに

この記事は筆者がHackDay2021に参加した際にチームでつくった「群れるロボットはかわいい」の技術説明 ~量子アニーリング手法について~ となります。(チーム名：VENT)

ロボット製作というよりは内部アルゴリズムの紹介となります。

[追記]
・HadkDay2021テクノロジー賞のJij賞を受賞しました！！！審査員の皆さま、スタッフの皆さま、そしてチームのみんな、本当にありがとうございました。副賞として頂いたjetson nanoも早く使ってみたいです!!

・全体システムとロボットの作り方についてチームメンバー（HackDay2021リーダー）がわかりやすく丁寧にまとめておりますので、そちらも是非ご覧ください。
→ [HackDay2021] 群れるかわいいロボットのつくり方

何をしたの？

YouTubeに動画を挙げています。（最近Qiitaに貼れるようになったんですね！）
90秒程度の動画なので是非みてみてください！。

群れるロボット..かわいくないですか？笑

ロボットの目的地設定 => 量子アニーリングで！

さて、ここからはロボットがどうやって目的地を決定しているのかを解説していきます。
今回はJij Inc.が提供するOpenJijを使わせていただきました。
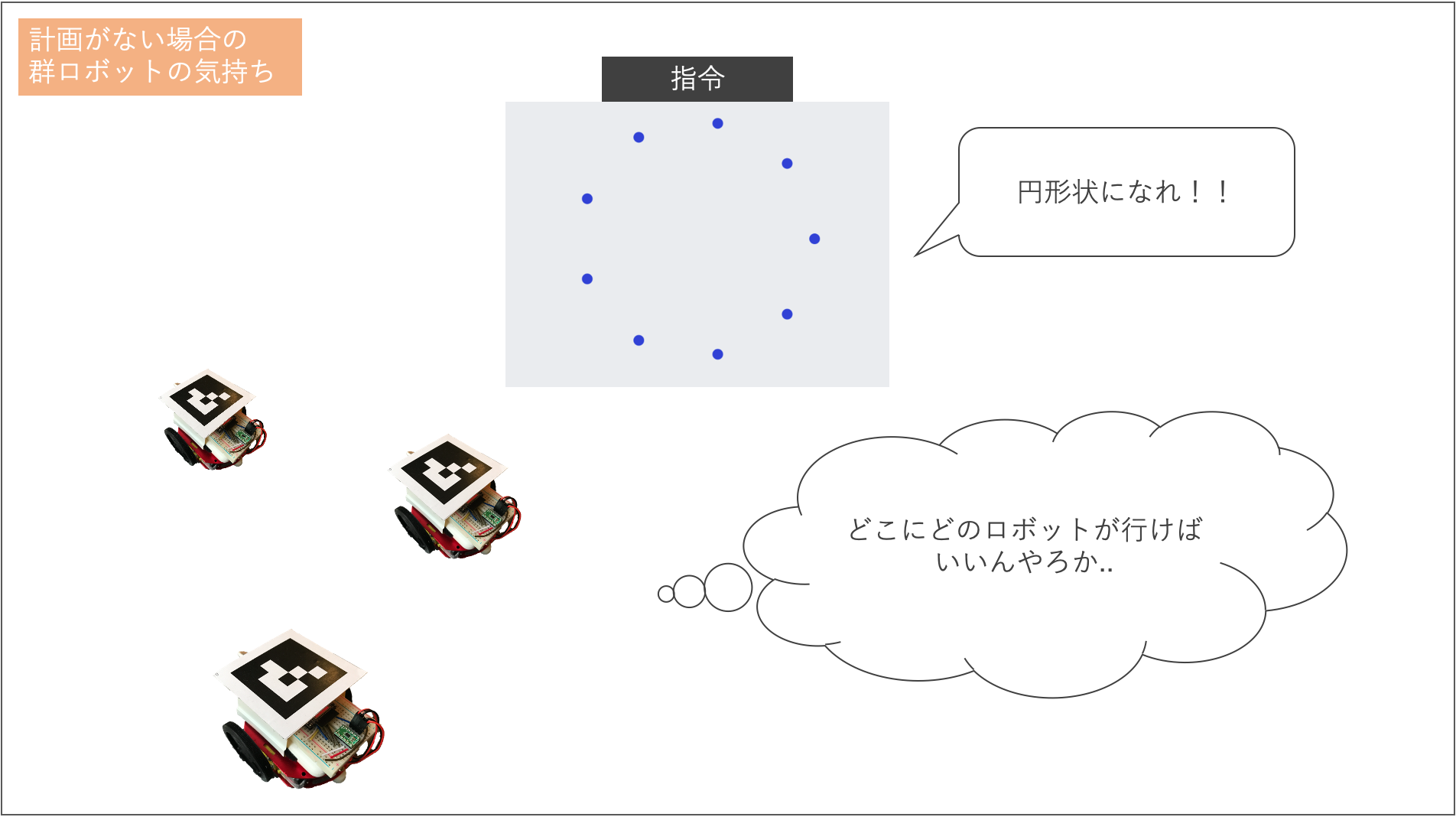
目的地を決定するアルゴリズムがないとロボットは下図のように途方に暮れてしまいます。

量子アニーリング手法とは？

一言でいうと、「組み合わせ問題に特化したヒューリスティックな最適化手法」ということです。高精度・高速度で一般には解くことが難しい（時間がかかる）問題にも適用できる、とのこと。

専門的な話を書き連ねるのはなかなか難しいですね。Wikipediaに簡単な概要がありますのでそちらを参照ください。

以下では、量子アニーリング手法を使えるOpenJijの導入と、問題設定を進めていきます。

OpenJijのインストール & チュートリアル

まずはpip installしましょう。
!pip install openjij

Jij社の方でチュートリアルも用意されております。こちらを確認すると様々な例題に当たれます。
今回ロボットをつくっていく上でも大変参考になりました。
リンク：OpenJijチュートリアル

問題設定とコーディング (本題)

ようやく本題です。
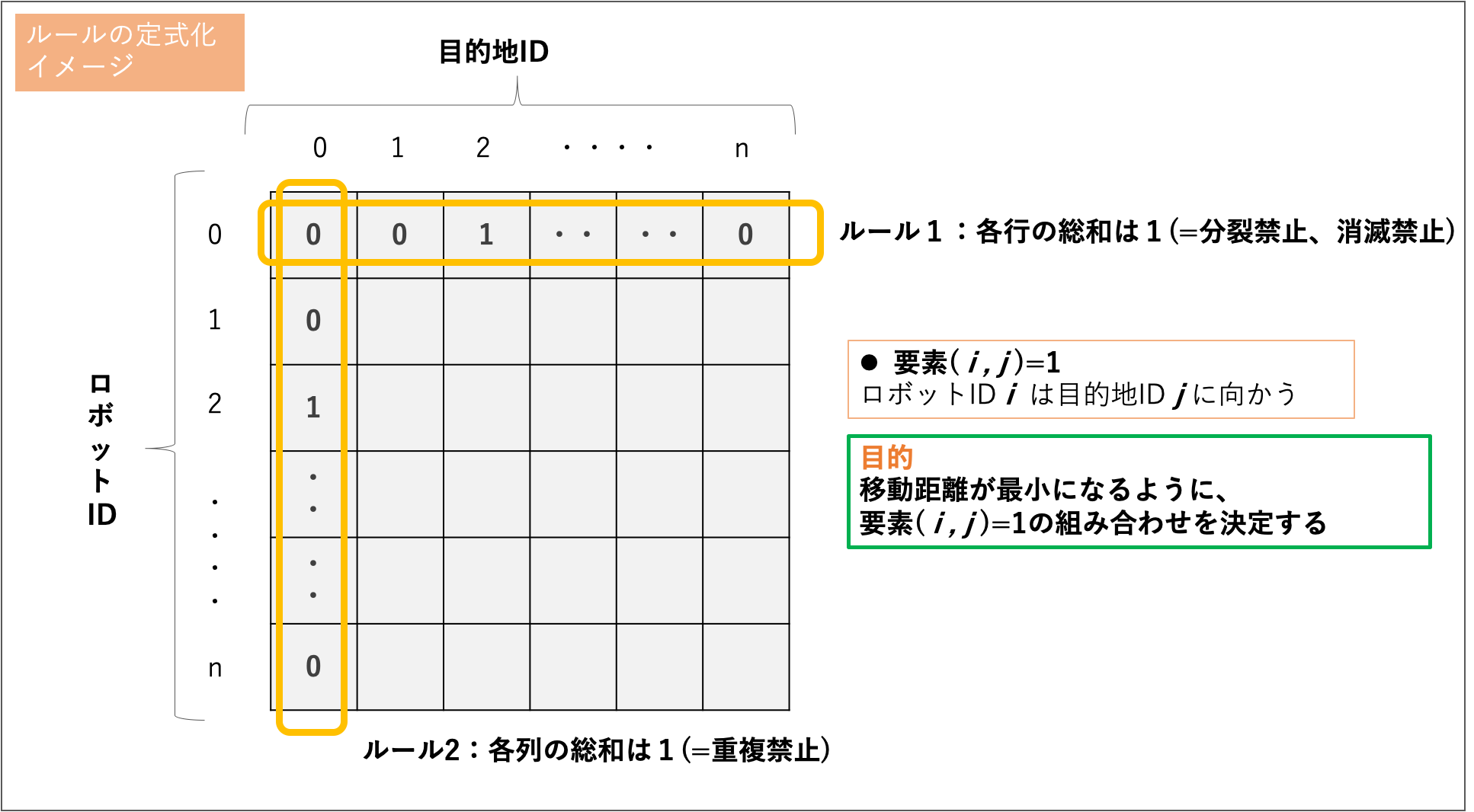
群ロボが効率よく行動していくにあたり、２つのルールと１つの目的があります。

【ルール】
その１：１つのロボットは複数目的地に到達できない (=分身できない、消滅できない）
その２：複数のロボットが１つの目的地に到達しては行けない (=重複しない)

【目的】
全体の移動距離総和が最小となる

上記のルールを満たすために、n×nの行列 (n:ロボット台数)を考えました。
定式化イメージは下図です。

プログラムコード

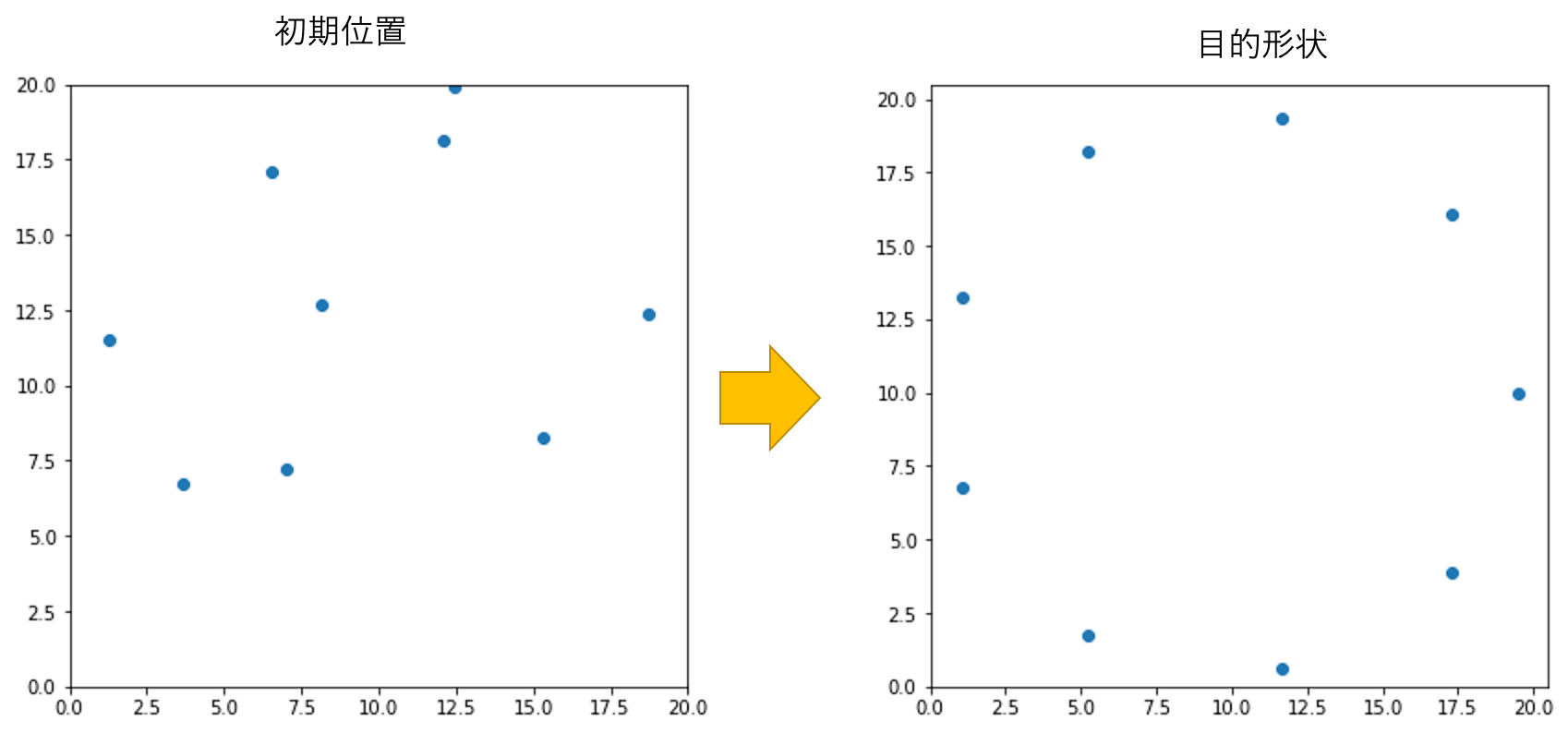
ここでは、ロボットの初期値と目的形状を適当に設定し、その後問題を解きます。
試しながらコーディングしているので美しくありませんがご容赦ください。

① ロボットの初期値＆目的地設定

import openjij as oj
import numpy as np
import pandas as pd
import random
import matplotlib.pyplot as plt

##ランダムに座標を振り分けるための関数
def init_xy(xylist,n,limit):
    LIMIT = limit
    i = 0
    while i < n:
        x = random.random()*LIMIT
        y = random.random()*LIMIT
        xylist[i]=[x,y]
        i += 1

n = 9 #ロボットの数
limit=20 # 平面の広さ。この場合は[0,0]->[20,20]まで値を取りうる
xylist = np.zeros((n,2))
init_xy(xylist,n,limit) ##適当に初期値を設定

##目的地は円
center = limit/2
r = limit/2-0.5
xylist_af = np.array([[center+r*np.cos(np.radians(i)),
                       center+r*np.sin(np.radians(i))] for i in range(0,360,int(360/n))])

これにより下図のような初期位置と目的形状が生成されます。

② openjijによる定式化

チュートリアルにある3-PyQUBO with OpenJijを参考にしました。

from pyqubo import Array, Constraint, solve_qubo
import neal

# node数 × node数の行列を作成する
x = Array.create('x', shape=(n,n), vartype='BINARY')

# 第一項 (制約項)を定義します。
#ルール１：あるnode(before)は１つのnode(after)に向かう=分裂禁止・消滅禁止
H_A1 = Constraint(sum((1-sum(x[v,i] for i in range(n)))**2 for v in range(n)), label='HA1')
#ルール２：あるnode(after)は１つのnode(before)から選ばれる=重複禁止
H_A2 = Constraint(sum((1-sum(x[i,v] for i in range(n)))**2 for v in range(n)), label='HA2')

# 第二項 (コスト、目的関数)を定義します。
H_B = sum((x[v,i]*np.linalg.norm(xylist[v]-xylist_af[i])) for i in range(n) for v in range(n))

## ハミルトニアン全体を定義します。
# ここの係数の重み付けは結果に影響与える
Q = 12*H_A1+12*H_A2+H_B

# モデルをコンパイルします。
model = Q.compile()
qubo, offset = model.to_qubo()


# nealのSAを用いて解きます。
sampler = neal.SimulatedAnnealingSampler()
raw_solution = sampler.sample_qubo(qubo)
print(raw_solution)

# 得られた結果をデコードします。
decoded_sample = model.decode_sample(raw_solution.first.sample, vartype="BINARY")
# さらに解を見やすくする処理を追加します。
# .array(変数名, 要素番号)で希望する要素の値を抽出することができます。
x_solution = {}
to_list = []
for i in range(n):#(n):
    x_solution[i] = {}
    for j in range(n):
        x_solution[i][j] = decoded_sample.array('x', (i, j))
        if decoded_sample.array('x', (i, j))==1:
            to_list.append(j)
print(raw_solution.first.energy)

これで最適結果の取得は完了です。
ここでのポイントはハミルトニアン(Q)の定義式ですね。係数を変えると計算結果に大きな影響を与えます。制約項の係数が大きすぎてもダメなようで、ここに量子アニーリング手法の不思議さを感じます。

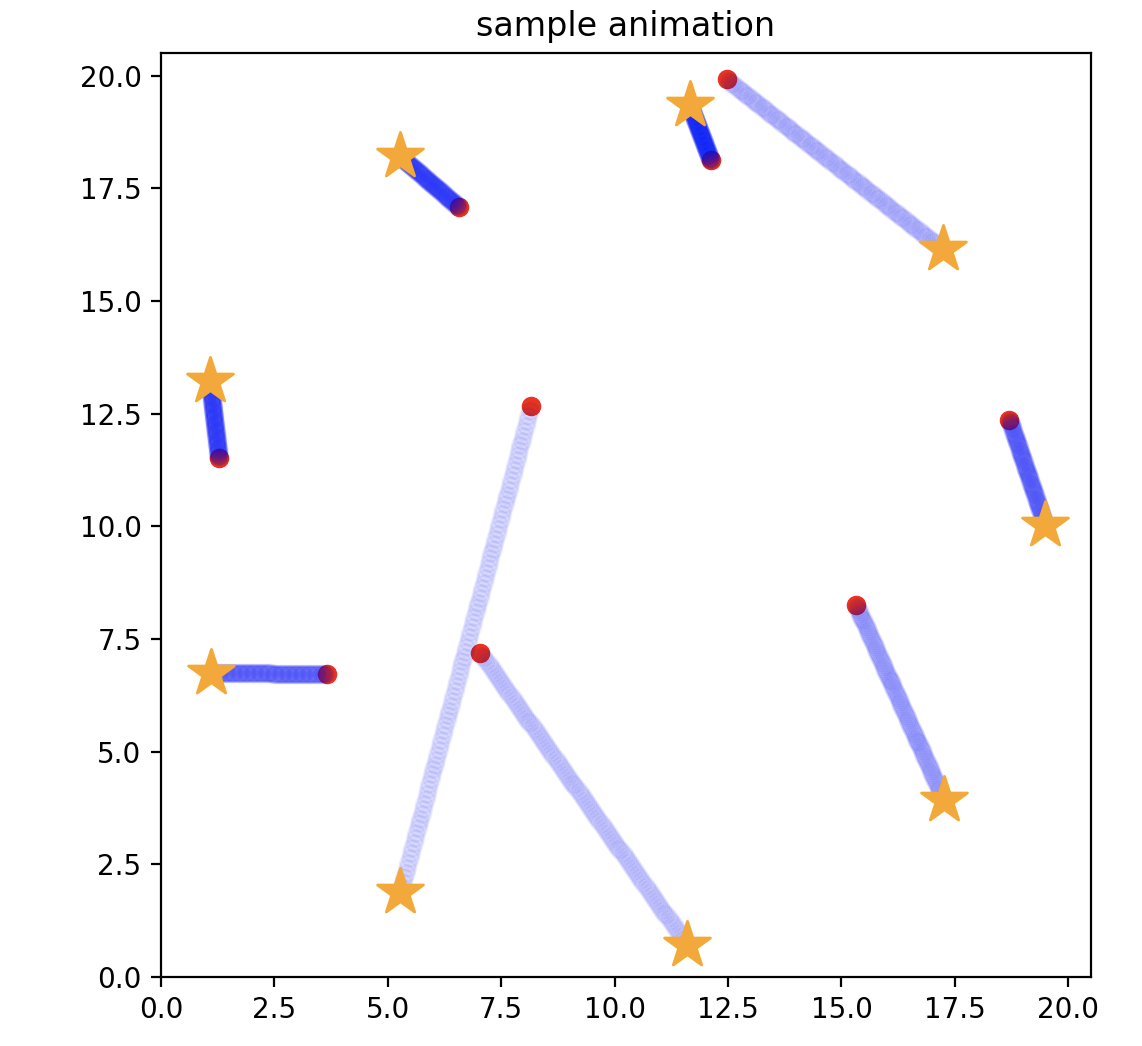
結果

いい感じですね！！赤丸が初期値を、星が目的地を示しています。ちゃんと移動距離の総和が最小になるように動いていますね。

可視化コードはこんな感じです。↓

%matplotlib notebook
from matplotlib import animation

fig = plt.figure()
ims = []

STEP = 100

#向かう先のベクトル取得
vec = (xylist_af[to_list] -xylist)/STEP

plt.figure(figsize=(6, 6))
for i in range(STEP):
#     rand = np.random.randn(100) # 100個の乱数を作成
    if i == 0:
        img = plt.scatter(xlist,ylist,color='red') # グラフを作成
        plt.title("sample animation")
        plt.ylim(0,limit+0.5)
        plt.xlim(0,limit+0.5)

        xlistnow = xlist
        ylistnow = ylist

    else:
        xlistnow = xlistnow + vec[:,0]
        ylistnow = ylistnow + vec[:,1]

        img = plt.scatter(xlistnow,ylistnow,color='blue',alpha=0.05)

    ims.append(img) # グラフを配列に追加

img = plt.scatter(xlistnow,ylistnow,s=300, c="orange", marker="*")
ims.append(img)

# 100枚のプロットを 100ms ごとに表示するアニメーション
ani = animation.ArtistAnimation(fig, ims, interval=100)

plt.show()

さいごに

24時間ハッカソン楽しかった！けどしんどかった。
おそらく近いうちにgithub repositoryを公開する..のかな。