機械学習
第1章 線形回帰モデル
要約
線形回帰モデルは回帰問題を解くための機械学習モデルの一つである.その特徴は,教師あり学習で,入力とパラメータの線形結合を出力するところである.
入力を$\boldsymbol x$,パラメータを$\boldsymbol w$,予測値を$\hat y$とし,$\boldsymbol x$,$\boldsymbol w$を以下のように書くとする.
\boldsymbol w=
\begin{pmatrix}
\boldsymbol{w_1} & \boldsymbol{w_2} & ... \\
\end{pmatrix}^T\quad
\boldsymbol x=
\begin{pmatrix}
\boldsymbol{x_1} & \boldsymbol{x_2} & ... \\
\end{pmatrix}^T
このとき,予測値$\hat y$は入力とパラメータの線形結合で次式のように書ける.
$$\hat y=\boldsymbol w^T \boldsymbol x+w_0=\sum_{j=1}^{m}w_jx_j+w_0$$
パラメータ$\boldsymbol w$は最小二乗法により推定する.
データは学習用データと検証用データに分割する.モデルの能力は汎化性能(generalization),つまり未知のデータに対するモデルの精度によって決まるため,学習用データを用いて作ったモデルが検証用データに対してどれだけの汎化性能があるかが重要である.
パラメータの推定を行う.学習データ$y_i^{(\mathrm {train})}$と予測値$\hat y_i^{(\mathrm {train})}$の最小二乗誤差(mean squared error : MSE)は次式となる.
$$\mathrm{MSE_{train}}=\frac{1}{n_{train}}\sum_{i=1}^{n_{train}}(\hat y_i^{(\mathrm {train})}-y_i^{(\mathrm {train})})^2$$
MSEを最小にするような$\boldsymbol w$を$\hat{\boldsymbol w}$とおく.次式が成立する$\boldsymbol w$を求める.
$$\frac{\partial}{\partial{\boldsymbol w}}\mathrm{MSE_{train}}=0$$
この結果,次式を得る.
$$\hat{\boldsymbol w}=(X^{(train)T}X^{(train)})^{-1}X^{(train)T}\boldsymbol y^{(train)}$$
予測値は次式となる.
$$\hat{\boldsymbol y}=X\hat{\boldsymbol w}=X(X^{(train)T}X^{(train)})^{-1}X^{(train)T}\boldsymbol y^{(train)}$$
実装演習
ボストンの住宅データセットを用いて線形回帰の演習を行う.
課題:部屋数4,犯罪率0.3の住宅価格を予測する.
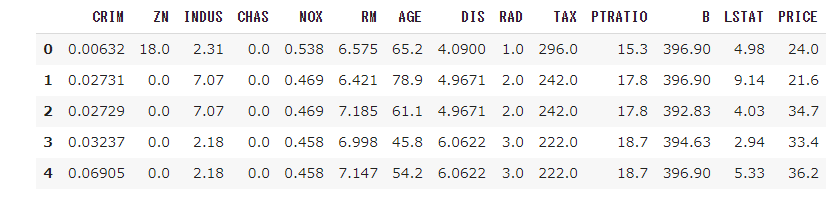
データフレームは以下である.
部屋数はRM,犯罪率はCRIM,住宅価格はPRICEである.
まず,線形単回帰分析で住宅価格を予測した.入力をRMとする.以下のモデルが得られた.
回帰係数:9.102
切片:-34.671
回帰係数が正なので,部屋数が増えるほど住宅価格が上がることが分かる.
次に,線形重回帰分析で住宅価格を予測した.入力をCRIM, RMの2変数とする.以下のモデルが得られた.
回帰係数:(CRIM, RM)=(-0.26491325, 8.39106825)
切片:-29.24471945192992
犯罪率が高いと住宅価格は下がり,部屋数が多いと住宅価格は上がることが分かる.
第2章 非線形回帰モデル
要約
非線形回帰モデルでは基底展開法を用いる.入力$\boldsymbol x$を一度写像して線形結合をすることで$y_i$を予測する.
$$y_i=f(\boldsymbol x_i)+\epsilon_i $$
$$f(\boldsymbol x_i)=w_0+\sum_{i=1}^{m}w_j\phi_j(\boldsymbol x_i)$$
非線形回帰の1次元の基底関数の例を挙げる.
・多項式
$$\phi_j=x^j$$
$j=1$のときは線形結合となる.
・ガウス型基底
$$\phi_j(x)=\exp{\Big\{ \frac{(x-\mu_j)^2}{2h_j} \Big\}}$$
未学習(underfitting)と過学習(overfitting)に対する対策を示す.
未学習の場合の対策
・表現力の高いモデルを利用する.
過学習の場合の対策:
・学習データの数を増やす.
・不要な基底関数を削除する.
・正則化法を利用する.
過学習に対する正則化法を説明する.
$$S_\gamma=(\boldsymbol y-\Phi\boldsymbol w)^T(\boldsymbol y-\Phi\boldsymbol w)+\gamma R(\boldsymbol w) \quad(\gamma>0)$$
ここで,$\gamma R(\boldsymbol w)$が正則化項となる.$\gamma$はパラメータである.
正則化項として,L1ノルムおよびL2ノルムを使う方法がある.
| 推定量の名称 | 利用するノルム | 特徴 |
|---|---|---|
| Ridge推定量 | L2ノルム | パラメータを0に近づけるよう推定 |
| Lasso推定量 | L1ノルム | いくつかのパラメータを正確に0に推定 |
続いて,モデル精度の検証法について述べる.
交差検証法は適切なモデルを決定する方法である.データを学習用と評価用に分割する.例えば,5分割の場合,検証データと学習データの組み合わせによって検証モデルは5つできる.各モデルの精度の平均値(CV値)をモデル精度とする.
第3章 ロジスティック回帰モデル
要約
ロジスティック回帰モデルはベルヌーイ分布に従う変数の統計的回帰モデルの一種である.ここでは,ロジスティック回帰モデルを用いて分類問題を扱う.分類問題ではシグモイド関数がよく用いられる.理由はシグモイド関数の微分がそれ自身で表現でき,尤度関数を微分する際に計算が容易になるからである.以下にシグモイド関数とその微分を示す.
$$\sigma =\frac{1}{1+e^{-1x}}$$
$$\frac{\partial \sigma(x)}{\partial x}=a\sigma(x)(1-\sigma(x))$$
分類問題を扱うため,シグモイド関数の出力を$Y=1$になる確率に対応させる.説明変数の実現が与えられたとき,$Y=1$になる確率は次のように表せられる.
$$P(Y=1|\boldsymbol x)=\sigma(w_0+w_1x_1+\cdots+w_mx_m)$$
この確率が0.5以上ならば$Y=1$,0.5未満ならば$Y=0$と予測する.
次に$Y=0$と$Y=1$になる確率をまとめて表現する.ベルヌーイ分布は確率$p$で$1$,確率$1-p$で$0$をとる離散確率分布を表す.
$$P(y)=p^y(1-p)^{1-y}$$
最尤推定法にしたがって,パラメータ$\boldsymbol w$を求める.尤度関数は次式となる.
$$P(y_1,y_2,\cdots,y_n|w_0,w_1,\cdots,w_m)=\prod_{i=1}^n p_i^{y_i}(1-p_i)^{1-y_i}=L(\boldsymbol w)$$
これらを次式に置き換える.
$$E(w_0,w_1,\cdots,w_m)=-\log L(w_0,w_1,\cdots,w_m)$$
対数尤度関数$E(\boldsymbol w)$を最小化するパラメータ$\boldsymbol w$を探査する.
実装演習
タイタニックの乗客データを用いて,年齢が30歳の男性の乗客は生き残れるかどうかを分類する.
まず,今回のデータ分析に必要のない列は削除する.

以下のようにデータを削減した.
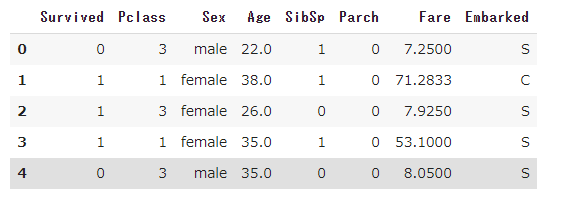
次にAgeカラムの欠損値を中央値で補間した.
実際にロジスティック回帰を行っていく.ここでは,チケット価格から生死を判別する.パラメータ探査後,以下のように例えば,61歳は死亡という予測ができ,またその確率も示すことができた.
model.predict([[61]])
実行結果
array([0])
model.predict([[61]])
実行結果
array([[0.50358033, 0.49641967]])
上の例だと,確率を考慮すれば,生還と死亡の確率はどちらも0.5程度であるということも分かる.
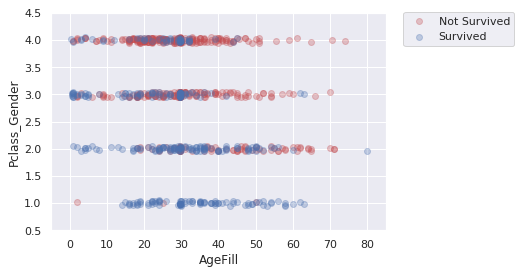
また,説明変数を組み合わせることで,新たな視点でデータを分析できる.下の図は,縦軸がPClass+Genderとしている.これは階級が高く,かつ女性であるほど生還するという仮説に基づく変数であり,値が小さいほど,生還しやすいという仮説がある.横軸は年齢であり,年齢が低いほど生還するという仮説がある.分析の結果は,仮説通り,図中の点が左下に向かうほど,生還数が多いことが分かる.
第4章 主成分分析
要約
主成分分析とは多変量データの持つ構造を情報の損失をなるべく小さくしつつ,少数変数に次元を圧縮する分析である.
$m$次元のデータが以下のようにあるとする.
$$\boldsymbol x_i=(x_{i1},x_{i2},\cdots,x_{im})\in \mathbb{R} $$
これの次元を圧縮するために以下のように線形変換を行う.
$$\boldsymbol s_j=(s_{1j},\cdots,s_{nj})^T=\bar X\boldsymbol a_j$$
ここで$\bar X$は中心化したデータ行列,$\boldsymbol a_j$は$m$次元のパラメータである.
情報の量を分散の大きさと考えると,線形変換後の分散が最大となるように射影軸をとればよいことになる.
$$\mathrm{Var}(\boldsymbol s_j)=\boldsymbol a_j^T\mathrm{Var}(\bar X)\boldsymbol a_j$$
これを最大化する$\boldsymbol a_j$を探査するわけだが,解が無限に表れるのを防ぐため,ノルムを$1$とする制約を与える.
結局,制約つき最適化問題を解くことになるので,次式のラグランジュ関数を最大化する係数ベクトルを探査すればよい.
$$E(\boldsymbol a_j)=\boldsymbol a_j^T\mathrm{Var}(\bar X)\boldsymbol a_j-\lambda(\boldsymbol a_j^T\boldsymbol a_j-1)$$
実際に$\boldsymbol a_j$についての$E(\boldsymbol a_j)$の微分が0になるように計算すると次式を得る.
$$\mathrm{Var}(\bar X)\boldsymbol a_j=\lambda \boldsymbol a_j$$
結局,元データの分散共分散行列$\mathrm{Var}(\bar X)\boldsymbol a_j$の固有ベクトルを求めることになる.
情報の損失率を調べるために累積寄与率を導入する.累積寄与率は第1主成分から第$k$主成分まで圧縮したときの情報損失量の割合であり,次式で表すことができる.
$$r_k=\frac{\sum_{j=1}^k \lambda_j}{\sum_{j=1}^m \lambda_j}\quad (1\le k\le m)$$
実装演習
乳癌検査データから良性か悪性かを分類する.32次元のデータを2次元に次元圧縮したとき,分類が可能かを確認する.
ここで,元のデータを用いてロジスティック分析を行うと,検証スコア97%で分類できることを確認できている.
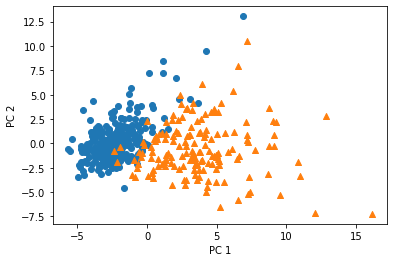
主成分分析の結果は以下のグラフのようになった.今回は2次元にまでデータを圧縮してみて,分類可能か確認する.
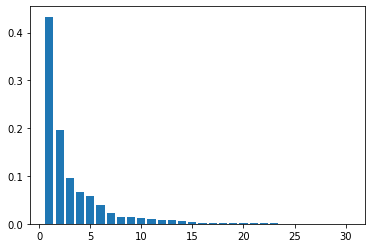
すると以下のグラフのような結果になる.縦軸が第2主成分,横軸が第1主成分,マーキングは〇が良性,△が悪性である.ある程度の分類は可能であるが,元のデータで検証スコア97%であることを考えると,決定境界線はより不明瞭になり,精度が低下していると判断できる.
第5章 アルゴリズム
k近傍法(kNN)
要約
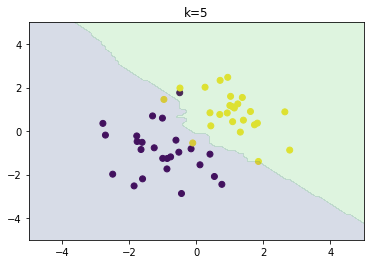
分類問題の機械学習手法である.あるデータ1つのクラスを分類するとき,そのデータの最近傍のデータ$k$個が最も多く所属するクラスを選ぶ.故に$k$を変化させると結果も変化する.$k$が大きいほど決定境界は滑らかになる.
実装演習
以下のようなランダムなデータにk近傍法を適用し,分類を行う.
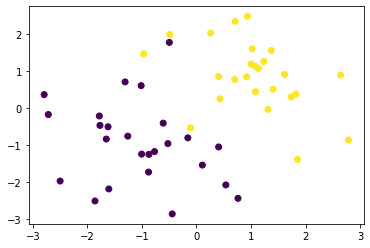
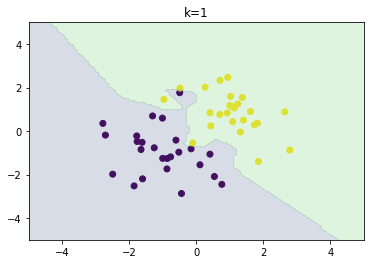
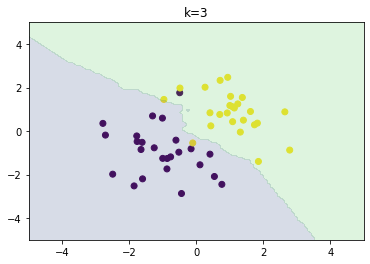
以下のグラフはそれぞれ$k=1,3,5$の場合の分類結果である.$k$が大きいほど決定境界が滑らかになることを確認できた.
k-平均法(k-means)
要約
教師なし学習でのクラスタリング手法である.データを$k$個のクラスタに分類する.各クラスの中心の場所を任意に決めて,各データは自身と中心との距離が最も近いクラスに属する.ここで,クラスタリング結果は中心の初期値に依存するため,初期値の決め方は重要である.そのような方法には例えばk-means++などがある.
実装演習
以下のようなランダムなデータにk近傍法を適用し,クラスタリングを行う.
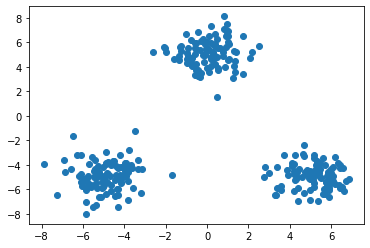
k-meansアルゴリズムは以下のとおりである.
- 各クラスタ中心の初期値を設定する
- 各データ点に対して、各クラスタ中心との距離を計算し、最も距離が近いクラスタを割り当てる
- 各クラスタの平均ベクトル(中心)を計算する
- 収束するまで2, 3の処理を繰り返す
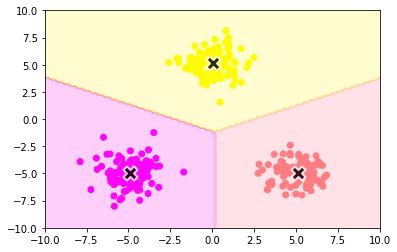
実行の結果,以下の図のようにデータを3つのクラスターに分類することができた.
第6章
※第6章はレポート対象範囲外
第7章 サポートベクターマシーン
要約
サポートベクターマシン(support vector machine, SVM)は2クラス分類における決定境界を与える手法である.決定境界は以下のようにマージン$\kappa$を用いて以下のような条件を与える.
$$|\boldsymbol w^T\boldsymbol x+b|\ge \kappa$$
また,データを線形分離できないときは,誤差を許容し,誤差に対してペナルティを与える.この手法はソフトマージンSVMと呼ばれる.