Eigenを用いた密行列演算・分解の概要

この記事では、私が普段よく利用している行列演算ライブラリ Eigen から密行列関連の機能を簡単に紹介します。
詳細が気になる方は Eigen ホームページ http://eigen.tuxfamily.org （英語）をご覧ください。
開発環境としては、Visual Studio か GCC を想定しており、簡単なプログラムの実装とコンパイルができることを想定しています。
また、執筆時点でのEigen のバージョンは 3.3.4 です。（2019/5/1追記：今はバージョン 3.3.7 が出ていますが、ここに書いている内容が変わるほどの変更はないようです。）
なお、Matlab が使える人向けのコメントを所々に書いています。

加筆・訂正して欲しい部分がありましたら教えてください。

環境

Eigen は全てがヘッダファイルに書かれているため、基本的に対応するコンパイラがあれば動きます。（対応するコンパイラについてはホームページを参照。）
私が使ったことのある環境は次のものです。

• Windows 8.1, Visual Studio 2015/2017
• Windows 10, Visual Studio 2017/2019
• Windows 8.1, Mingw, GCC 6.3.0
• Windows 8.1, msys2, mingw-w64-x86_64-toolchain, GCC 7.2.0
• Ubuntu 16.04, GCC 7.2.0

準備

ここでは、ダウンロードして使う方法を紹介しておきます。
まず、Eigen のホームページ http://eigen.tuxfamily.org に行って右側の Get it の中にある tar か zip をダウンロードして展開します。展開してできたフォルダ（2018/1/7現在だとeigen-eigen-5a0156e40febというフォルダ）の中に Eigen というフォルダがあり、その中にヘッダファイルが大量に詰まっています。zip を展開したフォルダの中には、他にも bench とか test とかいうフォルダが入っていますが、使いません。
続いて、tar や zip を展開してできるフォルダをインクルードディレクトリに追加します（後述）。あとは、#include <Eigen/Core> のようにヘッダを読み込めば使えます。

Visual Studio の場合

Visual Studio で Eigen を使う場合は、プロジェクトを右クリックしてプロパティを選ぶと出てくるダイアログボックスの中から、

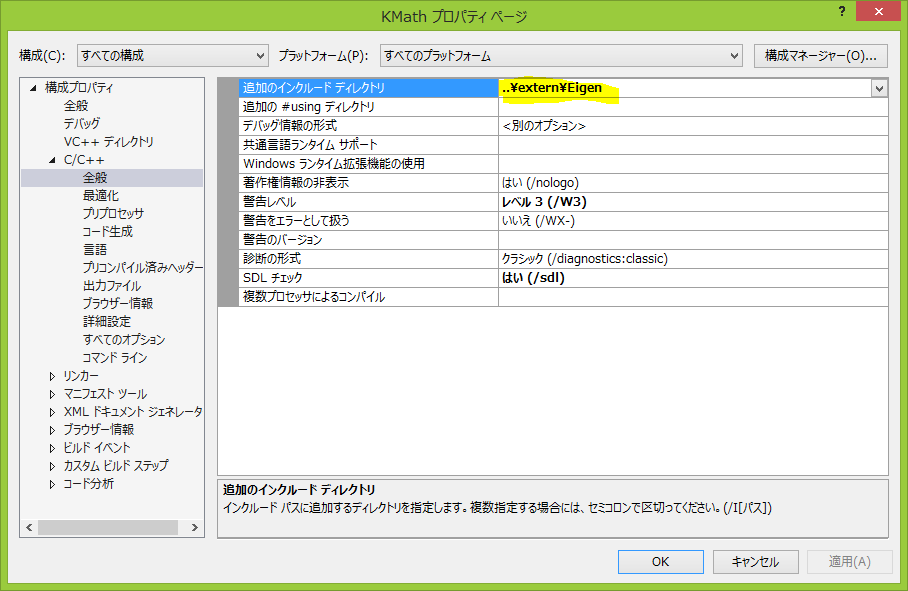
この画像のように追加のインクルードディレクトリへ zip を展開してできるフォルダへのパスを追加します。
ついでに、OpenMP を有効にしたりベクトル化演算（SSEとかAVX）を有効にしたりしておくと自動でスピードを上げてくれます。

• OpenMP の設定：構成プロパティ -> C/C++ -> 言語 -> OpenMP のサポート
• ベクトル化の設定：構成プロパティ -> C/C++ -> コード生成 -> 拡張命令セットを有効にする

GCC の場合

コンパイル時に

g++ source.cpp -I path_to_eigen
g++ source.cpp -isystem path_to_eigen

のように tar を展開してできるフォルダへのパスを -I や -isystem で追加します。-isystem の方が Eigen のコードに対する大量の warning を防げるのでお勧めです。（毎回打つのは面倒ですのでパスを環境変数に書いたり Makefile を使ったりしましょう。）
OpenMP （-fopenmp）を有効にしたりベクトル化演算（-sse、-mavx とか）を有効にしたりしておくと自動でスピードを上げてくれます。

行列のクラスと基本操作

まず、基礎的な（密）行列とそれの基本的な操作を紹介します。
Matlab を使っている方は Eigen のドキュメントにある
http://eigen.tuxfamily.org/dox/AsciiQuickReference.txt
をご覧ください。

行列の定義

Eigen::Matrix というテンプレートクラスが行列を定義しています。
サイズが小さい行列については Eigen::Matrix<Type, rows, columns> のように要素の型と行数・列数を指定して使います。例えば、double の 3 x 4 行列 mat は Eigen::Matrix<double, 3, 4> mat; で定義します。
また、サイズが小さくない行列については、動的に行数や列数を決める Eigen::Dynamic を使います。例えば、int の3列の行列 mat は Eigen::Matrix<double, Eigen::Dynamic, 3> mat; とします。
さらに、基本的な行列については typedef が用意されており、例えば

Eigen::Matrix3i = Eigen::Matrix<int, 3, 3>
Eigen::Matrix2f = Eigen::Matrix<float, 2, 2>
Eigen::MatrixXd = Eigen::Matrix<double, Eigen::Dynamic, Eigen::Dynamic>

のように Matrix の後にサイズと型の頭文字が並ぶようなものが定義されています。X は動的に決めることを表します。

ちなみに、Eigen のドキュメントによると、要素数が32くらいを超えるなら行数・列数を動的に（Eigen::Dynamic）するのが良いそうです。（ http://eigen.tuxfamily.org/dox/group__TutorialMatrixClass.html#TutorialMatrixTypedefs ）
基本的には Eigen::MatrixXd を使うことが多いと思います。

ベクトルの定義

ベクトルは行数または列数が1の行列として定義します。これに対しても

Eigen::Vector3d = Eigen::Matrix<double, 3, 1>
Eigen::RowVector2f = Eigen::Matrix<float, 1, 2>
Eigen::VectorXd = Eigen::Matrix<double, Eigen::Dynamic, 1>

のような typedef があります。基本的には Eigen::VectorXd を使うことが多いと思います。

要素へのアクセス

行列 mat を作ったら、mat(row_index, column_index) のように要素へアクセスします。
例えば2行目1列目は mat(2, 1) です。
行や列が欲しい場合は mat.row(2) とか mat.col(1) とか書きます。
ブロック行列を取り出すには mat.block(row_begin, col_begin, rows, cols) のように行と列の最初のインデックスと取り出す行数・列数を指定する基本的なものから、mat.rightCols(rows)、mat.topLeftCorner(rows, cols) のように端の要素を取り出すものまで色々とあります。

ベクトル vec については vec(2) のように1要素へアクセスする機能がある他、vec.segment(index_begin, elements) のように指定したインデックスから指定した個数の要素を取り出す機能があります。

全てを挙げると記事が非常に長くなりそうですので、詳しくはまたの機会に…。

初期化

行列やベクトルを Eigen::MatrixXd mat; のようにただ定義しただけだと、初期状態の要素は決まっていません。（EIGEN_INITIALIZE_MATRICES_BY_ZERO というプリプロセッサで必ず0で埋めるようにすることもできます。）
ここでは初期化の仕方を紹介します。行列のタイプを MatType としたとき、

• すべて0で埋める：MatType mat = MatType::Zero(rows, cols)
• すべて1で埋める：MatType mat = MatType::Ones(rows, cols)
• 単位行列にする：MatType mat = MatType::Identity(rows, cols)
• 乱数で埋める：MatType mat = MatType::Random(rows, cols)

のように初期化できます。また、mat.setZero() のようにメンバ関数で要素を埋めることもできます。

基本演算

計算したい行列ができたら、さっそく演算をしていきましょう。
mat は行列かベクトル、scalar はただの数字（doubleとか）とすると、

• 和：mat1 + mat2
• 差：mat1 - mat2
• 積：mat1 * mat2、mat * scalar
• 商：mat / scalar （行列による除算は後程…）

のように基本的な行列の演算は見た目通りの式を書くだけです。これらを組み合わせて mat1 = (mat2 + mat3) * mat4 のようにプログラムを書いていくことで計算できます。
さらに、演算した結果を代入する mat1 *= mat2、mat /= scalar のような演算子も定義されています。

行列としての積ではなく、単に要素ごとで掛け算や割り算がしたいときは

mat1 = mat2.array() * mat3.array() / mat4.array()

のようにします。（Matlab の .* と ./。）この array() メンバー関数の返り値を用いると、要素ごとの様々な計算ができます。例えば、各要素で sin(x1) + pow(x2, x3) を計算するには sin(mat1.array()) + pow(mat2.array(), mat3.array()) とします。
全要素の和を取る mat.sum() や最大値を取る mat.maxCoeff() なども便利です。

これらについても様々な演算がありますので、全てを載せるのはまた別の機会にします。

行列の分解

行列の和と差と積は簡単ですが、商は一般に行列の分解を用いた比較的重い演算を要します。また、固有値分解や特異値分解など、数値計算にしばしば必要な分解もあります。ここでは、そのような行列の分解について説明していきます。
ドキュメント上の一覧はこちら↓
http://eigen.tuxfamily.org/dox/group__TopicLinearAlgebraDecompositions.html

LU分解

まず最初に一般の正方行列の逆行列に使える LU 分解のクラスです。
PartialPivLU と FullPivLU の2つがあり、後者の方がより時間をかけて精度よく解くものとなっています。例えば、double の A x = b が解きたいならば

Eigen::PartialPivLU<Eigen::MatrixXd> lu(A);
x = lu.solve(b);

Eigen::PartialPivLU<Eigen::MatrixXd> lu;
lu.compute(A);
x = lu.solve(b);

のようにします。テンプレートパラメータで行列のタイプを指定し、コンストラクタや compute() メンバ関数で係数行列を渡すと内部で行列分解をしてくれて、solve() メンバ関数で解きたい右辺のベクトル（行列）を渡すと解が返ってきます。

Cholesky 分解

係数行列が実対称行列、または自己随伴行列で、正定値であることが分かっている場合、LLT か LDLT を使うと比較的軽く解を得られます。後者の方が時間をかけて精度よく解くものとなっています。使い方は LU 分解と同じです。

QR 分解

最小二乗法により、長方形の係数行列をもつ方程式 A x = b を解く場合は QR 分解を用います。使い方は LU 分解と同じで、HouseholderQR、ColPivHouseholderQR、FullPivHouseholderQR の3種類があります。後者ほど時間をかけて精度よく解くものになります。
係数行列が列の数と同じランクを持っていないような A x = b を解く際は特異値分解を用いてください。

固有値分解

固有値分解は EigenSolver、ComplexEigenSolver、SelfAdjointEigenSolver のようなクラスでできます。それぞれ実数の行列、複素数の行列、実対称or自己随伴行列を解くもので、コンストラクタや compute() メンバ関数で分解を計算します。その結果は eigenvalues()（固有値のベクトル）や eigenvectors()（固有ベクトルを並べた行列）で得られます。
さらに、一般化特異値分解をする GeneralizedEigenSolver、GeneralizedSelfAdjointEigenSolver もあります。

特異値分解

特異値分解は JacobiSVD と BDCSVD でできます。前者の方が正確ですが、行列のサイズが増えると非常に遅くなるため、BDCSVD を使うのがお勧めです。これらもコンストラクタや compute() で分解し、次のメンバ関数で結果を取り出します。

• 特異値：singularValues()
• 左特異ベクトルを並べた行列：matrixU()
• 右特異ベクトルを並べた行列：matrixV()
• 方程式を解く：solve()

なお、特異値以外を利用する場合は、コンストラクタや compute() の第2引数でそれを指定する必要があります。その引数としては、ComputeThinU、ComputeFullU、ComputeThinV、ComputeFullV があり、full のときは各行列が正方行列になりますが、thin のときは線形方程式を解くのに必要最低限のサイズの行列のみが計算されます。
これを用いると、行列の形やランクに依らず Moore-Penrose の一般化逆行列による A x = b の解が求められます。

注意点

ここでは、私が Eigen を使っていて困ったことを紹介します。

インデックスの型

Eigen と標準ライブラリを一緒に使う際にたまに困るのが、インデックスの型です。
標準ライブラリは符号なしの std::size_t を使うのに対し、Eigen は符号付きの std::ptrdiff_t を Index として定義し使っています。そのため、しっかりと warning を出す設定でコンパイルをするには適宜キャストが必要です。

auto の使用

参考：http://eigen.tuxfamily.org/dox/TopicPitfalls.html

コンテナを扱う際などに重宝する auto が Eigen では期待通りに動かない場合がありますので、それについてここで説明します。
Eigen では演算の結果として表現テンプレートと呼ばれるテンプレートクラスのオブジェクトを返し、それを行列へ代入する際に演算を行います。例えば、mat1 + mat2 は mat1 と mat2 の和を表すような表現を返しており、それを行列に代入するとき初めて和が計算されます。
そのため、結果を auto で受け取ると、演算結果でなく演算を表す内部的なオブジェクトを受け取ることになってしまいます。Eigen の演算結果を扱う際は auto を使わないようにしましょう。（自分が何をしているのか分かって敢えて auto を使う場合は除く。）

なお、Eigen の内部ではこの表現テンプレートを用いて効率の良い演算の仕方を考える機構が入っているそうです。

Eigen を含むクラスやコンテナ

参考：

• Structures Having Eigen Members : http://eigen.tuxfamily.org/dox/group__TopicStructHavingEigenMembers.html
• Using STL Containers with Eigen : http://eigen.tuxfamily.org/dox/group__TopicStlContainers.html

Eigen の動的でない行列・ベクトル（Eigen::Vector3dとか）を含むクラスを作ったり、std::vector などのコンテナを使う際には、通常通りの実装ではアラインメントの問題が発生します。
Eigen では演算速度向上のためデータの保存領域がメモリ上で扱いやすい並びになるよう調節する機能がついているのですが、Eigen の動的でない行列・ベクトルを含むクラスやコンテナではそれが上手くいかないときもあるというのが原因です。

この場合、まず、動的でない行列やベクトルを含むクラスについては

class Test {
    Eigen::Vector2d vec;
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
};

のように public のところに EIGEN_MAKE_ALIGNED_OPERATOR_NEW というマクロを打っておく必要があります。（このマクロを展開すると問題のない new を定義してくれるそうです。）

動的でない行列やベクトル、およびそれらを含むクラスをコンテナへ格納する場合は、特殊なアロケータが必要になります。

std::map<int, Eigen::Vector4f, std::less<int>, 
     Eigen::aligned_allocator<std::pair<const int, Eigen::Vector4f> > >

これは参考のホームページの例の引用ですが、このように Eigen::aligned_allocator をテンプレート引数に加えておく必要があります。さらに、std::vector については <Eigen/StdVector> というヘッダーを読み込んでから同様の定義をする必要があります。

#include <Eigen/StdVector>
...
std::vector<Eigen::Vector3d, std::aligned_allocator<Eigen::Vector3d> > vec;

動的な行列・ベクトル（Eigen::VectorXdとか）ではこの問題を気にしなくても大丈夫です。

Eigen の値渡し

参考：Passing Eigen objects by value to functions : http://eigen.tuxfamily.org/dox/group__TopicPassingByValue.html

Eigen の動的でない行列やベクトルを関数へ値渡しするのもアラインメントの問題を招く場合があります。関数の引数では参照渡しかconst参照渡しをするという C++ での慣習が、Eigen ではクラッシュさせないために守らなければならないルールとなっているということを心にとめておいてください。
なお、関数からの返り値は値渡しで問題ないそうです。

これについても動的な行列やベクトルでは問題ありませんが、動的にするようなサイズのデータを値渡しするのは無駄なコピーを生成するためお勧めしません。（Eigen の各種演算は表現テンプレートを用いた遅延評価を用いてこの問題をうまく回避しているようです。）

終わりに

ここまで、Eigen の密行列関連の機能の一部を紹介してきました。
一応1年くらいこのライブラリを使っているものの、まだまだ使っていない機能が多く、至らない部分もあると思いますが、加筆・訂正して欲しい部分などありましたら教えてください。