はじめに
XGBoost等、高度で強力なアルゴリズムのベースになっている決定木について
単純なアルゴリズム故に殆ど学ばず知ったつもりになっていたのですが、実際よく分かってなかったので改めて調べてみました。
せっかくなので知識の確認と備忘用に纏めます。
言葉の定義
決定木は分類にも回帰にも使えます。
ここからは分類用は分類木、回帰用は回帰木と表現します。
決定木の話になると不純度という言葉が出てきます
私は全く知りませんでしたが、これは特定の定式があるワケではなく
モデルにより個別に定義する関数になります。
分類の場合は不純度としてジニ係数やクロスエントロピー誤差が使われたり
回帰の場合は二乗誤差を用いたりします。
評価関数とか活性化関数のように、何を用いるかはケースバイケースになります。
具体的なケースで考える
レストランにて
会計金額から客の性別を予測する分類木
客の性別から会計金額を予測する回帰木
を作りたいとします。
以下のようなデータセットがあります。
| 性別 | 会計金額 |
|---|---|
| 男性 | 2300円 |
| 男性 | 2200円 |
| 男性 | 2180円 |
| 女性 | 1500円 |
| 女性 | 1470円 |
| 女性 | 1220円 |
一目見てわざわざ決定木なんて使わなくても
1400円くらいの会計金額なら女性、2200円くらいなら男性と分かりますね
では実際に決定木は、どのようなプロセスでその結論に至るのでしょうか
分類木のケース
会計金額から性別を予測するケースで考えます。
男性か女性の2クラス分類なので、分類木の出番ですね。
分類木の場合、与えられたサンプルデータを分割して、分割後のデータの不純度が最も小さくなる点を探します。
今回のケースだと、スッパリ男性と女性のデータを最もきれいに分けられる特徴量とその分岐点を探します。
不純度に関しては上述した通り分類の場合は、ジニ係数やクロスエントロピー誤差等が用いられます
ジニ係数\\
E(t) = 1 - \sum_{n=1}^{N}P^2(C_n|t)\\
交差エントロピー誤差\\
E(t) = -\sum_{n=1}^{N}P(C_n|t)log_eP(C_n|t)\\
自分は数学の知識が無いので、いきなり何の定義も無しにこういう式が出ると吐き気がします。
定義の説明をしつつ、具体的な数値を入れて考えていきます。
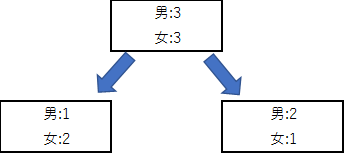
例えば、何らかの分割基準で分割を行った時に以下の様にサンプルデータが分割されたとします
この時の左側の箱(男:1 女:2)のジニ係数とクロスエントロピーを計算してみます。
まずふたつの関数に共通している $P(C_n|t)$は全体 $t$ に対する各クラス $C_n$ の割合を表す関数です。
つまり$P(C_n|t) = \frac{C_n}{t}$ になります。
ジニ係数
男女それぞれ$P(C_n|t) = \frac{1}{3},\frac{2}{3}$です
ジニ係数の式では$P^2(C_n|t)$ と二乗が付いてるのでそれぞれ二乗して $\frac{1}{9},\frac{4}{9}$ です。
$\sum$が付いてるので、他のクラスの結果を総和して1から引きます。
$1 - (\frac{1}{9} + \frac{4}{9}) = \frac{4}{9} = 0.4444...$
これが左の箱のジニ係数になります。
クロスエントロピー誤差
$P(C_n|t)$は男女それぞれ$\frac{1}{3},\frac{2}{3}$でした
これに$log_eP(C_n|t)$を乗算して総和するので計算してみると
$- ((-0.3658...) + (-0.2703....)) = 0.6361$
ジニ係数もクロスエントロピー誤差も、仮に箱の中身が完全に単一のクラスのみになると、どちらも0になり
低ければ低い程良い指標と言えます。
不純度を最小化する分割点を探す
分割の良さをどのように評価するのかは分かりました。
次に分割点をどのように探すのかが問題になります。
今回のケースでは男女の分類を行う為に与えられているデータ(特徴量)は会計金額のみです。
まずは、この会計金額をソートして、データ間の中点を計算します。
あとは、この中点でデータを区切って不純度を計算して各分割点での不純度を計算します。
この時、不純度は左右の別々に計算して、左右に割り振られたサンプル数で加重平均した物を、この分割での不純度とします。
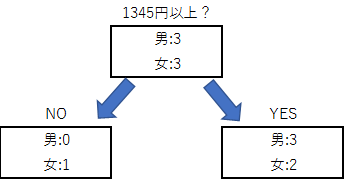
今回のケースだと会計金額1840円以上かどうかで、不純度0でスッパリ男女3:3に分けられるので、それ以外の点の不純度は計算しないでおきます。
もし、特徴量が複数ある場合は、他の特徴量も同様にソートして分割点毎の不純度を計算して最良の特徴量と分割点を探します。
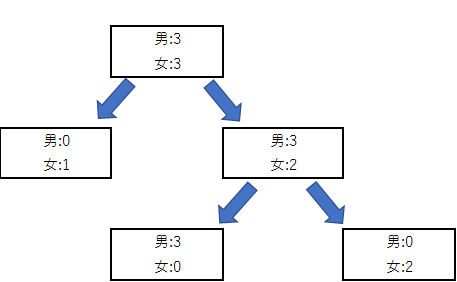
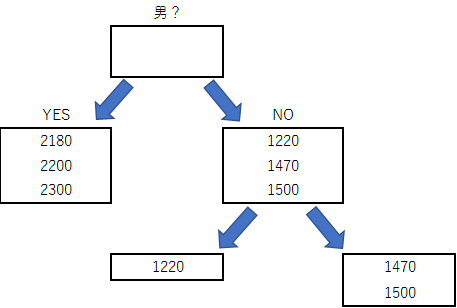
また、1回の分割だけでは完全に男女を分ける事が出来ない場合は、そこから更に以下の様に分割を継続します。
延々と分割を繰り返すと不純度はどんどん低下しますが、モデルとしては訓練データに過学習した状態になってしまいます。
対策として適当なところで分割をヤメたり、既にある分割を無効にしたりする事を剪定と呼びます。
回帰木のケース
回帰木の場合も分類の場合と大きく変わりません
最も不純度が低くなる特徴量と分割点を探して、分割を繰り返すのですが
回帰木の場合は不純度として、同じ箱に分類されたサンプル平均との**MSE(二乗平均誤差)やRMSE(二乗平均平方誤差)**など
回帰モデルの評価関数で使用される関数が使用されます。
MSE\\
\frac{1}{N}\sum_{n=1}^{N}(y_n - y)^2\\
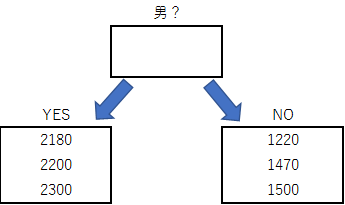
今回のケースだと、使える特徴量が性別しかないので、否応なく3:3に分かれてしまい、それ以上分割できません。
しかし、仮に他にも特徴量として与えられたデータがあれば、分類の時と同様に分割が続きます。
終わり
XGBoostやLightGBMなど強力な予測モデルのベースになっている決定木
仕組みが単純なので、分かった気になっていましたが、調べてみると不純度の定義等あまりよく理解出来ていませんでした。
また、分類木と比べて回帰木の解説があまり見られず、回帰木の場合の分割基準ってどうやってるんだろうと気になったので調べて纏めました。
気を付けているつもりですが、間違いがありましたらご指摘頂けますと幸いです。