Go to Qiita Advent Calendar 2024 Top
LoginSignup
4
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@MuAuan(ムー ウワン)

【OculusGo】Solar_Systemを太陽系のサイズに基づいて再現した♬

Last updated at Posted at 2018-07-01

solar_system.jpg
【OculusGo】よりリアルな精度のソーラーシステム♬
<img src="http://img.youtube.com/vi/dgHcjptHveQ/0.jpg"

※画像をクリックするとYouTube動画につながります

###やったこと
（１）スケール1／？？の太陽系にしてみた。
（２）万有引力による円運動とみなしてスケール因子を導出
（３）一般的な運動方程式にスケール因子を導入する
（４）太陽系を扱うための単位系
（５）基本的なコード
（６）衛星をもつ惑星
（７）尾を持つ彗星
（８）動くのか？
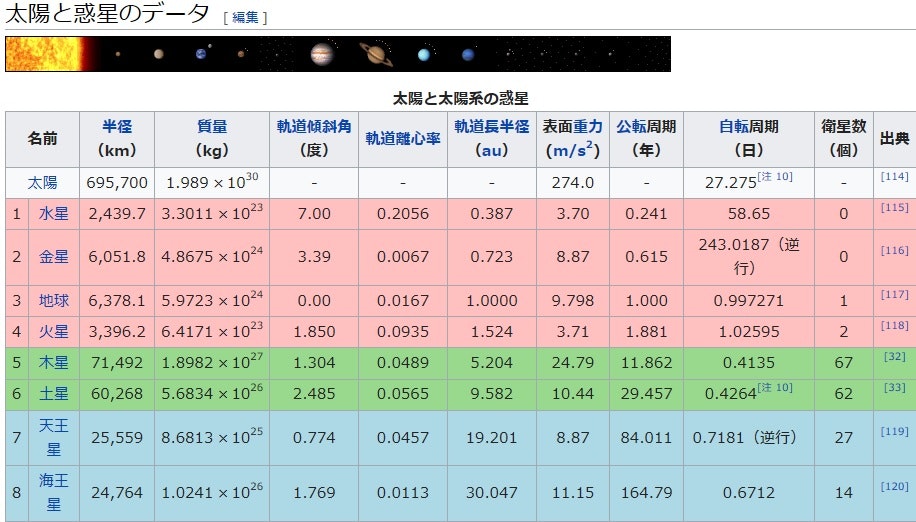
###（１）スケール1／？？の太陽系にしてみた。
太陽系のスケールは、Wikipediaより以下のとおり
Solar_size.jpg

これをこのまま再現。。はできないので、軌道半径はこのauを使い、質量は$10^{21}㎏$単位として換算した。また、半径というか直径は実は当たり判定の大きさが意味があるが、これはあまりにも小さいので視覚的に見える程度の大きさにした。相対的な大きさも難しいのである程度考慮して決めた。
ちなみに、上記をそのまま踏襲すると以下の大きさであるが、このアプリでは以下の表のようにした。つまり内惑星は1／5M、外惑星は1/10M、冥王星は1/5Mにした。

惑星 水星 金星 地球 火星 小惑星 木星 土星 天王星 海王星 冥王星 小惑星２
半径(Mm) 2.4 6.9 6.4 3.4 - 71.5 60.3 25.6 24.8 1.2 -
直径 0.48 1.38 1.28 0.68 - 7 6 2.6 2.5 0.24 -
###（２）万有引力による円運動とみなしてスケール因子を導出
一番簡単に考えると、太陽系はほぼ惑星が中心力による円運動、中心力は万有引力。
ということで、円運動は、角速度$ω=dθ/dt$とすると、 
F=mrω^2　　　（１）

v=rω　　　　（２）

T＝2π／ω　　　　（３）

a=rω^2　　　　（４）

そして万有引力は、万有引力定数$G=6.67×10^{-11}(N^2m^2/kg^2)$とすると

F=GMm/r^2　　　　（５）

（１）と（５）から

v=(GM/r)^{1/2}    （６）

T=2πr(GM/r)^{-1/2}    （７）

このまま動かすと、太陽系のスケールは単に距離単位としてauを導入して小さくなったとはいえ、周期が長すぎる。
###（３）一般的な運動方程式にスケール因子を導入する
ということで、適当なスケール因子$f_{c}$を万有引力定数に$G=f_c^2g$として導入し、太陽系を支配している力を強くして運動を加速することとする。
※【重要】$f_{c}^2$としたのは、式（７）より周期Tが$～G^{1/2}$であり、$～f_cg^{1/2}$と考え易くするためである。
こうして以下の運動方程式が得られる。

F=ma=f_c^2gMm/r^2　　　　（８）

そして、力のx, y, z方向の各成分は

F_{x}=f_c^2gMm/r^2・x/r, 　F_{y}=f_c^2gMm/r^2・y/r, 　F_{z}=f_c^2gMm/r^2・z/r 　　　　（９）

※【重要】式（７）まではスケール因子を導入するにあたって円運動を仮定して導出したが、式（８）は円運動を仮定していない万有引力による物体の一般的な運動方程式であり、式（８）以降の結果は円運動を仮定しているわけではない。

接線方向x, 公転軸方向y, 中心方向zの初速度を以下の通りとする。
※初期状態をあるｚ軸方向に並べているときの座標であり単純な直交座標である。
※どういう風に太陽系が始まったかは分からない。適当な時期から開始する場合は、それぞれ物体の位置や初速度を変化させればよい。ここではまずは簡単な初期条件とする。

v_{x}=f_{c}(gM/r)^{1/2},　v_{y}=0,　v_{z}=0　　　　（１０）

###（４）太陽系を扱うための単位系
太陽系みたいに大きなものをシミュレートするとき大切なのは、サイズをどうするか。
つまり、単位系をどうするかです。
ここでは、いわゆるMKS単位系(m, kg, sec)からAUS単位系（au, $10^{21}kg$, sec）という普通とは異なる単位系でやろうと思う。
※質量は$10^{23}$や地球の質量を１（$6.0*10^{23}$）を採用でもいいけど、小さな惑星と大きな惑星の質量比が大きくて計算誤差を生みやすいので、$10^{21}$とした

万有引力定数$G=6.67×10^{-11}(N^2m^2/kg^2)$の換算
MKS単位系からAUS(au-umass-S)単位系に変換する。

$N ⇒ kgm/s⇒10^{-21}umass(1/1.5*10^{-11}au)/s$

$N = 1/1.5*10^{-32}　AUS単位系$

$G = 6.6710^{-11}((1/1.510^{-32})^2(AUS)(1/1.510^{-11}au)^2/(10^{-21}umass)^2$
$= 1.3210^{-11} (AUS)$

$m = 1/(1.5*10^{11}) au$

$kg = 10^{-21} umass$

$M = 1.9910^{30}kg=1.9910^{9} umass$

$GM = 1.32* 1.99 *10^{-11+9}$
$= 2.64 * 10^{-2} (AUS)$

$F = GMm/r^2$
$ =1.32*10^{-11}*Mm/r^2$

$v_{x}=f_{c}(gM/r)^{1/2}$
$=f_{c}3.63*10^{-6}(M/r)^{1/2}$
この項、実際のシミュレーションでは数値をいじっているので再現するときは再計算してください
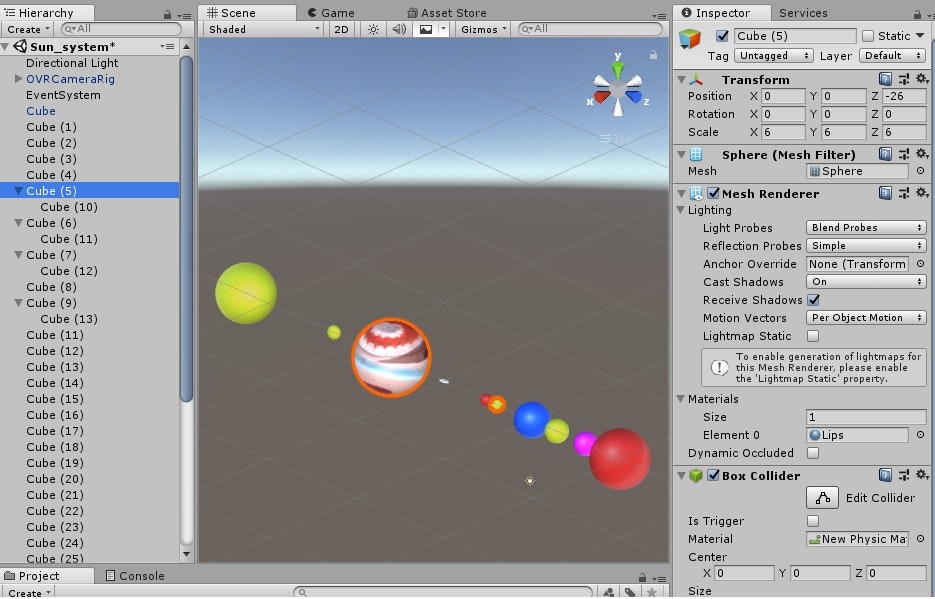
###（５）基本的なコード
惑星を動かすコードは以下のとおり、太陽は不動とし、惑星間相互作用は無視（衝突以外）した。

MoveCube.cs
using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class MoveCube : MonoBehaviour {
    [SerializeField]
    private GameObject obj;
    [SerializeField]
    private GameObject Cube;
    private Vector3 m_NewForce;
    private float gM;
    private float r;
    private float x;
    private float y;
    private float z;
    private float m;
    private float fc;

    // Use this for initialization
    void Start () {
        this.obj.transform.GetComponent<Rigidbody>().AddTorque(new Vector3(0, 5f, 5f));
        // objに与える力を定義する。WorldSpaceの（0，0，0）に向かうベクトルに比例した力としている
        // objに力を加える
        gM = 0.0264f;
        fc = 10f;
        x = obj.transform.localPosition.x;
        y = obj.transform.localPosition.y;
        z = obj.transform.localPosition.z;   
        r = Mathf.Sqrt(x*x + y*y + z*z);
        this.obj.transform.GetComponent<Rigidbody>().velocity = new Vector3(-fc*Mathf.Sqrt(gM/r), 0, 0);
    }
	
	// Update is called once per frame
	void Update () {
        x = obj.transform.localPosition.x;
        y = obj.transform.localPosition.y;
        z = obj.transform.localPosition.z;   
        r = Mathf.Sqrt(x*x + y*y + z*z);
        m = obj.transform.GetComponent<Rigidbody>().mass;

        obj.transform.GetComponent<Rigidbody>().AddTorque(new Vector3(0, 1f, 5f));
        // objに与える力を定義する。WorldSpaceの（0，0，0）に向かうベクトルに比例した力としている
        r = Mathf.Sqrt(x*x + y*y + z*z);
        m_NewForce = new Vector3(-gM*fc*fc*m*x/(r*r*r) , -gM*fc*fc*m*y/(r*r*r), -gM*fc*fc*m*z/(r*r*r));

        // objに力を加える
        obj.transform.GetComponent<Rigidbody>().AddForce(m_NewForce, ForceMode.Impulse);
    }
}

衛星を持つ惑星もリコイルは無し、単に惑星－衛星間相互作用のみを考慮した。

MoveCube_sat.cs
using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class MoveCube_sat : MonoBehaviour
{
    [SerializeField]
    private GameObject obj;
    [SerializeField]
    private GameObject obj2;
    private Vector3 m_NewForce;
    private float gMm;
    private float r;
    private float x;
    private float y;
    private float z;
    private float m;
    private float M;
    private float fc;

    // Use this for initialization
    void Start()
    {
        //this.obj.transform.GetComponent<Rigidbody>().AddTorque(new Vector3(0, 5f, 5f));
        // objに与える力を定義する。WorldSpaceの（0，0，0）に向かうベクトルに比例した力としている
        // objに力を加える
        M = this.obj.transform.GetComponent<Rigidbody>().mass;
        m = this.obj2.transform.GetComponent<Rigidbody>().mass;
        gMm = 1.32f*M*m;  //10^{-11}
        fc = 0.00008f;
        x = this.obj2.transform.localPosition.x;
        y = this.obj2.transform.localPosition.y;
        z = this.obj2.transform.localPosition.z;
        r = Mathf.Sqrt(x * x + y * y + z * z);
        this.obj.transform.GetComponent<Rigidbody>().velocity = new Vector3(-1f * fc * Mathf.Sqrt(gMm / r), 0, 0);
    }
    // Update is called once per frame
    void Update()
    {
        x = this.obj2.transform.localPosition.x;
        y = this.obj2.transform.localPosition.y;
        z = this.obj2.transform.localPosition.z;
        //obj.transform.GetComponent<Rigidbody>().AddTorque(new Vector3(0, 1f, 5f));
        // objに与える力を定義する。WorldSpaceの（0，0，0）に向かうベクトルに比例した力としている
        r = Mathf.Sqrt(x * x + y * y + z * z);
        m_NewForce = new Vector3(-gMm * fc * fc * x / (r * r * r), -gMm * fc * fc * y / (r * r * r), -gMm * fc * fc * z / (r * r * r));
        // objに力を加える
        obj.transform.GetComponent<Rigidbody>().AddForce(m_NewForce, ForceMode.Impulse);
    }
}

コードは参考としてあげています。実際動かしてみるとCPUなどにより再現性が変化するようです。例えばPCとOculusGoでは結果が異なります
###（６）衛星をもつ惑星
一番、大きい話は相互作用。
惑星が衛星を持てるかどうかは、一定以上の質量や太陽からの適当な距離が必要である。
それらの理由の多くは、このリコイルと太陽から独立して捕獲していけるかということが重要である。ということで、ここでは惑星と衛星の相互作用や質量を平等に扱うことで惑星が衛星を持てるのかシミュレートしてみた。
因みに、一度衛星を持つ惑星を作ってうまく動くと、それをその場でDupilicateで増幅できる。またAssetsに保存することにより、再利用で追加もできる

MoveCube_sat.cs
using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class MoveCube_sat : MonoBehaviour
{
    [SerializeField]
    private GameObject obj;
    [SerializeField]
    private GameObject obj2;
    private Vector3 m_NewForce;
    private Vector3 m_NewForce1;
    private float gMm; 
    private float r;
    private float x;
    private float y;
    private float z;
    private float m;
    private float M;
    private float fc;

    // Use this for initialization
    void Start()
    {
        //this.obj.transform.GetComponent<Rigidbody>().AddTorque(new Vector3(0, 5f, 5f));
        // objに与える力を定義する。WorldSpaceの（0，0，0）に向かうベクトルに比例した力としている
        // objに力を加える
        M = obj.transform.GetComponent<Rigidbody>().mass;
        m = obj2.transform.GetComponent<Rigidbody>().mass;
        gMm = getgMm();
        fc = 3f;

        x = obj.transform.localPosition.x; //- obj2.transform.localPosition.x;
        y = obj.transform.localPosition.y; //- obj2.transform.localPosition.y;
        z = obj.transform.localPosition.z; //- obj2.transform.localPosition.z;
        r = calcRadius(x, y, z);
        obj.transform.GetComponent<Rigidbody>().velocity = new Vector3(x: 10f * fc * Mathf.Sqrt(gMm / r), y: 0, z: 0);
    }

    // Update is called once per frame
    void Update()
    {
        x = obj.transform.localPosition.x; //- obj2.transform.localPosition.x;
        y = obj.transform.localPosition.y; // - obj2.transform.localPosition.y;
        z = obj.transform.localPosition.z; // - obj2.transform.localPosition.z;

        // objに与える力を定義する。WorldSpaceの（x1，y1，z1）に向かうベクトルに比例した力としている
        r = calcRadius(x,y,z);

        m_NewForce = new Vector3(-gMm * fc * fc * x / (r * r * r), -gMm * fc * fc * y / (r * r * r), -gMm * fc * fc * z / (r * r * r));
        m_NewForce1 = new Vector3(gMm * fc * fc * x / (r * r * r), gMm * fc * fc * y / (r * r * r), gMm * fc * fc * z / (r * r * r));
        // objに力を加える
        obj.transform.GetComponent<Rigidbody>().AddForce(m_NewForce, ForceMode.Impulse);
        obj2.transform.GetComponent<Rigidbody>().AddForce(m_NewForce1, ForceMode.Impulse);
    }

    private float calcRadius(float x,float y, float z)
    {
        r = Mathf.Sqrt(x * x + y * y + z * z);
        return r;
    }
    private float getgMm()
    {
        M = obj.transform.GetComponent<Rigidbody>().mass;
        m = obj2.transform.GetComponent<Rigidbody>().mass;
        gMm = 1.32f * M * m * 0.0000000008f;
        Debug.Log(gMm);
        return gMm;
    }
}

###（７）尾を持つ彗星
ここは尾っぽをどうするかに尽きる
実際の彗星は太陽からの太陽風を受けて、だんだん尾っぽが長く大きく成長する。しかもしっぽの方向は後ろ向きではなく、この太陽風に流される（太陽と反対向き）方向に延びる。
※ここまで書いたらそれ実現したんでしょ。。。ごめんなさい、今回はあきらめました

とはいえ、一応尾っぽをつけて、彗星っぽい軌道を動いて二度と見えない状況は再現できました。
コードは惑星とほぼ同一です。
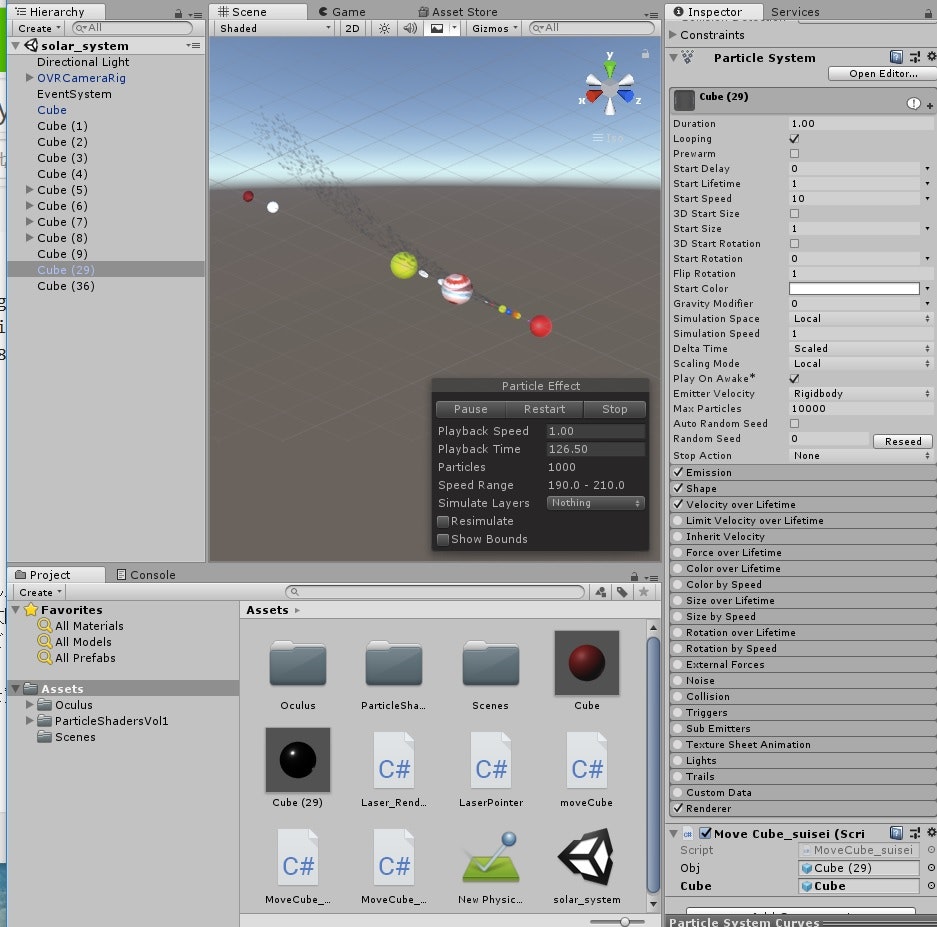
一か所、「Add Component-Effects-particle system」でparticle systemを追加する。
これを尻尾とみなして調整する。で、以下のような設定でとりあえず彗星ぽくなった。
※これ設定次第でしっぽが回ったりするので、うまくやれば近づくとき。。。面倒なので今回はやめました
suisei_settings.jpg
###（８）動くのか？
実は、結構惑星やら衛星やら小惑星やら増やしたので動くのか心配でしたが、どうにか動きました。
ということで、とりあえずこんな感じです。
※見てると時間がすぐすぎてしまいます
【OculusGo】よりリアルな精度のソーラーシステム♬
<img src="http://img.youtube.com/vi/dgHcjptHveQ/0.jpg"

※画像をクリックするとYouTube動画につながります
###まとめ
・Solar_Systemを実際の太陽系のサイズに基づいて再現した
・衛星を持つ惑星のシミュレーションを実施した
・彗星をparticle systemで実装した
・外惑星の公転周期はこのサイズでも長い。。。
・相互作用としてばねに比較して万有引力は近接相互作用であり、脱出速度が小さいため、トラップされ難くかつ惑星も衛星も不安定である
・内惑星や衛星は特に不安定である

・各パラメータは絶妙な数値となっていて、Solar_Systemが成立するのはかなり選ばれた状況にあると感じた
・ロケットを飛ばして他の惑星まで往復するシミュレーションをやろうと思ったが、今回は実施しなかった
・実際の太陽系はもっと複雑であるが、その一部を見て予測可能なシミュレーションをやりたい
・次はこういうのだね。。。
太陽系惑星形成論が持ち越してきた問題に挑む

4
2
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
4
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?