【将棋AI】「将棋AIで学ぶディープラーニング」を読む♪～VGG利用のPolicy_Valueネットワーク

第廿二夜も、本書から逸脱するが、[昨夜の延長としてVGGLikeモデル](https://qiita.com/MuAuan/items/539f5cc8944cc6043453)を利用したPolicy_valueネットワークモデルを作成して強さを見た。 ###やったこと （１）VGGLikeモデルを利用したPolicy_valueネットワークモデル （２）パラメータサイズと収束性について （３）強くなったのか？？ ###（１）VGGLikeモデルを利用したPolicy_valueネットワークモデル 今回の場合、昨夜のVGGLikeモデルから想像つくと思いますが、以下の通りです。

from chainer import Chain
import chainer.functions as F
import chainer.links as L
from pydlshogi.common import *

ch = 192
fcl = 256
class PolicyValueNetwork(Chain):
    def __init__(self):
        super(PolicyValueNetwork, self).__init__()
        with self.init_scope():
            self.conv1_1 = L.Convolution2D(104, ch, 3, pad=1)
            self.conv1_2 = L.Convolution2D(ch, ch, 3, pad=1)
            self.conv2_1 = L.Convolution2D(ch, ch*2, 3, pad=1)
            self.conv2_2 = L.Convolution2D(ch*2, ch*2, 3, pad=1)
            self.conv3_1 = L.Convolution2D(ch*2, ch*4, 3, pad=1)
            self.conv3_2 = L.Convolution2D(ch*4, ch*4, 3, pad=1)
            self.conv3_3 = L.Convolution2D(ch*4, ch*4, 3, pad=1)
            self.conv3_4 = L.Convolution2D(ch*4, ch*4, 3, pad=1)
            # policy network
            self.l13=L.Convolution2D(in_channels = ch*4, out_channels = MOVE_DIRECTION_LABEL_NUM, ksize = 1, nobias = True)
            self.l13_bias=L.Bias(shape=(9*9*MOVE_DIRECTION_LABEL_NUM))
            # value network
            self.l13_v=L.Convolution2D(in_channels = ch*4, out_channels = MOVE_DIRECTION_LABEL_NUM, ksize = 1)
            self.l14_v=L.Linear(9*9*MOVE_DIRECTION_LABEL_NUM, fcl)
            self.l15_v=L.Linear(fcl, 1)

    def __call__(self, x):
        h = F.relu(self.conv1_1(x))
        h = F.relu(self.conv1_2(h))
        #h = F.max_pooling_2d(h, 2, 2)
        #h = F.dropout(h, ratio=0.25)
        h = F.relu(self.conv2_1(h))
        h = F.relu(self.conv2_2(h))
        #h = F.max_pooling_2d(h, 2, 2)
        #h = F.dropout(h, ratio=0.25)
        h = F.relu(self.conv3_1(h))
        h = F.relu(self.conv3_2(h))
        h = F.relu(self.conv3_3(h))
        h = F.relu(self.conv3_4(h))
        #h = F.dropout(h, ratio=0.25)
        h13 = self.l13(h)
        # policy network
        h13 = self.l13(h)
        policy = self.l13_bias(F.reshape(h13, (-1, 9*9*MOVE_DIRECTION_LABEL_NUM)))
        # value network
        h13_v = F.relu(self.l13_v(h))
        h14_v = F.relu(self.l14_v(h13_v))
        value = self.l15_v(h14_v)
        return policy, value

###（２）パラメータサイズと収束性について
やはり、上記ネットワークモデルはサイズが大きく、収束時間等は以下のとおりです。

名称	loss	一致率（方策）	一致率（価値）	備考
VGGLike	2.37443	0.4219189	0.69108087	VGGLike8層
ResnetSimple40※	2.29075	0.4325099	0.6906338	Resnet２０block４３層
ResnetSimple20	2.308355	0.4326057	0.6941468	Resnet１０block２３層
ResnetSimple10	2.360802	0.42507267	0.6948055	Resnet５block１３層
ResnetTry30	2.27104	0.43431032	0.6986858	ResnetTri10block３３層
ResnetVGGLike5	2.279315	0.43526843	0.69514084	ResnetVGGLike５block１９層

model	time/epoch	層	params/MB
VGGL8	90：52	８層	78.72
S43	57：10	４３層	49.73
VGGL19	45：19	１９層	27.74
S23	37：59	２３層	25.61
S13	30：30	１３層	13.56
やはり、今回のVGGLikeモデルはパラメータも多く、時間も大幅にかかることとなっている。
そして、dropoutを使っている所為か、パラメータが多い割にはあまり一致率も上がってはいない。
###（３）強くなったのか？？
数字が物語るように、もう一つ強いとはいいがたく、そして以下のような面白い勝負となったものもある。
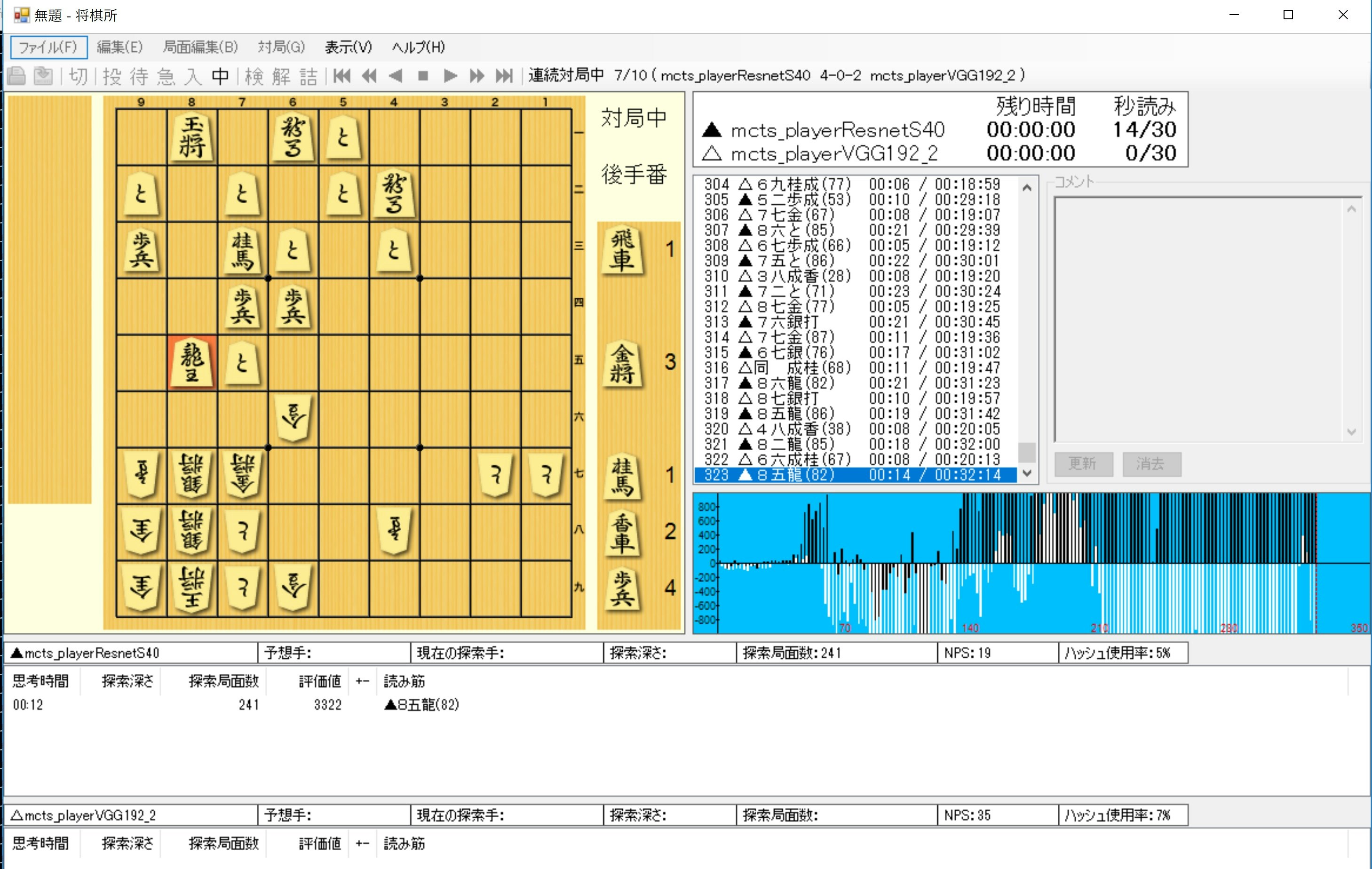
###まとめ
・VGGLikeなPlocy_valueのネットワークモデルでフィッティングしてみた
・パラメータが多くなり、時間がかかる割にあまり強くはならなかった

・ひとつの壁にぶつかったと感じている