【PID入門】制御して遊んでみた♬

PID制御は、大昔からある技術らしい。
そこで、丁寧に定式化して遊んでみたのでまとめておく。

【参考】
①PID controller
②PID制御

簡単には、以下のグラフで表せる。上記参考①より
[By Arturo Urquizo -](http://commons.wikimedia.org/wiki/File:PID.svg, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=17633925)

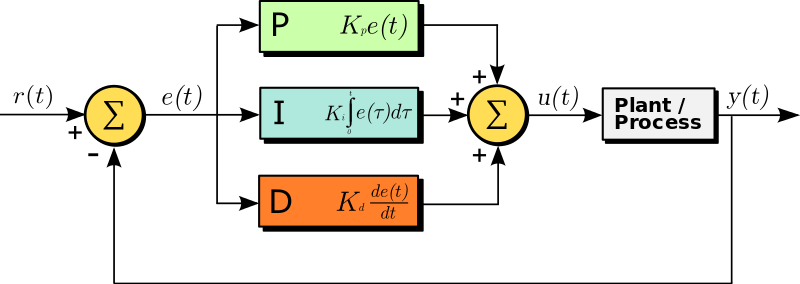
ここで、それぞれの量は以下のように定義される。

\begin{align}
r(t)&;目標量\\
y(t)&;操作後、対象プラントやプロセスの現在量\\
e(t)&=r(t)-y(t);現在量-目標量で計算される残差\\
u(t)&=P+I+D; 操作量\\
          &;対象プラントやプロセスに対する操作\\
　　      &;温度上げ下げのために流す電流値やハンドルやバルブ操作のための角度とか、。。\\
P&=K_pe(t); 比例制御\\
I&=K_i\int_0^t e(\tau )d\tau; 積分制御\\
D&=K_d\frac{de(t)}{dt}; 微分制御\\
\end{align}

ここでコンピュータ制御の場合$y(t)$が離散値になるため、積分制御と微分制御は以下のように数値積分及び数値微分で定義するのが良い。
サンプリング時刻$t=t_n$において、以下のように置く。
なお、数値微分はさらに高次のものでもよいが、実用性・反応性を考慮すると以下で良い。

\int_0^te(\tau)d\tau = \Sigma_{i=0}^ne(t_i)\Delta t\\
(\frac{de(t)}{dt})_{t_n}=\frac{e(t_n)-e(t_{n-1})}{\Delta t}\\
\Delta t = t_n-t_{n-1} ; const=1とする

###コードに落としてみる
まず、コントロール対象を以下とした。
すなわち、電気炉などの温度コントロールのイメージだ。

def ufunc(M,u=0,t=0):
    M0=0.2
    m=0.05
    return M - m*(M-M0-u)

コントローラー側は以下のPID制御を考える。
コードの一部は以下を参考にしています。
【参考】
PythonでPID制御をやってみる

t = 100
params_list = [(0,0,0)]  #Kp,Ki,Kdを設定
for kp,ki,kd in params_list:
    Kp,Ki,Kd=kp,ki,kd
    M0 = 2
    M=M0
    goal = 1.00
    e = 0.00 
    e1 = 0.00 
    u=0
    es=0
    x_list = []
    y_list = []
    u_list = []
    x_list.append(0)
    y_list.append(M)
    u_list.append(u)
    for i in range(1,t,1):
        M1 = M
        e1 = e
        e = goal - y_list[i-1] #偏差（e） = 目的値（goal） - 現在値
        es += e #積分は足し算
        u = Kp * e + Ki * es + Kd * (e-e1) #微分は引き算
        M = ufunc(M,u,i) #対象からのレスポンス
        x_list.append(i)
        y_list.append(M)
        u_list.append(u)
    plt.hlines([goal], 0, t, "red", linestyles='dashed') #ゴールを赤色の点線で表示
    plt.plot(x_list, y_list, color="b") #青色でレスポンスの時間変化を表示
    plt.title('Kp={}, ki={}, kd={}'.format(Kp, Ki, Kd))
    #plt.plot(x_list, u_list, color="black") #黒色で操作量を表示
    plt.ylim(-0.5, goal*2+0.2) #グラフの高さ調整
    plt.pause(0.2)
    plt.savefig("output/Kp,Ki,Kd/imageKp{}Ki{}Kd{}M0{}.png".format(Kp,Ki,Kd,M0))    
    plt.close()

###params_list = [(0,0,0)]で対象の反応を見る
t=0のとき、M=2として、室温M0=0.2とすると、以下のように徐々にM=0.2に近づいていく。

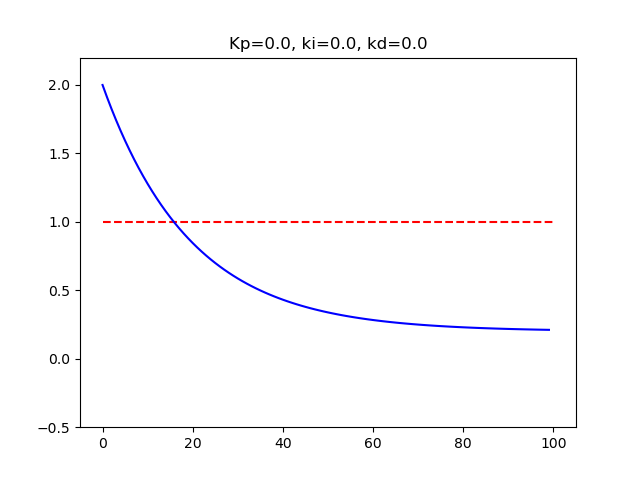
この系は以下の式で表される。

\frac{dM}{dt}=-m(M-M0)

解は、

M=M0+(2-M0)e^{-mt}\\
t=0のとき M=2

###ジーグラ・ニコルスの限界感度法
対象の臨界振動を見る
Wikipediaによれば、Ki = Kp / Ti、Kd = Kp・Tdとおくと、ジーグラ・ニコルスの限界感度法により、以下のように最適なパラメータが決まる。

制御手法	Kp	Ti	Td
P	0.50Ku	ー	ー
PI	0.45Ku	0.83Tu	ー
PID	0.6Ku	0.5Tu	0.125Tu
ここで、Ku、Tuは以下のように定義される。
「比例ゲインKpを0から徐々に大きくしていき、制御量が安定限界に達して一定振幅振動を持続するようになったところでKpの増加を止める。このときの比例ゲインをKu（限界感度）、振動周期をTu とすると、
上記の対象に対して限界振動を求めてみると、以下のようにKu=39のとき、Tu=2.0と求められる。

上の表をKi,Kdで書き換えると、

制御手法	Kp	Ki	Kd
P	0.50Ku	ー	ー
PI	0.45Ku	0.54Ku/Tu	ー
PID	0.6Ku	1.2Ku/Tu	3KuTu/40
###結果
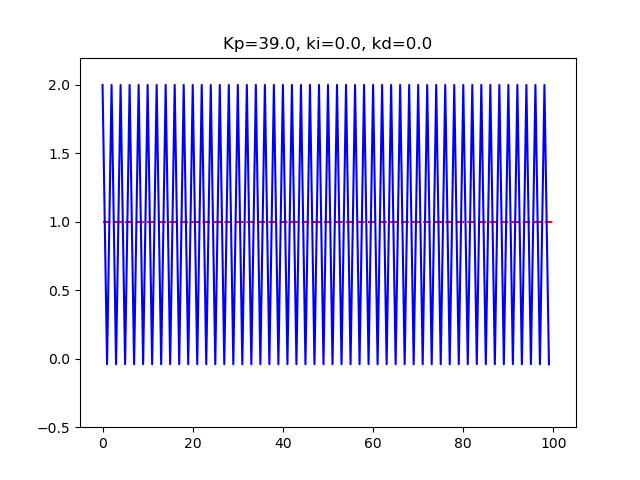
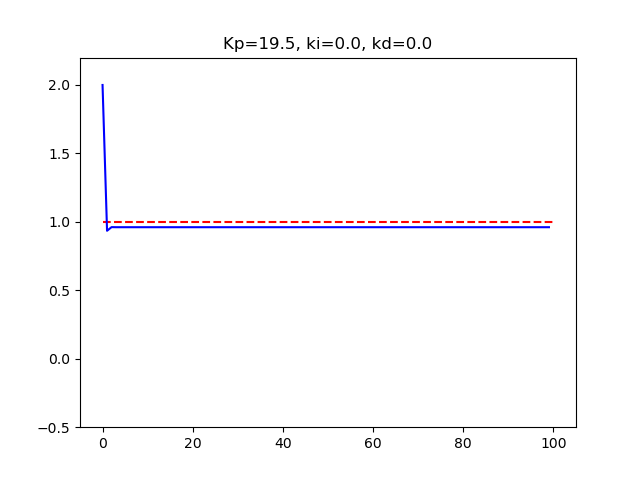
実際、上記パラメーターでやってみると、
P制御Kp19.5Ki0.0Kd0.0M02dt1
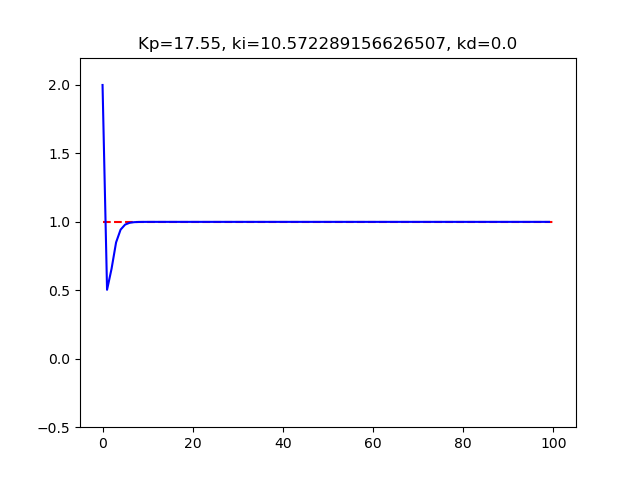
PI制御Kp17.55Ki10.57Kd0.0M02dt1
PID制御Kp23.4Ki23.4Kd5.85M02dt1
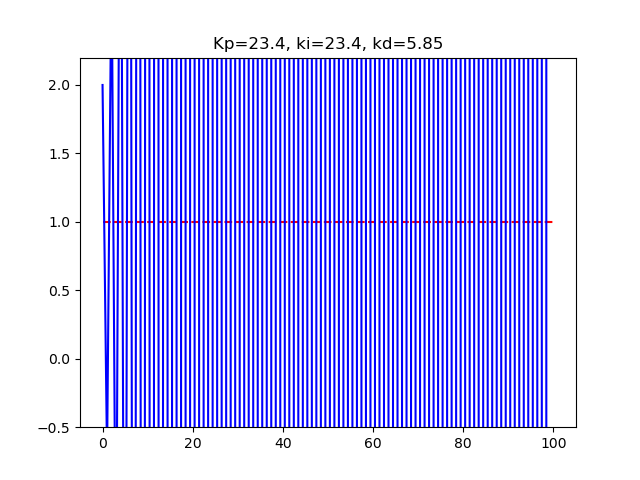
つまり、何らかの原因でPID制御は失敗
これは、丸目誤差が原因のようです。
###dt精度拡張と再計算
ということで、以下のようにdtを任意の刻みで計算できるように拡張します。

def ufunc(M,u=0,t=0,dt=1):
    M0=0.2
    m=0.05
    return M - m*(M-M0-u)*dt

t = 100
dt=0.1

Ku=39
Tu=2
params_list =[(0.5*Ku,0,0),(0.45*Ku,0.54*Ku/Tu,0),(0.6*Ku,1.2*Ku/Tu,3*Ku*Tu/40)]
for kp,ki,kd in params_list:
    Kp,Ki,Kd=kp,ki,kd
    ...
    for i in range(1,int(t/dt),1):
        ...
        e = goal - y_list[i-1] #偏差（e） = 目的値（goal） - 前回の実現値
        es += e*dt
        u = Kp * e + Ki * es + Kd * ((e-e1)/dt )
        M = ufunc(M,u,i,dt)

        x_list.append(i*dt)
        y_list.append(M)
        u_list.append(u)
        ...
    plt.savefig("output/Kp,Ki,Kd,dt/imageKp{}Ki{}Kd{}M0{}dt{}.png".format(Kp,Ki,Kd,M0,dt))    
    plt.close()

dt＝0.1にして再実施、思惑通りうまく描けました。
PID制御Kp23.4Ki23.4Kd5.85M02dt0.1

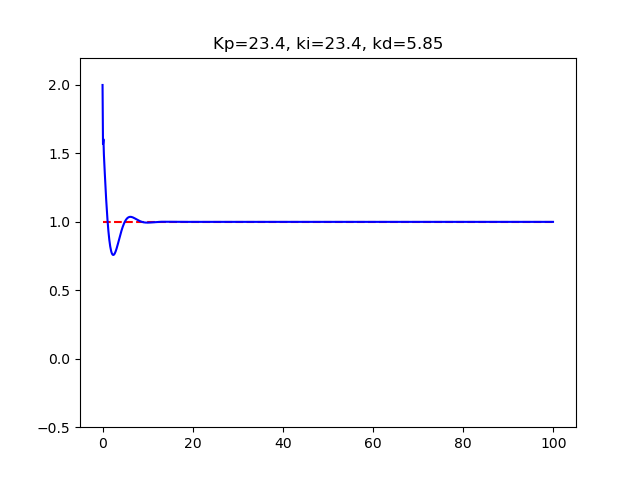
大きな変化は、t=0-10で終わっているので、dt刻みをこまかく計算できるようになったので、刻みdt=0.01で再計算してみます。
P制御　Kp19.5Ki0.0Kd0.0M02dt0.01

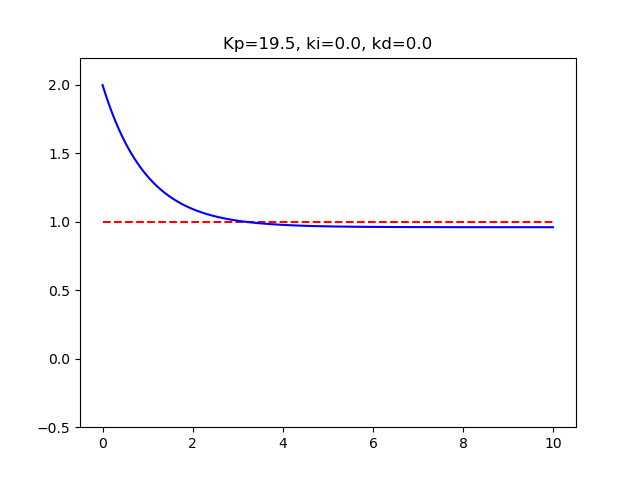
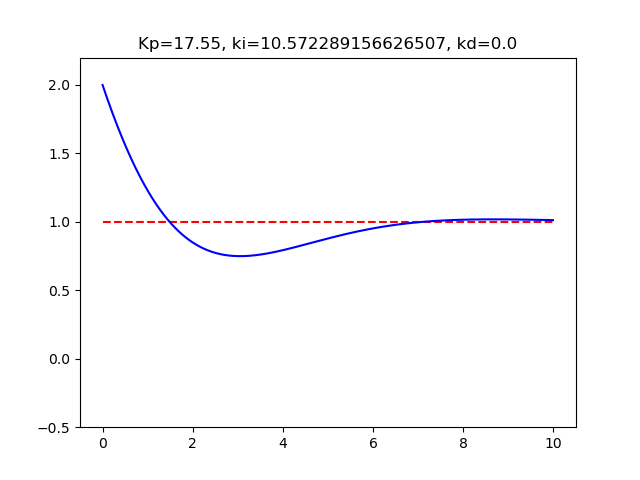
PI制御　Kp17.55Ki10.57Kd0.0M02dt0.01

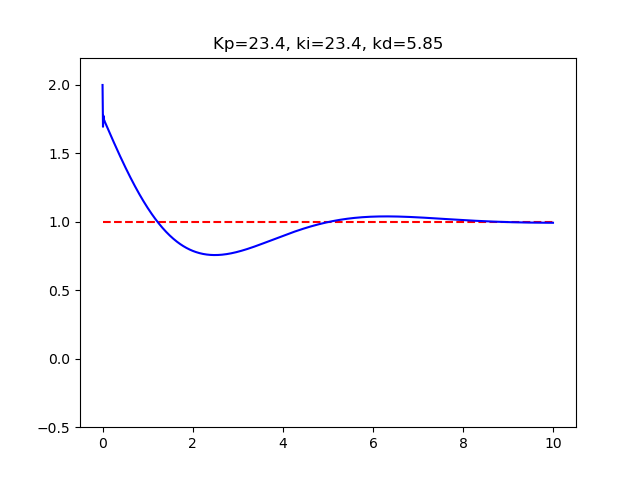
PID制御　Kp23.4Ki23.4Kd5.85M02dt0.01

###PID制御のグラフ再現
英語版Wikipediaの以下のグラフを再現してみる。

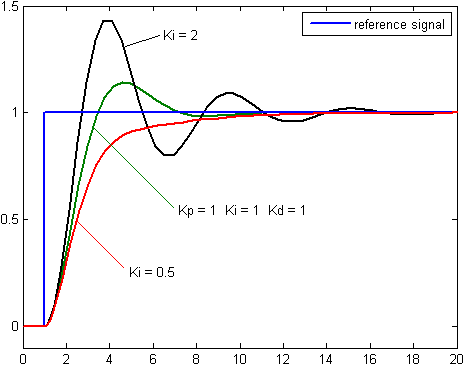
条件が描いてないようなので、一番ありそうな条件でいろいろ描いて見ると、以下の条件でKi依存性は、ほぼ似たような絵になりました。
※もっと条件を絞っていけば完全再現もできるだろうけど、ここで止めました
　このグラフで、十分にKiパラメーターを変化させたときの性質が見えます。

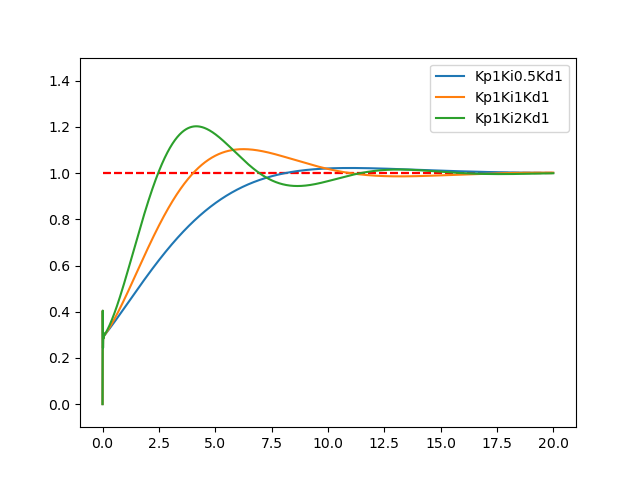
条件は、以下のとおり
制御対象は、
m=0.4と上記に比べると大き目の値にして、室温に相当するM0=0としました。

def ufunc(M,u=0,t=0,dt=1):
    M0=0
    m=0.4
    return M + m*u*dt - m*(M-M0)*dt

計算は、表記の通りと同じパラメーター値で計算しています。
グラフを凡例付きで３本同時描画しました。
グラフの描画範囲を合わせています。

t = 20
dt=0.01
params_list =[(1,0.5,1),(1,1,1),(1,2,1)]
for kp,ki,kd in params_list:
    Kp,Ki,Kd=kp,ki,kd
    M0 = 0
    M=M0
    goal = 1.00
    e = 0.00 
    e1 = 0.00 
    u=0
    es=0
    x_list = []
    y_list = []
    u_list = []
    x_list.append(0)
    y_list.append(M)
    u_list.append(u)
    for i in range(1,int(t/dt),1):
        M1 = M
        e1 = e
        e = goal - y_list[i-1] #偏差（e） = 目的値（goal） - 前回の実現値
        es += e*dt
        u = Kp * e + Ki * es + Kd * ((e-e1)/dt )
        M = ufunc(M,u,i,dt)
        x_list.append(i*dt)
        y_list.append(M)
        u_list.append(u)
    plt.hlines([goal], 0, t, "red", linestyles='dashed') #ゴールを赤色の点線で表示
    plt.plot(x_list, y_list,label="Kp{}Ki{}Kd{}".format(Kp,Ki,Kd)) 
    plt.legend()
    plt.ylim(-0.1, 1.5) #グラフの高さを調整
    plt.pause(0.2)
plt.savefig("output/Kp,Ki,Kd,dt/imageKp{}Ki{}Kd{}M0{}dt{}2.png".format(Kp,Ki,Kd,M0,dt))    
plt.close()

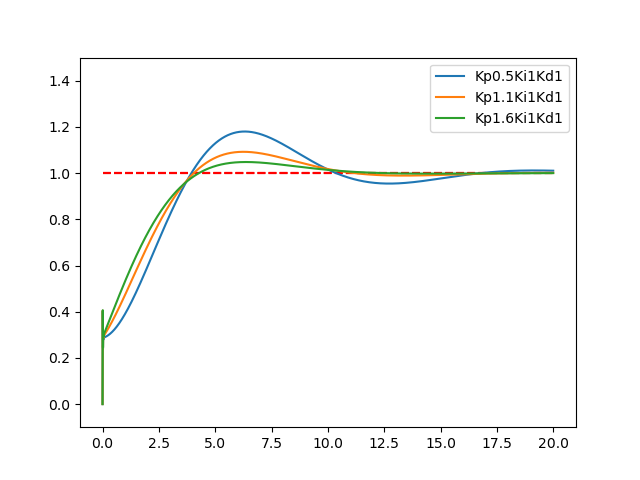
一方、Kp依存性は以下のように描け、どうもまだまだパラメータを選ばないと再現できていません。

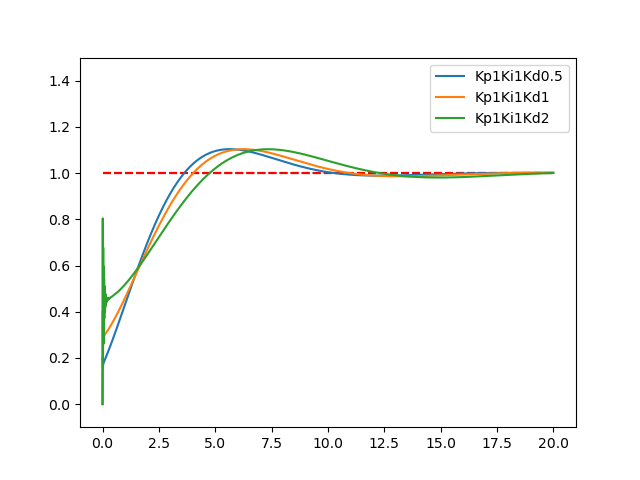
そして、Kd依存性は以下のとおり、ほぼ再現しているように見えます。

###制御対象について
今回は、電気炉の温度をイメージして制御対象を設定しました。実際の制御ではもっと動的なものを制御する必要があります。
その場合は、今回導入したufunc()を書き換えることによって実現できるものと思います。
また、制御対象によっては、PID制御できない対象もあると思います。
そのあたりについての限界については、さらに追及していく必要があります。
###まとめ
・PID制御して遊んでみた
・ジーグラ・ニコルスの限界感度法で制御パラメターを決定した
・Wikipediaの掲載グラフを再現してみた
・制御対象を記述する関数を陽に定義できた
・サンプリング時間dtを導入した

・実際に、温調やモーター制御などに応用したいと思う