【シミュレーション入門】サイン波のマスゲーム♬

今回もハマった。
Twitterで流れてきた、以下の振り子。
Wonder of Science@wonderofscienceさん

それぞれ独立なので、集団運動に見える。しかも、あのポアンカレの再帰定理を思い起こさせるような動き。
「力学系は、ある種の条件が満たされれば、その任意の初期状態に有限時間内にほぼ回帰する」
まあ、今回は単純な単振り子なので、周期さえコントロールすれば当たり前。。。なのだが、そんなに簡単ではないと直感的には感じた。

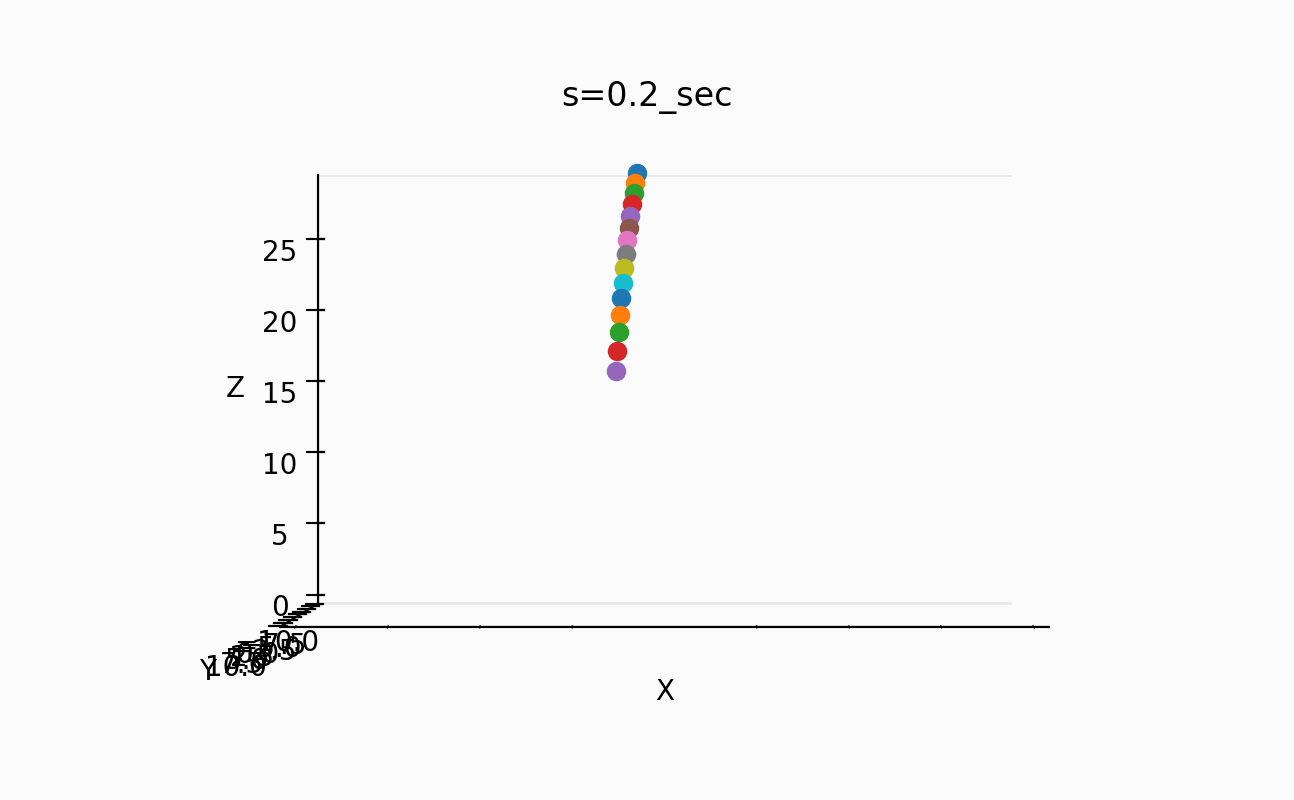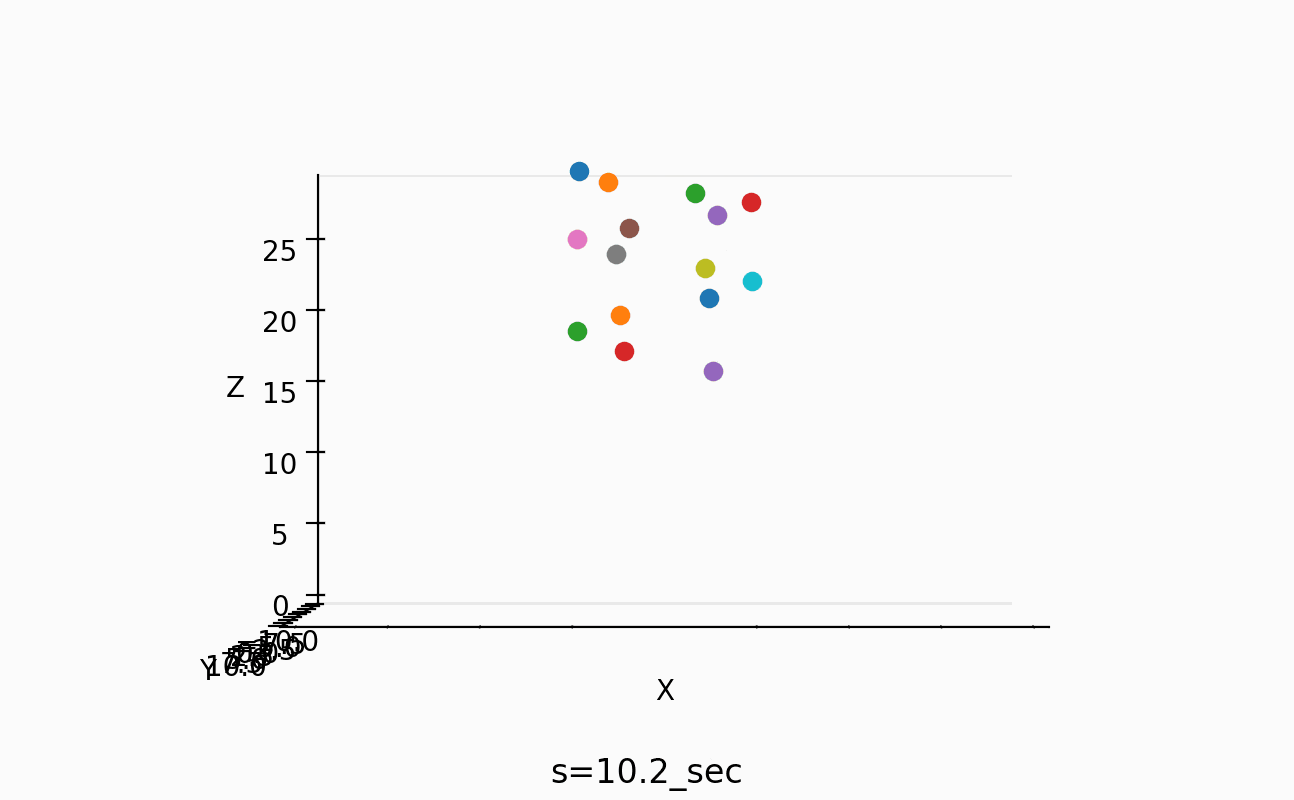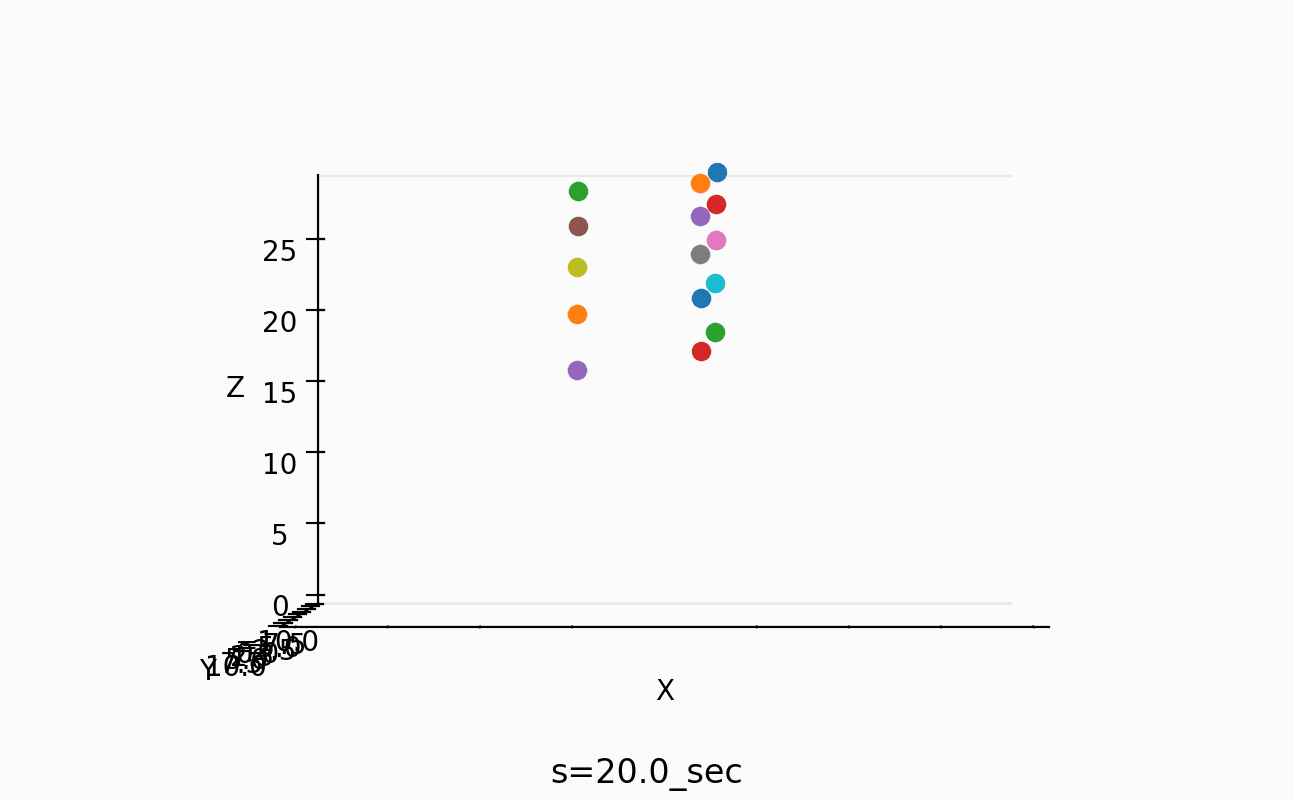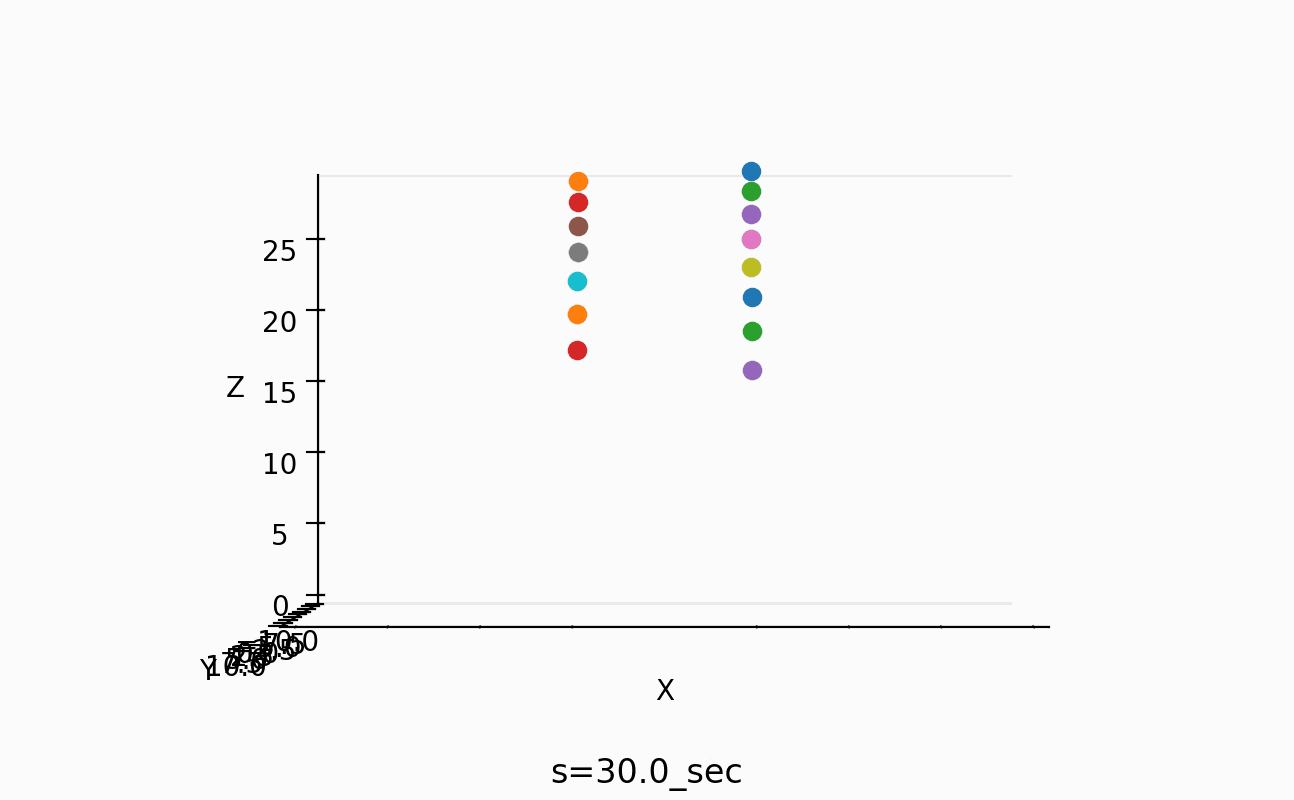
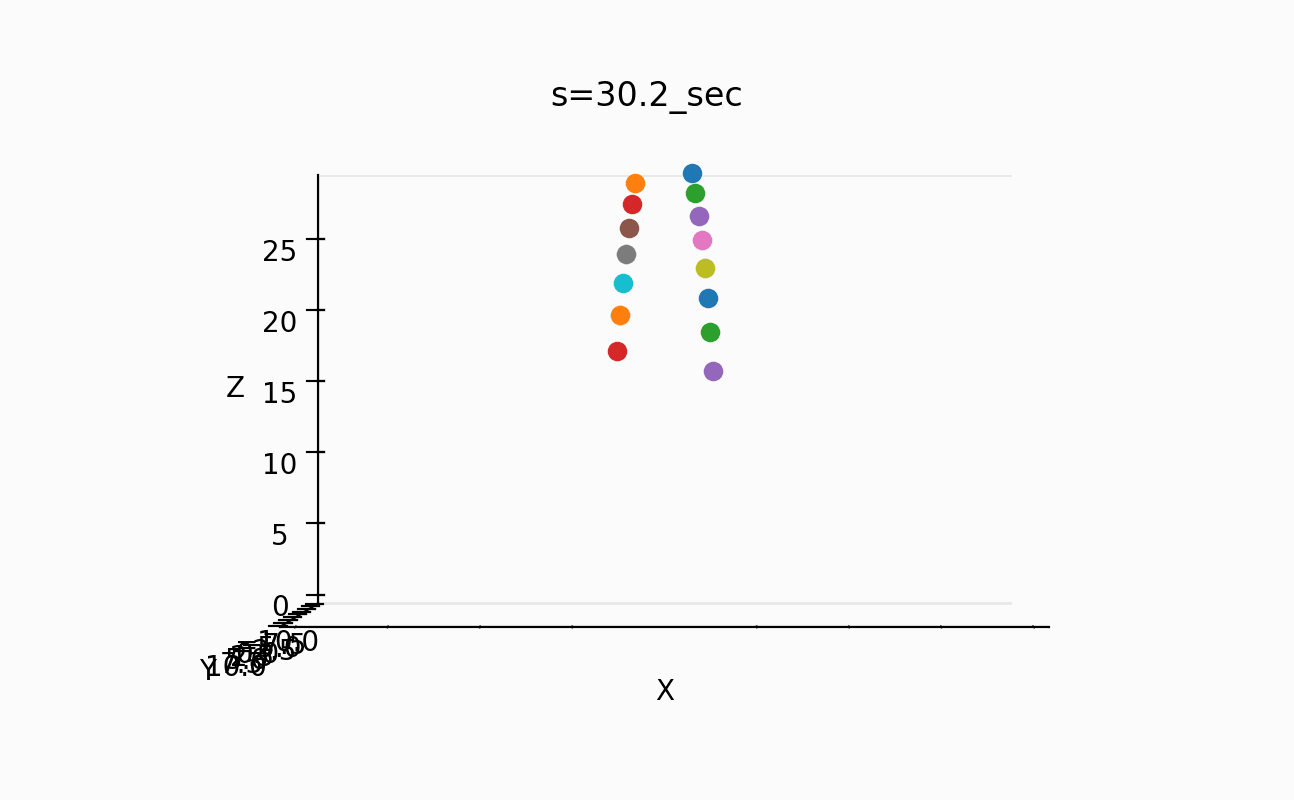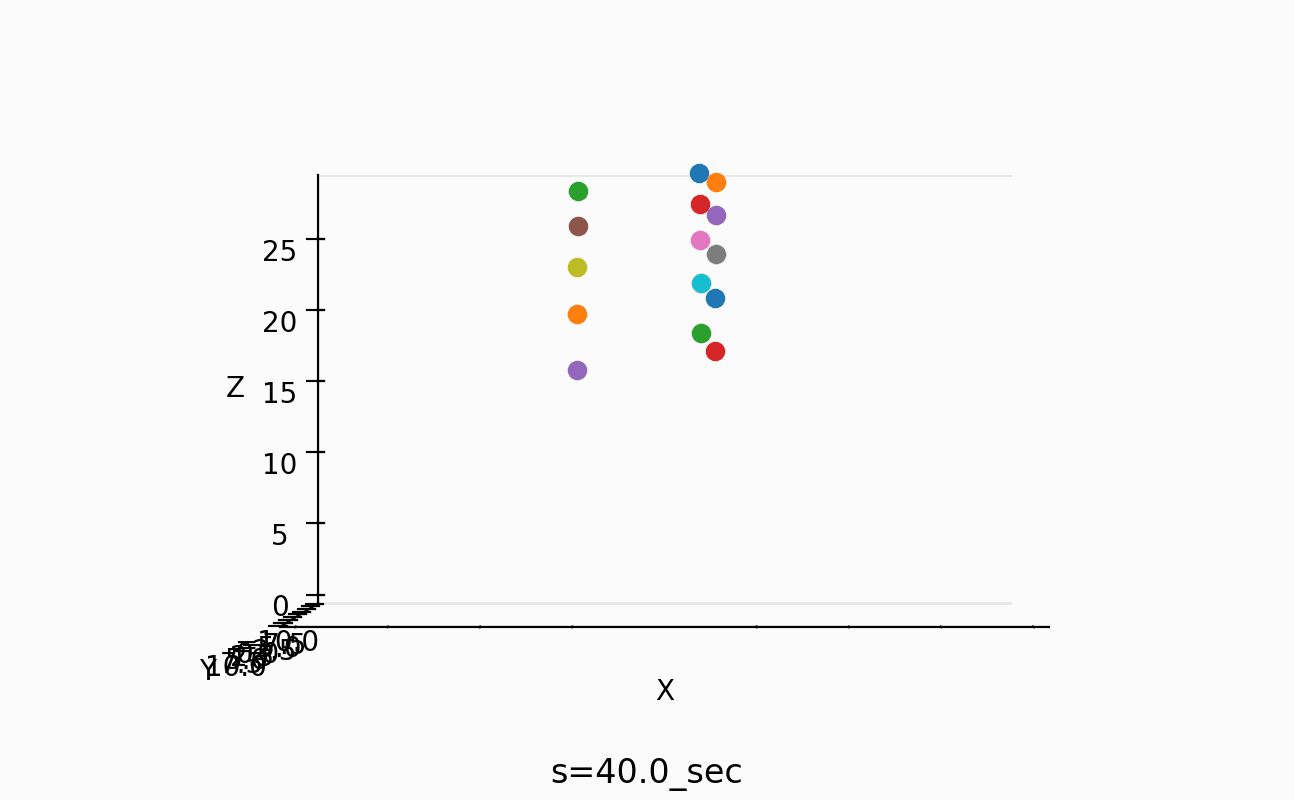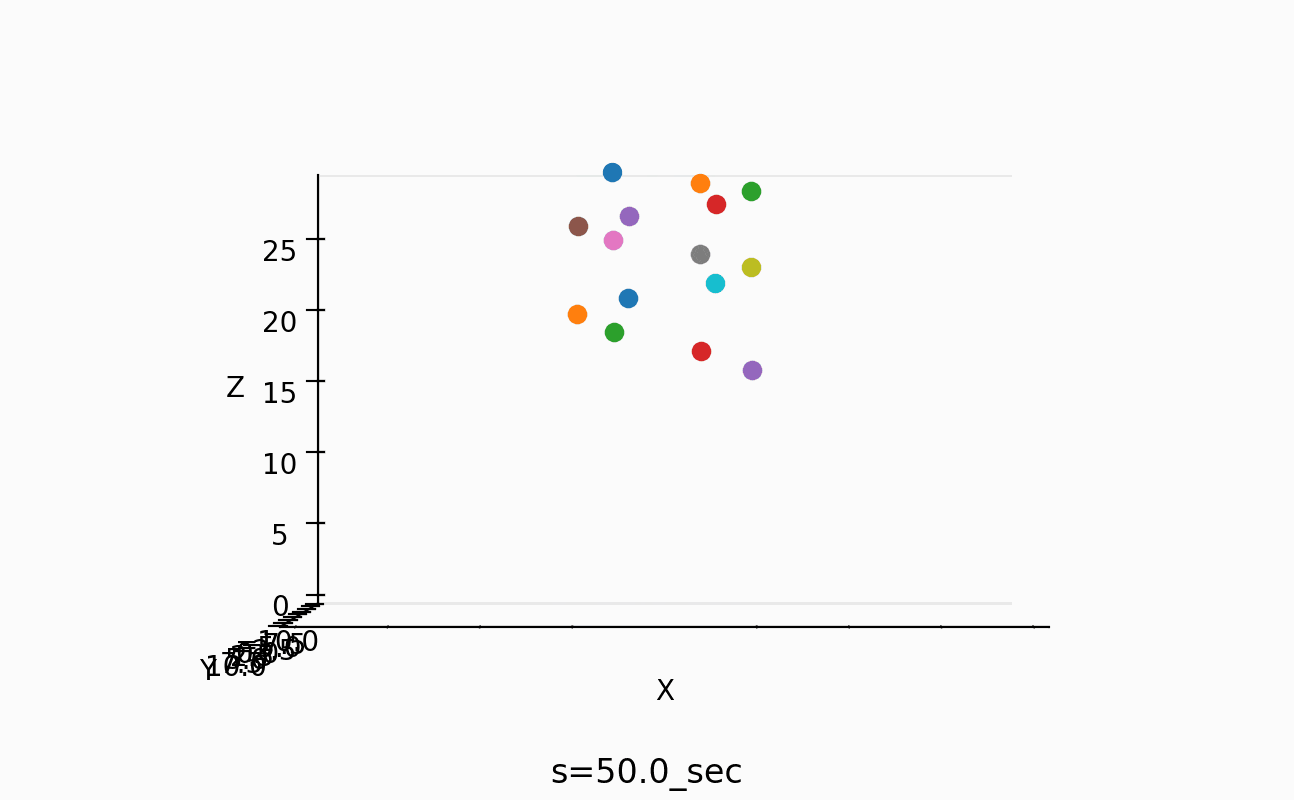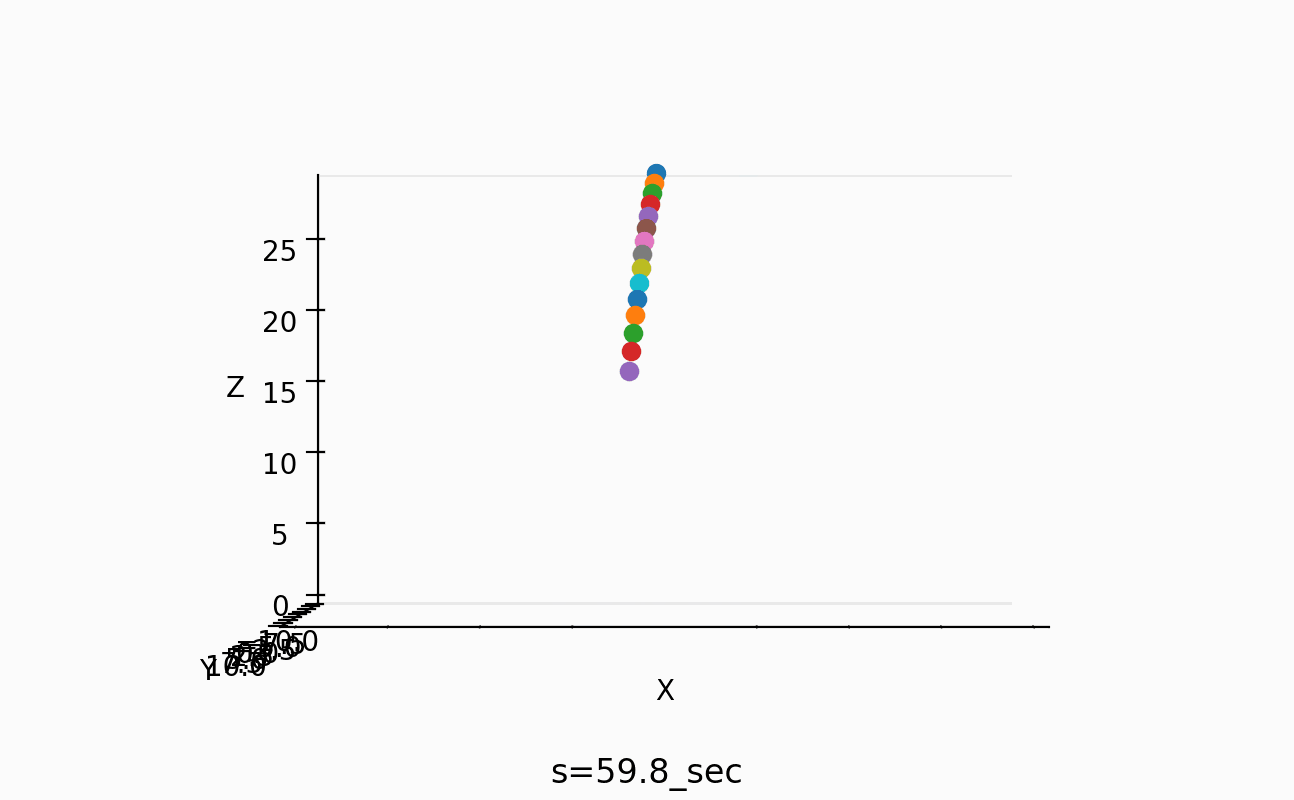
以下のようなスナップも取ってみた。
一番短い振り子の周期は、約1秒なのが分かるし、一番長い振り子の周期は約4／3倍の周期のようだ。

しかし、この情報だけでは、間の振り子の周期をどうすればあのように綺麗にそろうのかが不明でした。
散々悩んでいろいろやった後、参考の元ネタを読んだ。最初から元ネタへのリンクが張ってあったんだけど、この時に限って読んでいませんでした。
【参考】元ネタ
Pendulum Waves@Harvard Natural Sciences Lecture Demonstrations
ネ・タ・バ・レ。
「ダンスの完全な1サイクルの期間は60秒です。最長の振り子の長さは、この60秒間に51回振動するように調整されています。連続する短い振り子の長さは、この期間にさらに1つの振動を実行するように注意深く調整されます。したがって、15番目の振り子（最短）は65回振動します。 15のすべての振り子が一緒に開始されると、それらはすぐに同期から外れます。相対振動の周期が異なるため、相対位相は連続的に変化します。ただし、60秒後、それらはすべて整数倍の振動を実行し、その瞬間に再び同期し、ダンスを繰り返す準備ができます。」

もちろん、これを参考のように本物の振り子で実現するのはかなり大変だろう。しかし、ここではシミュレーションしてしまおうということで、さらにいろいろ試してみようと思う。
【参考】
蛇振り子@アマゾン

###単振り子のおさらい
【参考】
解説：　単振り子の運動
微分方程式の数値解でもいいけど、ここは以下の解析解を使うこととしました。

\theta = \theta_0\sin(\omega t+\delta)  \\
\omega = \sqrt{\frac{g}{L}}\\
T=\frac{2\pi}{\omega}\\
\theta = \theta_0\sin(\frac{2\pi t}{T}+\delta)  \\
T;sec \\ t; sec\\
L=\frac{g}{\omega ^2}=g(\frac{T}{2\pi})^2\\
g=980 cm/s^2\\
L=24.82 cmのとき、\\
T=1.000sec

上のネタバレを表にすると以下のとおり

n	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
T	60/65=0.923	60/64	60/63	60/62	60/61	60/60	60/59	60/58	60/57	60/56	60/55	60/54	60/53	60/52	60/51=1.176
L	$L_0=21.15$	$L_0(65/64)^2$	$L_0(65/63)^2$	$L_0(65/62)^2$	...	...	...	...	...	...	...	...	...	$L_0(65/52)^2$	$L_{14}=34.36$
$T_n/T_{n-1}$	-	65/64	64/63	63/62	62/61	61/60	60/59	59/58	58/57	57/56	56/55	55/54	54/53	53/52	52/51
###コード解説
コードはおまけに全体を置きました。
先日のAxes3Dのアニメーションとほぼ同様です。
肝心な部分は、以下のとおりです。

def genxy(n,L=20,z0=0):
    phi = 0  #時間初期値
    g = 980  #重力加速度
    x0=2.5  #振幅初期値
    omega = np.sqrt(g/L)
    theta0 = np.arcsin(x0/L)  #初期角度
    while phi < 600:  #最大振幅から開始のためpi/2を追加
        yield np.array([L*np.sin(np.sin(phi*omega+np.pi/2)*theta0), 0,z0-L+L*(1-np.cos(np.sin(phi*omega+np.pi/2)*theta0))])
        phi += 1/n  #1secをn分割する

これを、以下のコードで呼び出して利用します
ここで、N=60,Lは、それぞれの振り子の長さです。z0は支点の高さです。
datazを計算して、それをlinezでプロットします。

dataz = np.array(list(genxy(N,L=L0*Fc[0]**2,z0=z0))).T
linez, = ax.plot(dataz[0, 0:1], dataz[1, 0:1], dataz[2, 0:1],'o')

これを、以下のupdate関数で逐次numで指定して表示します。

def update(num, data, line,s):
    line.set_data(data[:2,num-1 :num])
    line.set_3d_properties(data[2,num-1 :num])
    ax.set_xticklabels([])
    ax.grid(False)

今回は二次元でも同じ絵が得られますが、振り子をよりリアルに（y方向に並べたりして）、ぐりぐりマウスで回せるので、一応3dプロットで描いています。
そして、一番肝心なLの計算は上の表を参考にして以下で実施しました。
これから計算できるFcを利用して、それぞれの振り子の長さは$L=L_0*F_c[i]**2$で計算できます。

L0=980*(60/65)**2/(2*np.pi)**2
Fc=[]
fc=1
Fc.append(fc)
for i in range(1,15,1):
    fc=fc*((66-i)/(65-i))
    Fc.append(fc)

###再現；15個の振り子
0.2-30 sec

30.2-60 sec

###拡大；30個の振り子
倍の数でやってみた。
0.2-30 sec

30.2-60 sec

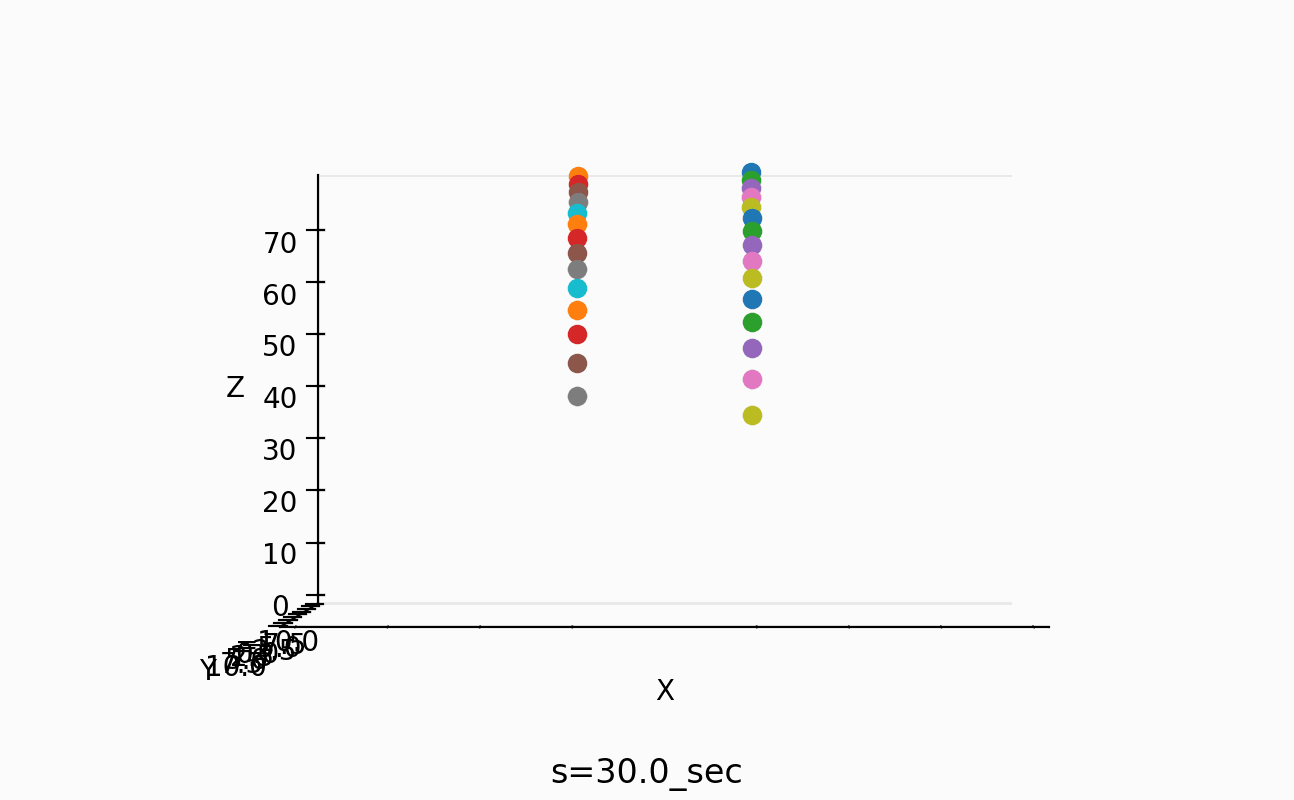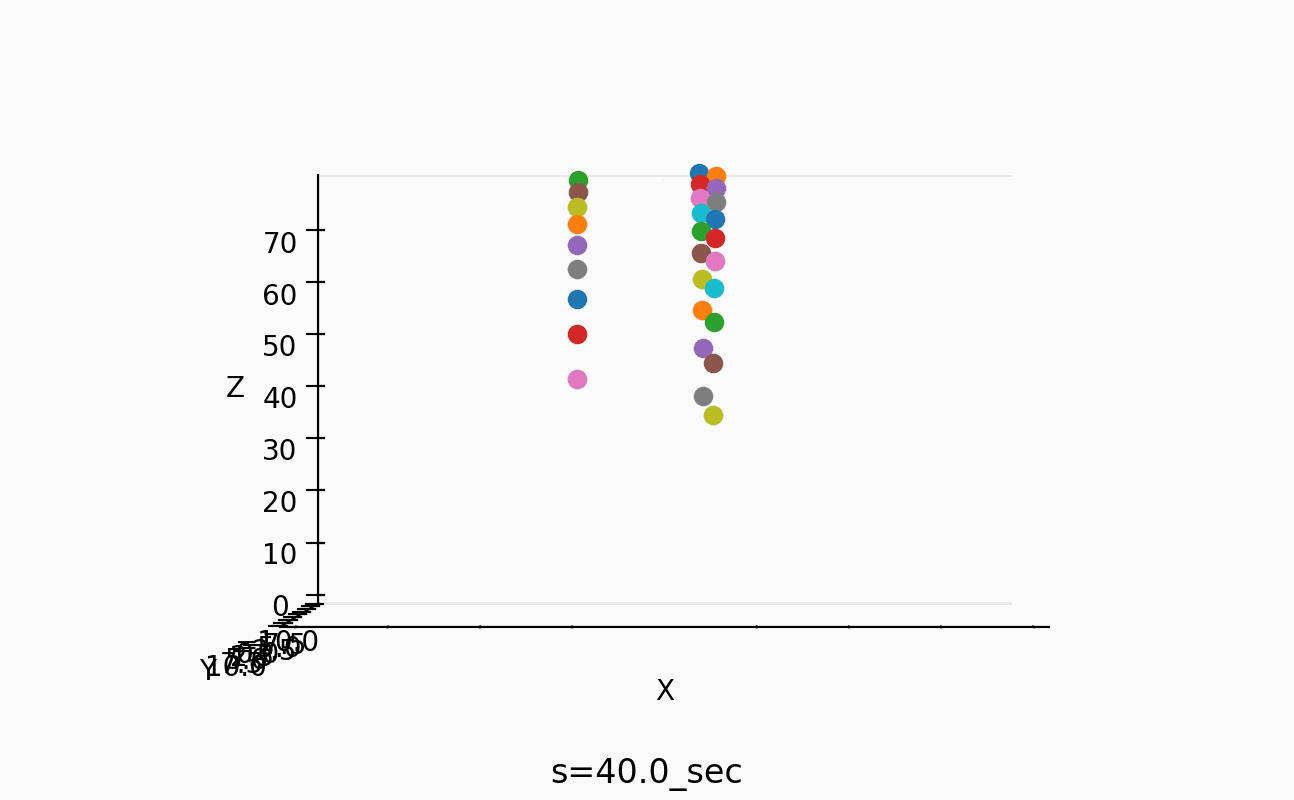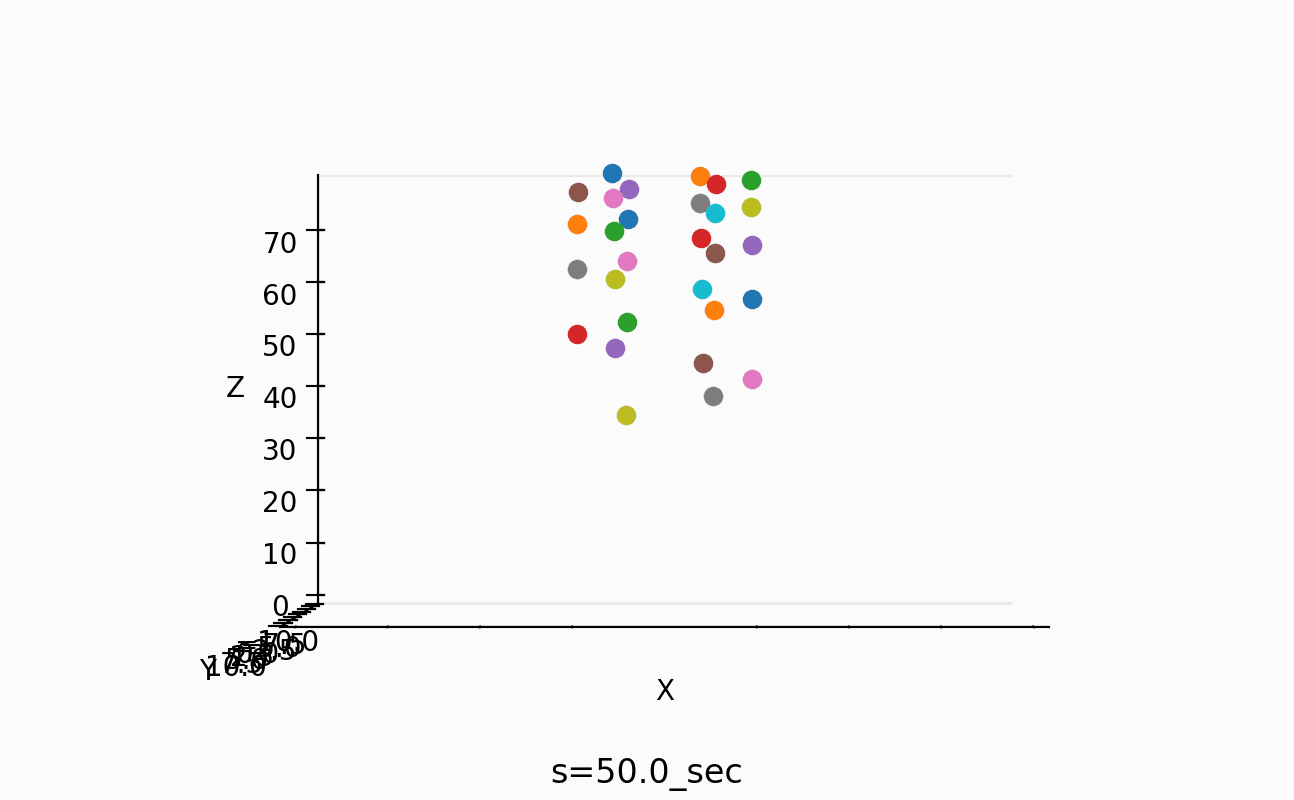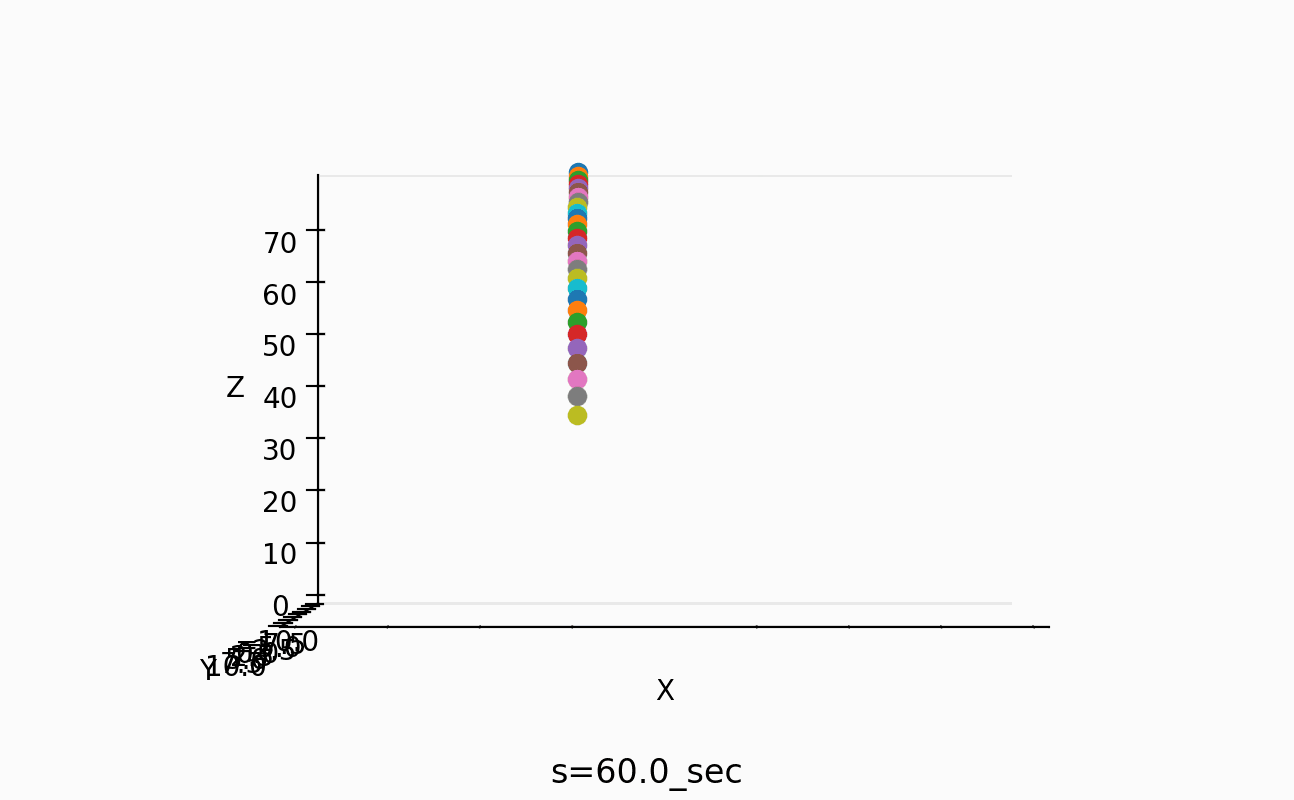
###ちょっと議論
出来ちゃうと、なーんだだけど、実際ゼロからコード書くと悩むと思います。
こんなに綺麗に勢ぞろいさせられるのかという不思議感がなかなか抜けません。
そして、実は個数は3個から順に増やしてみました。少ないときも同じように動くのが面白いです。もちろんこの方式だと、上のLを求めるためのFcの計算が出来るところまでは、同じように計算できます。
そして、さらに増やしたければ、60秒でそろう部分を変更すれば、さらに異なるバリエーションができます。ということで、50個に挑戦してみました。
まず、リスト使ってdataz, linezを簡単にfor文で計算できるようにしました。

dataz=[]
linez=[]
for j in range(50):
    dataz0 = np.array(list(genxy(N,L=L0*Fc[j]**2,z0=z0))).T
    linez0, = ax.plot(dataz0[0, 0:1], dataz0[1, 0:1], dataz0[2, 0:1],'o')
    dataz.append(dataz0)
    linez.append(linez0)

表示する部分も以下のように簡素化しています。

    for j in range(50):        
        update(num,dataz[j],linez[j],s0)

これで、50個の場合は、以下のように3mにもなるんですね。


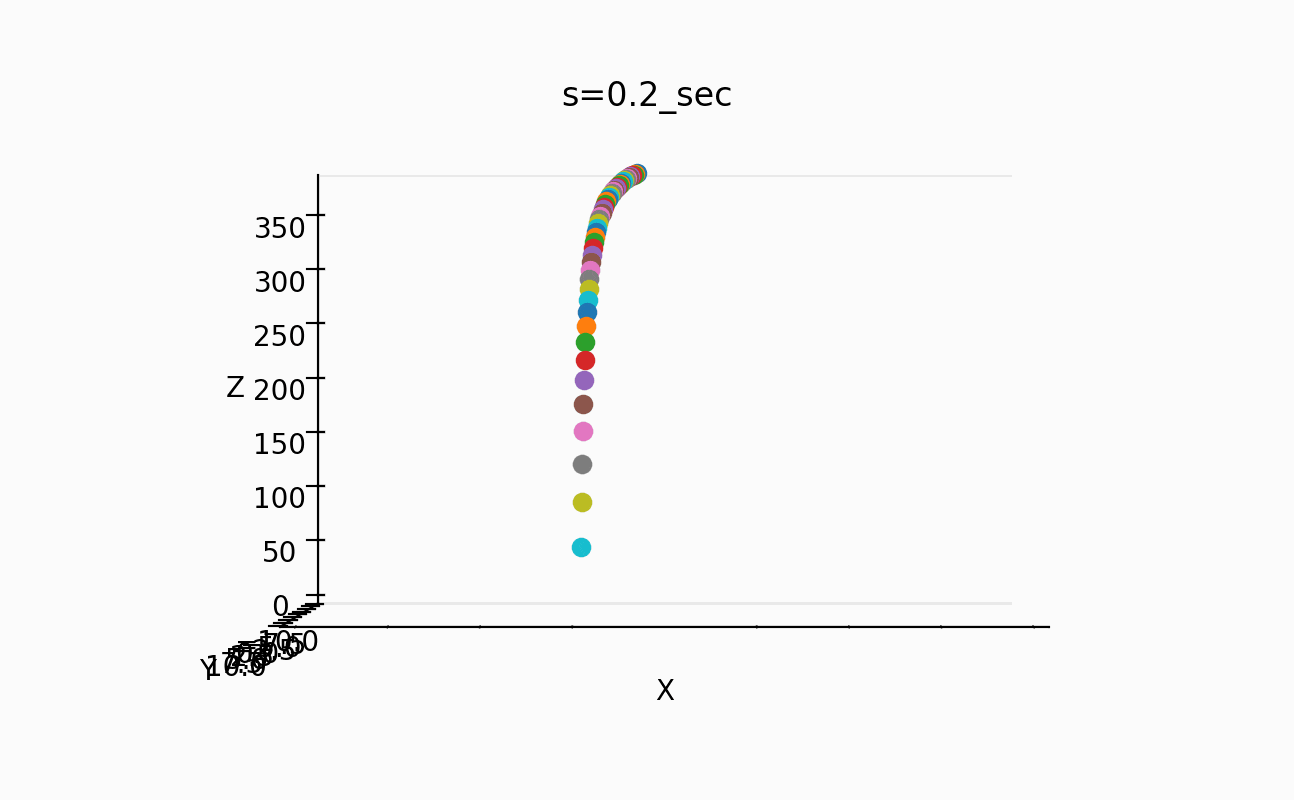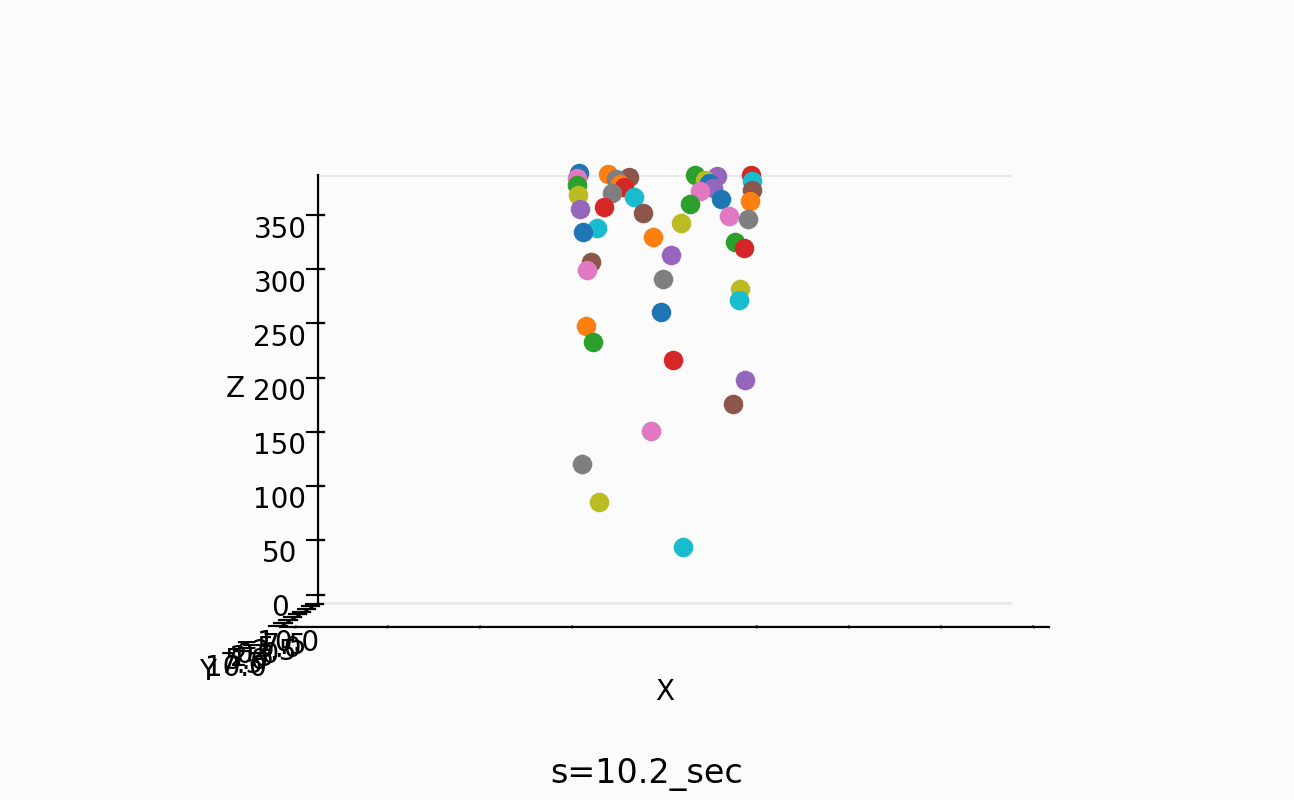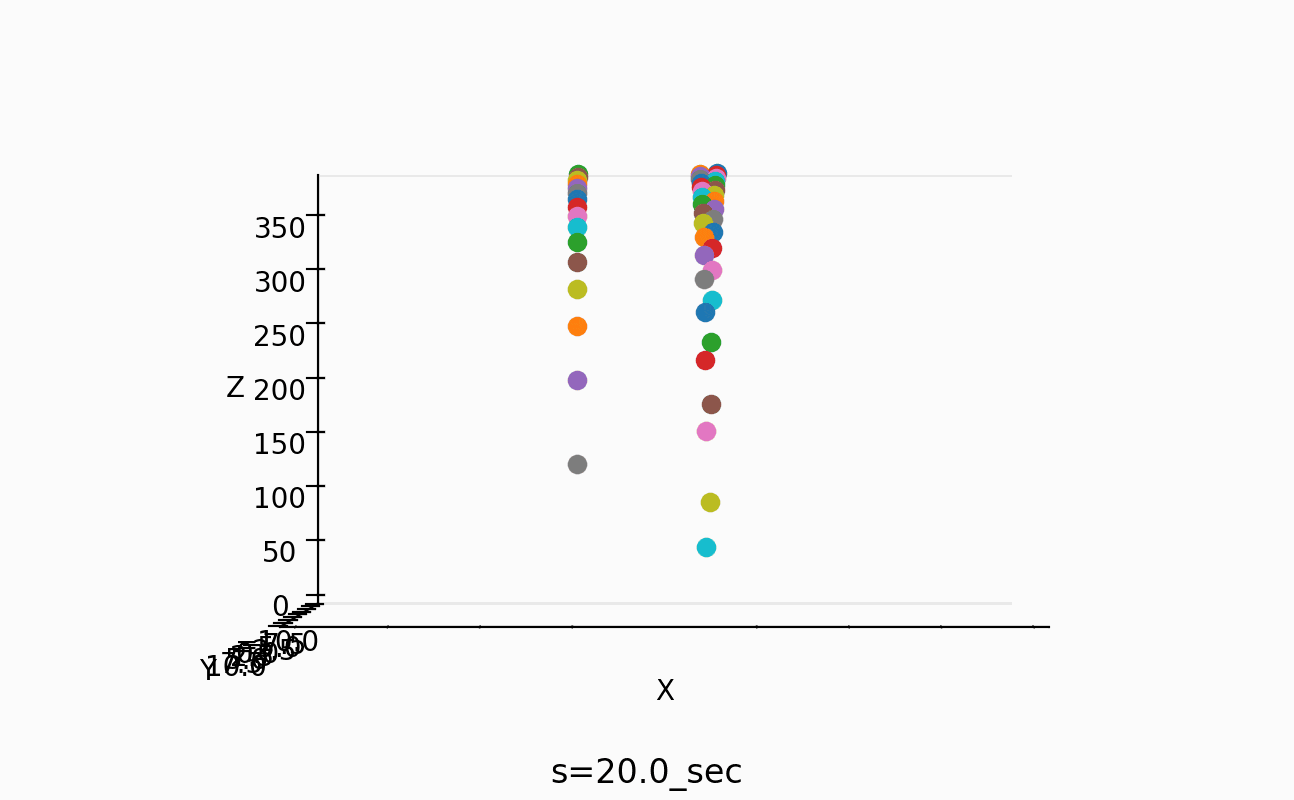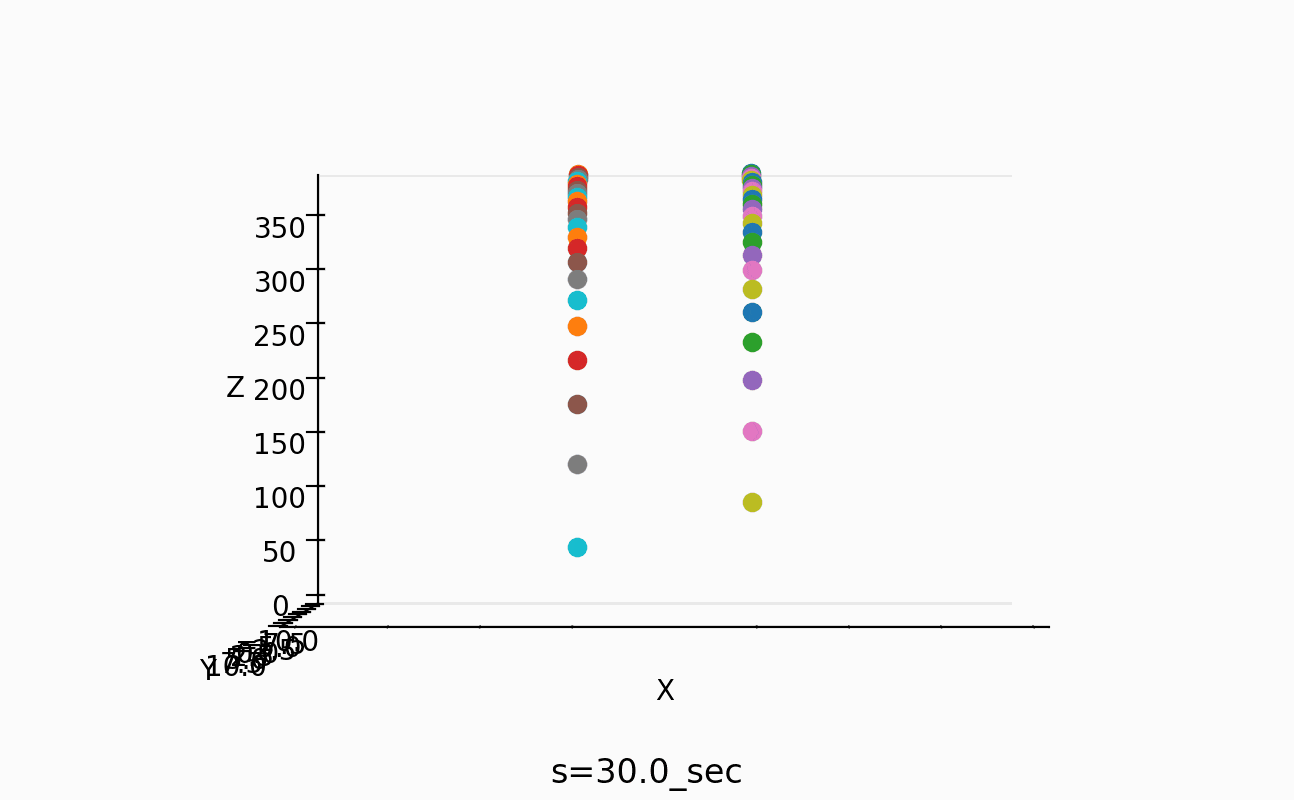
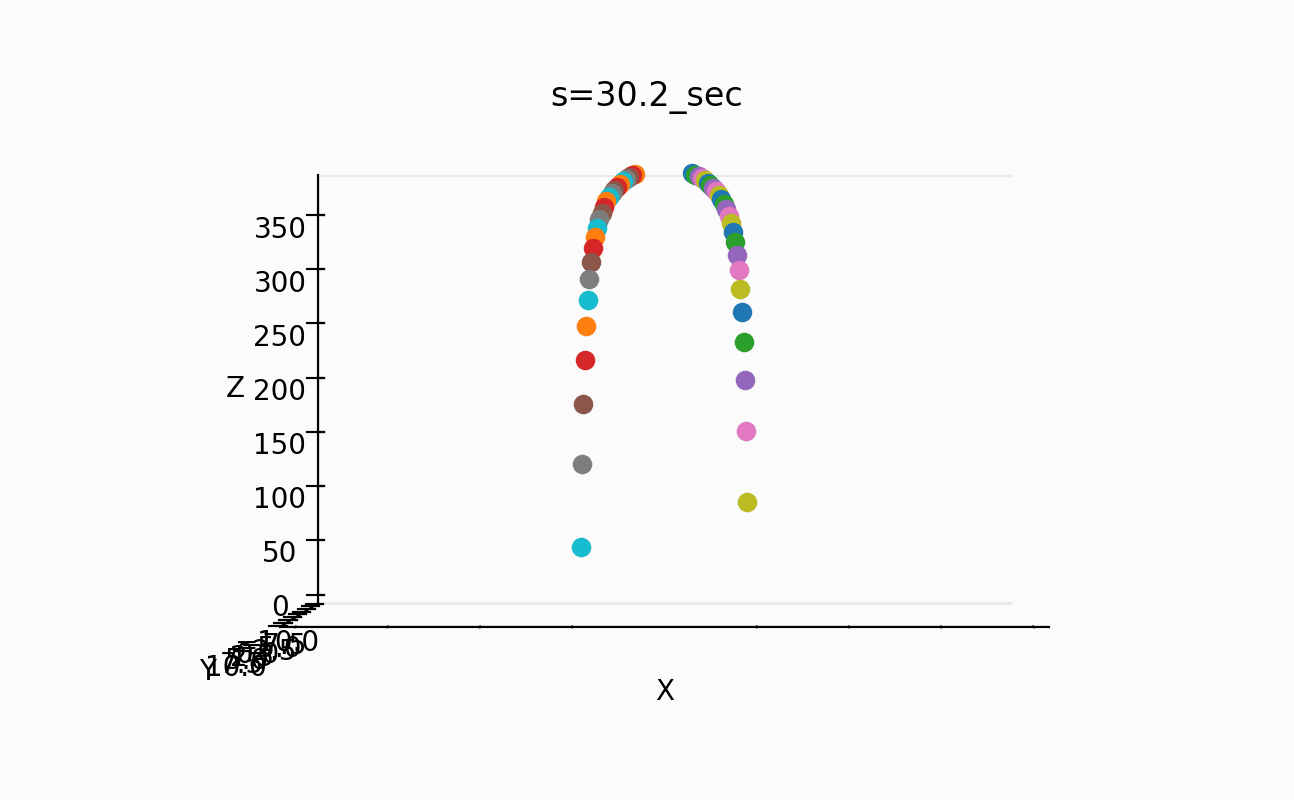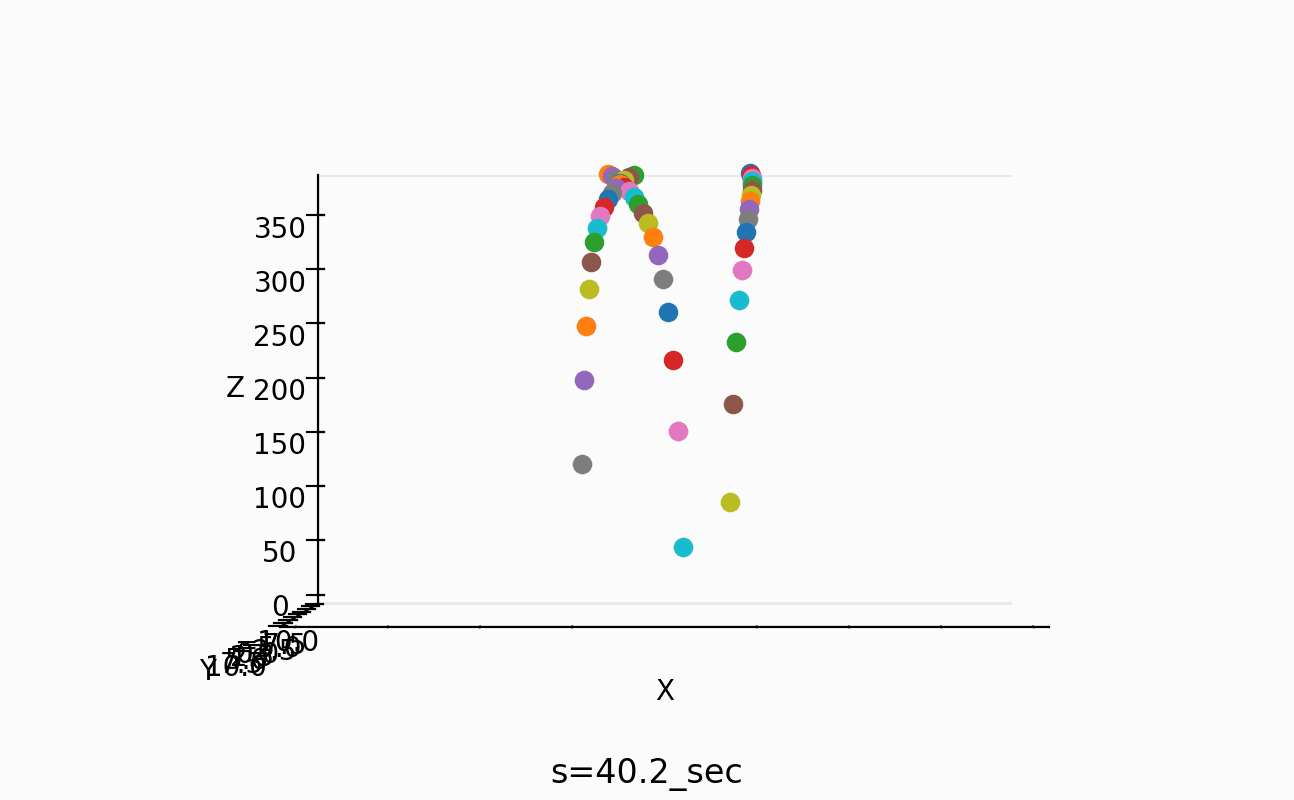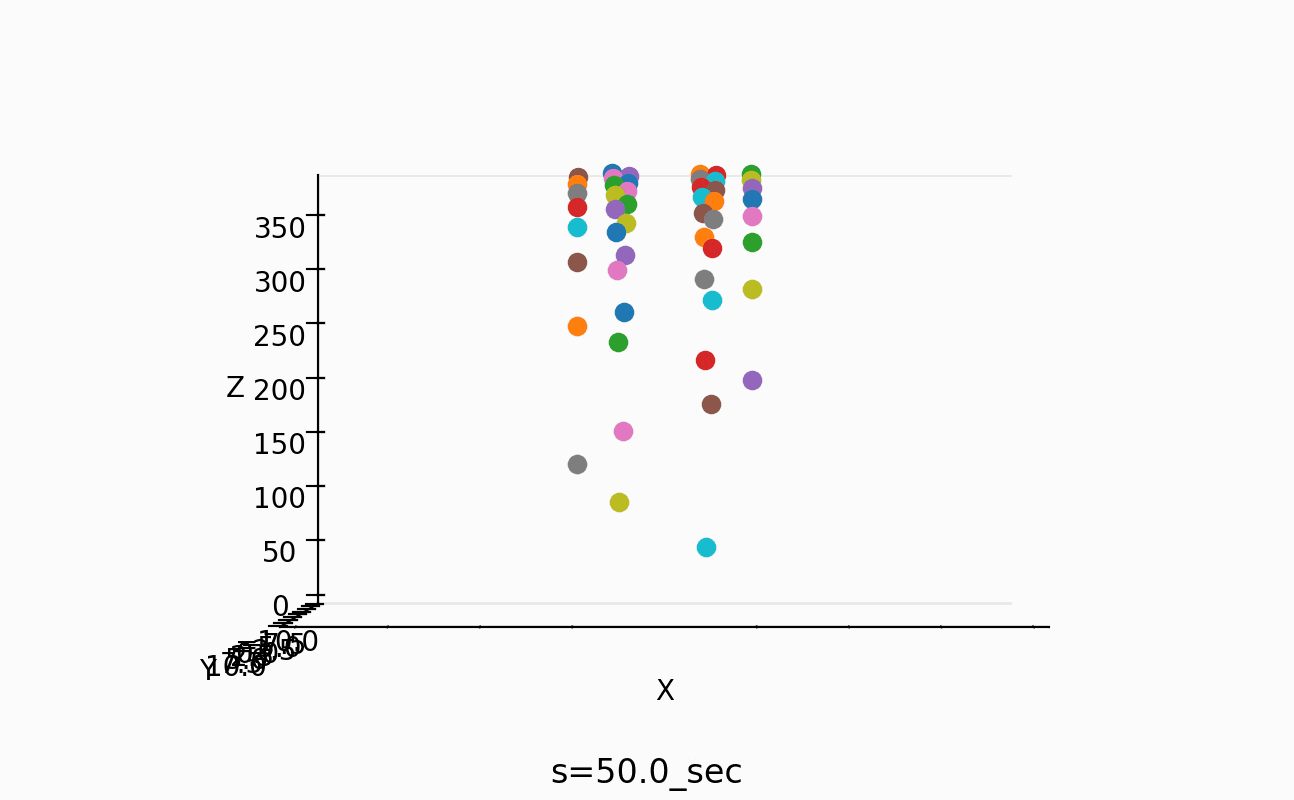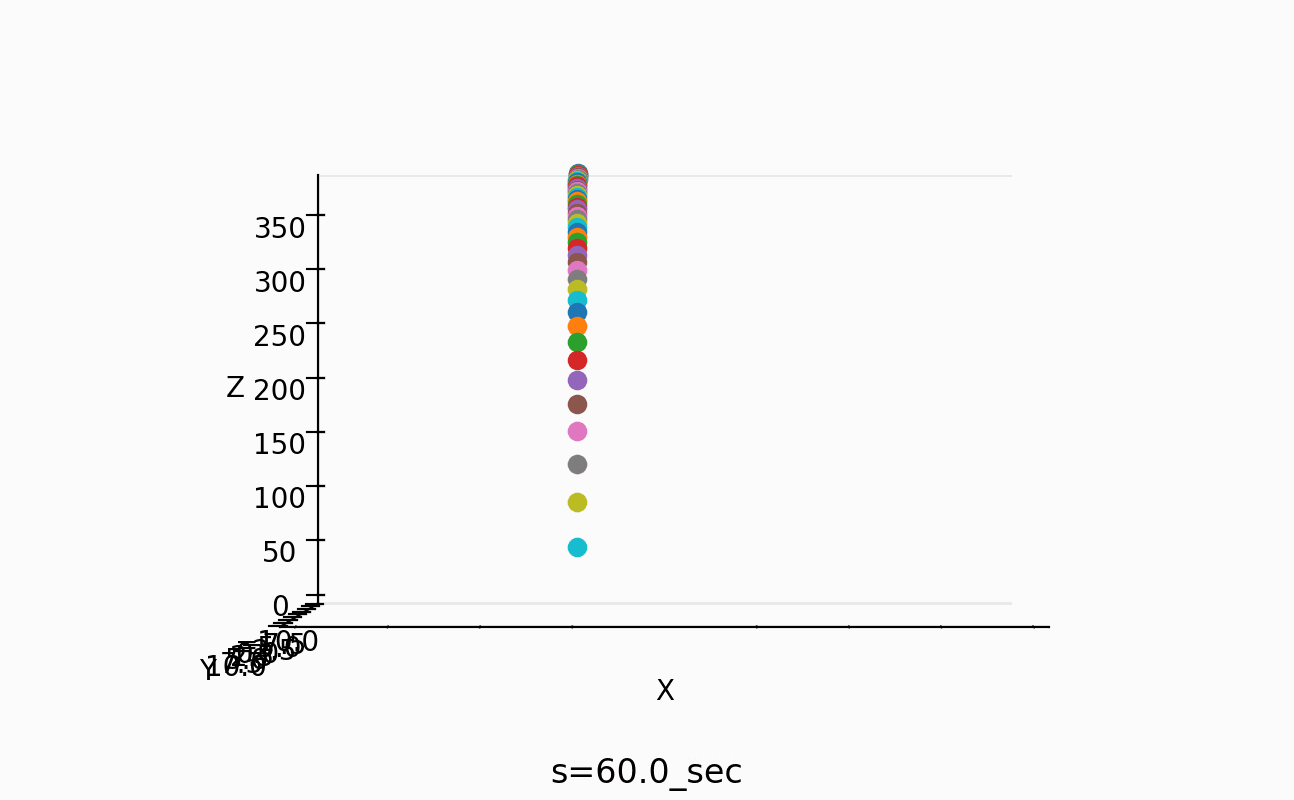
これは、これで作ってみたくなります。

###まとめ
・サイン波のマスゲームをシミュレーションしてみた
・単純なものだが、美しく動く

・いろいろな拡張が出来そうで楽しみ
・本物も動かしたくなった
###おまけ

from matplotlib import pyplot as plt
import numpy as np
import mpl_toolkits.mplot3d.axes3d as p3
from matplotlib import animation

fig, ax = plt.subplots(1,1,figsize=(1.6180 * 4, 4*1),dpi=200)
ax = p3.Axes3D(fig)

def genxy(n,L=20,z0=0):
    phi = 0  #時間初期値
    g = 980  #重力加速度
    x0=2.5  #振幅初期値
    omega = np.sqrt(g/L)
    theta0 = np.arcsin(x0/L)  #初期角度
    while phi < 600:  #最大振幅から開始のためpi/2を追加
        yield np.array([L*np.sin(np.sin(phi*omega+np.pi/2)*theta0), 0,z0-L+L*(1-np.cos(np.sin(phi*omega+np.pi/2)*theta0))])
        phi += 1/n  #1secをn分割する

def update(num, data, line,s):
    line.set_data(data[:2,num-1 :num])
    line.set_3d_properties(data[2,num-1 :num])
    ax.set_xticklabels([])
    ax.grid(False)
    
N = 360
z0 =50
L0=980*(60/65)**2/(2*np.pi)**2
Fc=[]
fc=1
Fc.append(fc)
for i in range(1,15,1):
    fc=fc*((66-i)/(65-i))
    Fc.append(fc)

dataz=[]
linez=[]
for j in range(50):
    dataz0 = np.array(list(genxy(N,L=L0*Fc[j]**2,z0=z0))).T
    linez0, = ax.plot(dataz0[0, 0:1], dataz0[1, 0:1], dataz0[2, 0:1],'o')
    dataz.append(dataz0)
    linez.append(linez0)

# Setting the axes properties
ax.set_xlim3d([-10., 10])
ax.set_xlabel('X')

ax.set_ylim3d([-10.0, 10.0])
ax.set_ylabel('Y')

ax.set_zlim3d([0.0, z0-L0])
ax.set_zlabel('Z')
elev=0
azim=90
ax.view_init(elev, azim)

frames =30*60
fr0=60
s0=30*60
s=s0
while 1:
    s+=1
    num = s
    for j in range(50):        
        update(num,dataz[j],linez[j],s0)
 
    if s%fr0==0:
        print(s/fr0)
    plt.pause(0.001)