昨夜は、【データサイエンティスト入門】科学計算、データ加工、グラフ描画ライブラリの使い方の基礎として環境構築の話をしましたが、今夜はNumpyの基礎をまとめます。
【注意】
「東京大学のデータサイエンティスト育成講座」を読んで、ちょっと疑問を持ったところや有用だと感じた部分をまとめて行こうと思う。
したがって、あらすじはまんまになると思うが内容は本書とは関係ないと思って読んでいただきたい。
Chapter 2-2 Numpyの基礎
本書より引用
「Numpyは、科学計算で最もよく使われる基本的なライブラリです。...PythonではなくC言語で書かれたモジュールであり、処理が高速なのも特徴です。」
この後、ちょっと本書を離れて、参考のNumpy.orgのTutorialをトレースします。翻訳文は「」で示します。
なお、一通り写経するのにほぼ3日かかった。
【参考】
・Quickstart tutorial
基本
「NumPyの主なオブジェクトは同種の多次元配列です。これは、要素(通常は数値)のテーブルであり、すべて同じ型であり、負でない整数のタプルによってインデックスが付けられます。 NumPyでは、次元は軸と呼ばれます。」
「たとえば、3D空間内の点の座標[1、2、1]には1つの軸があります。その軸には3つの要素があるため、長さは3です。下の例では、配列に2つの軸があります。最初の軸の長さは2で、2番目の軸の長さは3です。」
[[ 1., 0., 0.],
[ 0., 1., 2.]]
「NumPyの配列クラスは、ndarrayと呼ばれます。...ndarrayオブジェクトの重要な属性は: 」
| ndarrayオブジェクトの属性 | 説明 |
|---|---|
| ndarray.ndim | 配列の軸の数;次元数 |
| ndarray.shape | 配列の次元。各次元の配列のサイズを示す整数のタプル。 n行m列の行列の場合、形状は(n、m) |
| ndarray.size | 配列の要素の総数。形状の要素の積に等しい。 |
| ndarray.dtype | 配列の要素のタイプ |
| ndarray.itemsize | 配列の各要素のサイズ(バイト単位)。 |
| ndarray.data | 配列の実際の要素を含むバッファ。余り使われない |
Numpyライブラリを読込み、上記の属性を出力してみます。
例
>>> import numpy as np
>>> a = np.arange(15).reshape(3, 5)
>>> a
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
>>> a.ndim
2
>>> a.shape
(3, 5)
>>> a.size
15
>>> a.dtype
dtype('int32')
>>> a.itemsize
4
>>> a.data
<memory at 0x0000020DC66C8C18>
>>> type(a)
<class 'numpy.ndarray'>
配列生成
>>> a = np.array([2,3,4])
>>> a
array([2, 3, 4])
>>> a.dtype
dtype('int32')
>>> b = np.array([1.2, 3.5, 5.1])
>>> b
array([1.2, 3.5, 5.1])
>>> b.dtype
dtype('float64')
以下はエラーと正しい例
>>> a = np.array(1,2,3,4) #エラー
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: only 2 non-keyword arguments accepted
>>> a = np.array([1,2,3,4]) #正しい
>>> a
array([1, 2, 3, 4])
「arrayは、シーケンスのシーケンスを2次元アレイに変換する。」
>>> b = np.array([(1.5,2,3), (4,5,6)])
>>> b
array([[1.5, 2. , 3. ],
[4. , 5. , 6. ]])
>>> b.ndim
2
>>> b.itemsize
8
「配列のタイプは、作成時に明示的に指定することもできる。」
>>> c = np.array( [ [1,2], [3,4] ], dtype=complex )
>>> c
array([[1.+0.j, 2.+0.j],
[3.+0.j, 4.+0.j]])
>>> c.ndim
2
>>> c.itemsize
16
>>> np.zeros((3, 4))
array([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
>>> np.ones( (2,3,4), dtype=np.int16 )
array([[[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1]],
[[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1]]], dtype=int16)
>>> np.empty( (2,3) )
array([[1.5, 2. , 3. ],
[4. , 5. , 6. ]])
結果
emptyは、上のbの結果が入る。
最初からやり直すと、思惑通りの結果が得られ、上の事象も再現された。
>python
>>> import numpy as np
>>> np.empty( (2,3) )
array([[4.89543071e-307, 2.33646845e-307, 3.22646744e-307],
[7.56569929e-307, 9.34575838e-307, 4.22792892e-307]])
>>> b = np.array([(1.5,2,3), (4,5,6)])
>>> b
array([[1.5, 2. , 3. ],
[4. , 5. , 6. ]])
>>> np.arange( 10, 30, 5 ) #10-30まで5おきに生成30は除く
array([10, 15, 20, 25])
>>> np.arange( 0, 2, 0.3 ) #0-2まで0.3おきに生成
array([0. , 0.3, 0.6, 0.9, 1.2, 1.5, 1.8])
配列出力
「配列を出力すると、NumPyは配列をネストされたリストと同じように表示しますが、次のレイアウトになります。
・最後の軸は左から右に印刷され、
・最後から2番目が上から下に印刷され、
・残りも上から下に印刷され、各スライスは空の行で次のスライスと区切られます。
1次元配列は行として、2次元は行列として、3次元は行列のリストとして出力されます。」
>>> a = np.arange(6) # 1d array
>>> print(a)
[0 1 2 3 4 5]
>>> b = np.arange(12).reshape(4,3) # 2d array
>>> print(b)
[[ 0 1 2] #最後の軸は左から右に印刷
[ 3 4 5] #最後から2番目が上から下に印刷
[ 6 7 8]
[ 9 10 11]]
>>> c = np.arange(24).reshape(2,3,4) # 3d array
>>> print(c)
[[[ 0 1 2 3] #残りも上から下に印刷
[ 4 5 6 7]
[ 8 9 10 11]]
#各スライスは空の行で次のスライスと区切られ
[[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]]
「配列が大きすぎて印刷できない場合、NumPyは自動的に配列の中央部分をスキップし、コーナーのみを印刷します。」
>>> print(np.arange(10000))
[ 0 1 2 ... 9997 9998 9999]
>>> print(np.arange(10000).reshape(100,100))
[[ 0 1 2 ... 97 98 99]
[ 100 101 102 ... 197 198 199]
[ 200 201 202 ... 297 298 299]
...
[9700 9701 9702 ... 9797 9798 9799]
[9800 9801 9802 ... 9897 9898 9899]
[9900 9901 9902 ... 9997 9998 9999]]
上の機能を止めて、全部の要素を出力したいとき。
np.set_printoptions(threshold=sys.maxsize)
>>> print(np.arange(10000))
[ 0 1 2 ... 9997 9998 9999]
>>> import sys
>>> np.set_printoptions(threshold=sys.maxsize)
>>> print(np.arange(10000))
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13
14 15 16 17 18 19 20 21 22 23 24 25 26 27
...
9982 9983 9984 9985 9986 9987 9988 9989 9990 9991 9992 9993 9994 9995
9996 9997 9998 9999]
基本的演算
>>> a = np.array( [20,30,40,50] )
>>> b = np.arange( 4 )
>>> b
array([0, 1, 2, 3])
>>> c = a-b
>>> c
array([20, 29, 38, 47])
>>> b**2
array([0, 1, 4, 9], dtype=int32)
>>> 10*np.sin(a)
array([ 9.12945251, -9.88031624, 7.4511316 , -2.62374854])
>>> a<35
array([ True, True, False, False])
「多くの行列言語とは異なり、積演算子*はNumPy配列で要素ごとに動作します。
行列積は、@演算子(Python> = 3.5の場合)またはドット関数またはドットメソッドを使用して実行できます。」
要素ごとの積
行列の積
>>> A = np.array( [[1,1],[0,1]] )
>>> B = np.array( [[2,0],[3,4]] )
>>> A*B # elementwise product 要素毎の積
array([[2, 0],
[0, 4]])
>>> A @ B # matrix product 行列の積
array([[5, 4],
[3, 4]])
>>> A.dot(B) # another matrix product 行列の積
array([[5, 4],
[3, 4]])
「+ =や* =などの一部の操作は、新しい配列を作成するのではなく、既存の配列を変更する。」
>>> rg = np.random.default_rng(1) # create instance of default random number generator
>>> a = np.ones((2,3), dtype=int)
>>> b = rg.random((2,3))
>>> a *= 3
>>> a
array([[3, 3, 3],
[3, 3, 3]])
>>> b += a
>>> b # 既存のbの値が変わった
array([[3.51182162, 3.9504637 , 3.14415961],
[3.94864945, 3.31183145, 3.42332645]])
>>> a += b # b is not automatically converted to integer type
Traceback (most recent call last):
...
numpy.core._exceptions.UFuncTypeError: Cannot cast ufunc 'add' output from dtype('float64') to dtype('int32') with casting rule 'same_kind'
「異なるタイプの配列を操作する場合、結果の配列のタイプは、より一般的または正確な配列に対応します(アップキャストと呼ばれる動作)。」
>>> a = np.ones(3, dtype=np.int32)
>>> a
array([1, 1, 1])
>>> b = np.linspace(0,np.pi,3)
>>> b
array([0. , 1.57079633, 3.14159265])
>>> b.dtype.name
'float64'
>>> c = a+b
>>> c
array([1. , 2.57079633, 4.14159265])
>>> c.dtype.name
'float64'
>>> c*1j
array([0.+1.j , 0.+2.57079633j, 0.+4.14159265j])
>>> d = np.exp(c*1j)
>>> d
array([ 0.54030231+0.84147098j, -0.84147098+0.54030231j,
-0.54030231-0.84147098j])
>>> d.dtype.name
'complex128'
「配列内のすべての要素の合計の計算など、多くの単項演算は、ndarrayクラスのメソッドとして実装されています。」
>>> rg = np.random.default_rng(1) # create instance of default random number generator
>>> a = np.ones((2,3), dtype=int)
>>> a = rg.random((2,3))
>>> a
array([[0.82770259, 0.40919914, 0.54959369],
[0.02755911, 0.75351311, 0.53814331]])
>>> a.sum() #要素の合計
3.1057109529998157
>>> a.min() #要素の最小値
0.027559113243068367
>>> a.max() #要素の最大値
0.8277025938204418
>>> b = np.arange(12).reshape(3,4)
>>> b
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> b.sum(axis=0) # sum of each column 各列の和
array([12, 15, 18, 21])
>>> b.min(axis=1) # min of each row 各行の最小値
array([0, 4, 8])
>>> b.cumsum(axis=1) # cumulative sum along each row 各行に沿って累積和
array([[ 0, 1, 3, 6],
[ 4, 9, 15, 22],
[ 8, 17, 27, 38]], dtype=int32)
>>> b.cumsum(axis=0) # cumulative sum along each column 各列に沿って累積和
array([[ 0, 1, 2, 3],
[ 4, 6, 8, 10],
[12, 15, 18, 21]], dtype=int32)
Universal Functions
「NumPyは、sin、cos、expなどの使い慣れた数学関数を提供します。 NumPyでは、これらは「ユニバーサル関数」(ufunc)と呼ばれます。 NumPy内では、これらの関数は配列に対して要素ごとに動作し、出力として配列を生成します。」
>>> B = np.arange(3)
>>> B
array([0, 1, 2])
>>> np.exp(B)
array([1. , 2.71828183, 7.3890561 ])
>>> np.sqrt(B)
array([0. , 1. , 1.41421356])
>>> C = np.array([2., -1., 4.])
>>> np.add(B, C)
array([2., 0., 6.])
See also
all, any, apply_along_axis, argmax, argmin, argsort, average, bincount, ceil, clip, conj, corrcoef, cov, cross, cumprod, cumsum, diff, dot, floor, inner, invert, lexsort, max, maximum, mean, median, min, minimum, nonzero, outer, prod, re, round, sort, std, sum, trace, transpose, var, vdot, vectorize, where
Indexing, Slicing and Iterating(インデックス作成、スライス、反復)
「1次元配列は、リストや他のPythonシーケンスと同様に、インデックス付け、スライス、反復が可能です。」
>>> a = np.arange(10)**3
>>> a
array([ 0, 1, 8, 27, 64, 125, 216, 343, 512, 729], dtype=int32)
>>> a[2]
8
>>> a[2:5]
array([ 8, 27, 64], dtype=int32)
>>> a[:6:2] = 1000
>>> a
array([1000, 1, 1000, 27, 1000, 125, 216, 343, 512, 729],
dtype=int32)
>>> a[ : :-1]
array([ 729, 512, 343, 216, 125, 1000, 27, 1000, 1, 1000],
dtype=int32)
>>> for i in a:
... print(i**(1/3.))
...
9.999999999999998
1.0
9.999999999999998
3.0
9.999999999999998
5.0
5.999999999999999
6.999999999999999
7.999999999999999
8.999999999999998
「多次元配列は、軸ごとに1つのインデックスを持つことができます。これらのインデックスは、コンマで区切られたタプルで指定されます。」
>>> def f(x,y):
... return 10*x+y
...
>>> b = np.fromfunction(f,(5,4),dtype=int)
>>> b
array([[ 0, 1, 2, 3],
[10, 11, 12, 13],
[20, 21, 22, 23],
[30, 31, 32, 33],
[40, 41, 42, 43]])
>>> b[2,3] # 2(3行目)の3(4番目) カウント0から
23
>>> b[0:5, 1] # each row in the second column of b
array([ 1, 11, 21, 31, 41])
>>> b[ : ,1] # equivalent to the previous example
array([ 1, 11, 21, 31, 41])
>>> b[1:3, : ] # each column in the second and third row of b
array([[10, 11, 12, 13],
[20, 21, 22, 23]])
>>> b[-1] # the last row. Equivalent to b[-1,:]
array([40, 41, 42, 43])
「括弧内のb [i]内の式は、残りの軸を表すために必要な数の:の後に続くiとして扱われます。
NumPyでは、ドットをb [i、...]として使用してこれを記述することもできます。」
「ドット(...)は、完全なインデックス付けタプルを生成するために必要な数のコロンを表します。たとえば、xが5軸の配列の場合、」
・x[1,2,...] は x[1,2,:,:,:]と同等
・x[...,3] は x[:,:,:,:,3] および
・x[4,...,5,:] は x[4,:,:,5,:]と同等
>>> c = np.array( [[[ 0, 1, 2], # a 3D array (two stacked 2D arrays)
... [ 10, 12, 13]],
... [[100,101,102],
... [110,112,113]]])
>>> c.shape
(2, 2, 3)
>>> c[1,...] # same as c[1,:,:] or c[1]
array([[100, 101, 102],
[110, 112, 113]])
>>> c[...,2] # same as c[:,:,2]
array([[ 2, 13],
[102, 113]])
「多次元配列の反復は、最初の軸に対して行われます。」
※上のbを使っています
>>> for row in b:
... print(row)
...
[0 1 2 3]
[10 11 12 13]
[20 21 22 23]
[30 31 32 33]
[40 41 42 43]
「ただし、配列の各要素に対して操作を実行する場合は、配列のすべての要素の反復子であるflat属性を使用できます。」
>>> for element in b.flat:
... print(element)
...
0
1
2
3
10
11
12
13
20
21
22
23
30
31
32
33
40
41
42
43
See also
Indexing, Indexing (reference), newaxis, ndenumerate, indices
Shape Manipulation
Changing the shape of an array
「配列は、各軸に沿った要素の数によって与えられる形状を持っています:」
>>> a = np.floor(10*rg.random((3,4)))
>>> a
array([[3., 7., 3., 4.],
[1., 4., 2., 2.],
[7., 2., 4., 9.]])
>>> a.shape
(3, 4)
floor
「配列の形状はさまざまなコマンドで変更できます。
次の3つのコマンドはすべて変更された配列を返しますが、元の配列は変更しないことに注意してください。」
>>> a.ravel()
array([3., 7., 3., 4., 1., 4., 2., 2., 7., 2., 4., 9.])
>>> a.reshape(6,2)
array([[3., 7.],
[3., 4.],
[1., 4.],
[2., 2.],
[7., 2.],
[4., 9.]])
>>> a.T
array([[3., 1., 7.],
[7., 4., 2.],
[3., 2., 4.],
[4., 2., 9.]])
>>> a.T.shape
(4, 3)
>>> a.shape
(3, 4)
「ravel()の結果の配列内の要素の順序は通常「Cスタイル」です。
つまり、右端のインデックスが「最も速く変化する」ため、a [0,0]の後の要素はa [0,1]です。 。配列が別の形状に再形成された場合も、配列は「Cスタイル」として扱われます。 NumPyは通常、この順序で格納された配列を作成するため、ravel()は通常、その引数をコピーする必要はありませんが、配列が別の配列のスライスを取得することによって作成された場合、または異常なオプションで作成された場合は、コピーする必要がある場合があります。関数ravel()およびreshape()は、オプションの引数を使用して、左端のインデックスが最も速く変化するFORTRANスタイルの配列を使用するように指示することもできます。」>>> a
array([[3., 7., 3., 4.],
[1., 4., 2., 2.],
[7., 2., 4., 9.]])
>>> a.resize((2,6))
>>> a
array([[3., 7., 3., 4., 1., 4.],
[2., 2., 7., 2., 4., 9.]])
「形状変更操作で次元が-1として指定された場合、他の次元は自動的に計算されます。」
>>> a.reshape(3,-1)
array([[3., 7., 3., 4.],
[1., 4., 2., 2.],
[7., 2., 4., 9.]])
See also
ndarray.shape, reshape, resize, ravel
Stacking together different arrays
「いくつかの配列は、異なる軸に沿って一緒に積み重ねることができます:」
>>> a = np.floor(10*rg.random((2,2)))
>>> a
array([[0., 5.],
[4., 0.]])
>>> b = np.floor(10*rg.random((2,2)))
>>> b
array([[6., 8.],
[5., 2.]])
>>> np.vstack((a,b))
array([[0., 5.],
[4., 0.],
[6., 8.],
[5., 2.]])
>>> np.hstack((a,b))
array([[0., 5., 6., 8.],
[4., 0., 5., 2.]])
「関数column_stackは、1D配列を列として2D配列にスタックします。 2D配列の場合のみ、hstackと同等です。」
>>> from numpy import newaxis
>>> np.column_stack((a,b)) # with 2D arrays
array([[0., 5., 6., 8.],
[4., 0., 5., 2.]])
>>> a = np.array([4.,2.])
>>> b = np.array([3.,8.])
>>> np.column_stack((a,b)) # returns a 2D array
array([[4., 3.],
[2., 8.]])
>>> np.hstack((a,b)) # the result is different
array([4., 2., 3., 8.])
>>> a[:,newaxis] # view `a` as a 2D column vector
array([[4.],
[2.]])
>>> np.column_stack((a[:,newaxis],b[:,newaxis]))
array([[4., 3.],
[2., 8.]])
>>> np.hstack((a[:,newaxis],b[:,newaxis])) # the result is the same
array([[4., 3.],
[2., 8.]])
「一方、row_stack関数は、入力配列のvstackと同等です。実際、row_stackはvstackのエイリアスです。」
>>> np.column_stack is np.hstack
False
>>> np.row_stack is np.vstack
True
「一般に、2次元を超える配列の場合、hstackは2番目の軸に沿ってスタックし、vstackは最初の軸に沿ってスタックし、concatenateは、連結が発生する軸の数を指定するオプションの引数を許可します。」
Note
「複雑なケースでは、r_とc_は、1つの軸に沿って数値を積み重ねて配列を作成するのに役立ちます。範囲リテラル(「:」)を使用できます」
>>> np.r_[1:4,0,4]
array([1, 2, 3, 0, 4])
「配列を引数として使用すると、r_およびc_はデフォルトの動作がvstackおよびhstackと似ていますが、連結する軸の数を指定するオプションの引数を許可します。」
See also
hstack, vstack, column_stack, concatenate, c_, r_
配列をいくつの小さな配列に分割する
「hsplitを使用すると、返される均等に整形された配列の数を指定するか、分割が発生する列を指定することにより、水平軸に沿って配列を分割できます。」
>>> a = np.floor(10*rg.random((2,12)))
>>> a
array([[8., 5., 5., 7., 1., 8., 6., 7., 1., 8., 1., 0.],
[8., 8., 8., 4., 2., 0., 6., 7., 8., 2., 2., 6.]])
>>> np.hsplit(a,3)
[array([[8., 5., 5., 7.],
[8., 8., 8., 4.]]), array([[1., 8., 6., 7.],
[2., 0., 6., 7.]]), array([[1., 8., 1., 0.],
[8., 2., 2., 6.]])]
>>> np.hsplit(a,(3,4))
[array([[8., 5., 5.],
[8., 8., 8.]]), array([[7.],
[4.]]), array([[1., 8., 6., 7., 1., 8., 1., 0.],
[2., 0., 6., 7., 8., 2., 2., 6.]])]
「vsplitは垂直軸に沿って分割し、array_splitは分割する軸に沿って指定できます。」
Copies and Views
「配列を操作するとき、それらのデータは新しい配列にコピーされる場合とコピーされない場合があります。これは、初心者にとってしばしば混乱の元になります。 3つのケースがあります。」
No Copy at All
「単純な割り当てでは、オブジェクトやそのデータのコピーは作成されません。」
>>> a = np.array([[ 0, 1, 2, 3],
... [ 4, 5, 6, 7],
... [ 8, 9, 10, 11]])
>>> b = a # no new object is created
>>> b is a # a and b are two names for the same ndarray object
True
「Pythonは可変オブジェクトを参照として渡すため、関数呼び出しはコピーを作成しません。」
>>> def f(x):
... print(id(x))
...
>>> id(a) # id is a unique identifier of an object
1417178732864
>>> f(a)
1417178732864
View or Shallow Copy
「異なる配列オブジェクトが同じデータを共有できます。 viewメソッドは、同じデータを参照する新しい配列オブジェクトを作成します。」
>>> c = a.view()
>>> c is a
False
>>> c.base is a # c is a view of the data owned by a
True
>>> c.flags.owndata
False
>>> c = c.reshape((2, 6)) # a's shape doesn't change
>>> a.shape
(3, 4)
>>> c[0, 4] = 1234 # a's data changes
>>> a
array([[ 0, 1, 2, 3],
[1234, 5, 6, 7],
[ 8, 9, 10, 11]])
「配列をスライスすると、そのビューが返されます。」
>>> s = a[ : , 1:3] # spaces added for clarity; could also be written "s = a[:, 1:3]"
>>> s
array([[ 1, 2],
[ 5, 6],
[ 9, 10]])
>>> s[:] = 10 # s[:] is a view of s. Note the difference between s = 10 and s[:] = 10
>>> s
array([[10, 10],
[10, 10],
[10, 10]])
>>> a
array([[ 0, 10, 10, 3],
[1234, 10, 10, 7],
[ 8, 10, 10, 11]])
Deep Copy
「copyメソッドは、配列とそのデータの完全なコピーを作成します。」
>>> d = a.copy() # a new array object with new data is created
>>> d
array([[ 0, 10, 10, 3],
[1234, 10, 10, 7],
[ 8, 10, 10, 11]])
>>> d is a # d doesn't share anything with a
False
>>> d[0,0] = 9999
>>> a
array([[ 0, 10, 10, 3],
[1234, 10, 10, 7],
[ 8, 10, 10, 11]])
>>> d
array([[9999, 10, 10, 3],
[1234, 10, 10, 7],
[ 8, 10, 10, 11]])
「元の配列が不要になった場合は、スライス後にcopyを呼び出す必要があります。
たとえば、aが巨大な中間結果であり、最終結果bに含まれるのはaのごく一部であるとすると、スライスを使用してbを構築するときに、深いコピーを作成する必要があります。」
>>> a = np.arange(int(1e8))
>>> b = a[:100].copy()
>>> del a
>>> a
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
NameError: name 'a' is not defined
>>> b
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50,
51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67,
68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84,
85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99])
「代わりにb = a [:100]が使用されている場合、aはbによって参照され、del aが実行されてもメモリに保持されます。」
⇒挙動の差が無かったのでこの部分不明です
>>> a = np.arange(int(1e8))
>>> b = a[:100]
>>> b
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50,
51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67,
68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84,
85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99])
>>> del a
>>> b
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50,
51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67,
68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84,
85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99])
>>> a
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
NameError: name 'a' is not defined
Functions and Methods Overview
「以下は、いくつかの便利なNumPy関数とメソッド名の一覧です。完全なリストについては、ルーチンを参照してください。」
Array Creation
arange, array, copy, empty, empty_like, eye, fromfile, fromfunction, identity, linspace, logspace, mgrid, ogrid, ones, ones_like, r_, zeros, zeros_like
Conversions
ndarray.astype, atleast_1d, atleast_2d, atleast_3d, mat
Manipulations
array_split, column_stack, concatenate, diagonal, dsplit, dstack, hsplit, hstack, ndarray.item, newaxis, ravel, repeat, reshape, resize, squeeze, swapaxes, take, transpose, vsplit, vstack
Questions
all, any, nonzero, where
Ordering
argmax, argmin, argsort, max, min, ptp, searchsorted, sort
Operations
choose, compress, cumprod, cumsum, inner, ndarray.fill, imag, prod, put, putmask, real, sum
Basic Statistics
cov, mean, std, var
Basic Linear Algebra
cross, dot, outer, linalg.svd, vdot
Less Basic
Broadcasting rules
...省略
Advanced indexing and index tricks
「NumPyは、通常のPythonシーケンスよりも多くのインデックス機能を提供します。前に見たように、整数とスライスによるインデックス付けに加えて、配列は整数の配列とブール値の配列によってインデックス付けできます。」
Indexing with Arrays of Indices
>>> a = np.arange(12)**2 # the first 12 square numbers
>>> i = np.array([1, 1, 3, 8, 5]) # an array of indices
>>> a[i] # the elements of a at the positions i
array([ 1, 1, 9, 64, 25], dtype=int32)
>>> j = np.array([[3, 4], [9, 7]]) # a bidimensional array of indices
>>> a[j] # the same shape as j
array([[ 9, 16],
[81, 49]], dtype=int32)
「インデックス付き配列aが多次元の場合、インデックスの単一の配列はaの最初の次元を参照します。次の例は、パレットを使用してラベルの画像をカラー画像に変換することにより、この動作を示しています。」
>>> palette = np.array([[0, 0, 0], # black
... [255, 0, 0], # red
... [0, 255, 0], # green
... [0, 0, 255], # blue
... [255, 255, 255]]) # white
>>> image = np.array([[0, 1, 2, 0], # each value corresponds to a color in the palette
... [0, 3, 4, 0]])
>>> palette[image] # the (2, 4, 3) color image
array([[[ 0, 0, 0],
[255, 0, 0],
[ 0, 255, 0],
[ 0, 0, 0]],
[[ 0, 0, 0],
[ 0, 0, 255],
[255, 255, 255],
[ 0, 0, 0]]])
「また、複数の次元のインデックスを指定することもできます。各次元のインデックスの配列は、同じ形状でなければなりません。」
>>> a = np.arange(12).reshape(3,4)
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> i = np.array([[0, 1], # indices for the first dim of a
... [1, 2]])
>>> j = np.array([[2, 1], # indices for the second dim
... [3, 3]])
>>> a[i, j] # i and j must have equal shape
array([[ 2, 5],
[ 7, 11]])
>>> a[i, 2]
array([[ 2, 6],
[ 6, 10]])
>>> a[:, j] # i.e., a[ : , j]
array([[[ 2, 1],
[ 3, 3]],
[[ 6, 5],
[ 7, 7]],
[[10, 9],
[11, 11]]])
「
Pythonでは、arr [i、j]はarr [(i、j)]とまったく同じです。つまり、iとjをタプルに入れ、それを使用してインデックスを作成できます。」
>>> t = (i, j)
>>> a[t]
array([[ 2, 5],
[ 7, 11]])
>>> s = np.array([i, j])
>>> s
array([[[0, 1],
[1, 2]],
[[2, 1],
[3, 3]]])
>>> a[s]
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
IndexError: index 3 is out of bounds for axis 0 with size 3
>>> a[tuple(s)]
array([[ 2, 5],
[ 7, 11]])
>>> tuple(s)
(array([[0, 1],
[1, 2]]), array([[2, 1],
[3, 3]]))
「配列を使用したインデックス付けのもう1つの一般的な用途は、時間依存系列の最大値の検索です。」
>>> time = np.linspace(20, 145, 5) # time scale
>>> data = np.sin(np.arange(20)).reshape(5,4) # 4 time-dependent series
>>> time
array([ 20. , 51.25, 82.5 , 113.75, 145. ])
>>> data
array([[ 0. , 0.84147098, 0.90929743, 0.14112001],
[-0.7568025 , -0.95892427, -0.2794155 , 0.6569866 ],
[ 0.98935825, 0.41211849, -0.54402111, -0.99999021],
[-0.53657292, 0.42016704, 0.99060736, 0.65028784],
[-0.28790332, -0.96139749, -0.75098725, 0.14987721]])
>>> ind = data.argmax(axis=0)
>>> ind
array([2, 0, 3, 1], dtype=int64)
>>> time_max = time[ind]
>>> data_max = data[ind, range(data.shape[1])]
>>> time_max
array([ 82.5 , 20. , 113.75, 51.25])
>>> data_max
array([0.98935825, 0.84147098, 0.99060736, 0.6569866 ])
>>> np.all(data_max == data.max(axis=0))
True
「配列のインデックスをターゲットとして使用して、以下を割り当てることもできます。」
>>> a = np.arange(5)
>>> a
array([0, 1, 2, 3, 4])
>>> a[[1,3,4]] = 0
>>> a
array([0, 0, 2, 0, 0])
「ただし、インデックスのリストに繰り返しが含まれている場合、割り当ては数回行われ、最後の値が残ります。」
>>> a = np.arange(5)
>>> a
array([0, 1, 2, 3, 4])
>>> a[[0,0,2]]=[1,2,3]
>>> a
array([2, 1, 3, 3, 4])
「これは十分に妥当ですが、Pythonの+ =構文を使用する場合は、期待どおりに動作しない可能性があるので注意してください。」
>>> a = np.arange(5)
>>> a[[0,0,2]]+=1
>>> a
array([1, 1, 3, 3, 4])
「インデックスのリストで0が2回発生しても、0番目の要素は1回だけインクリメントされます。これは、Pythonでは「a + = 1」が「a = a + 1」と同等である必要があるためです。」
Indexing with Boolean Arrays
「(整数)インデックスの配列で配列にインデックスを付けるとき、選択するインデックスのリストを提供します。ブールインデックスでは、アプローチが異なります。配列内の必要な項目と不要な項目を明示的に選択します。」
「ブール型のインデックス付けについて考えることができる最も自然な方法は、元の配列と同じ形状を持つブール配列を使用することです。」
>>> a = np.arange(12).reshape(3,4)
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> b = a > 4
>>> b
array([[False, False, False, False],
[False, True, True, True],
[ True, True, True, True]])
>>> a[b]
array([ 5, 6, 7, 8, 9, 10, 11])
「このプロパティは、割り当てに非常に役立ちます。」
>>> a[b] = 0
>>> a
array([[0, 1, 2, 3],
[4, 0, 0, 0],
[0, 0, 0, 0]])
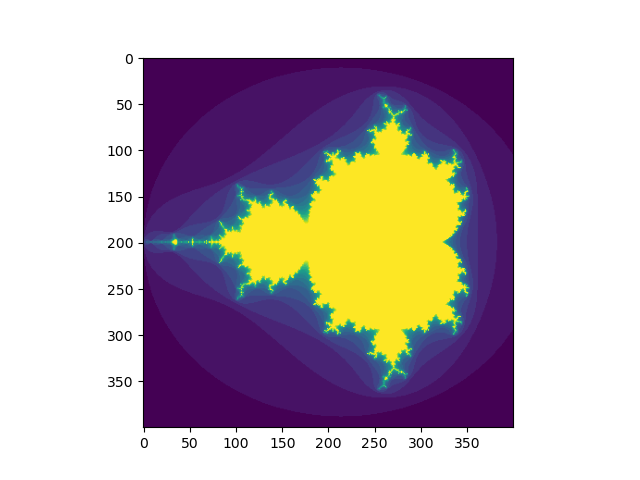
「次の例を見て、ブールインデックスを使用してマンデルブロ集合のイメージを生成する方法を確認できます。」
import numpy as np
import matplotlib.pyplot as plt
def mandelbrot( h,w, maxit=20 ):
"""Returns an image of the Mandelbrot fractal of size (h,w)."""
y,x = np.ogrid[ -1.4:1.4:h*1j, -2:0.8:w*1j ]
c = x+y*1j
z = c
divtime = maxit + np.zeros(z.shape, dtype=int)
for i in range(maxit):
z = z**2 + c
diverge = z*np.conj(z) > 2**2 # who is diverging
div_now = diverge & (divtime==maxit) # who is diverging now
divtime[div_now] = i # note when
z[diverge] = 2 # avoid diverging too much
return divtime
plt.imshow(mandelbrot(400,400))
plt.show()
「ブール値を使用したインデックス作成の2番目の方法は、整数のインデックス作成により似ています。配列の各次元について、必要なスライスを選択する1Dブール配列を提供します。」
>>> a = np.arange(12).reshape(3,4)
>>> b1 = np.array([False,True,True])
>>> b2 = np.array([True,False,True,False])
>>> a[b1,:]
array([[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> a[b1]
array([[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> a[:,b2]
array([[ 0, 2],
[ 4, 6],
[ 8, 10]])
>>> a[b1,b2]
array([ 4, 10])
「1Dブール配列の長さは、スライスする次元(または軸)の長さと一致する必要があることに注意してください。前の例では、b1の長さは3(aの行数)であり、b2(長さ4の)はaの2番目の軸(列)のインデックス付けに適しています。」
The ix_() function
「ix_関数は、各n-upletの結果を取得するために、異なるベクトルを組み合わせるために使用できます。たとえば、ベクトルa、b、cから取得したすべてのトリプレットのすべてのa + b * cを計算する場合は、次のようになります。」
>>> a = np.array([2,3,4,5])
>>> b = np.array([8,5,4])
>>> c = np.array([5,4,6,8,3])
>>> ax,bx,cx = np.ix_(a,b,c)
>>> ax
array([[[2]],
[[3]],
[[4]],
[[5]]])
>>> bx
array([[[8],
[5],
[4]]])
>>> cx
array([[[5, 4, 6, 8, 3]]])
>>> ax.shape, bx.shape, cx.shape
((4, 1, 1), (1, 3, 1), (1, 1, 5))
>>> result = ax+bx*cx
>>> result
array([[[42, 34, 50, 66, 26],
[27, 22, 32, 42, 17],
[22, 18, 26, 34, 14]],
[[43, 35, 51, 67, 27],
[28, 23, 33, 43, 18],
[23, 19, 27, 35, 15]],
[[44, 36, 52, 68, 28],
[29, 24, 34, 44, 19],
[24, 20, 28, 36, 16]],
[[45, 37, 53, 69, 29],
[30, 25, 35, 45, 20],
[25, 21, 29, 37, 17]]])
>>> result[3,2,4]
17
>>> a[3]+b[2]*c[4]
17
「次のように削減を実装することもできます。」
>>> def ufunc_reduce(ufct, *vectors):
... vs = np.ix_(*vectors)
... r = ufct.identity
... for v in vs:
... r = ufct(r,v)
... return r
...
>>> ufunc_reduce(np.add,a,b,c)
array([[[15, 14, 16, 18, 13],
[12, 11, 13, 15, 10],
[11, 10, 12, 14, 9]],
[[16, 15, 17, 19, 14],
[13, 12, 14, 16, 11],
[12, 11, 13, 15, 10]],
[[17, 16, 18, 20, 15],
[14, 13, 15, 17, 12],
[13, 12, 14, 16, 11]],
[[18, 17, 19, 21, 16],
[15, 14, 16, 18, 13],
[14, 13, 15, 17, 12]]])
「通常のufunc.reduceと比較したこのバージョンのreduceの利点は、出力のサイズにベクトルの数を掛けた引数配列の作成を回避するために、ブロードキャストルールを利用することです。」
Indexing with strings
See Structured arrays.
Linear Algebra
See linalg.py in numpy folder for more.
>>> a = np.array([[1.0, 2.0], [3.0, 4.0]])
>>> print(a)
[[1. 2.]
[3. 4.]]
>>> a.transpose() #転置行列
array([[1., 3.],
[2., 4.]])
>>> np.linalg.inv(a) #逆行列
array([[-2. , 1. ],
[ 1.5, -0.5]])
>>> u = np.eye(2) #単位行列 # unit 2x2 matrix; "eye" represents "I"
>>> u
array([[1., 0.],
[0., 1.]])
>>> j = np.array([[0.0, -1.0], [1.0, 0.0]])
>>> j @ j #行列積
array([[-1., 0.],
[ 0., -1.]])
>>> np.trace(u) #対角和
2.0
>>> y = np.array([[5.], [7.]])
>>> np.linalg.solve(a, y) #固有値問題の解
array([[-3.],
[ 4.]])
>>> np.linalg.eig(j) #固有値
(array([0.+1.j, 0.-1.j]), array([[0.70710678+0.j , 0.70710678-0.j ],
[0. -0.70710678j, 0. +0.70710678j]]))
Tricks and Tips
“Automatic” Reshaping
「配列の次元を変更するには、自動的に推定されるサイズの1つを省略できます。」
>>> a = np.arange(30)
>>> b = a.reshape((2, -1, 3)) #-1と省略できる
>>> b.shape
(2, 5, 3)
>>> b
array([[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11],
[12, 13, 14]],
[[15, 16, 17],
[18, 19, 20],
[21, 22, 23],
[24, 25, 26],
[27, 28, 29]]])
Vector Stacking
「等しいサイズの行ベクトルのリストから2D配列を構築するにはどうすればよいですか?これは、MATLABでは非常に簡単です。xとyが同じ長さの2つのベクトルである場合、m = [x; y]を実行するだけで済みます。 NumPyでは、これは、スタッキングが行われるディメンションに応じて、関数column_stack、dstack、hstackおよびvstackを介して機能します。例えば:」
>>> x = np.arange(0,10,2)
>>> y = np.arange(5)
>>> m = np.vstack([x,y])
>>> m
array([[0, 2, 4, 6, 8],
[0, 1, 2, 3, 4]])
>>> xy = np.hstack([x,y])
>>> xy
array([0, 2, 4, 6, 8, 0, 1, 2, 3, 4])
「3次元以上でのこれらの関数の背後にあるロジックは奇妙な場合があります。」
See also
NumPy for Matlab users
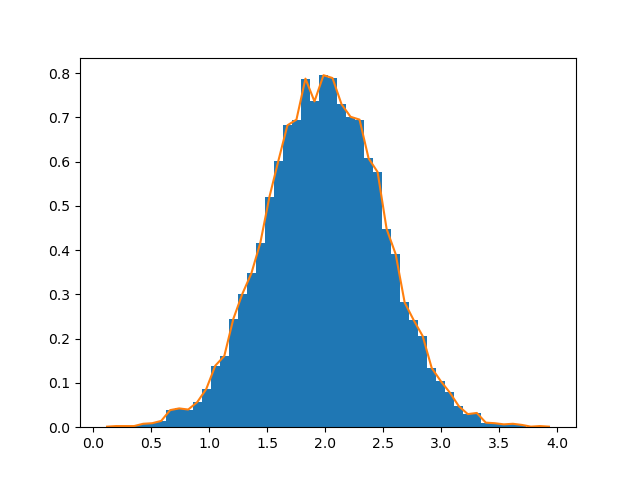
Histograms
rg = np.random.default_rng(1)
import matplotlib.pyplot as plt
# Build a vector of 10000 normal deviates with variance 0.5^2 and mean 2
mu, sigma = 2, 0.5
v = rg.normal(mu,sigma,10000)
# Plot a normalized histogram with 50 bins
plt.hist(v, bins=50, density=1) # matplotlib version (plot)
# Compute the histogram with numpy and then plot it
(n, bins) = np.histogram(v, bins=50, density=True) # NumPy version (no plot)
plt.plot(.5*(bins[1:]+bins[:-1]), n)
plt.show()
Further reading
・The Python tutorial
・NumPy Reference
・SciPy Tutorial
・SciPy Lecture Notes
・A matlab, R, IDL, NumPy/SciPy dictionary
まとめ
・Numpy Quickstart tutorialを写経した
・次はScipy tutorialかな