第八夜は、価値ネットワークの解説とtrain_value.pyのコード解説、そして実際の学習について記述します。
###説明したいこと
（１）価値ネットワークとは
（２）train_value.pyのコード解説
（３）価値ネットワークの学習について
###（１）価値ネットワークとは
「価値ネットワークとは、局面を入力として、その局面から対局した場合勝つか負けるかを予測します。これは、２値分類問題です」
「２値分類問題では、出力層のユニットは１つになります。2つの分類に0と1を割り当て、0か1を教師の値として学習します。推論では、１になる確率を出力します。」
「これは評価関数に近いものです。評価関数は、歩1枚の価値を１００点として局面の価値を出力します。評価値は勝率とは異なる値ですが、勝率に変換することが可能です。評価値はロジスティック関数を通すことで勝率に変換できます。」
※上記文章は本書の引用です
ちなみに方策ネットワークは
「局面を入力として指し手を予測するニューラルネットワーク」でした。
一方、今回の価値ネットワークを使った「１手」探索は、以下のような考え方で実施します。
「局面の合法手すべてについて1手指してみて、その1手後の局面の価値を予測します。そして、局面の価値が最も高くなる手を選択します。ここで、１手後の局面の価値は、相手番の価値であることに注意が必要になります。相手番での価値が最も低い局面が、自分の手番で最も価値の高い手になります。相手番の価値を自分の手番の価値にするのには、価値ネットワークの出力の符号を反転します。価値ネットワークの出力は、シグモイド関数に入力する前の値となっているため、原点０で対称な値となっています。」
実はこれら二つのニューラルネットワークを利用するとAlphaZeroのような高度なディープラーニング利用の将棋AIを確立できるのですが、これはモンテカルロ木探索を利用することにより最大化されることを後でみることにします。
※この説明は本書では「理論編 第４章AlphaGoの手法」で説明されています
ということで、ここでは価値ネットワークを使った「１手」探索のために価値ネットワークの学習を説明したいと思う。
###（２）train_value.pyのコード解説
まず価値ネットワークは以前と同じように図で記載すると以下のように書けます。
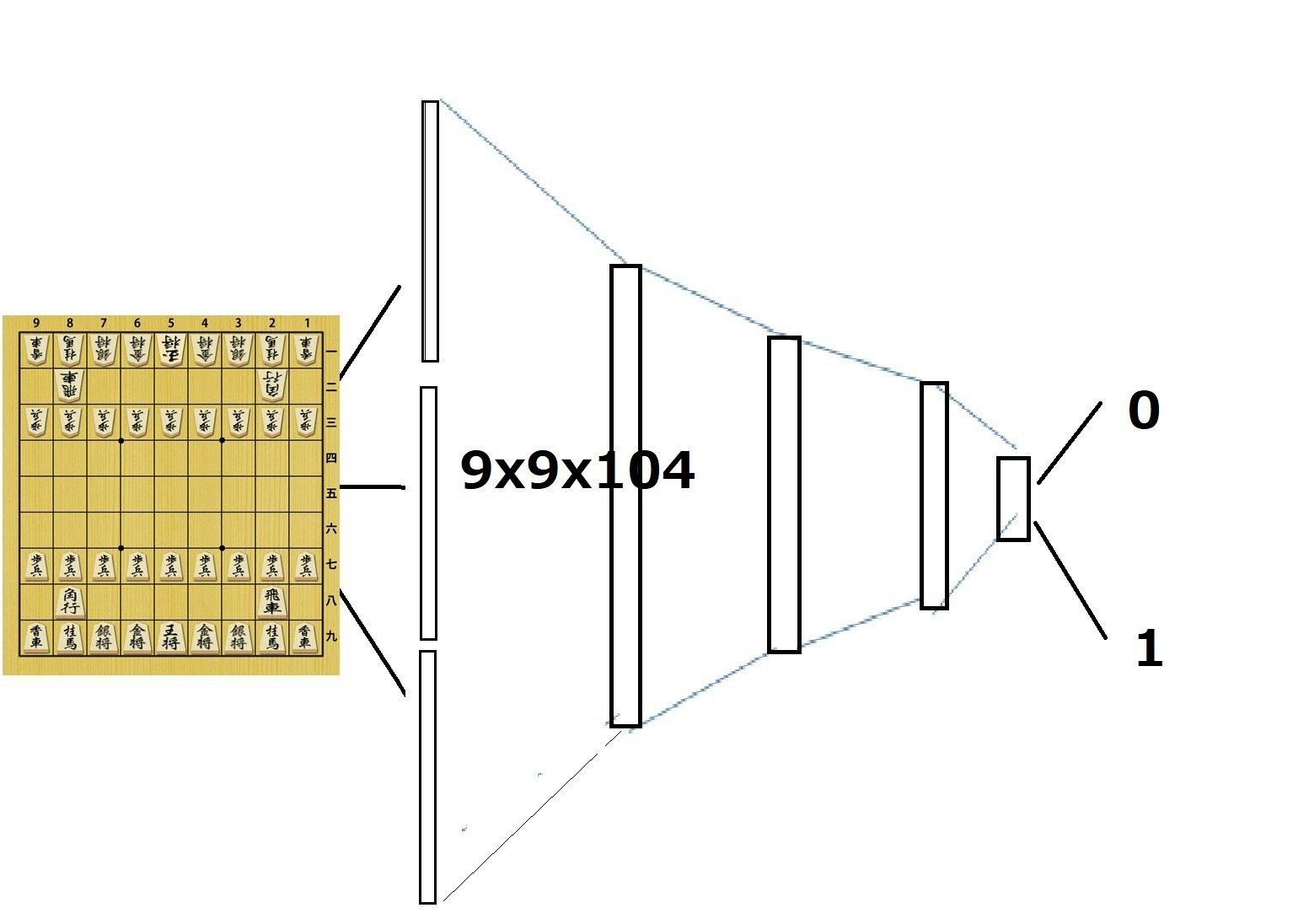
したがって、価値ネットワークは方策ネットワークとほぼ同じ形状で以下のとおりです。
value.py
from chainer import Chain
import chainer.functions as F
import chainer.links as L
from pydlshogi.common import *
ch = 192
fcl = 256
class ValueNetwork(Chain):
def __init__(self):
super(ValueNetwork, self).__init__()
with self.init_scope():
self.l1=L.Convolution2D(in_channels = 104, out_channels = ch, ksize = 3, pad = 1)
self.l2=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
self.l3=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
self.l4=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
self.l5=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
self.l6=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
self.l7=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
self.l8=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
self.l9=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
self.l10=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
self.l11=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
self.l12=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
self.l13_v=L.Convolution2D(in_channels = ch, out_channels = MOVE_DIRECTION_LABEL_NUM, ksize = 1)
self.l14_v=L.Linear(9*9*MOVE_DIRECTION_LABEL_NUM, fcl)
self.l15_v=L.Linear(fcl, 1)
def __call__(self, x):
h1 = F.relu(self.l1(x))
h2 = F.relu(self.l2(h1))
h3 = F.relu(self.l3(h2))
h4 = F.relu(self.l4(h3))
h5 = F.relu(self.l5(h4))
h6 = F.relu(self.l6(h5))
h7 = F.relu(self.l7(h6))
h8 = F.relu(self.l8(h7))
h9 = F.relu(self.l9(h8))
h10 = F.relu(self.l10(h9))
h11 = F.relu(self.l11(h10))
h12 = F.relu(self.l12(h11))
h13_v = F.relu(self.l13_v(h12))
h14_v = F.relu(self.l14_v(h13_v))
return self.l15_v(h14_v)
方策ネットワークと異なるのは、最後の出力層の部分です。
そのために、_vがついている層で明示的に示されています。
self.l13_v=L.Convolution2D(in_channels = ch, out_channels = MOVE_DIRECTION_LABEL_NUM, ksize = 1)
self.l14_v=L.Linear(9*9*MOVE_DIRECTION_LABEL_NUM, fcl)
self.l15_v=L.Linear(fcl, 1)
の３つの層です。
第１３行目でバイアスありのフィルターサイズ１×1の畳み込み層になっています。
第１４行目の全結合層の入力ノード数は、１３層の出力チャンネル数に画像サイズの9×9をかけた値になっています。全結合層のノード数は定数fc1で定義され256としています。
15層目の全結合層は、出力ノード数を１としています。
そして、train_value.pyもほとんど同じようなプログラムです。
違いは以下のとおりです。
Network model名変更；ValueNetwork
modelをmodel_value, state_value
・2値分類問題の場合
loss関数
loss=F.sigmoid_cross_entropy(y)
一致率の計算
F.binary_accuracy(y,t).data
一番大きい変更は
# mini batch
def mini_batch(positions, i, batchsize):
mini_batch_data = []
mini_batch_win = []
for b in range(batchsize):
features, move, win = make_features(positions[i + b])
mini_batch_data.append(features)
mini_batch_win.append(win)
return (Variable(cuda.to_gpu(np.array(mini_batch_data, dtype=np.float32))),
Variable(cuda.to_gpu(np.array(mini_batch_win, dtype=np.int32).reshape((-1, 1)))))
def mini_batch_for_test(positions, batchsize):
mini_batch_data = []
mini_batch_win = []
for b in range(batchsize):
features, move, win = make_features(random.choice(positions))
mini_batch_data.append(features)
mini_batch_win.append(win)
return (Variable(cuda.to_gpu(np.array(mini_batch_data, dtype=np.float32))),
Variable(cuda.to_gpu(np.array(mini_batch_win, dtype=np.int32).reshape((-1, 1)))))
のmini_batch_win.append(win)と勝敗を学習データ、テストデータに読み込むところです。
###（３）価値ネットワークの学習について
いよいよ学習してみます。
>python train_value.py kifulist3000_train.txt kifulist3000_test.txt --eval_interval 100
2018/08/26 22:37:09 INFO read kifu start
2018/08/26 22:37:29 INFO load train pickle
2018/08/26 22:37:31 INFO load test pickle
2018/08/26 22:37:31 INFO read kifu end
2018/08/26 22:37:31 INFO train position num = 1892246
2018/08/26 22:37:31 INFO test position num = 208704
2018/08/26 22:37:31 INFO start training
2018/08/26 22:37:41 INFO epoch = 1, iteration = 100, loss = 0.6931878, accuracy = 0.5
2018/08/26 22:37:44 INFO epoch = 1, iteration = 200, loss = 0.69317496, accuracy = 0.5214844
2018/08/26 22:37:47 INFO epoch = 1, iteration = 300, loss = 0.69310546, accuracy = 0.48632812
2018/08/26 22:37:50 INFO epoch = 1, iteration = 400, loss = 0.6931807, accuracy = 0.53125
2018/08/26 22:37:53 INFO epoch = 1, iteration = 500, loss = 0.6931599, accuracy = 0.5566406
2018/08/26 22:37:56 INFO epoch = 1, iteration = 600, loss = 0.69313407, accuracy = 0.51171875
2018/08/26 22:37:59 INFO epoch = 1, iteration = 700, loss = 0.6930141, accuracy = 0.4921875
2018/08/26 22:38:03 INFO epoch = 1, iteration = 800, loss = 0.6931833, accuracy = 0.45117188
2018/08/26 22:38:06 INFO epoch = 1, iteration = 900, loss = 0.69310683, accuracy = 0.52734375
2018/08/26 22:38:09 INFO epoch = 1, iteration = 1000, loss = 0.69309497, accuracy = 0.5800781
．．．
2018/08/26 23:07:20 INFO epoch = 1, iteration = 58900, loss = 0.6461111, accuracy = 0.59765625
2018/08/26 23:07:23 INFO epoch = 1, iteration = 59000, loss = 0.64717156, accuracy = 0.5917969
2018/08/26 23:07:26 INFO epoch = 1, iteration = 59100, loss = 0.6498045, accuracy = 0.62890625
2018/08/26 23:07:27 INFO validate test data
2018/08/26 23:09:20 INFO epoch = 1, iteration = 59132, train loss avr = 0.6500112, test accuracy = 0.5983409
．．．
2018/08/27 00:36:48 INFO epoch = 4, iteration = 235000, loss = 0.5688383, accuracy = 0.6816406
2018/08/27 00:37:16 INFO epoch = 4, iteration = 236000, loss = 0.57262594, accuracy = 0.6855469
2018/08/27 00:37:30 INFO validate test data
2018/08/27 00:39:20 INFO epoch = 4, iteration = 236528, train loss avr = 0.582965, test accuracy = 0.65962374
．．．
2018/08/27 08:11:58 INFO epoch = 6, iteration = 350000, loss = 0.5175312, accuracy = 0.671875
2018/08/27 08:12:25 INFO epoch = 6, iteration = 351000, loss = 0.5179844, accuracy = 0.67578125
2018/08/27 08:12:53 INFO epoch = 6, iteration = 352000, loss = 0.51888376, accuracy = 0.65234375
2018/08/27 08:13:20 INFO epoch = 6, iteration = 353000, loss = 0.5155886, accuracy = 0.640625
2018/08/27 08:13:48 INFO epoch = 6, iteration = 354000, loss = 0.5247961, accuracy = 0.69921875
2018/08/27 08:14:09 INFO validate test data
2018/08/27 08:15:59 INFO epoch = 6, iteration = 354792, train loss avr = 0.5299229, test accuracy = 0.6576445
．．．
2018/08/27 08:43:18 INFO epoch = 7, iteration = 411000, loss = 0.47353968, accuracy = 0.65625
2018/08/27 08:43:46 INFO epoch = 7, iteration = 412000, loss = 0.4747911, accuracy = 0.66796875
2018/08/27 08:44:13 INFO epoch = 7, iteration = 413000, loss = 0.4722041, accuracy = 0.6582031
2018/08/27 08:44:38 INFO validate test data
2018/08/27 08:46:28 INFO epoch = 7, iteration = 413924, train loss avr = 0.49081746, test accuracy = 0.6562883
．．．
2018/08/27 10:37:37 INFO epoch = 11, iteration = 646000, loss = 0.2781549, accuracy = 0.6621094
2018/08/27 10:38:04 INFO epoch = 11, iteration = 647000, loss = 0.285341, accuracy = 0.6503906
2018/08/27 10:38:32 INFO epoch = 11, iteration = 648000, loss = 0.2768081, accuracy = 0.6328125
2018/08/27 10:38:59 INFO epoch = 11, iteration = 649000, loss = 0.27980852, accuracy = 0.6171875
2018/08/27 10:39:26 INFO epoch = 11, iteration = 650000, loss = 0.28065822, accuracy = 0.625
2018/08/27 10:39:38 INFO validate test data
2018/08/27 10:41:28 INFO epoch = 11, iteration = 650452, train loss avr = 0.28731215, test accuracy = 0.6359119
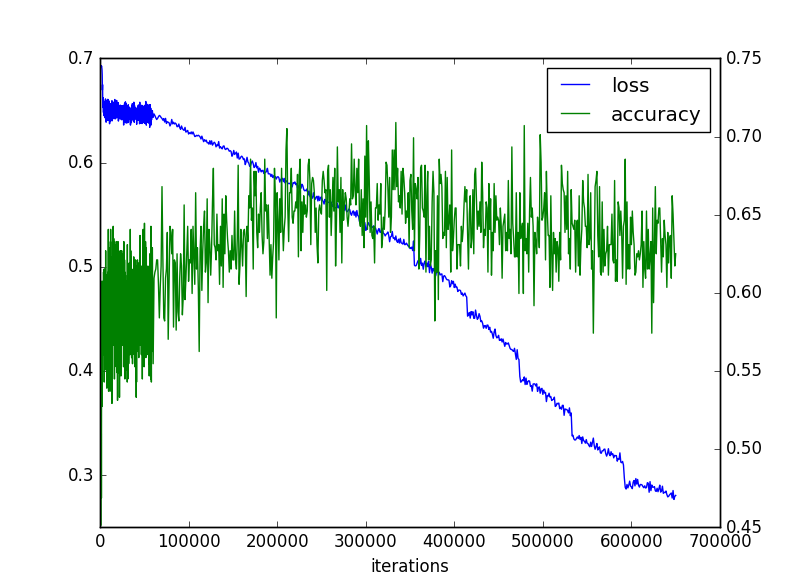
グラフ見ると、一致率は飽和して減少しているが、lossがまだまだ減少していて、継続すべきなのかもしれない。
###まとめ
・価値ネットワークの方策ネットワークとの類似性を説明した
・価値ネットワークの学習のためのコードを説明した
・方策ネットワークと同じデータで学習してみた
・価値ネットワークによる「次の１手」プログラムで対戦したい