昨夜の総合問題のLorenz曲線とGini係数は、調べてみると奥が深そうということで、調べたことまとめておこうと思う。
やったこと
・Lorenz曲線
・Gini係数
・Scipyで数値積分
・導出
・Lorenz曲線
Lorenz曲線とは、
「例えば収入分布を調べる場合、収入をカテゴライズする。カテゴライズされた収入を小さい順に序列化する。そのカテゴリーに属する人数を並列する。それぞれの累積値を計算する。それぞれの累積最大値を1に規格化する。そして、縦軸に規格化された収入累積値、横軸に序列化した順序の規格化数値を描いたとき現れる曲線を云う」
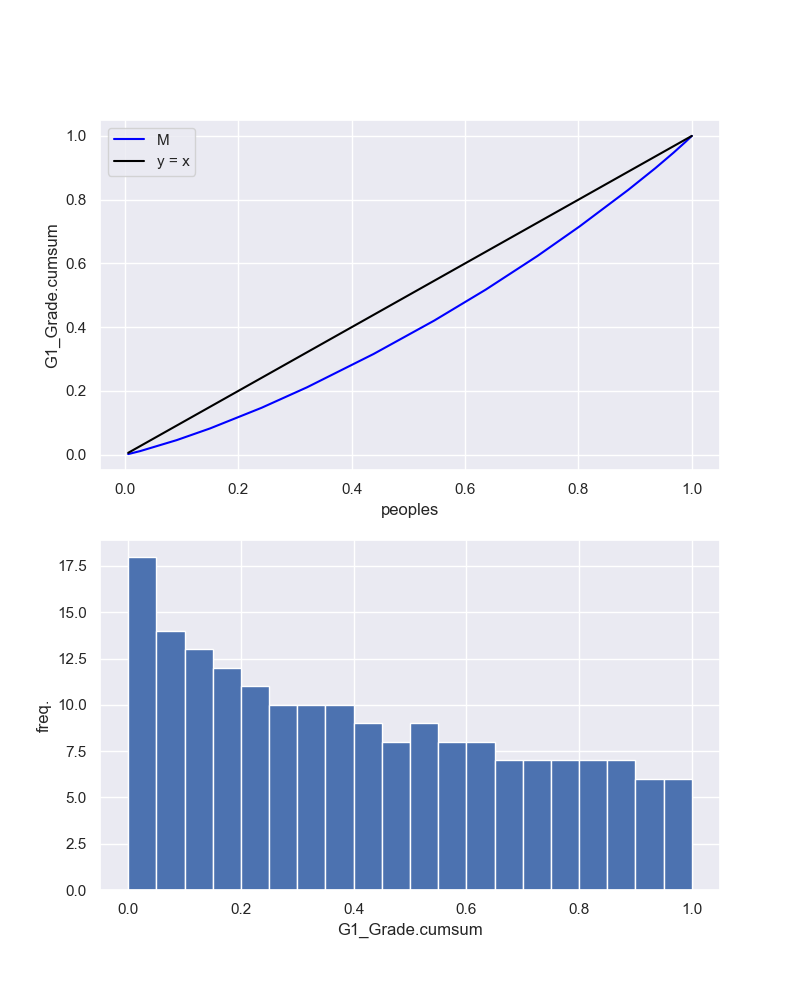
今回は、昨夜の学生の得点分布でLorenz曲線を描く。ここでは、人数が少ないので、カテゴライズせずに序列化・累計のみ実施する。
昨夜のデータから、G1の得点分布は以下のとおり描ける。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# データ取り込み
student_data_math = pd.read_csv('./chap3/student-mat.csv', sep =';')
# 'M'のデータを取得
df0 = student_data_math[student_data_math['sex'].isin(['M'])]
# 'G1'で昇順に序列化
df = df0.sort_values(by=['G1'])
# 'Ct'という数値列を追加
df['Ct']=np.arange(1,len(df)+1)
# xに数値列を代入
x = df['Ct']
# yにG1データの累積値を代入
y = df['G1'].cumsum()
# グラフ描画
fig, (ax1,ax2) = plt.subplots(2, 1, figsize=(8,2*5))
# x,yの最大値で規格化して青線で描画
ax1.plot(x/max(x),y/max(y),'blue', label='M')
# 一様な分布な場合として、y=xのグラフ描画
ax1.plot(x/max(x),x/max(x),'black', label = 'y = x')
# ax2に頻度分布を描画(Gradeが20段階なのでbinz=20)
ax2.hist(y/max(y), bins = 20, range =(0,1),label ='M')
ax1.set_xlabel('peoples')
ax1.set_ylabel('G1_Grade.cumsum')
ax2.set_ylabel('freq.')
ax2.set_xlabel('G1_Grade.cumsum')
ax1.legend()
ax1.grid(True)
plt.show()
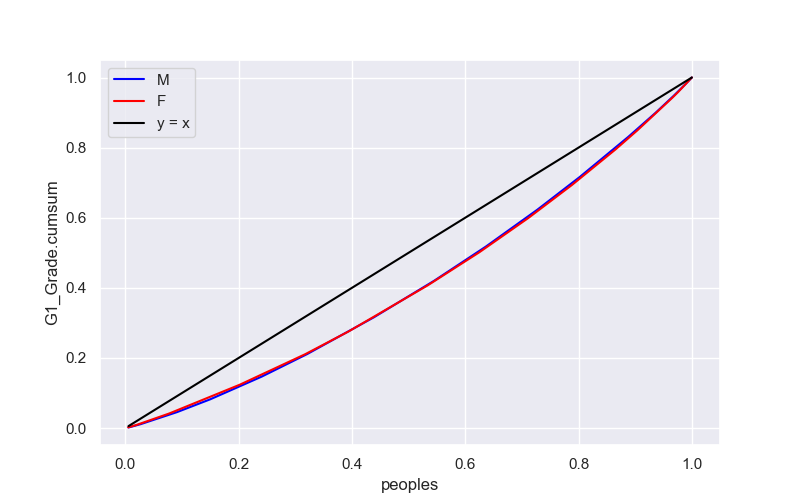
そして、重ねてみると、以下のようになりました。
つまり、男女差はほとんど無いということが分かります。
・Gini係数
参考によれば、Gini係数は上図のy=xのグラフとLorenz曲線とで囲まれた面積の2倍と定義される。
【参考】
・Gini coefficient@wikipedia
以下、参考から引用させていただきます。
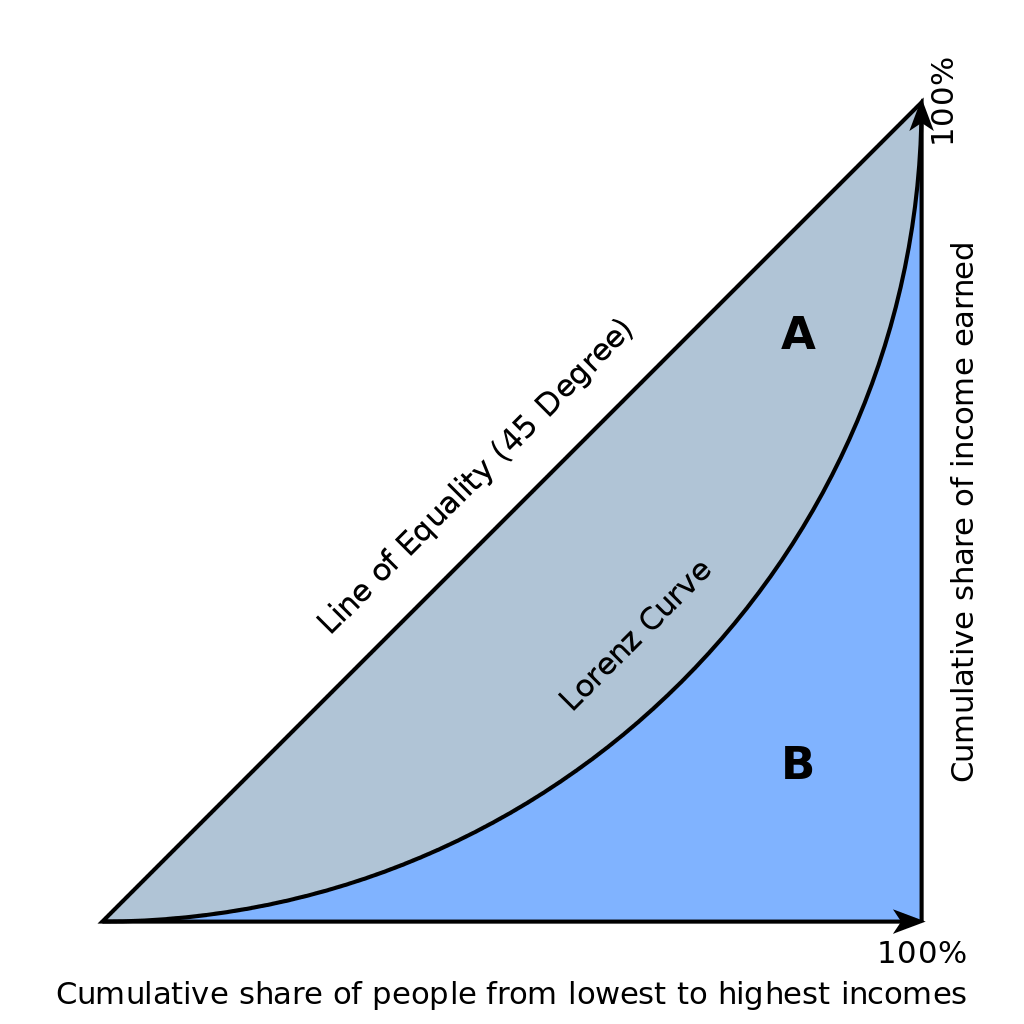
「G = A/(A + B). It is also equal to 2A and to 1 − 2B due to the fact that A + B = 0.5 (since the axes scale from 0 to 1).」
・Scipyで求積
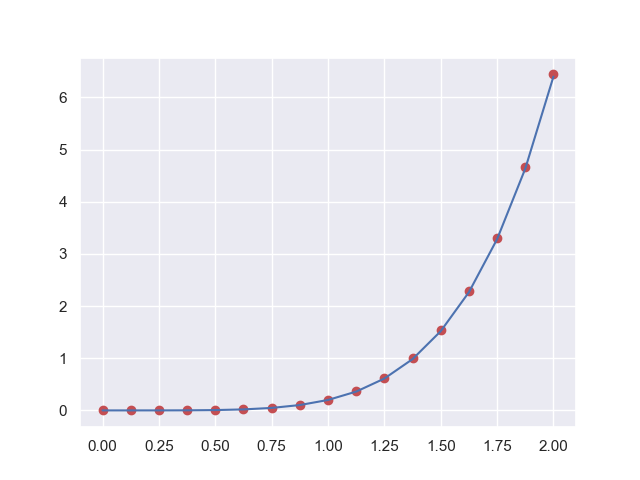
例題 integrate.cumtrapzの使い方
from scipy import integrate
x = np.linspace(0, 2, num=2**4+1)
y = x**4
y_int = integrate.cumtrapz(y, x, initial=0)
plt.plot(x, y_int, 'ro', x, y[0] + 0.2 * x**5, 'b-')
plt.show()
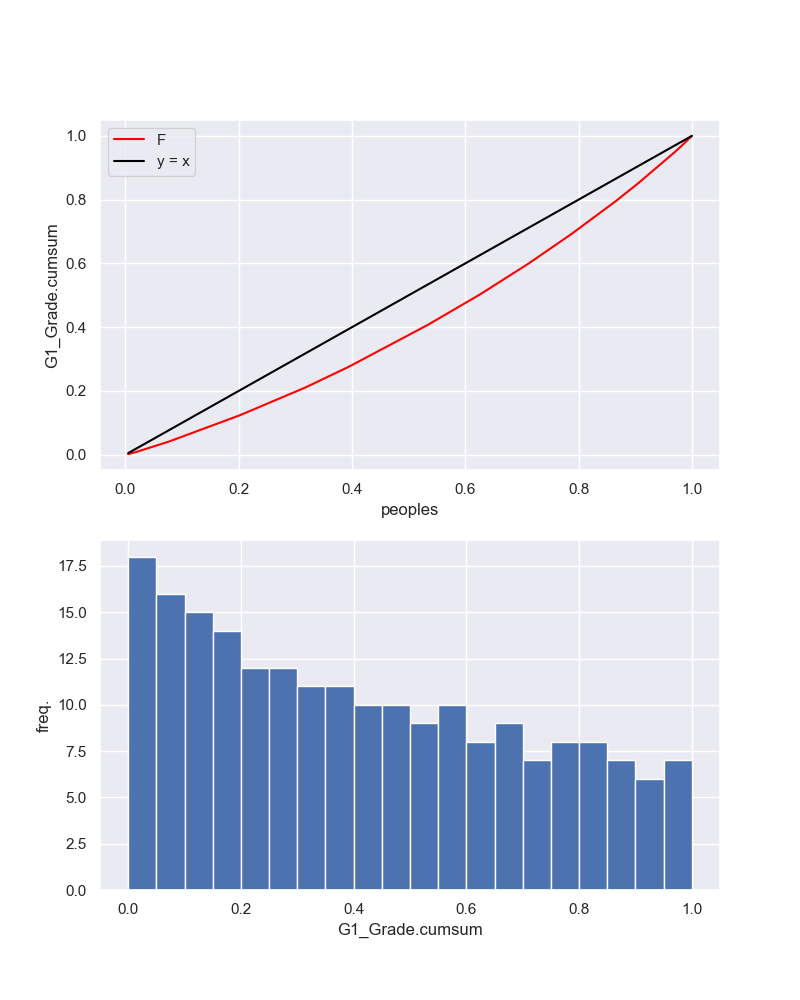
df0 = student_data_math[student_data_math['sex'].isin(['M'])] #F
df = df0.sort_values(by=['G1'])
df['Ct']=np.arange(1,len(df)+1)
x = df['Ct']
y1 = df['Ct']
# y2が得点の累積値
y2 = df['G1'].cumsum()
# y_int1はy=xの積分値
y_int1 = integrate.cumtrapz(y1/max(y1), x/max(x), initial=0)
# y_int2はG1の累積値の積分値
y_int2 = integrate.cumtrapz(y2/max(y2), x/max(x), initial=0)
# それぞれプロットします
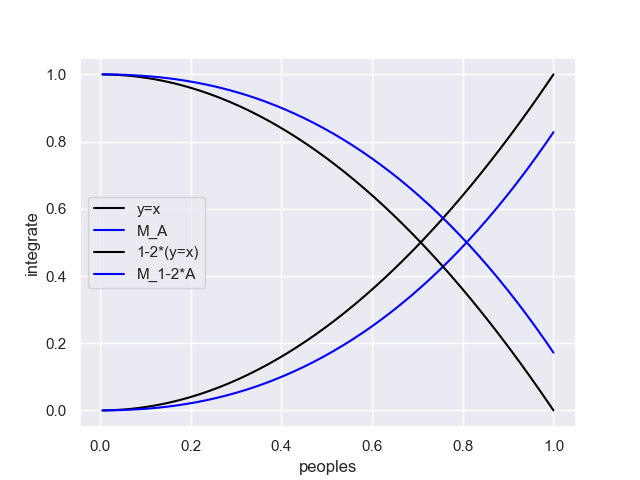
plt.plot(x/max(x), 2*y_int1,'black', label = 'y=x')
plt.plot(x/max(x), 2*y_int2, 'blue',label = 'M_A')
plt.plot(x/max(x), 1-2*y_int1,'black',label ='1-2*(y=x)')
plt.plot(x/max(x), 1-2*y_int2,'blue', label ='M_1-2*A')
plt.xlabel('peoples')
plt.ylabel('integrate')
plt.legend()
plt.show()
peaples=1の時の両者の差がGini係数です。
数値で見ると
print(1-2*y_int2[len(df)-1])
# 0.17198115609880305 M
# 0.17238700073127444 F
print(2*y_int1[len(df)-1])
# 0.999971403242873
です。
つまり、5桁目辺りに誤差がありそうですが、男女の差は4桁目にありそうです。女性の方が、少し大きいようです。
もう一つのGini係数求め方
\begin{align}
GI &=& \frac{\Sigma_{i=1}^{n}\Sigma_{j=1}^{n}|x_i-x_j|}{2\Sigma_{i=1}^{n}\Sigma_{j=1}^{n}x_j}\\
&=& \frac{\Sigma_{i=1}^{n}\Sigma_{j=1}^{n}|x_i-x_j|}{2n\Sigma_{i=1}^{n}x_i}\\
&=& \frac{\Sigma_{i=1}^{n}\Sigma_{j=1}^{n}|x_i-x_j|}{2n^2\bar x}\\
\end{align}
最初の式の導出はともかく、計算は以下のコードで実施できます。
xbar = df['G1'].mean() #平均値を求めます
s = []
s = df['G1'].loc[:].values #G1の値だけ取り出します
n = len(df) #人数を求めます
GI = 0
# 平均は男女で少し差があるようです
print(xbar) #10.620192307692308 F 11.229946524064172 M
for i in range(1,len(df),1):
a = s[i]
for j in range(1,len(df),1):
b = s[j]
GI += np.abs(a-b)
GI = GI/(2*n*n*xbar)
print(GI) #0.16938137688477206 F 0.16805449452508275 M
得られた数字は、相対的には同じ傾向ですが、上のいわゆる面積で求めたものと少し異なります。
・導出
やはり、まじめにこの方法の式の導出をしないといけないように思います。
まず、下の図の青い部分Aの面積を求める。
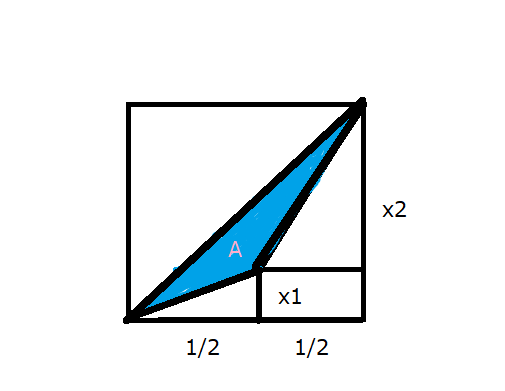
上の図で縦軸は規格化するので、x1, x2 は $x1⇒\frac{x1}{x1+x2}$, $x2⇒\frac{x2}{x1+x2}$ と読み替えてください。
そして、以下のような強引な式変形をすると、この2点の場合は、上のGini係数の式が成り立っているのが分かります。これを一般化すれば証明できそうですが、やる気しないので、またの機会にします。
\begin{align}
2*A&=2(1*1*1/2-1/2*\frac{x1}{x1+x2}*1/2-\frac{x1}{x1+x2}*1/2-1/2*\frac{x2}{x1+x2}*1/2)\\
&=\frac{2(x1+x2)}{2(x1+x2)}-\frac{x1}{2(x1+x2)}-\frac{2x1}{2(x1+x2)}-\frac{x2}{2(x1+x2)}\\
&=\frac{2(x1+x2)-x1-2x1-x2}{2(x1+x2)}\\
&=\frac{x2-x1}{2(x1+x2)}\\
&=\frac{|x2-x1|+|x1-x2|}{2*2^2\bar x}
\end{align}
※上の式変形を見ると、分母の$2n^2\bar x$は最初の2はi,jの和、次のnは平均、そしてもう一つのnは、横軸の間隔が1/nになるために出てきており、そもそも分母の$x1+x2$は縦軸の規格化のため出てきます。n個の場合も丁寧に計算すればこの台形公式で同じように導けそうです
それでは、なぜ数値に差が出たのかは分かりません。
まとめ
・Lorenz曲線とGini係数を求めてみた
・学生の成績分布を反映したGini係数が求められた
・男女間の得点分布差は小さい
・Gini係数の一般式を証明したいと思う
・株や為替、預貯金など投資効率(ポートフォリオ)に適用したいと思う