昨日に引き続いて、ドルコスト平均法のシミュレーションを突き詰めてみる。
要は、以下の結論がどうやって導き出せたのかを追求する
ドルコスト平均法の特徴
① 長期の定額投資でメリットがある
② 定額投資なので下がったときに口数が増加、上がったときは口数減少のため、利益が出やすい
①の長期が第一の疑問。そして定額投資にこだわる必要があるのか。
2の利益が出やすいは、どの程度出やすいのか知りたい。
というわけで、昨日のシミュレーションアプリを改変して、これらの疑問を解決しようと思う。
アプリの改変方針は、以下のとおり
・取得金額や時価を計算できるようにする
・期間による変化をグラフ表示する
・定額が必要なのか、投資額を変更できるようにして、実際に変更してゲインの多寡を見る
改変されたアプリの説明
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
import datetime as dt
from pandas_datareader import data
import yfinance as yf
import statsmodels.api as sm
from statsmodels.tsa.seasonal import STL
関数
以下は、前回同様、日付を取り扱う関数
from datetime import datetime
from datetime import timedelta
import random as rd
start = datetime.strptime('202104', '%Y%m').date()
end = datetime.strptime('202404', '%Y%m').date()
yosan0 = 3000
def daterange(_start, _end):
for n in range((_end - _start).days):
yield _start + timedelta(n)
株価変動を、今回は一様乱数などを使って、よりリアリスティックに出力する。また、市場の相場に応じて、購入金額も変更できるように関数で求めることとする。
rd.seed(a=7, version=2)
def market_make():
market = 20000 + 30000*rd.random()
return market
yosan0 = 3000 #1日あたりの凡その投資額
def yosan_make(market):
yosan = yosan0 #最初は一定額とする
return yosan
前回とほぼ同様だが、いくつか上記の探索するために変更している。
・平均取得費などを求める
・購入した株のその時点の時価を算出し、利益(earn)を求める
def market_history(start, end):
pd_stock = pd.DataFrame()
i_list = []
price_list = []
kutisu_list = []
kutisu_sum_list = []
cost_list = []
heikin_list = []
mean_price_list = []
total_cost_list = []
j=0
yosan_sum = 0
kutisu_sum = 0
price_sum = 0
for i in daterange(start, end):
market = market_make()
i_list.append(i)
price_list.append(market)
yosan = yosan_make(market)
kutisu = yosan / market
kutisu_list.append(kutisu)
cost_list.append(yosan)
yosan_sum += yosan
total_cost_list.append(yosan_sum)
kutisu_sum += kutisu
kutisu_sum_list.append(kutisu_sum)
heikin_list.append(yosan_sum/kutisu_sum)
price_sum += market
mean_price_list.append(price_sum/(j+1))
j +=1
pd_stock['date'] = i_list
pd_stock['price'] = price_list
pd_stock['kutisu'] = kutisu_list
pd_stock['kutisu_sum'] = kutisu_sum_list
pd_stock['cost'] = cost_list
pd_stock['total_cost'] = total_cost_list
pd_stock['heikin_cost'] = heikin_list
pd_stock['mean_price'] = mean_price_list
pd_stock['jika'] = pd_stock['price']*pd_stock['kutisu_sum']
pd_stock['earn'] = pd_stock['jika']-pd_stock['total_cost']
return pd_stock
pd_stock = market_history(start, end)
pd_stock[['price','total_cost','jika','heikin_cost', 'kutisu_sum', 'mean_price', 'earn']]
最後に、グラフ描画の関数。
fig, ax = plt.subplots(4,1)
ax[0].plot(pd_stock['price'])
ax[0].set_title('price')
ax[1].plot(pd_stock['kutisu'])
ax[1].set_title('kutisu')
ax[2].plot(pd_stock['mean_price'])
ax[2].set_title('mean_price')
ax[2].plot(pd_stock['heikin_cost'])
ax[2].set_title('heikin_cost')
ax[3].plot(pd_stock['jika'])
ax[3].plot(pd_stock['total_cost'])
plt.pause(1)
計算結果
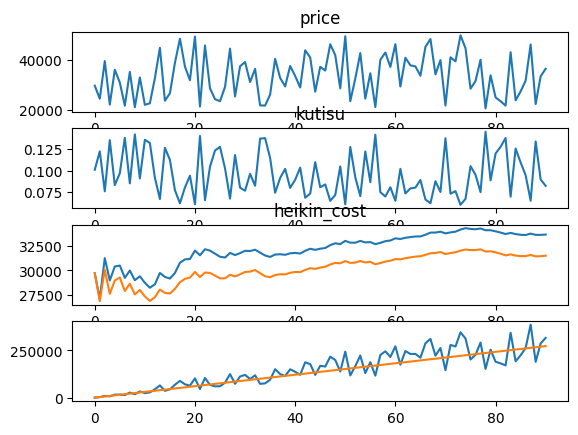
最初は、2024.1-2024.3末の様子
※株価;乱数
購入;一定額;毎日3000円
土日も売買してる設定だけド悪しからず
total_costを見ると最終的に273,000円購入して、43,164円儲かっている。
price total_cost jika heikin_cost kutisu_sum mean_price earn
0 29714.982945 3000 3000.000000 29714.982945 0.100959 29714.982945 0.000000
1 24525.475218 6000 5476.071610 26871.973523 0.223281 27120.229081 -523.928390
2 39528.034191 9000 11825.857354 30082.580658 0.299176 31256.164118 2825.857354
3 22173.088600 12000 9633.666163 27619.502140 0.434476 28985.395238 -2366.333837
4 36076.460129 15000 18674.341969 28978.097480 0.517632 30403.608217 3674.341969
... ... ... ... ... ... ... ...
86 31728.491094 261000 263198.307621 31463.485652 8.295330 33609.268760 2198.307621
87 46142.659224 264000 385768.590567 31577.640930 8.360346 33751.693652 121768.590567
88 22417.439036 267000 190417.543906 31433.323316 8.494170 33624.342476 -76582.456094
89 33475.622028 270000 287347.632982 31454.645559 8.583788 33622.690027 17347.632982
90 36483.197274 273000 316164.020417 31502.360208 8.666017 33654.124172 43164.020417
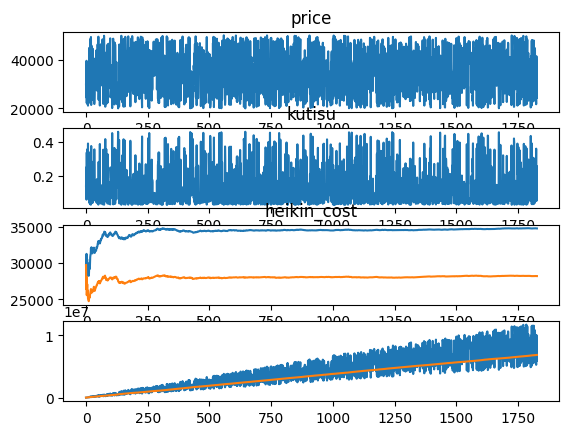
グラフ
グラフを見ると、株価が高いときは、口数が少なく、株価が安いときは口数多くなっており、その結果黄色い線(購入平均株価)が青い線(実際の単純平均株価)より下がっていることがわかる。その結果、最後の株価がこの黄色い線より高いことから、利益が出ているのがわかる。
今回は、乱数で35000円の上下で株価を出力しているので、平均コストは回数が増えると35,000円に収束しつつある。一方、取得単価はそれより約2,000円低い値に収束しつつあるのがわかる。
これがドルコスト平均法の重要な部分だ。
長期投資の効果
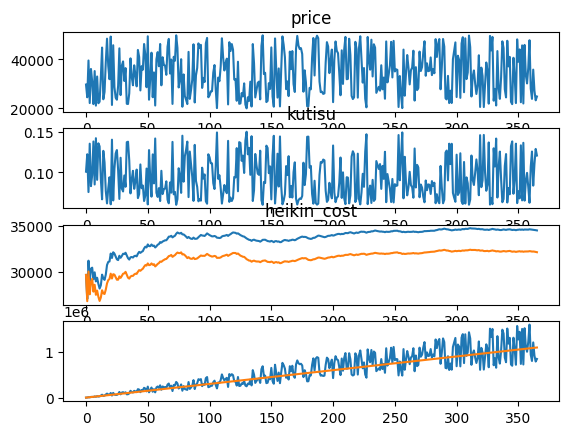
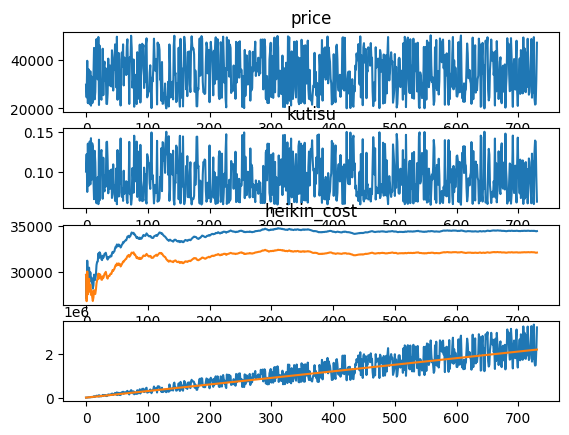
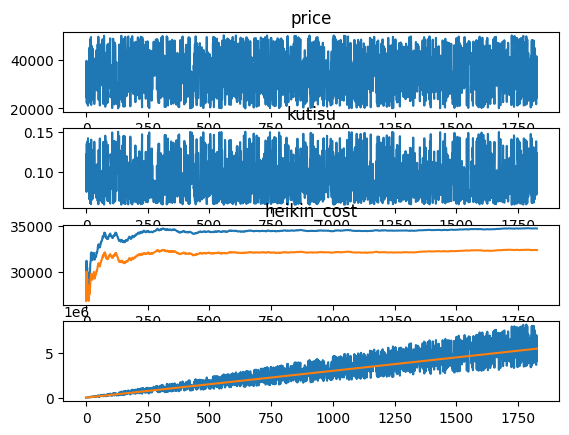
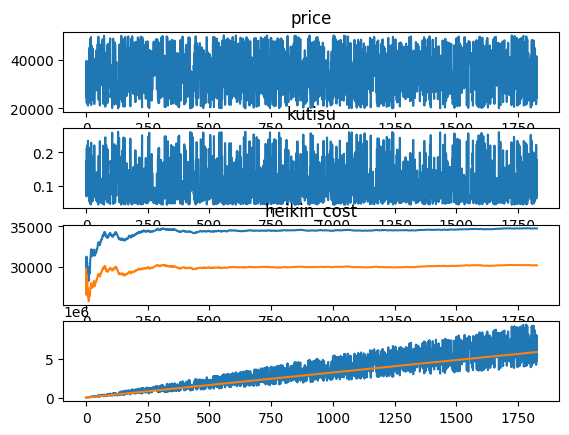
それでは、これを1年、2年、5年続けた場合のグラフを示す。
御覧のように徐々に平均取得額や平均株価が安定し、利益曲線も一定な振る舞いになる。ただし、重要なことは利益のグラフで黄色線は依然として日々の株価に連動して変動していることである。
もちろん、変動の中心よりは下側での変動なので、利益が出やすい状況ではある。
そして、長期投資の何よりのメリットは、利益の金額が大きくなっており、大きく利益を上げられる可能性が高くなっている。
※もちろん、短期を繰り返して一定の利益を上げ続けられれば同じだが、。。
利益の最適化
上記の場合、5年間の投資額
total_cost 5481000
実は、最後のグラフで黄色い線が青い帯の下側に来てくれれば、とにかく利益最大化も可能だ。
それを投資金額の制御でやってみた。
次の関数を弄る。
まず、株価が(名目的な平均株価より)下がったとき株価をより多く購入するために、予算をリニアに変える。
yosan0 = 3000
def yosan_make(market):
yosan = yosan0*(35000/market)
return yosan
投資額 5.918509e+06
count 1827.000000
mean 3239.468358
std 882.464846
min 2101.522546
25% 2465.755068
50% 3039.930210
75% 3887.072751
max 5248.593210
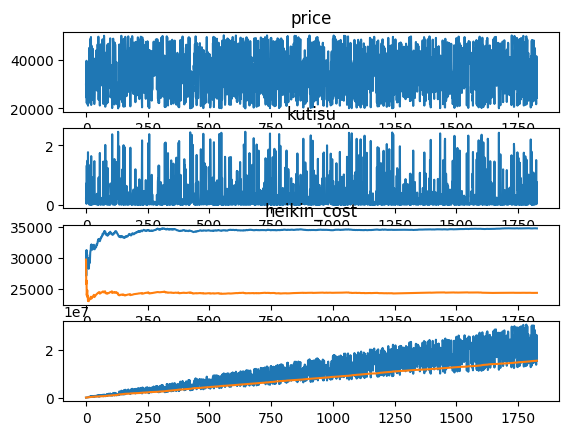
明らかに、黄色い線は下側に移動し、より利益を上げやすくなった。
同時に、平均取得額も30,000円を割って安くなっている。
yosan = yosan0*(35000/market)**2
平均取得額 28,202円
投資額 6.864936e+06
count 1827.000000
mean 3757.491069
std 2074.342571
min 1472.132337
25% 2026.649364
50% 3080.391893
75% 5036.444936
max 9182.576896
yosan = yosan0*(35000/market)**5
平均取得額 24,353円
pd_stock['cost'].describe()
投資額が3倍になってしまっているけど、。
※高い日は購入を控える感じです
total cost 1.550823e+07
count 1827.000000
mean 8488.356201
std 11268.570573
min 506.040469
25% 1125.290569
50% 3205.036998
75% 10955.403910
max 49173.322423
まとめ
・つまり、株価を監視して安いときに購入しろという普通の結論に到達する
・ドルコスト平均法だと、それを一応簡単な方法でシステムに任せられるメリットがある
・ドルコスト平均法で長期運用のメリットは、複利運用にあり、それもNISAという特別な制限での取引でメリットのある運用だと思う。このあたりの議論は次回にしたいと思う
・また、大体のコスト一定で投資コストの株価変動手法もとれるが、それは次回にしたいと思う
・実株価でのシミュレーションもできたので次回記載したい