 第十一夜は、ここが最重要ということで、今回は将棋AIの基礎となる理論を解説しようと思う。
※ここは最難関です。本書購入して、じっくり読んでいただくことを前提に端折ります
### 解説したいこと
(1)コンピュータ将棋のアルゴリズム
(2)コンピュータ囲碁のアルゴリズム
(3)AlphaGoの手法
### (1)コンピュータ将棋のアルゴリズム
ゲーム木とは、以下のようなものです。
つまり、自分の手番から順繰りにさせる手を追って、局面を進めていった可能な手順を作図したものです。ここで木の形状からゲーム木と呼びます。
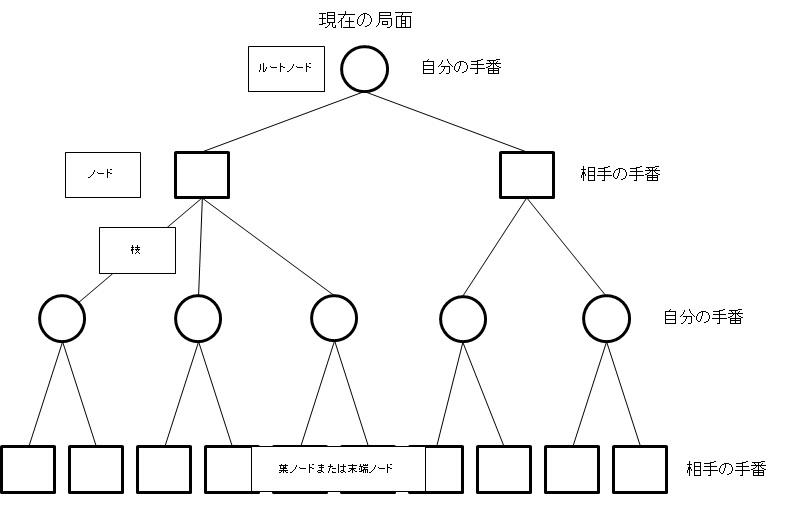
将棋などでは勝ちやすさをみるために各ノードの評価値を利用したミニマックス法が基本的な手法です。
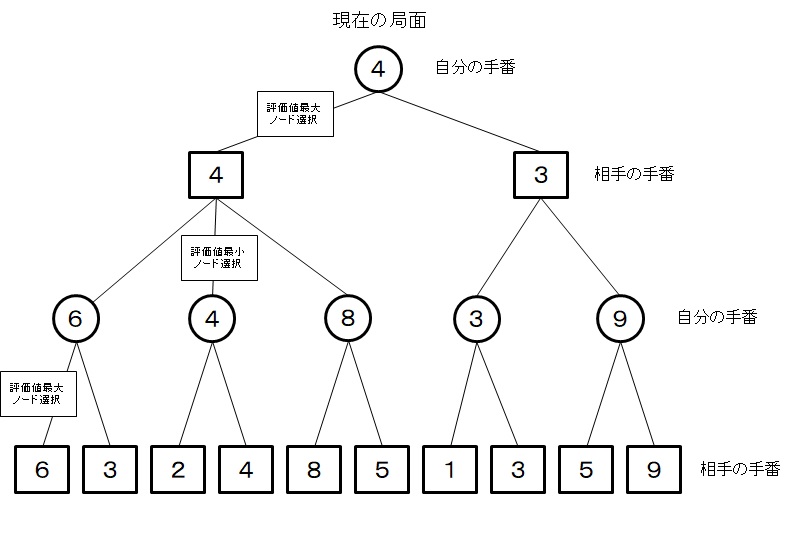
・まず、末端ノードの評価値は評価関数で求め、順に上のノードの評価値を以下の条件で求めます。
・自分の手番では相手の手番のノードの評価値最大を選択、相手の手番では自分の手番のノードの評価値最小を選択し、それぞれのノードの評価値とします。
・そして、ルートノードで選択したノードに対応する手を指し手とします。
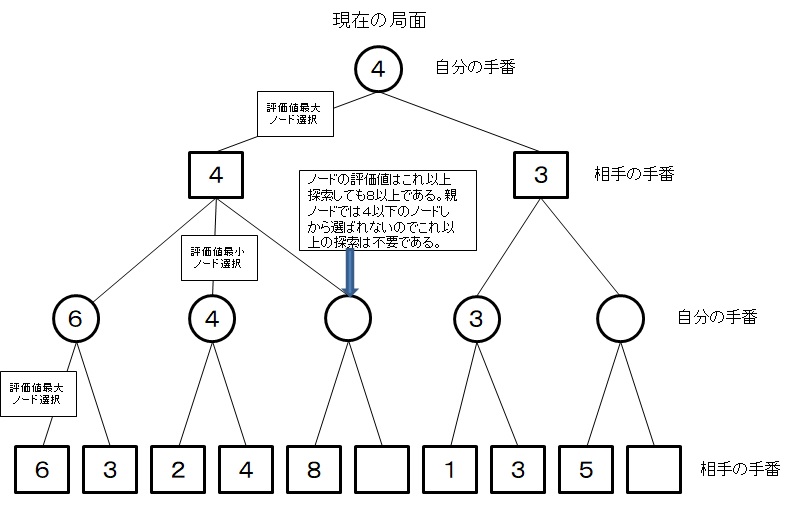
以下の図のように、調べている局面では、その子局面のうち評価値が最大の手が選択されるため、1つでも兄弟局面の評価値より大きい評価値がみつかれば、調べている局面が選択されることがなくなるため、それ以上の探索は省略できる。こうする手法をαβ法と呼び、現在の将棋AIはこの手法による探索が基本となっています。
#### 評価関数
局面の評価値を求める処理は評価関数で行います。
評価関数は
1.プログラマが将棋の知識を応用して評価関数を作成する
2.3駒関係を機械学習し、評価関数で使われるパラメータを調整する
第十一夜は、ここが最重要ということで、今回は将棋AIの基礎となる理論を解説しようと思う。
※ここは最難関です。本書購入して、じっくり読んでいただくことを前提に端折ります
### 解説したいこと
(1)コンピュータ将棋のアルゴリズム
(2)コンピュータ囲碁のアルゴリズム
(3)AlphaGoの手法
### (1)コンピュータ将棋のアルゴリズム
ゲーム木とは、以下のようなものです。
つまり、自分の手番から順繰りにさせる手を追って、局面を進めていった可能な手順を作図したものです。ここで木の形状からゲーム木と呼びます。

将棋などでは勝ちやすさをみるために各ノードの評価値を利用したミニマックス法が基本的な手法です。
・まず、末端ノードの評価値は評価関数で求め、順に上のノードの評価値を以下の条件で求めます。
・自分の手番では相手の手番のノードの評価値最大を選択、相手の手番では自分の手番のノードの評価値最小を選択し、それぞれのノードの評価値とします。
・そして、ルートノードで選択したノードに対応する手を指し手とします。

以下の図のように、調べている局面では、その子局面のうち評価値が最大の手が選択されるため、1つでも兄弟局面の評価値より大きい評価値がみつかれば、調べている局面が選択されることがなくなるため、それ以上の探索は省略できる。こうする手法をαβ法と呼び、現在の将棋AIはこの手法による探索が基本となっています。

#### 評価関数
局面の評価値を求める処理は評価関数で行います。
評価関数は
1.プログラマが将棋の知識を応用して評価関数を作成する
2.3駒関係を機械学習し、評価関数で使われるパラメータを調整する
(2)コンピュータ囲碁のアルゴリズム
囲碁の課題
・探索空間が広い(局面;10^360)
・評価関数を作るのが難しい(白黒なので)
モンテカルロ木探索
1.選択
図の分数;分母;訪問回数、分子;報酬
報酬は、プレイアウトを行った結果として勝った場合1の報酬が、たどってきた各ノードに与えられます。
図の分数に基づいて、ミニマックス法を適用します。

2.展開
訪問回数が閾値より大きい場合、候補手でゲーム木を展開します。展開した後、いずれかのノードを選択し、プレイアウトステップに進みます。訪れたノードの訪問回数が閾値未満の場合、展開を行わず次のプレイアウトのステップに進みます。

3.プレイアウト
ゲーム木の末端までたどって、そのノードの訪問回数が閾値以下の場合、そのノードからプレイアウトを行います。
4.バックアップ
プレイアウトを行った結果の勝敗を報酬として、たどってきたノードに報酬を加算します。報酬は、勝ちの場合は1、負けの場合は0とします。また、たどってきた各ノードの訪問回数に1を加算します。

以上4つの手順を、思考時間内に何回も行い、最終的にルートノードでの訪問回数が最も多い手を打ち手としては選択します。
選択のステップで、勝率に応じてノードを選択するが、勝率が最も高い手を選ぶだけでは、最初に選んだノードでプレイアウトの結果が負けだった場合、そのノードの勝率は0となり、以後選ばれなくなる。そのため、探索回数が少ないノードは勝率が低くても探索してみる必要がある。一方で、その分有望な手の探索回数が減少するので、両者はトレードオフの関係にあり、「活用と探索のジレンマ」と呼ばれる問題だそうです。
囲碁AIでは、ノード選択のアルゴリズムにUCB1というアルゴリズムが使われており、UCB1を用いたモンテカルロ木探索のことを、UCTアルゴリズムと呼んでいるそうです。
AlphaGoで用いられている探索方法もUCTがもとになっています。
マルチアームドバンディッド問題
※ググって参考にしようとしたが、本書の記載が簡単でしたが、それをさらに端折ります
問題
「n本のレバーがあるスロットマシンがあります。コインを投入していずれかのレバーを引くと、あたりの場合は賞金が得られます。レバーごとに得られる賞金は異なります。期待値は事前にはわかりません。あなたは手元にある枚数のコインを持っています。得られる賞金を最大化するにはどのようにレバーを選択すればよいでしょう。」
レバーを選択すること;行動(Action)
賞金;報酬(賞金)
賞金の期待値;価値(Value)
単純な戦略
「すべてのレバーに一定の枚数ずつ投入して、その結果期待値が最も高かったレバーに残りのコインを投入する」
これだと、最初の期待値が少ないレバーに入れたコインがもったいない。
UCB1アルゴリズム
UCB1アルゴリズムは、
「コインを投入するたびに以下の式の値が最大なレバーjを選択する。」
\bar{x}_j+\sqrt{\frac{2\log{n}}{n_j}}
ここで
\bar{x}_j ;レバーjで得られた報酬の平均
n_j ;レバーjを選択した回数
n ;コインを投入した合計回数
この式は、(期待値項+ボーナス項)という構造であり、期待値項はこれまでに得られた報酬の期待値を表し、ボーナス項はコインを投入した枚数が少ないレバーほど選択されやすくすることを示しています。
UCTアルゴリズム
UCB1アルゴリズムをモンテカルロ木探索のノード選択に用いた探索アルゴリズムをUCTアルゴリズムと呼びます。
マルチアームドバーンディッドとUCTアルゴリズムは以下のように対比できます。
| ー | マルチアームドバーンディッド | UCTアルゴリズム |
|---|---|---|
| 期待値 | 賞金の期待値 | 勝敗の期待値 |
| 選択 | レバー選択 | ノードでの手選択 |
| 1.選択 | ||
| ミニマックス探索と同様に、ルートノードからゲーム木を未展開のノードに達するまでたどります。各ノードでは、UCB1アルゴリズムに従って、有望なノードを選択します。相手番のノードでは、自分の番での勝率が最小になるノードが選ばれるようにします。 | ||
| 2.展開 | ||
| 未展開のノードに達したら、訪問回数が閾値より大きい場合、その局面の合法手を打った後の局面を表す子ノードを追加します。 | ||
| 3.プレイアウト | ||
| ゲーム木をたどって達した末端ノードの訪問回数が閾値以下の場合、その局面からプレイアウトを行います。 | ||
| 4.バックアップ | ||
| プレイアウトを行った結果の勝敗を報酬として、たどってきたノードに加算します。報酬は勝ちは1、負けは0です。また、たどってきた各ノードの訪問回数に1を加算します。 |
UCTアルゴリズムにおけるノード選択の例は以下のとおりです。

上記の例の場合、番号を入れたノード1~3のそれぞれのUCB1の値は以下の表のとおりです。
| 1 | UCB1 | 値 |
|---|---|---|
| ノード1 | 1式 | 1.45 |
| ノード2 | 2式 | 1.26 |
| ノード3 | 3式 | 2.18 |
\frac{7}{10}+\sqrt{\frac{2\log{17}}{10}}≒1.45 (1)
\frac{1}{5}+\sqrt{\frac{2\log{17}}{5}}≒1.26 (2)
\frac{1}{2}+\sqrt{\frac{2\log{17}}{2}}≒2,18 (3)
※ノード3からプレイアウトします
この手順を思考時間内に複数回実施し、最終的にルートノードでの訪問回数が最も多い手を打ち手として選択します。選択のステップ以外はモンテカルロ木探索と同じです。
UCB1アルゴリズムは実際には定数Cを使用して
\bar{x}_j+C\sqrt{\frac{2\log{n}}{n_j}}
が利用されます。定数Cは理論的には1ですが、実際はプログラムが一番強くなるように調整されます。
(3)AlphaGoの手法
モンテカルロ木探索を強くする方法
・優先順位制御の改善
UCTアルゴリズムのノード選択において、有望な手を優先し、無駄な手を調べないようにすること。
・プレイアウトの質の改善
着手の精度を高めること。プレイアウトは終局までプレイするため、着手処理の回数が多く、高速に動作することが求められる。大きいパターンサイズだと、着手予測の精度は高まるが、実行時間がかかる。小さいパターン(3x3など)では判断が局所的になります。
AlphaGoでは方策ネットワークと価値ネットワークと呼ぶニューラルネットワークを使うことで、優先順位制御とプレイアウトの質の2つを大幅に改善することに成功しました。
AlphaGoでは、方策ネットワークをモンテカルロ木探索の各ノードのノード選択の優先順位付けに使用しています。方策ネットワークによる着手予測が高い手に絞って探索をします。方策は、ある局面でどの手を選択するかの確率分布p(a|s)を与える関数になります。
AlphaGoでは事前に学習した価値ネットワークと並列にロールアウトポリシーと呼ぶ3x3パターンなどを使った軽量の方策を使ってプレイアウトを行った結果との平均を価値としているそうです。そして、AlphaGo zeroではロールアウトポリシーを使わず価値ネットワークのみで局面を評価しているそうです。
AlphaGoの探索アルゴリズム
1.選択
ルートノードからゲーム木を未展開のノードに達するまでたどります。各ノードでは以下の式が最大になる手を選択します。
Q(s_t,a)+U(s_t,a)
Q(s_t,a);状態s_tにおける行動aの行動価値\Rightarrow 期待値項
U(s_t,a);探索回数が少ない手を探索回数が多い手よりも優先するための値を制御\Rightarrow ボーナス項
s_t;現在のノードの状態(局面のこと)
s;状態s_tで選択できる行動(候補手のこと)
U(s,a)=c_{puct}P(s,a)\frac{\sqrt{\sum_bN(s,b)}}{1+N(s,a)}
ここでP(s,a)は方策ネットワークにより予測した着手確率を使用する。
c_{puct};ボーナス項の重み調整
N(s,a)は状態sにおける行動aの訪問回数
\sum_bN(s,b);状態sにおけるすべての行動の合計訪問回数
つまり、この式は方策ネットワークによる着手予測が高い手を優先することとまだ訪問回数が少ない手を優先することを意味します。
2.評価
末端ノードに達した場合、そのノードが未評価の場合、価値ネットワークにより局面の評価を行います。AlphaGoでは価値ネットワークの計算中に並列でロールアウトポリシーを使用して複数回プレイアウトを行います。
3.バックアップ
評価の結果をたどってきた各ノードに反映します。
以下の式でQ(s,a)を計算します。
Q(s,a)=(1-\lambda)\frac{W_v(s,a)}{N_v(s,a)}+\lambda\frac{W_r(s,a)}{N_r(s,a)}
ここで前項は価値ネットワークで求めた勝率の平均、後項はロールアウトによって得られた報酬の平均で、λは平均の重みです。AlphaGoの論文ではλ=0.5のとき一番強くなっています。
4.展開
末端ノードの訪問回数が閾値より大きい場合、そのノードにすべての合法手を打った後の局面を表す子ノードを追加します。追加した子ノードが保持する値を初期化します。
まとめ
・将棋AIの理論として主要な戦略をまとめました
・最後はAlphaGoの探索アルゴリズムをまとめました
・これでAlpha Zeroの探索アルゴリズムの導入の準備ができました