今回は、前回の時系列分解をさらに追及してみた。
すなわち、モデルは以下のとおり
$Y_t=T_t + S_t + e_t$
または、
$Y_t=T_tS_te_t$
として、時系列データを分解するdecompose()手法である。
前回は、それぞれのデータを同時描画していたが、今回は例えばノイズ除去した純粋な音声や振動などの再生や利用を目的に、それぞれ保存したり再生したいという動機から実施してみた。
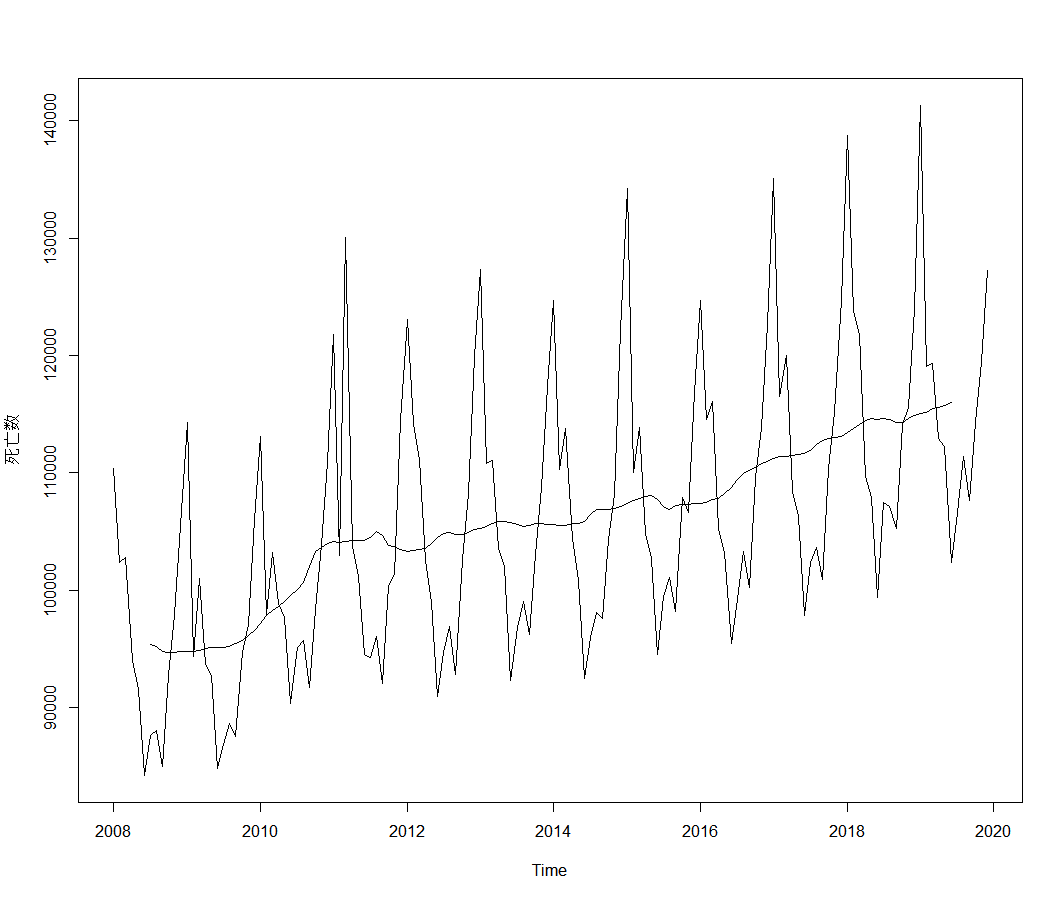
データは参考③のサイトの死亡数の速報値と参考④の2018年までの過去データである。
今回の参考は以下のとおりである。
参考①はR言語のものであり、参考②はpythonのものである。
ここでは独立に数値化してcsvファイルに保存するまでをまとめる。
【参考】
①Extracting Seasonality and Trend from Data: Decomposition Using R
②TIME SERIES DECOMPOSITION & PREDICTION IN PYTHON
③統計で見る日本 e-Statは、日本の統計が閲覧できる政府統計ポータルサイトです
④データセット一覧(5-4死亡月別にみた年次別死亡数及び死亡率(人口千対))@統計で見る日本
なお、今回のコードとデータは以下に置きました。
・MuAuan/R_Audio
やったこと
・Rでのdecompose
・pythonでのdecompose
・Rでのdecompose
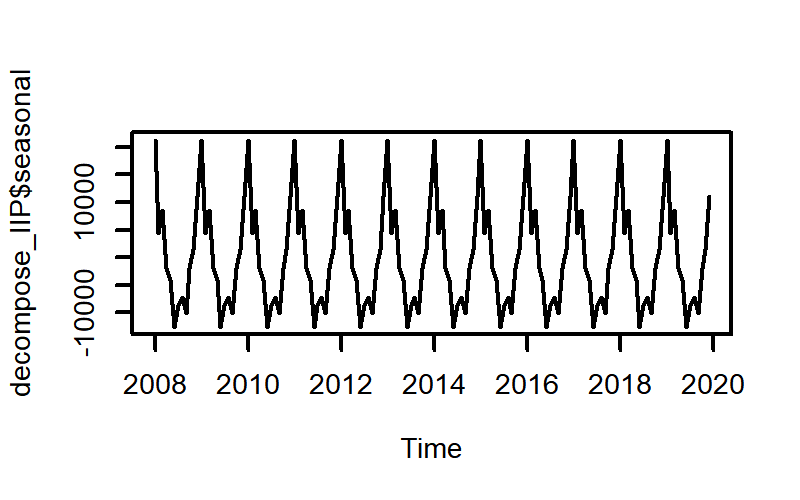
前回のほぼまんまですが、decompose_IIP$seasonalという表記でseasonalのデータを指定できます。
data <- read.csv("./industrial/sibou_p.csv",encoding = "utf-8")
IIP <- ts(data,start=c(2008),frequency=12)
w_list <- c("seasonal","random","trend","observed")
decompose_IIP <- decompose(IIP)
for (i in w_list){
if (i=="seasonal"){
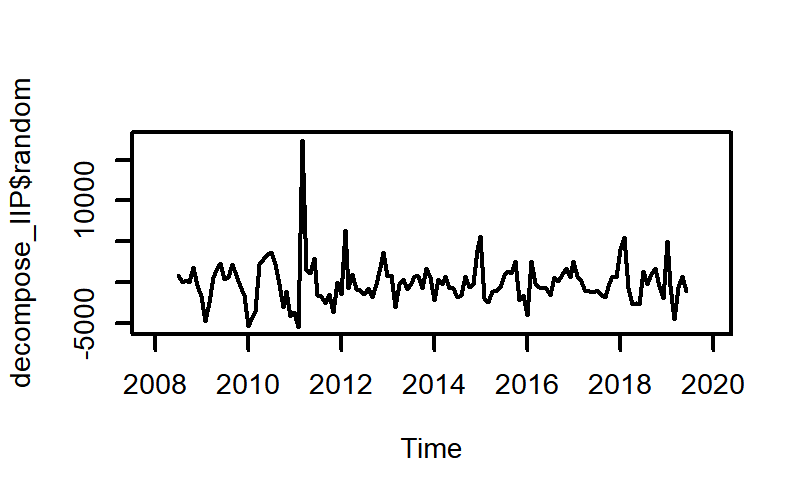
plot(decompose_IIP$seasonal)
}else if(i=="random"){
plot(decompose_IIP$random)
}else if(i=="trend"){
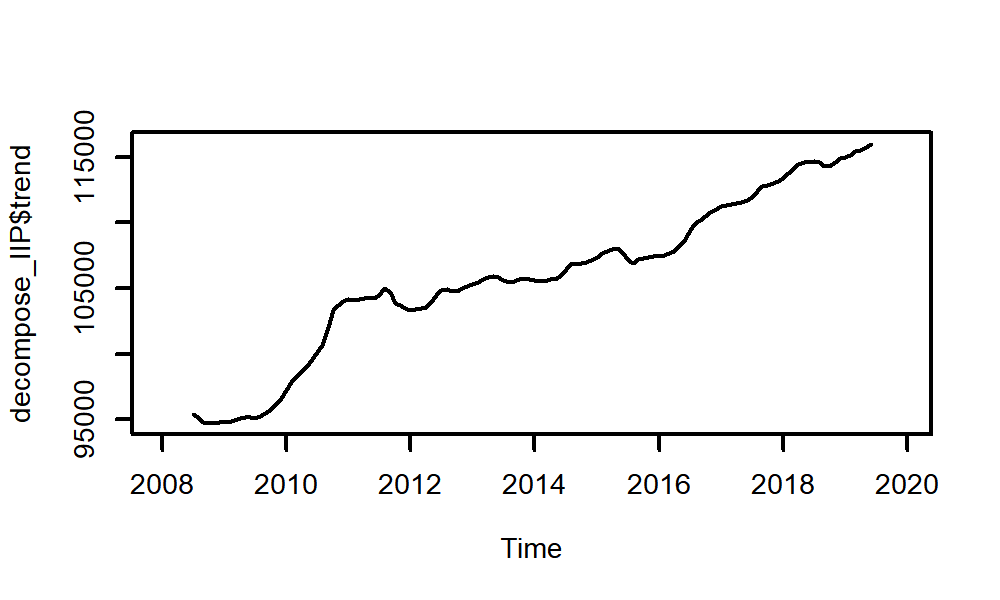
plot(decompose_IIP$trend)
}else if(i=="observed"){
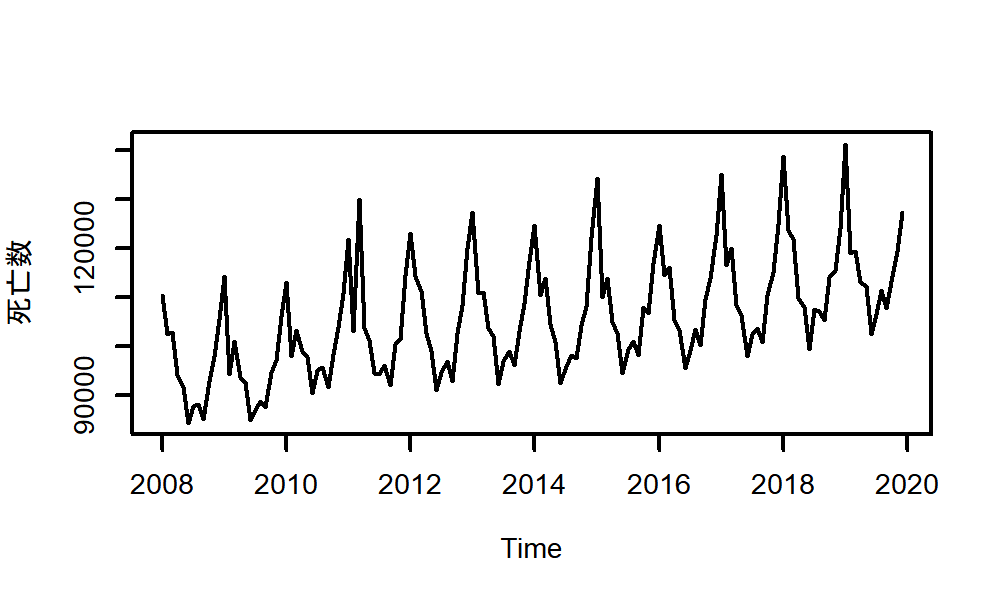
plot(IIP)
}
}
| seasonal | random |
|---|---|
 |
 |
| trend | observed |
 |
 |
| もう一つのコード | |
| まず、オリジナルデータを描画します。 | |
| 次に、今回のデータは12か月周期なのでトレンド曲線として12移動平均を取ります。 | |
| そして、上記のオリジナルデータに重畳してlinesを引きます。 |
# install.packages("forecast")
library(forecast)
plot(as.ts(IIP))
trend_beer = ma(IIP, order = 12, centre = T) #4
lines(trend_beer)
plotはそのトレンド曲線だけを描画しています。
plot(as.ts(trend_beer))
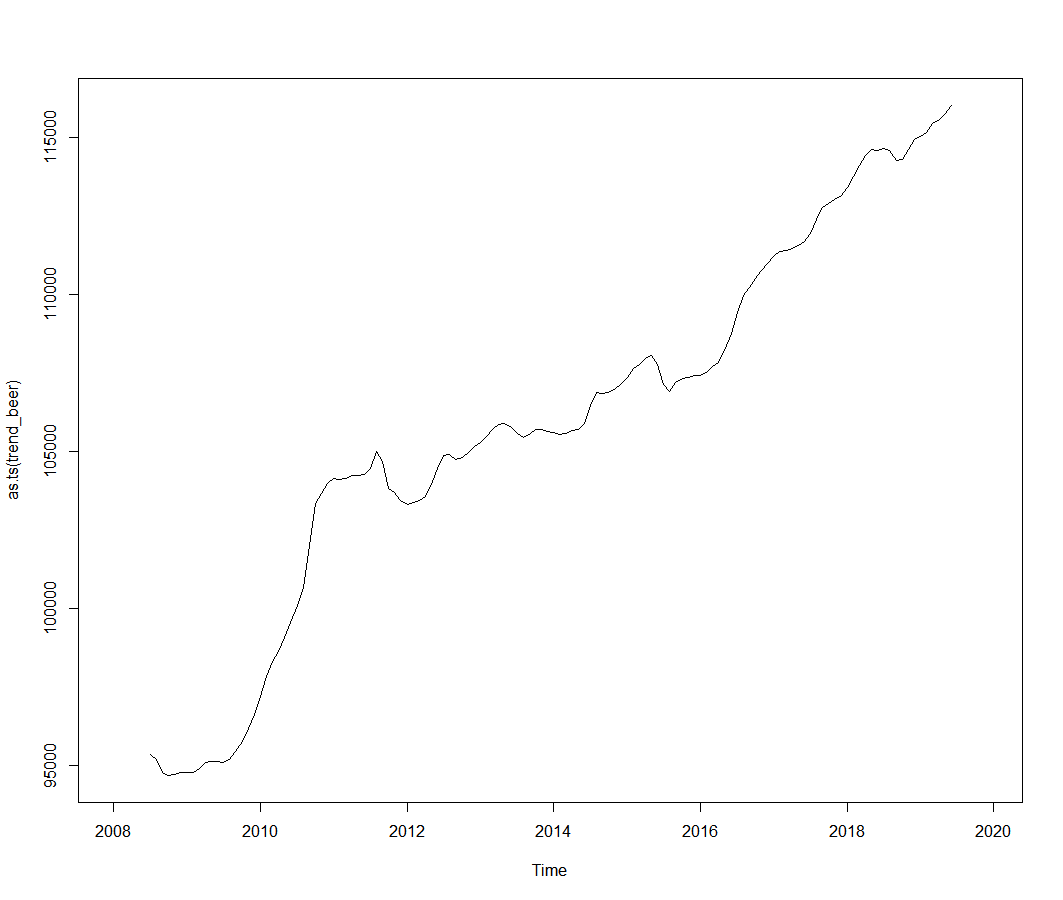
オリジナルデータからトレンドデータを引き算してプロットします。
detrend_beer = IIP - trend_beer
plot(as.ts(detrend_beer))
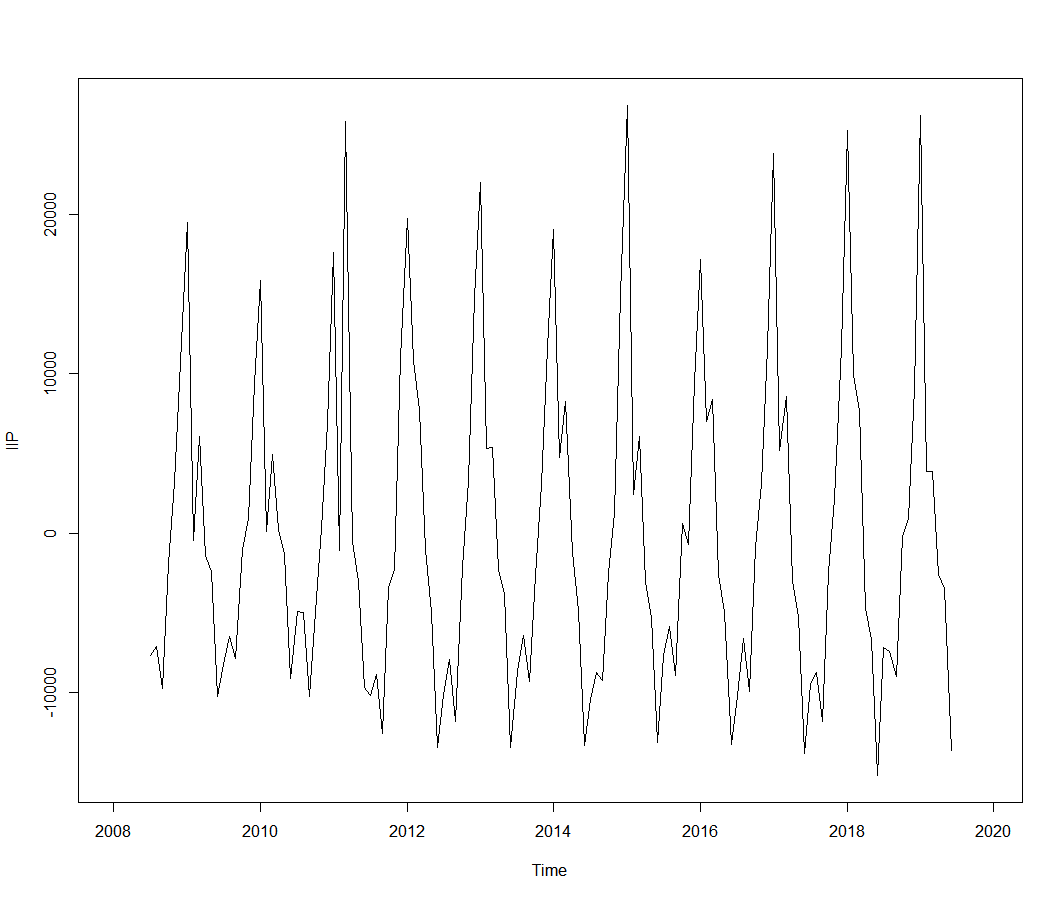
そして、トレンドを差し引いたノイズが乗っているデータを12個ずつのデータに区分して、それらを平均したものを季節変動として計算します。
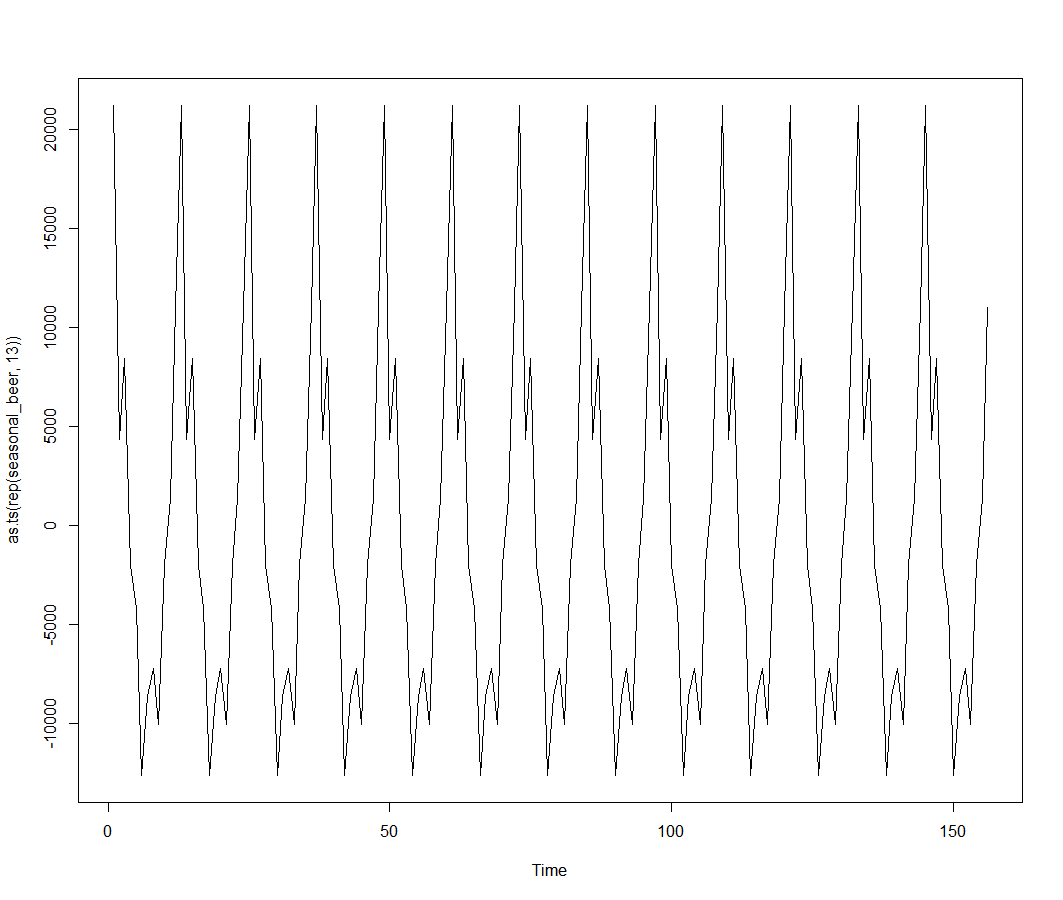
それを13個連ねて描画しています。
【参考】
・Row and Column Summaries
・matrix
m_beer = t(matrix(data = detrend_beer, nrow = 12))
seasonal_beer = colMeans(m_beer, na.rm = T)
plot(as.ts(rep(seasonal_beer,13)))
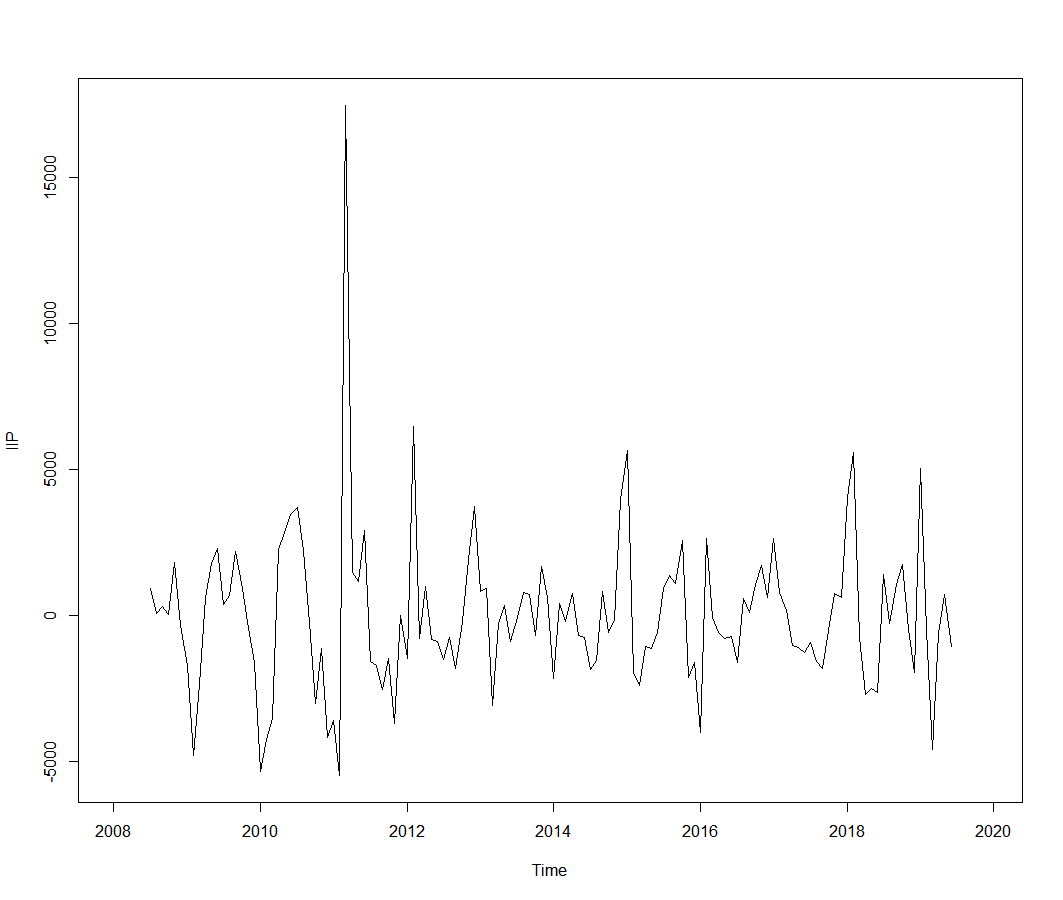
最後に、ランダムな変動分を求めます。
結果はdecompose()関数で求めたものと一致しました。
こんな計算で求めているんですね。
random_beer = IIP - trend_beer - seasonal_beer
plot(as.ts(random_beer))
最後にいろいろ利用するために、以下のようにcsvファイルに出力します。
write.csv(as.ts(rep(seasonal_beer,1300)), file = 'decompose_seasonal1300.csv')
・pythonでのdecompose
pythonでも同じような関数が用意されています。
コードは以下のとおりです。
import pandas as pd
import statsmodels.api as sm
from statsmodels.tsa.seasonal import STL
import matplotlib.pyplot as plt
# Set figure width to 12 and height to 9
plt.rcParams['figure.figsize'] = [12, 9]
df = pd.read_csv('sibou_.csv')
series = df['Price']
print(series)
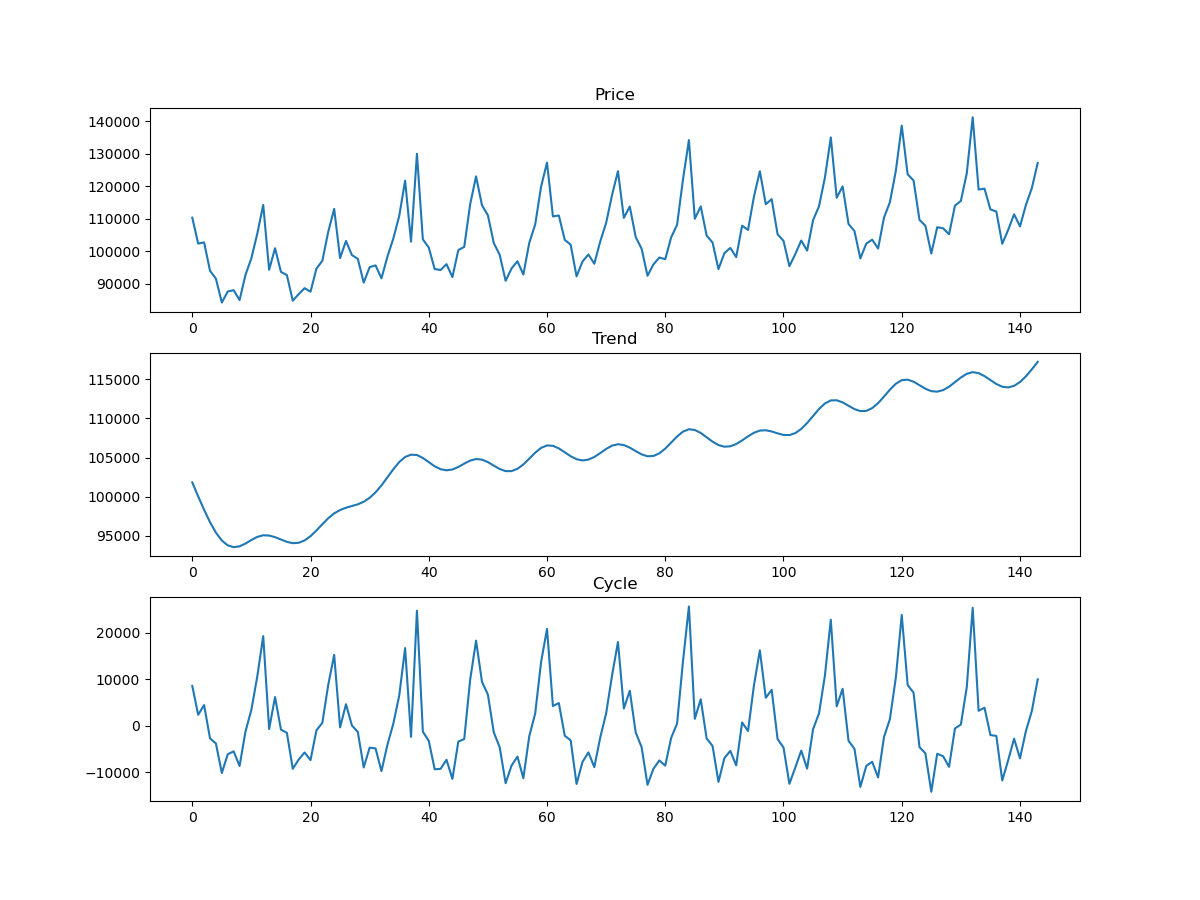
cycle, trend = sm.tsa.filters.hpfilter(series, 144)
fig, ax = plt.subplots(3,1)
ax[0].plot(series)
ax[0].set_title('Price')
ax[1].plot(trend)
ax[1].set_title('Trend')
ax[2].plot(cycle)
ax[2].set_title('Cycle')
plt.show()
pythonでももう一つの方法
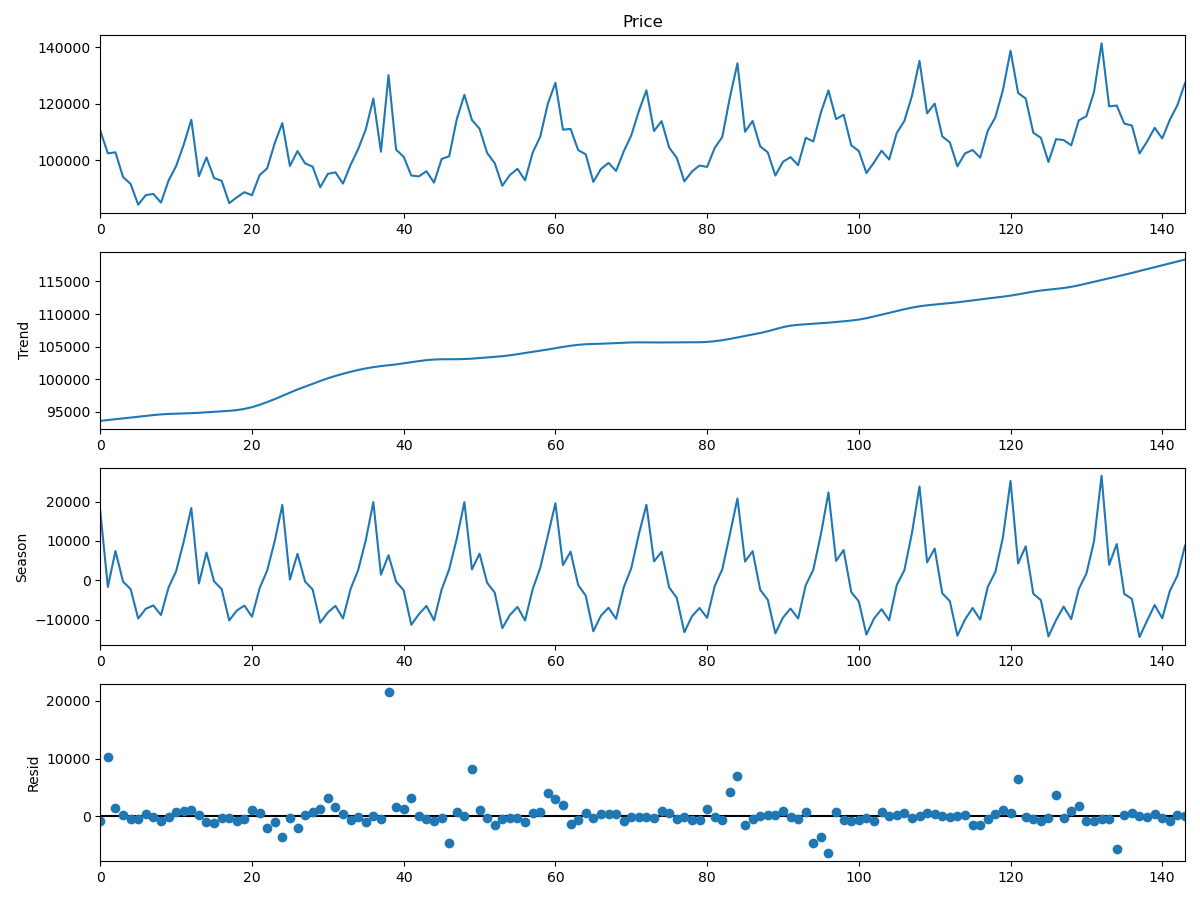
個人的には、分解の結果は上の方法だとcycleに対してもう一段の処理が必要で、こちらはランダム分の処理までできているのでこちらの方がリーズナブルに見えます。
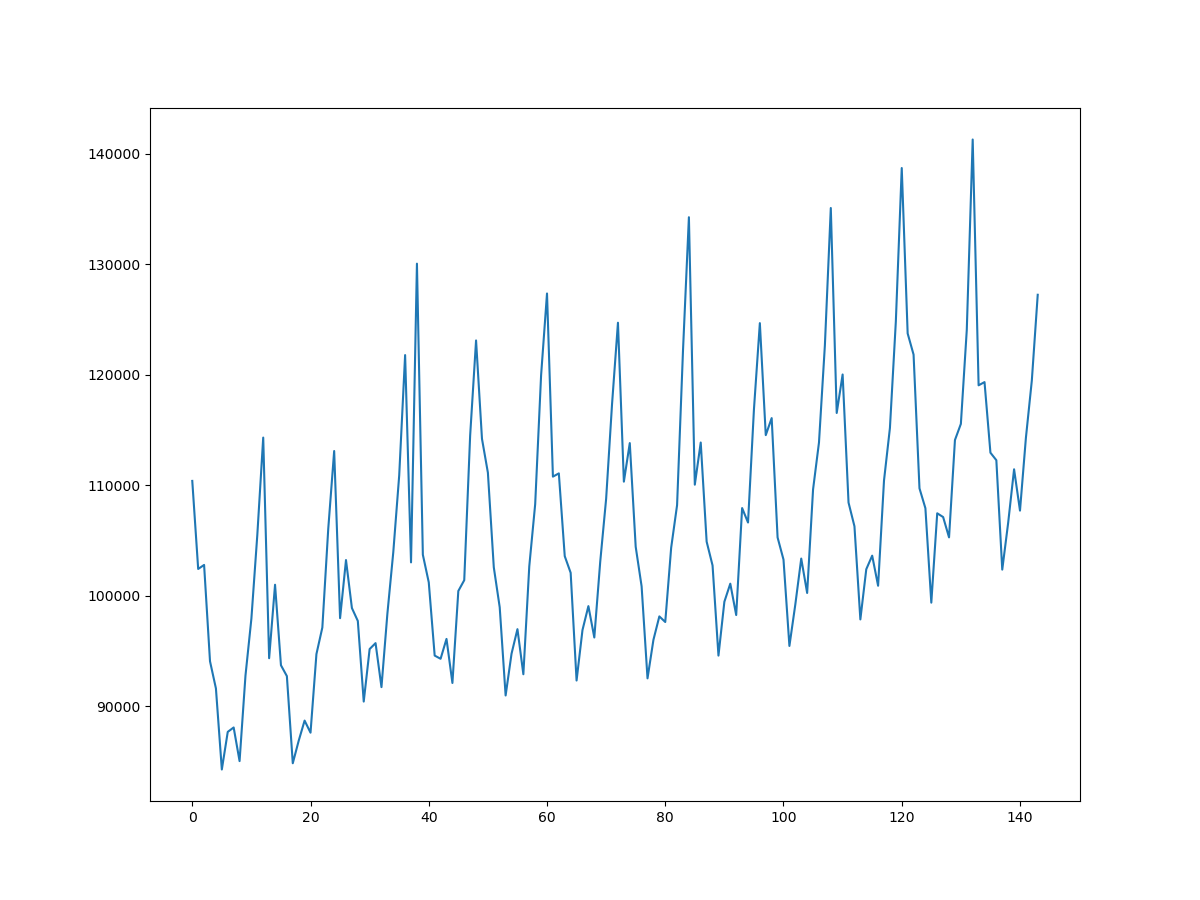
また、Rと比較しても、少し異なりseasonalは年々振動幅が大きくなっている様子を見せています(Rはこの変動を平均化処理したので消えているのは当たり前ですが。。。)。場合により、この手法が一番汎用性が高いと言えると思います。
【参考】
・Seasonal-Trend decomposition using LOESS (STL)
stl=STL(series, period=12, robust=True)
result = stl.fit()
chart = result.plot()
chart1= result.plot(observed=False, resid=False)
chart2= result.plot(trend=False, resid=False)
plt.show()
Observed & Trend & Seasonal & Residual
Trend & Seasonal
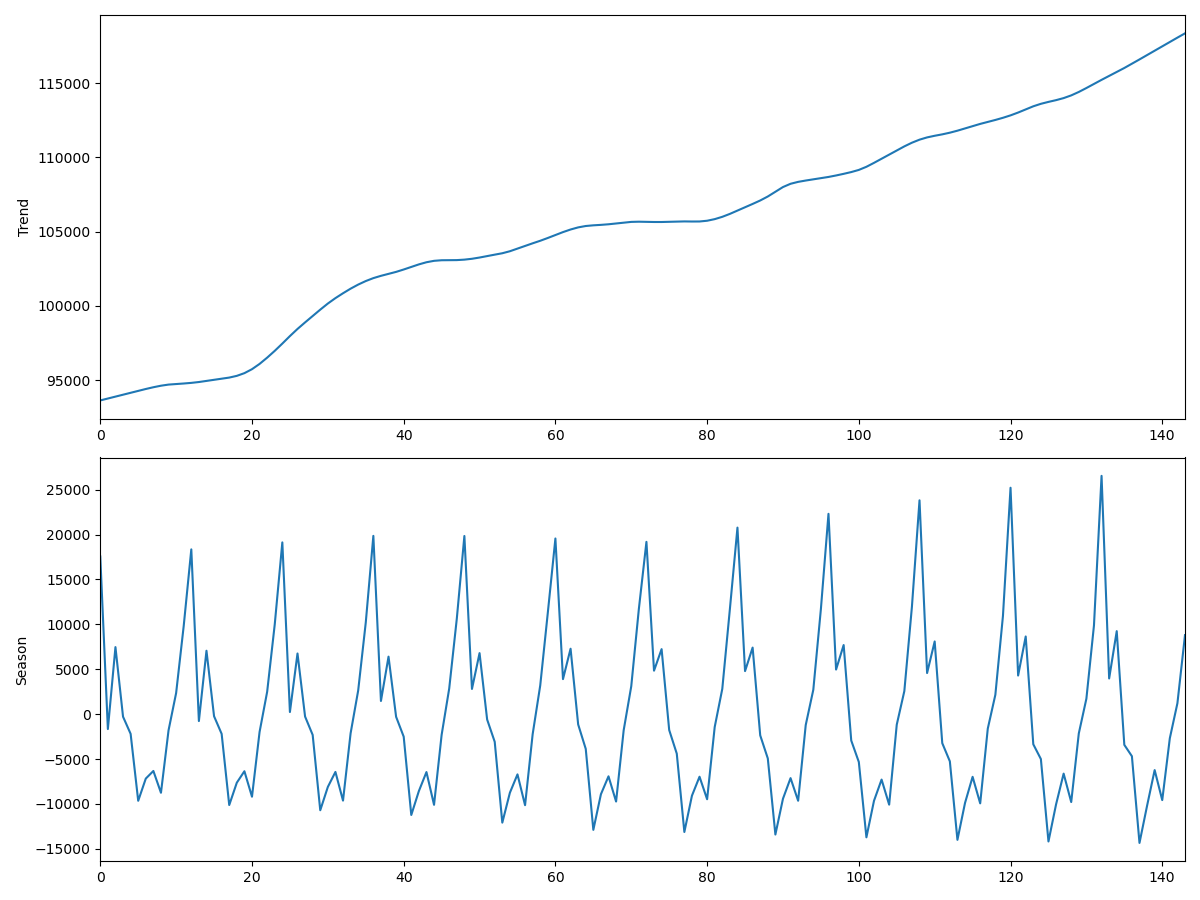
Obeserved & Seasonal
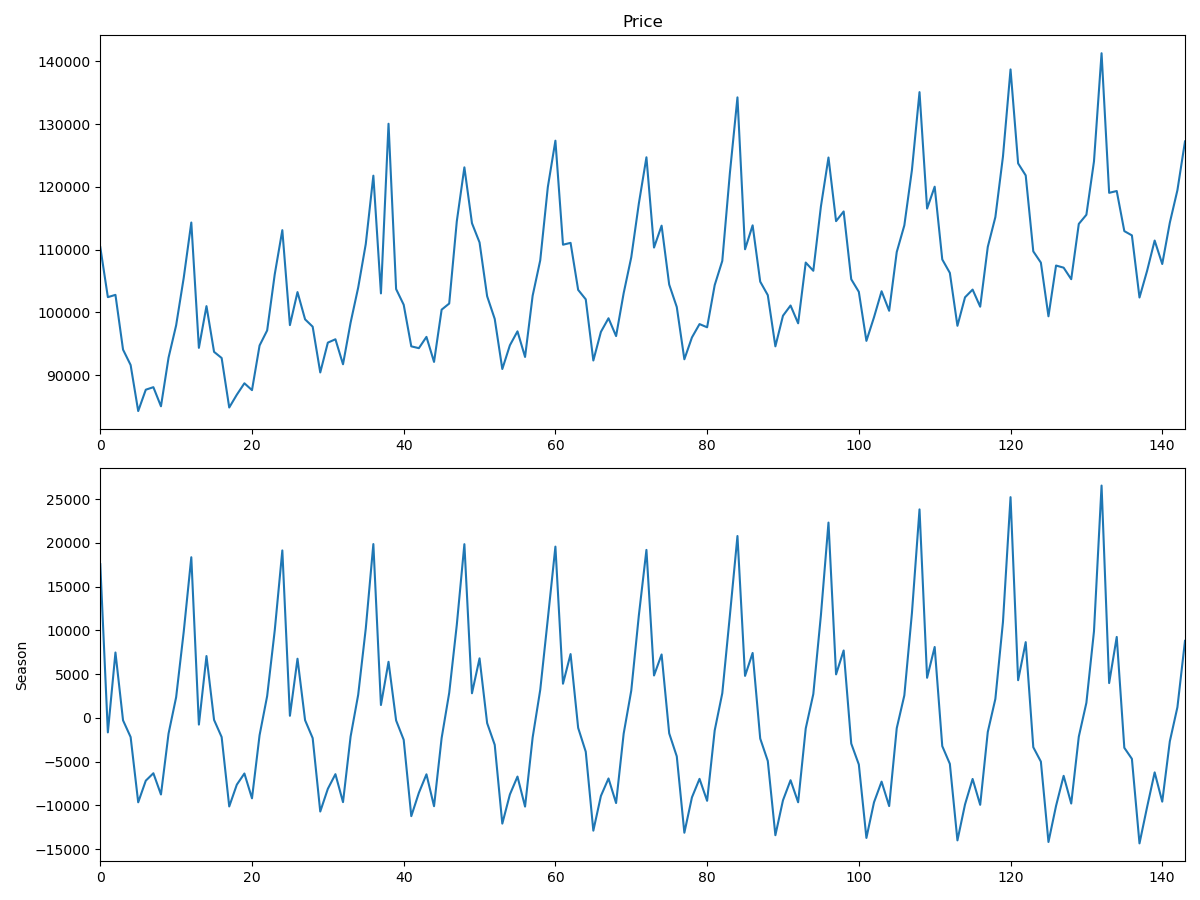
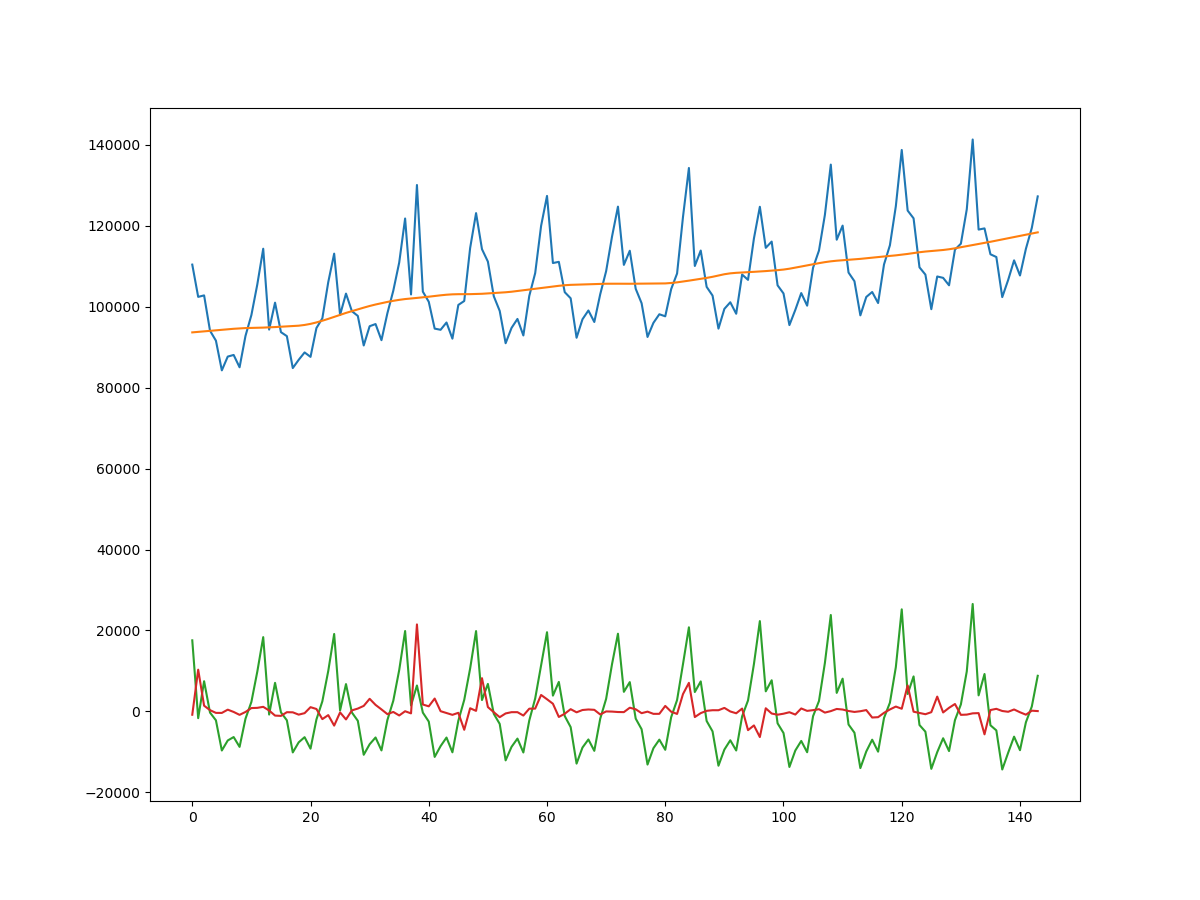
また、以下のようにすると、ばらばらのグラフとして一つのグラフに出力できます。
※pl1...などの数値データを利用するため変数に代入しています
pl1 = result.observed
pl2 = result.trend
pl3 = result.seasonal
pl4 = result.resid
plt.plot(pl1)
plt.plot(pl2)
plt.plot(pl3)
plt.plot(pl4)
plt.show()
plt.close()
また、以下のようにすると簡単に出力できます。
pl5 = result.seasonal.plot()
plt.show()
plt.close()
...
| seasonal | resid |
|---|---|
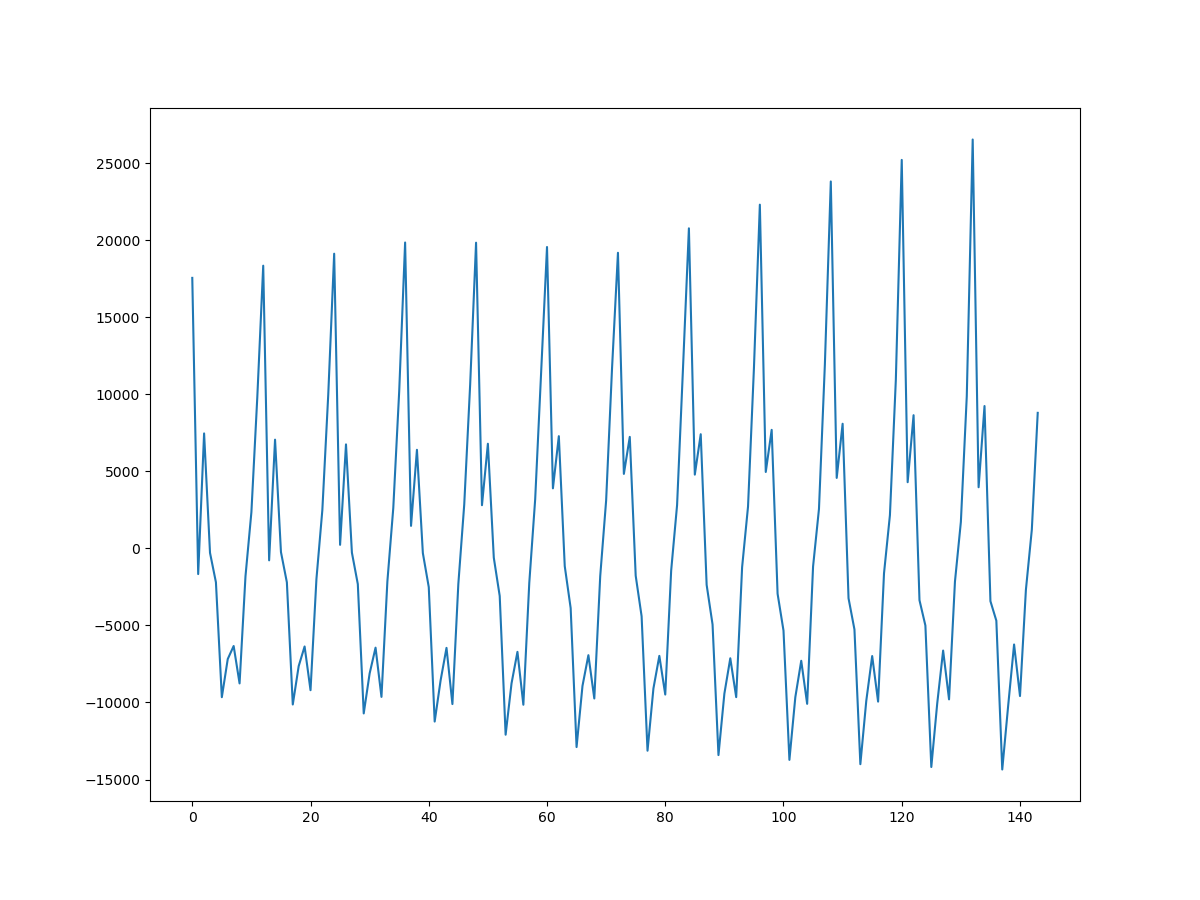 |
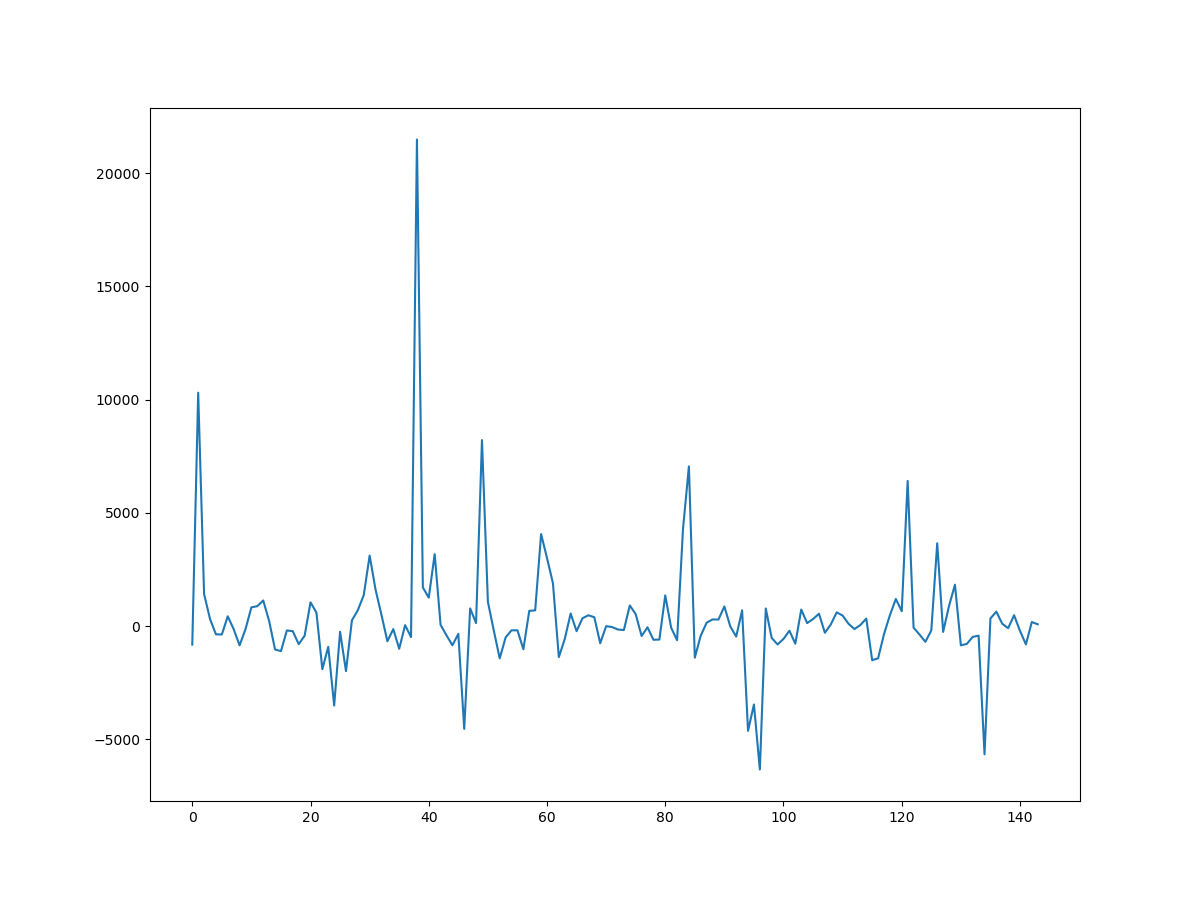 |
| trend | observed |
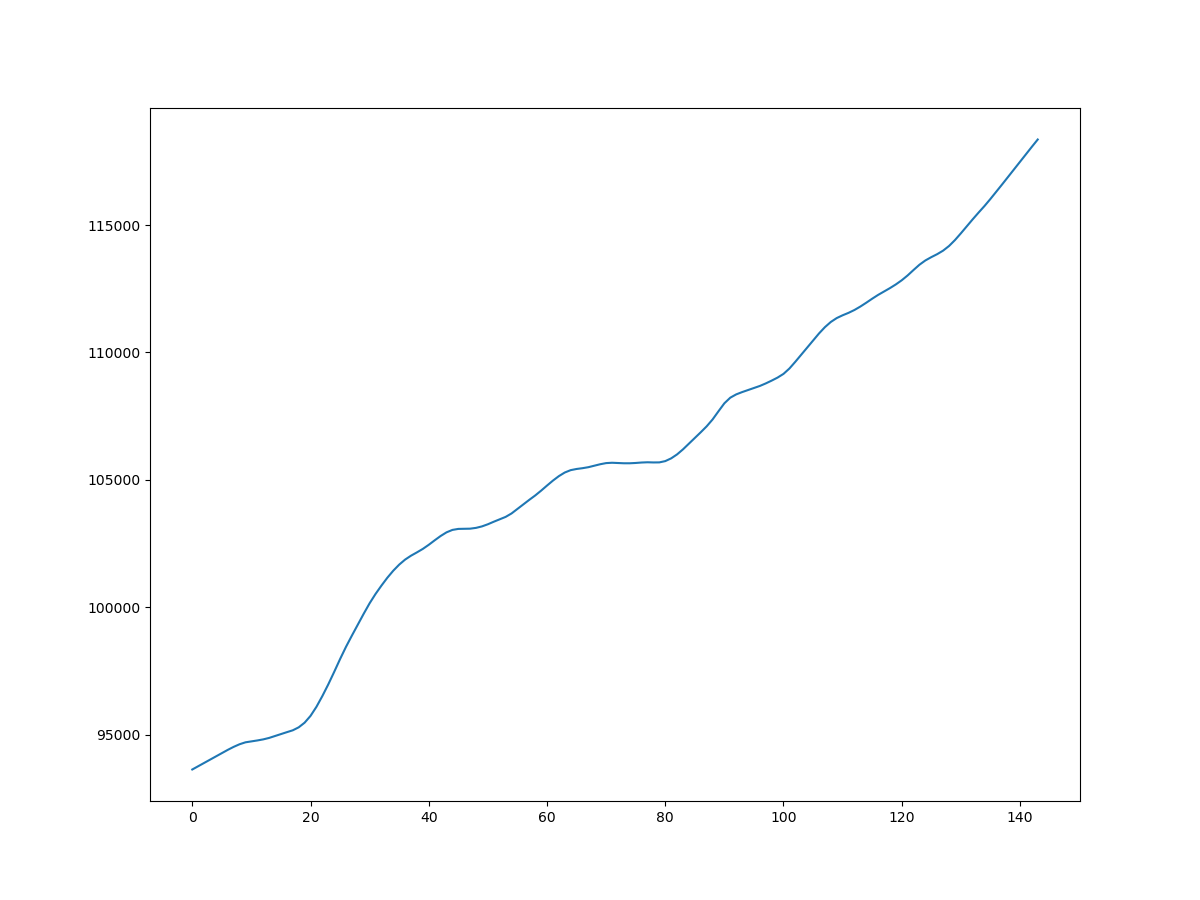 |
 |
そして、csvファイル出力は以下のようにやります。
import csv
with open('sample_pl2.csv', 'w') as f:
writer = csv.writer(f, delimiter='\n')
writer.writerow(pl2)
まとめ
・Rとpythonでdecompose()のやり方を並べてみた
・それぞれのコードは結果は少し異なるがほぼ同等のことが出来て、ノイズやトレンドが乗った周期的な変動を純粋な周期的な変動として取り出すことが出来た
・各要素分解された成分をcsvデータに書き出すことが出来、二次利用出来る
・実は今回は死亡数の経年変化を例として3月までの速報値を使ったが、その範囲では2011年のような異常値は見えていない(むしろ減少傾向)
・次に、周期的な変動要素を音に変換し聞いてみることとする
・非周期な変動要素についても(検定はともかく)やってみる