前回の記事でグラフは相関が見えていることを示したが、今回は全てのデータを使って、本格的にクラスタ分類し、どの騎手がという分析をする。
ただし、重要な知見として、以下の事項は教訓として意識する必要がありそうです。
「最も重要な点は,クラスタリングは探索的 (exploratory) なデータ解析手法であって,分割は必ず何らかの主観や視点に基づいているということです.よって,クラスタリングした結果は,データの要約などの知見を得るために用い,客観的な証拠として用いてはなりません.」参考②から引用
また、今回の記事は、ほぼ参考①のコードと技術を使っています。
【参考】
・①k-meansの最適なクラスター数を調べる方法
・②クラスタリング (クラスター分析)
・③クラスタ数を自動推定するX-means法を調べてみた
やったこと
・データの事前処理をする
・競馬騎手データの全データを使う⇒相関が見える
・1-20クラスタまで計算してdistortionをプロットする⇒最適クラスタ数を推定できる?
・シルエット係数を計算する⇒最適クラスタ数を推定できる?
・全データによるクラスタリングとPCA分析後の(第一成分、第二成分)のクラスタリング結果⇒多変量解析から次元圧縮
・データの事前処理をする
今回は、事前処理として偏差値に換算してある意味平等に扱うこととした。
元データは以下のリンク先のとおりで大きいものは獲得賞金の454469000
から、小さいものは勝率などの0.211まで幅が広く、どうみても民主的にフィッティングされるとは思えなかったからである。
【参考】
・・2019年度 リーディングジョッキー (全国)@騎手・調教師データのリーディングよりデータ取得
今回は、エクセル上で平均と標準偏差を求めて、偏差値を計算しました。
・競馬騎手データの全データを使う⇒相関が見える
import pandas as pd
import matplotlib.pyplot as plt
from pandas.tools import plotting
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
import numpy as np
df = pd.read_csv("keiba_std2.csv", sep=',', na_values=".")
df.head() #データの確認
df.iloc[:, 1:].head() #解析に使うデータは2列目以降
print(df.iloc[:, 1:])
plotting.scatter_matrix(df[df.columns[1:]], figsize=(6,6), alpha=0.8, diagonal='kde') #全体像を眺める
plt.savefig('k-means/keiba_std2_scatter_plot4.jpg')
plt.pause(1)
plt.close()
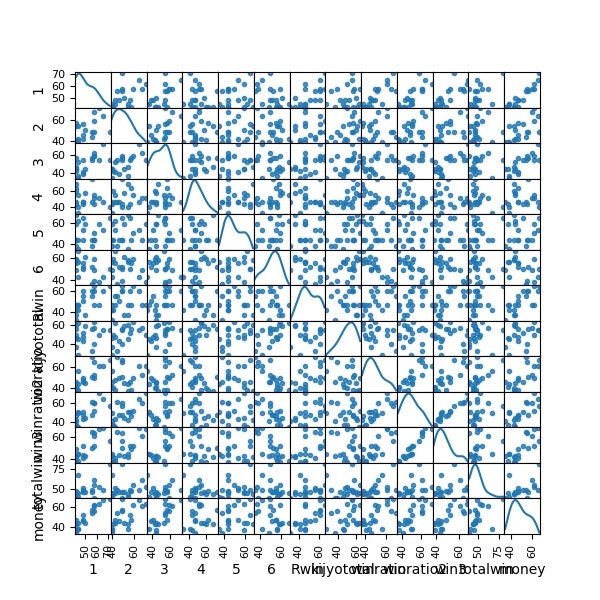
コード的にはクラスタリング後colors確定後に描画しているが、データ間の相関は以下のとおり
fig, axes = plt.subplots(nrows=13, ncols=13, figsize=(18, 18),sharex=False,sharey=False)
for i in range(1,14):
for j in range(1,14):
ax = axes[i-1,j-1]
x_data=df[df.columns[i]]
y_data=df[df.columns[j]]
#print(x_data)
ax.scatter(x_data,y_data,c=colors)
cor=np.corrcoef(x_data,y_data)[0, 1]
ax.set_title("{:.3f}".format(cor))
fig.savefig('k-means/pandas_std2_iris_line_axes'+str(s)+'.png')
・1-20クラスタまで計算してdistortionをプロットする⇒最適クラスタ数を推定できる?
distortions = []
distortions1 = []
for i in range(1,21): # 1~20クラスタまで一気に計算
km = KMeans(n_clusters=i,
init='k-means++', # k-means++法によりクラスタ中心を選択
n_init=10,
max_iter=300,
random_state=0)
km.fit(df.iloc[:, 1:]) # クラスタリングの計算を実行
distortions.append(km.inertia_) # km.fitするとkm.inertia_が得られる
UF = km.inertia_ + i*np.log(20)*5e2 # km.inertia_ + kln(size)
distortions1.append(UF)
fig=plt.figure(figsize=(12, 10))
ax1 = fig.add_subplot(311)
ax2 = fig.add_subplot(312)
ax3 = fig.add_subplot(313)
ax1.plot(range(1,21),distortions,marker='o')
ax1.set_xlabel('Number of clusters')
ax1.set_ylabel('Distortion')
# ax1.yscale('log')
ax2.plot(range(1,21),distortions,marker='o')
ax2.set_xlabel('Number of clusters')
ax2.set_ylabel('Distortion')
ax2.set_yscale('log')
ax3.plot(range(1,21),distortions1,marker='o')
ax3.set_xlabel('Number of clusters')
ax3.set_ylabel('Distortion+klog')
ax3.set_yscale('log')
plt.pause(1)
plt.savefig('k-means/keiba_std2_Distortion.jpg')
plt.close()
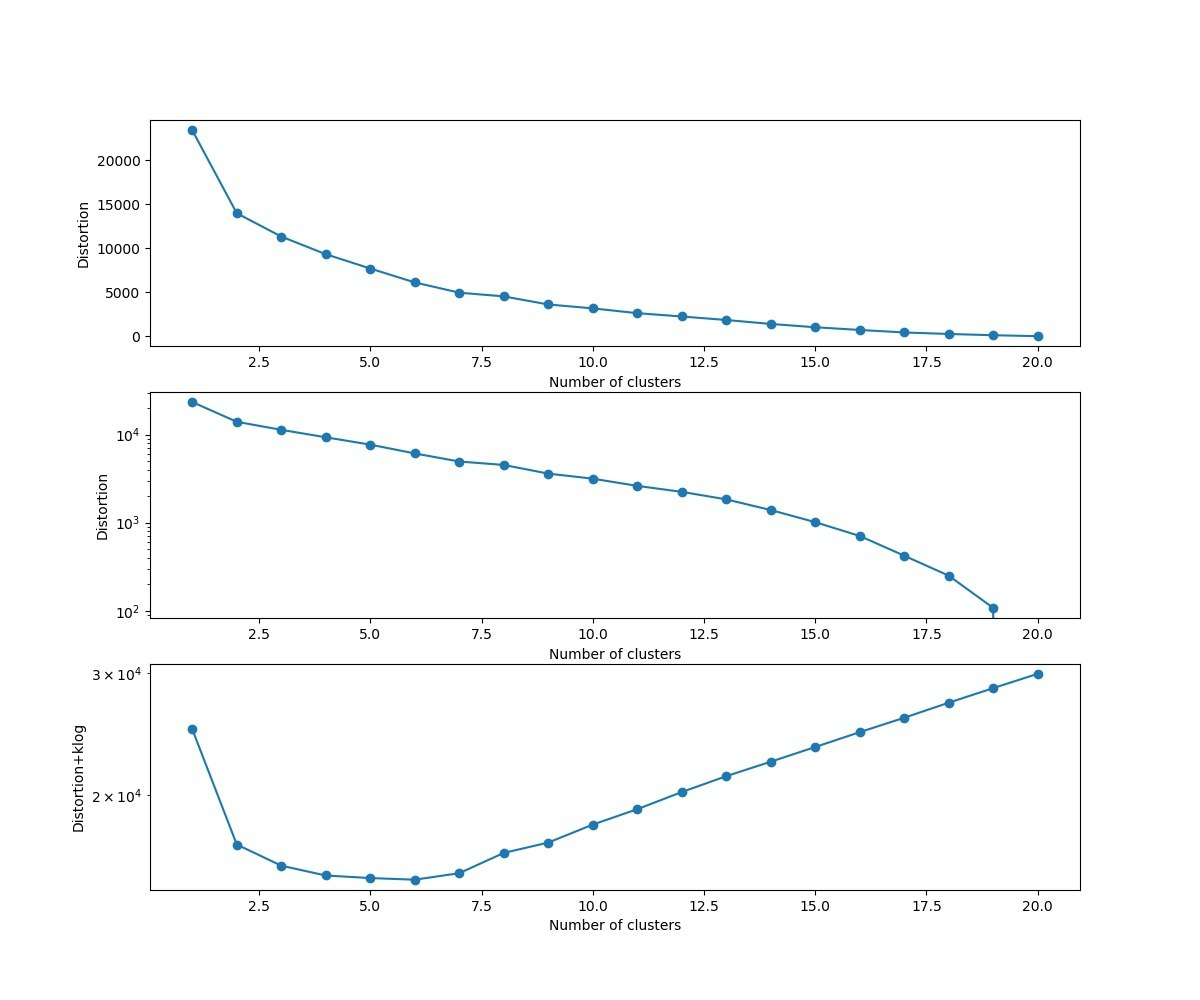
二番目の図は、縦軸を対数目盛にしました。
本当に表現力が劇的に変化しているのであれば、対数グラフで変曲点が見えると考えましたが、。。もともと通常の図でどこでクロスオーバーが発生しているかを見極めるのは難しいところです。ということで、三番目の図も書いてみました。
これは、参考③のBIC的考え方のモデルの説明変数は多くなるのを抑制するという考え方から引いています(厳密性はありません)。
※これは適当に入れただけですが、思考実験的にはこういうクロスオーバーが発生することを期待します
※「クラスター数は客観的な証拠とならない」という前提なのでだいたいの妥当性があればよいということです
・シルエット係数を計算する⇒最適クラスタ数を推定できる?
from sklearn.metrics import silhouette_samples
from matplotlib import cm
cluster_labels = np.unique(y_km) # y_kmの要素の中で重複を無くす s=6 ⇒ [0 1 2 3 4 5]
n_clusters=cluster_labels.shape[0] # 配列の長さを返す。つまりここでは n_clustersで指定したsとなる
# シルエット係数を計算
silhouette_vals = silhouette_samples(df.iloc[:, 1:],y_km,metric='euclidean') # サンプルデータ, クラスター番号、ユークリッド距離でシルエット係数計算
y_ax_lower, y_ax_upper= 0,0
yticks = []
for i,c in enumerate(cluster_labels):
c_silhouette_vals = silhouette_vals[y_km==c]
c_silhouette_vals.sort()
y_ax_upper += len(c_silhouette_vals)
color = cm.jet(float(i)/n_clusters)
plt.barh(range(y_ax_lower,y_ax_upper),
c_silhouette_vals,
height=1.0,
edgecolor='none',
color=color)
yticks.append((y_ax_lower+y_ax_upper)/2)
y_ax_lower += len(c_silhouette_vals)
silhouette_avg = np.mean(silhouette_vals)
plt.axvline(silhouette_avg,color="red",linestyle="--")plt.yticks(yticks,cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('silhouette coefficient')
plt.savefig('k-means/keiba_std2_silhouette_avg'+str(s)+'.jpg')
plt.pause(1)
plt.close()
以下を見ると、現実のデータのクラスタリングは難しそう。。。
※一応、2クラスか3クラスあたりが妥当なのかな。。。
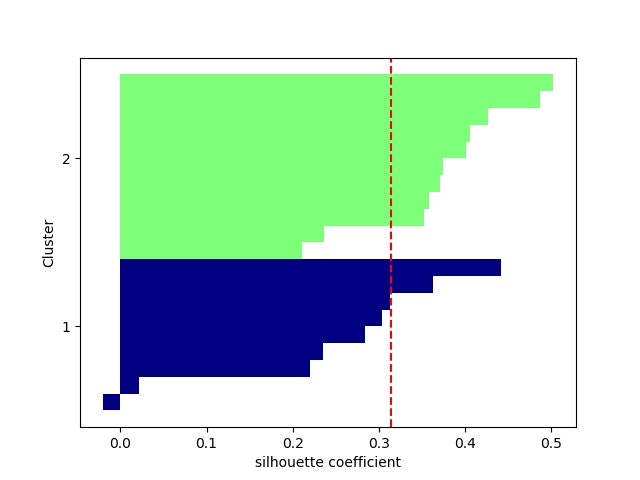
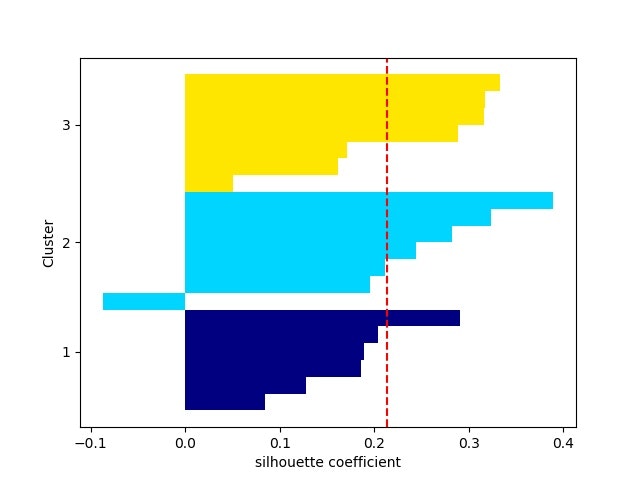
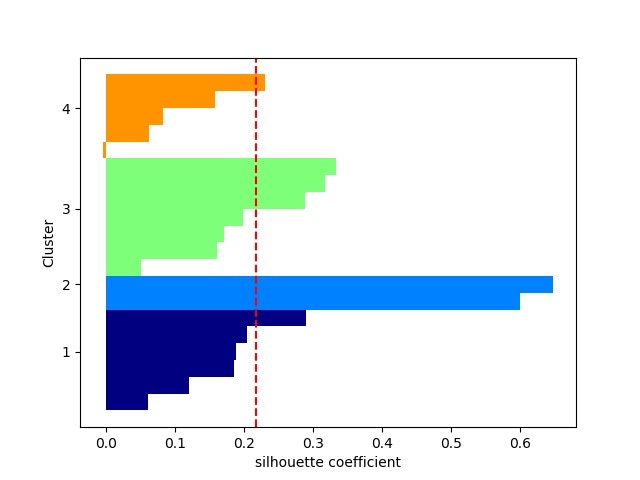
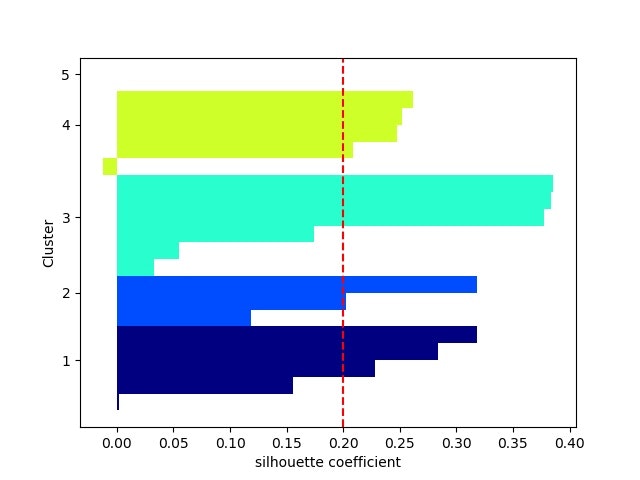
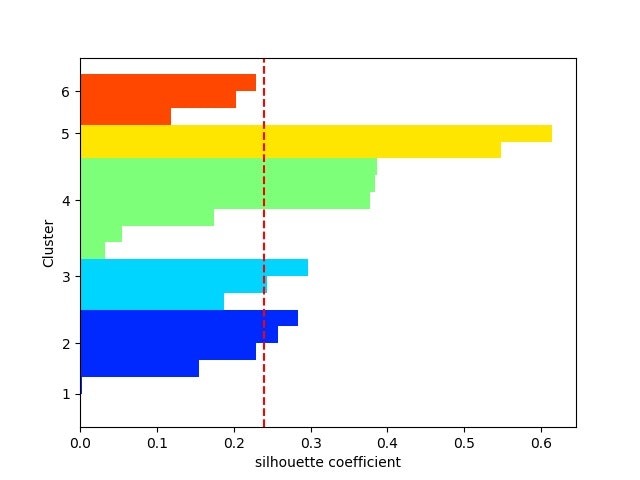
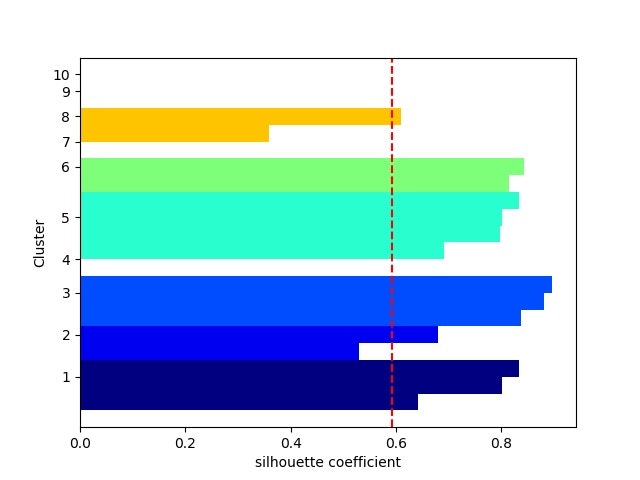
・PCA分析後の(第一主成分、第二主成分)面でのクラスタリング結果
多変量解析から次元圧縮してから、クラスタリングしてみました。
つまり、最大の関心はそのままクラスタリングしたものと変わるのかどうか。
まず、主成分分析を行い、x,y = feature[:, 0], feature[:, 1]により、第一、第二主成分をX=(x,y)に代入します。
# 主成分分析の実行
pca = PCA()
pca.fit(df.iloc[:, 1:])
PCA(copy=True, n_components=None, whiten=False)
# データを主成分空間に写像 = 次元圧縮
feature = pca.transform(df.iloc[:, 1:])
x,y = feature[:, 0], feature[:, 1]
# print(x,y)
X=np.c_[x,y]
上記のX=(x,y)を使って、この二次元面においてK-meansを使ってクラスタリングします。
kmeans_model = KMeans(n_clusters=s, random_state=10).fit(X)
print(kmeans_model.labels_)
print(kmeans_model.cluster_centers_[:,0], kmeans_model.cluster_centers_[:,1])
colors = [color_codes[x] for x in kmeans_model.labels_]
# 第一主成分と第二主成分でプロットする
plt.figure(figsize=(6, 6))
for kx, ky, name in zip(x, y, df.iloc[:, 0]):
plt.text(kx, ky, name, alpha=0.8, size=10)
plt.scatter(x, y, alpha=0.8, color=colors)
plt.scatter(kmeans_model.cluster_centers_[:,0], kmeans_model.cluster_centers_[:,1], c = "b", marker = "*", s = 50)
plt.title("Principal Component Analysis")
plt.xlabel("The first principal component score")
plt.ylabel("The second principal component score")
plt.savefig('k-means/keiba_std2_PCA12_plot'+str(s)+'.jpg')
plt.pause(1)
plt.close()
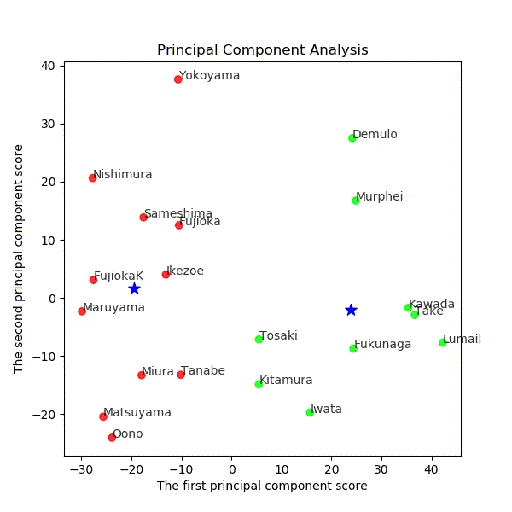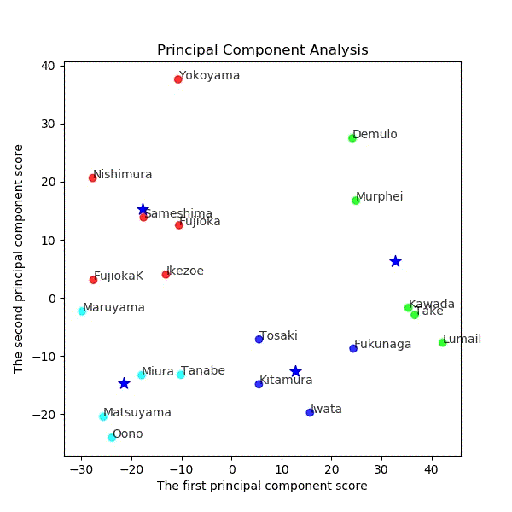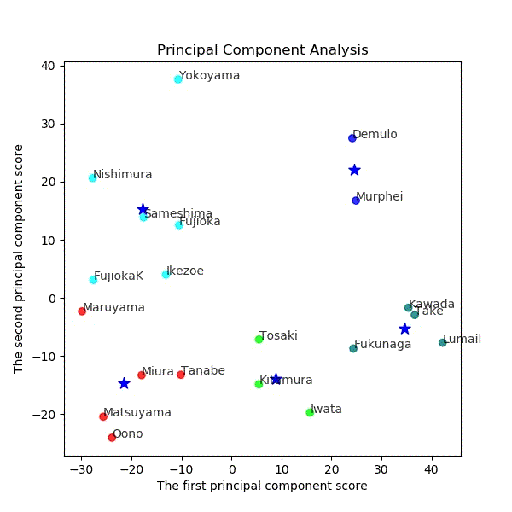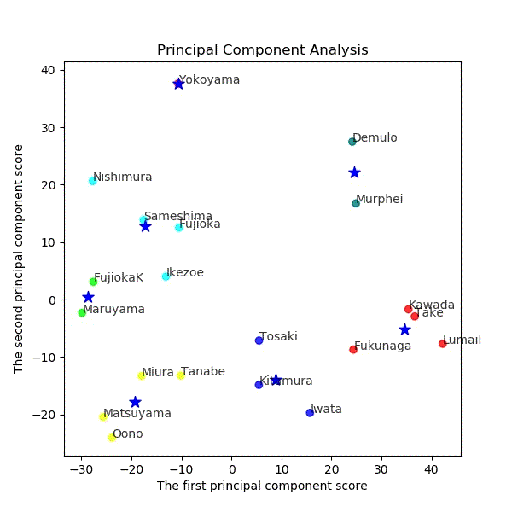
多変量でクラスタリング結果
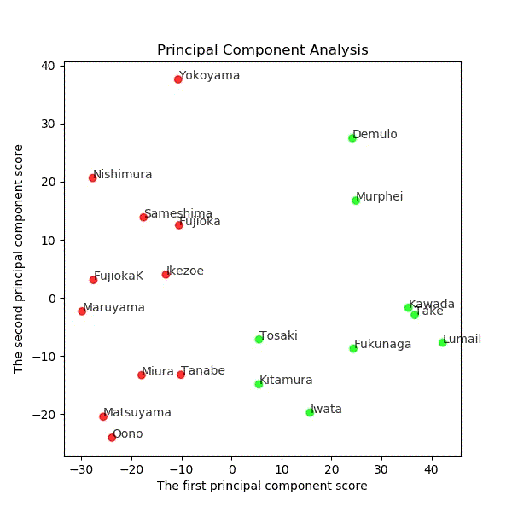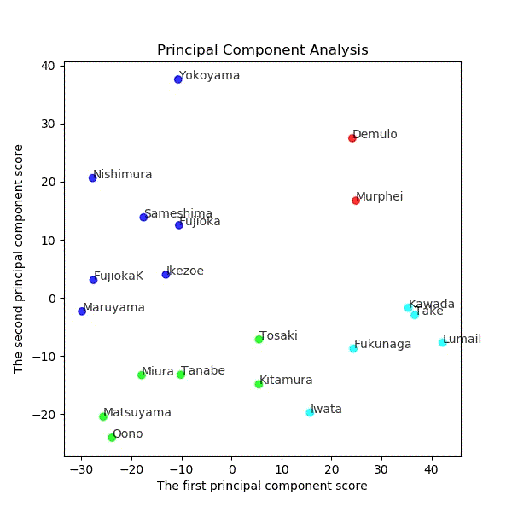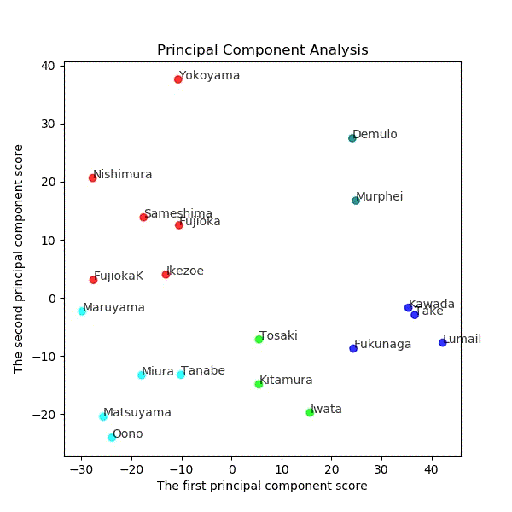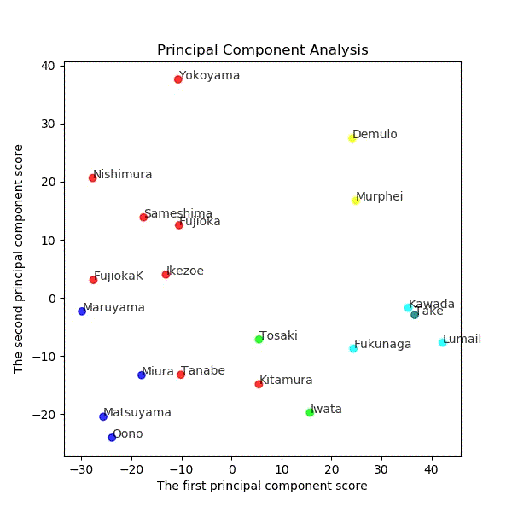
PCA後主成分-第二主成分面でクラスタリング結果
多変量とPCA後クラスタリングの結果比較
2クラス;同じ
[0 0 0 0 0 0 0 0 1 0 1 1 1 1 1 1 1 1 1 1]
[0 0 0 0 0 0 0 0 1 0 1 1 1 1 1 1 1 1 1 1]
3クラス;同じ
[0 0 0 0 2 0 2 0 2 2 1 1 1 2 1 2 2 1 1 1]
[1 1 1 1 0 1 0 1 0 0 2 2 2 0 2 0 0 2 2 2]
4クラス;異なる
[3 3 3 3 3 1 0 1 0 0 2 2 2 0 2 0 0 2 2 2]
[0 0 0 2 2 0 2 0 3 2 1 1 1 3 1 3 3 3 1 1]
5クラス;同じ
[2 2 2 2 0 4 0 4 3 0 1 1 1 3 1 3 3 3 1 1]
[4 4 4 4 0 2 0 2 1 0 3 3 3 1 3 1 1 1 3 3]
6クラス;異なる
[4 3 3 3 0 5 0 5 2 0 1 1 1 2 1 2 2 2 1 1]
[2 2 2 2 0 4 0 4 3 0 1 1 1 3 5 3 3 1 1 1]
7クラス;異なる
[4 3 3 3 0 5 6 5 2 0 1 1 1 2 1 6 2 2 1 1]
[1 1 1 1 2 4 2 4 5 2 3 3 3 5 6 5 5 0 3 0]
8クラス;異なる
[0 2 2 2 6 4 6 4 1 5 3 3 3 1 7 1 1 1 3 3]
[2 2 2 2 0 4 0 4 3 0 1 1 1 3 5 3 3 6 7 6]
9クラス;異なる
[4 5 5 5 3 0 3 0 2 8 1 1 7 2 6 2 2 2 7 1]
[2 2 2 2 0 4 0 4 8 0 1 1 1 3 5 8 3 6 7 6]
10クラス;異なる
[5 3 3 7 6 4 6 4 2 0 1 1 1 2 9 2 2 8 8 8]
[4 4 4 3 3 1 9 1 6 9 5 5 5 0 7 6 0 8 2 8]
まとめ
・k-meansで実データクラスタリングをやった
・クラス数の妥当性を見出すのは難しいことが分かる
・PCAで次元削減するのは有効なようだが、多変量で実施したものと一致するとは限らない
・単なる距離だけでのクラスタリングでは限界がある
・次回はちょっと理論的な話をしたいと思う
おまけ
name,1,2,3,4,5,6,Rwin,kijyototal,winratio,winratio2,win3,totalwin,money
Take,24,11,12,5,13,49,7,114,0.211,0.307,0.412,4042,454469000
Lumail,21,20,21,7,9,36,6,114,0.184,0.360,0.544,978,445864000
Kawada,19,24,12,9,11,28,3,103,0.184,0.417,0.534,1247,403594000
Fukunaga,17,22,16,9,6,48,3,118,0.144,0.331,0.466,2170,377694000
Iwata,17,17,14,10,8,65,7,131,0.130,0.260,0.366,1550,395310000
Murphei,17,11,14,6,6,30,6,84,0.202,0.333,0.500,25,327974000
Kitamura,16,11,13,17,6,53,6,116,0.138,0.233,0.345,664,340399000
Demulo,16,8,12,7,4,24,5,71,0.225,0.338,0.507,944,308588000
Miura,13,12,7,11,11,68,1,122,0.107,0.205,0.262,696,198769000
Tosaki,12,15,12,6,13,49,6,107,0.112,0.252,0.364,953,286602000
Fujioka,12,9,4,7,6,52,4,90,0.133,0.233,0.278,747,225422000
Ikezoe,12,7,5,7,9,59,5,99,0.121,0.192,0.242,1126,232521000
Sameshima,10,14,3,5,3,60,3,95,0.105,0.253,0.284,152,135654000
Matsuyama,10,7,11,10,12,79,3,129,0.078,0.132,0.217,556,195037000
Yokoyama,10,5,2,2,6,36,2,61,0.164,0.246,0.279,2742,131128000
Tanabe,9,16,13,13,6,58,3,115,0.078,0.217,0.330,806,226342000
Oono,9,14,8,15,14,64,1,124,0.073,0.185,0.250,504,185507000
Maruyama,9,6,6,12,6,65,2,104,0.087,0.144,0.202,454,188557000
Nishimura,9,5,7,7,4,47,0,79,0.114,0.177,0.266,22,89754000
FujiokaK,9,5,7,6,11,60,3,98,0.092,0.143,0.214,517,121869000
1 2 3 4 5 6 Rwin kijyototal winratio \
0 71.24 49.21 54.81 41.01 64.77 49.81 65.29 55.35 66.46
1 65.47 64.19 72.97 46.40 52.84 42.34 60.51 55.35 60.68
2 61.63 70.86 54.81 51.80 58.80 37.75 46.18 49.64 60.68
3 57.78 67.52 62.88 51.80 43.89 49.23 46.18 57.42 52.12
4 57.78 59.20 58.84 54.50 49.86 59.00 65.29 64.17 49.12
5 57.78 49.21 58.84 43.70 43.89 38.90 60.51 39.77 64.54
6 55.86 49.21 56.82 73.39 43.89 52.11 60.51 56.39 50.83
7 55.86 44.21 54.81 46.40 37.93 35.45 55.73 33.02 69.46
8 50.09 50.87 44.71 57.20 58.80 60.72 36.62 59.50 44.20
9 48.17 55.87 54.81 43.70 64.77 49.81 60.51 51.71 45.27
10 48.17 45.88 38.66 46.40 43.89 51.53 50.96 42.89 49.76
11 48.17 42.55 40.68 46.40 52.84 55.55 55.73 47.56 47.20
12 44.32 54.20 36.64 41.01 34.95 56.13 46.18 45.48 43.77
13 44.32 42.55 52.79 54.50 61.78 67.04 46.18 63.14 37.99
14 44.32 39.22 34.62 32.91 43.89 42.34 41.40 27.83 56.40
15 42.40 57.53 56.82 62.59 43.89 54.98 46.18 55.87 37.99
16 42.40 54.20 46.73 67.99 67.75 58.42 36.62 60.54 36.92
17 42.40 40.88 42.70 59.89 43.89 59.00 41.40 50.16 39.92
18 42.40 39.22 44.71 46.40 37.93 48.66 31.84 37.18 45.70
19 42.40 39.22 44.71 43.70 58.80 56.13 46.18 47.04 40.99
winratio2 win3 totalwin money
0 57.51 56.07 80.87 66.96
1 64.24 67.69 49.31 66.19
2 71.49 66.81 52.08 62.44
3 60.56 60.82 61.59 60.14
4 51.54 52.02 55.20 61.70
5 60.81 63.82 39.50 55.72
6 48.11 50.17 46.08 56.82
7 61.45 64.43 48.96 54.00
8 44.55 42.86 46.41 44.25
9 50.52 51.84 49.05 52.05
10 48.11 44.27 46.93 46.61
11 42.90 41.10 50.84 47.24
12 50.65 44.80 40.80 38.64
13 35.27 38.90 44.97 43.91
14 49.76 44.36 67.48 38.24
15 46.07 48.85 47.54 46.70
16 42.01 41.80 44.43 43.07
17 36.80 37.57 43.92 43.34
18 40.99 43.21 39.47 34.56
19 36.67 38.63 44.56 37.42