ついに出来たのかもしれない。。。ということでフォルマント合成ですが、リアルな音声の再現ができたようです。
本物はどっちだ？？
| 1 | 2 |
|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
やったこと
・本物の音声をよく見ると
・音声と似たフォルマントを作る
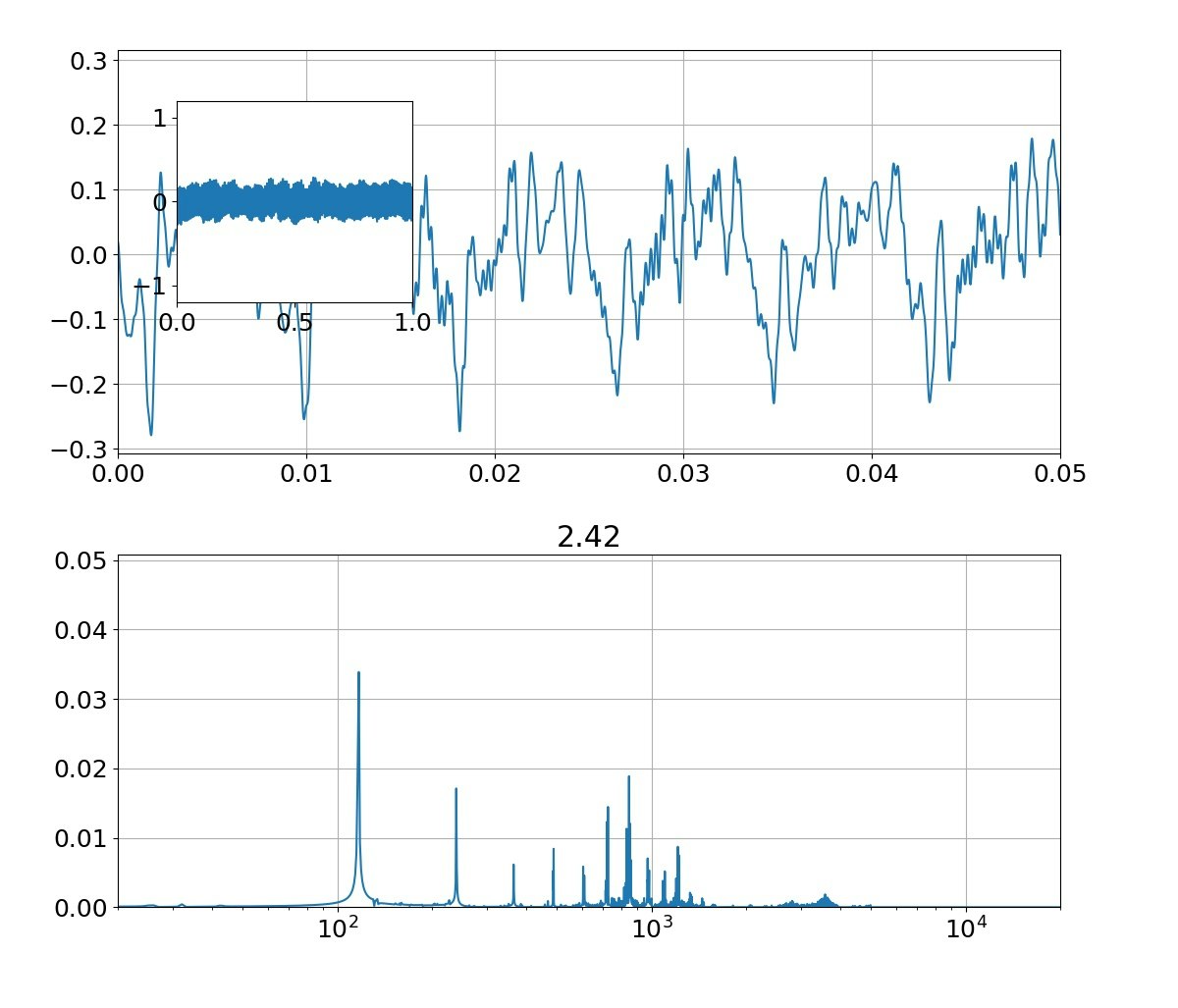
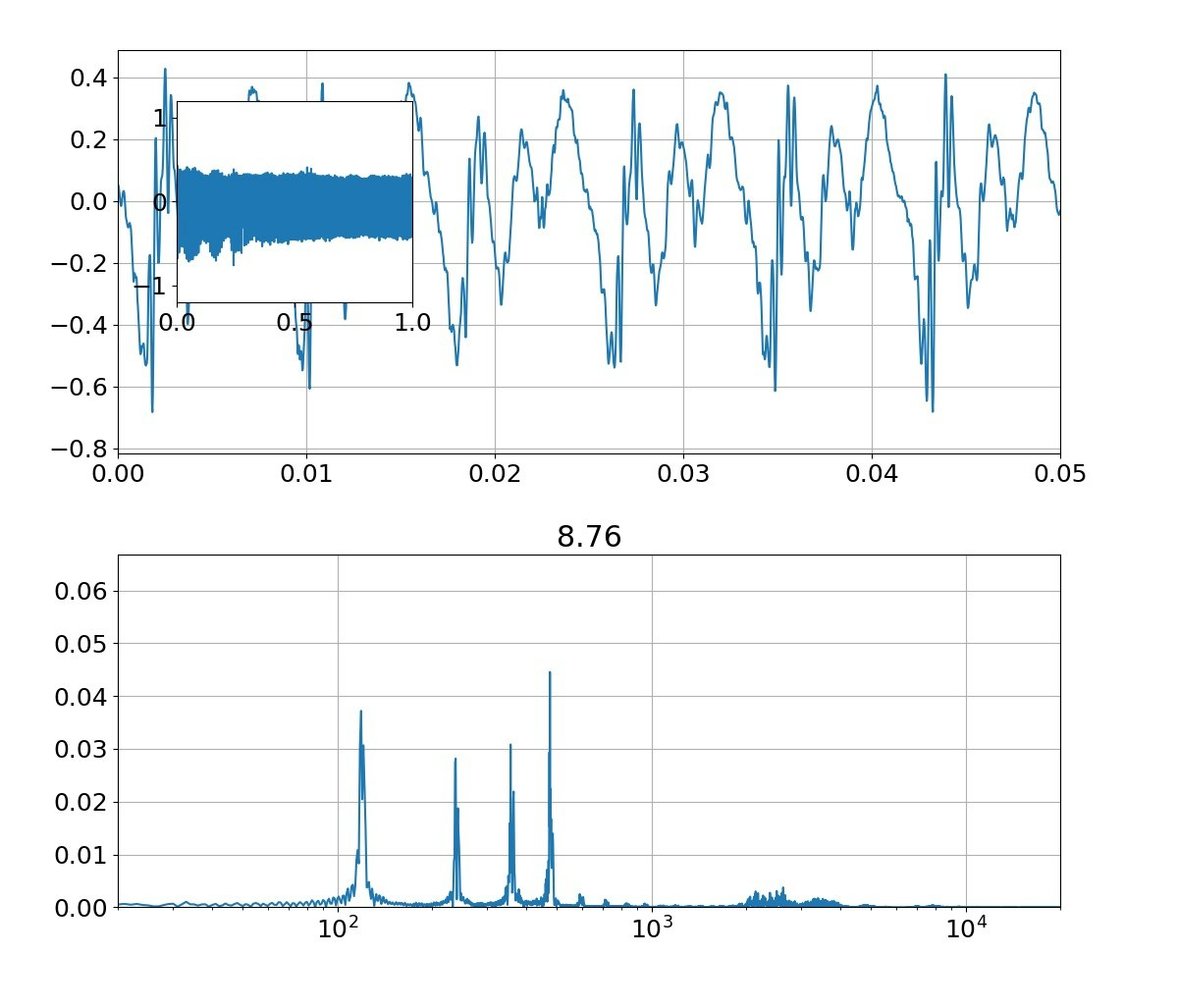
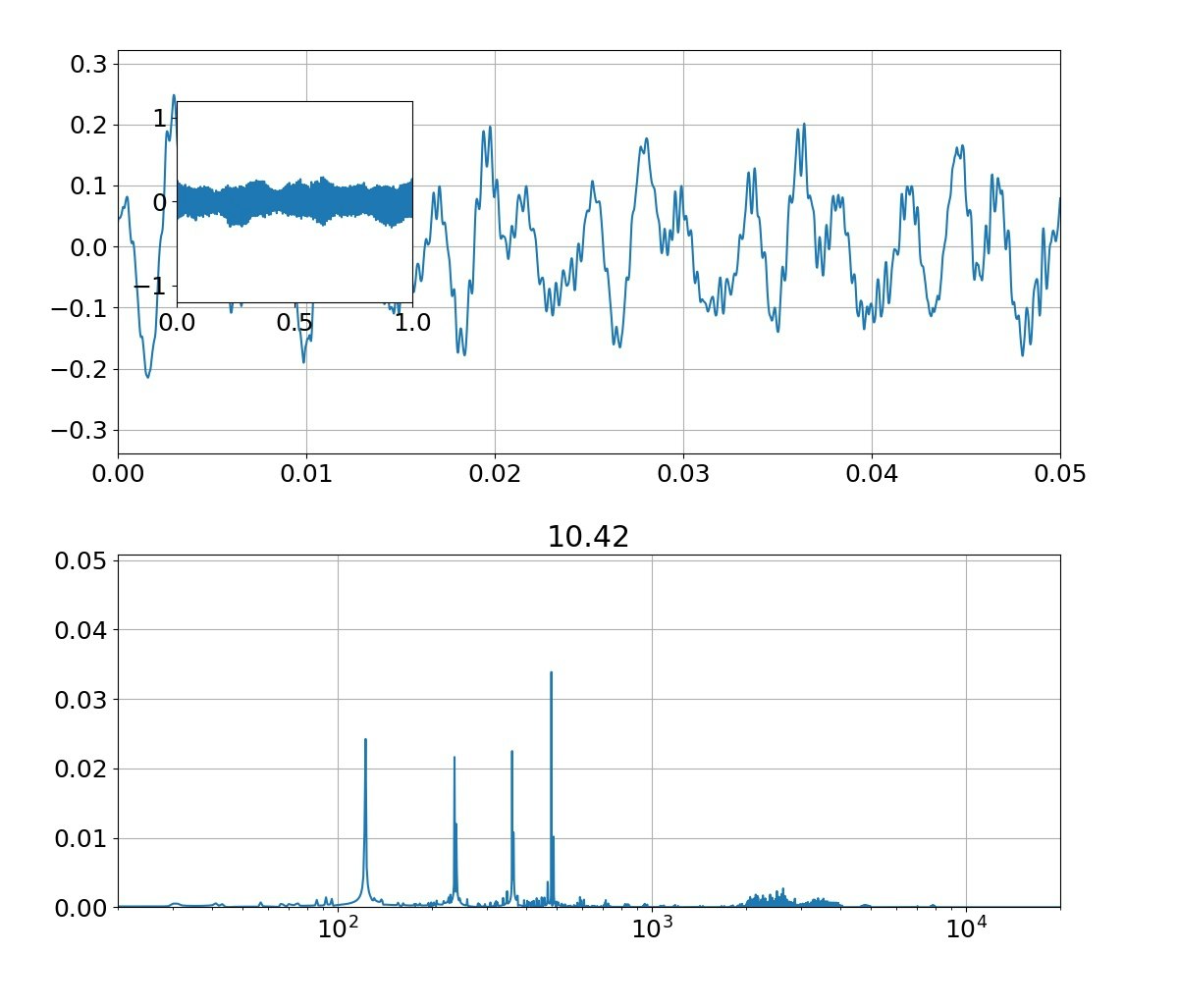
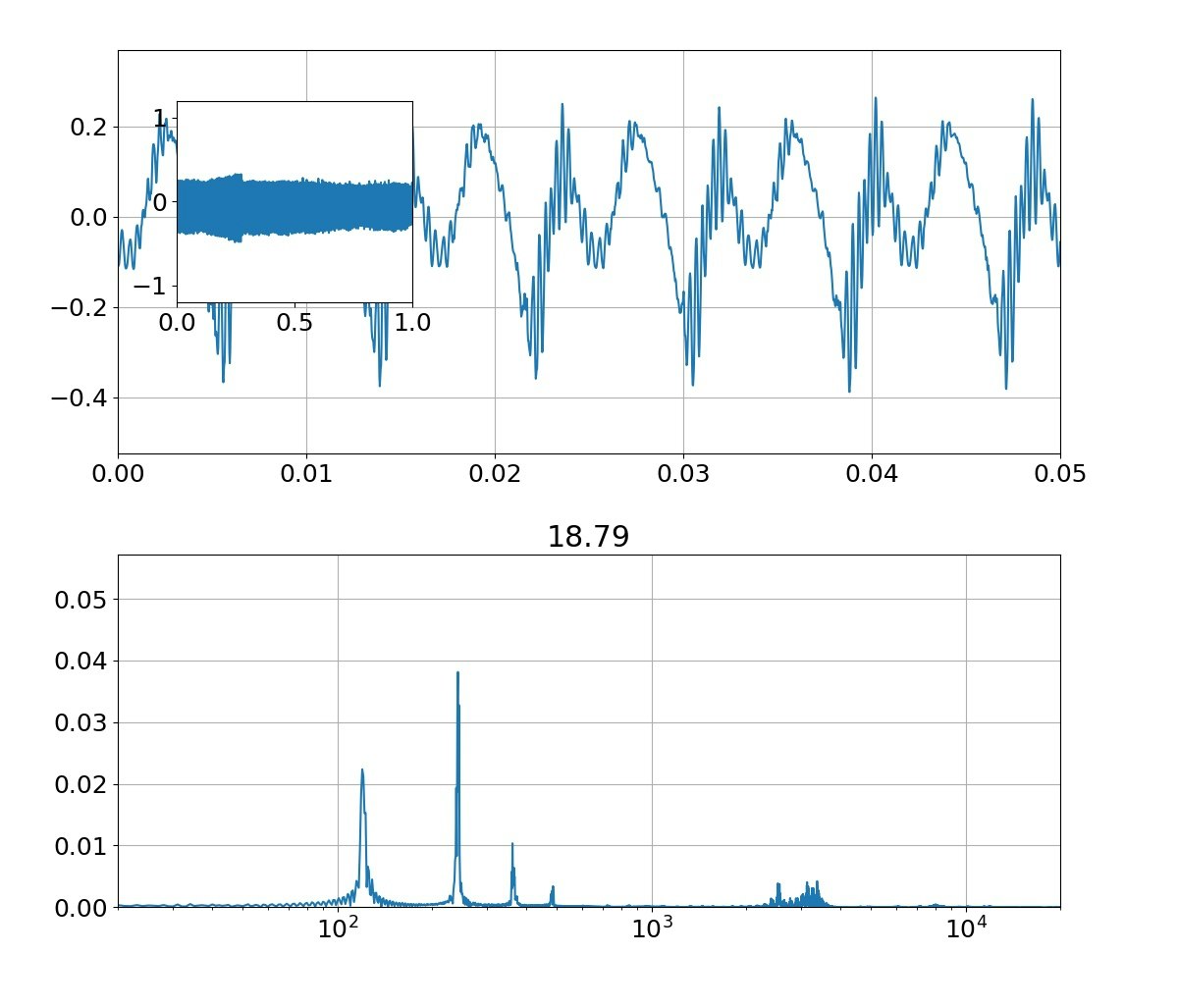
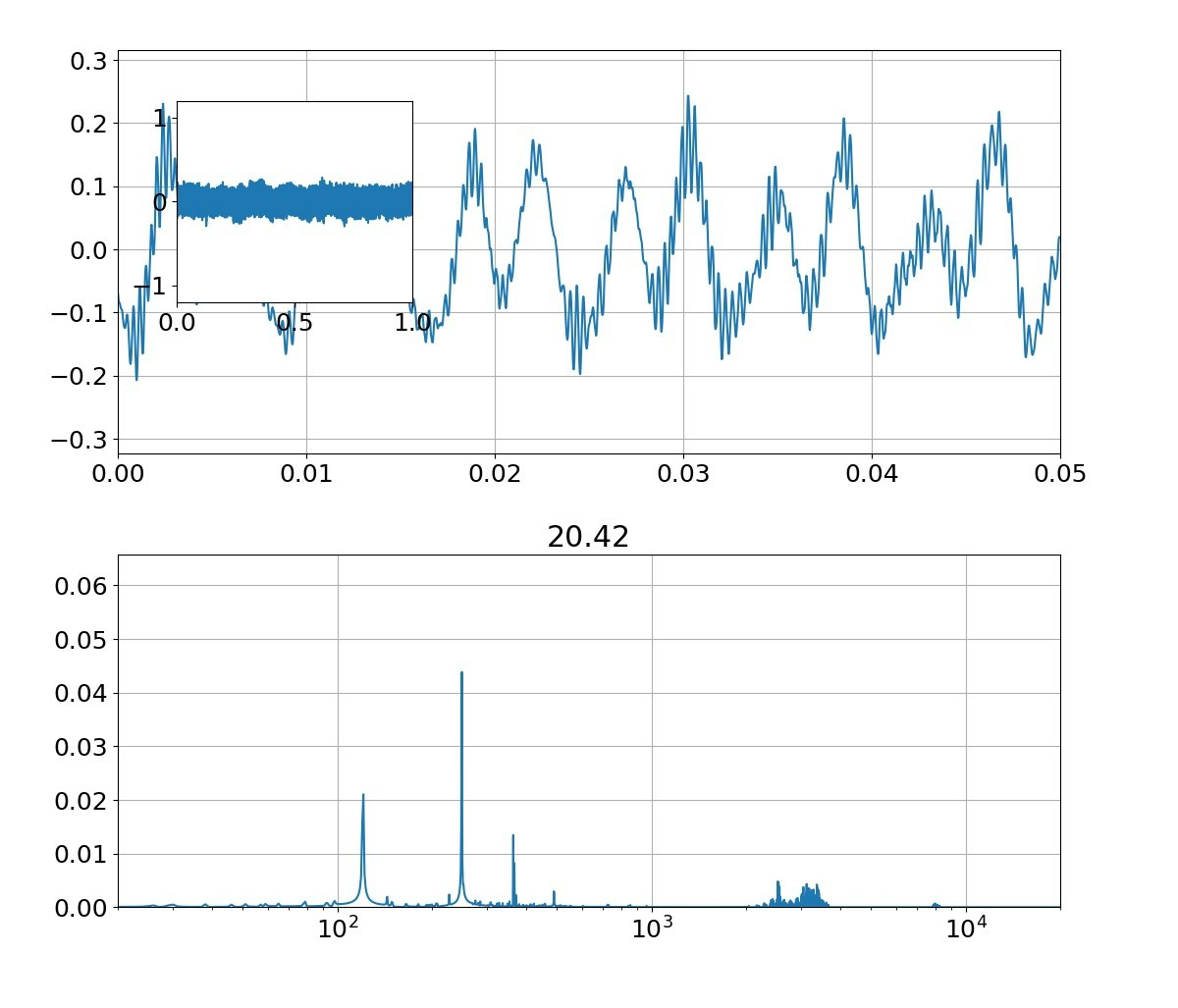
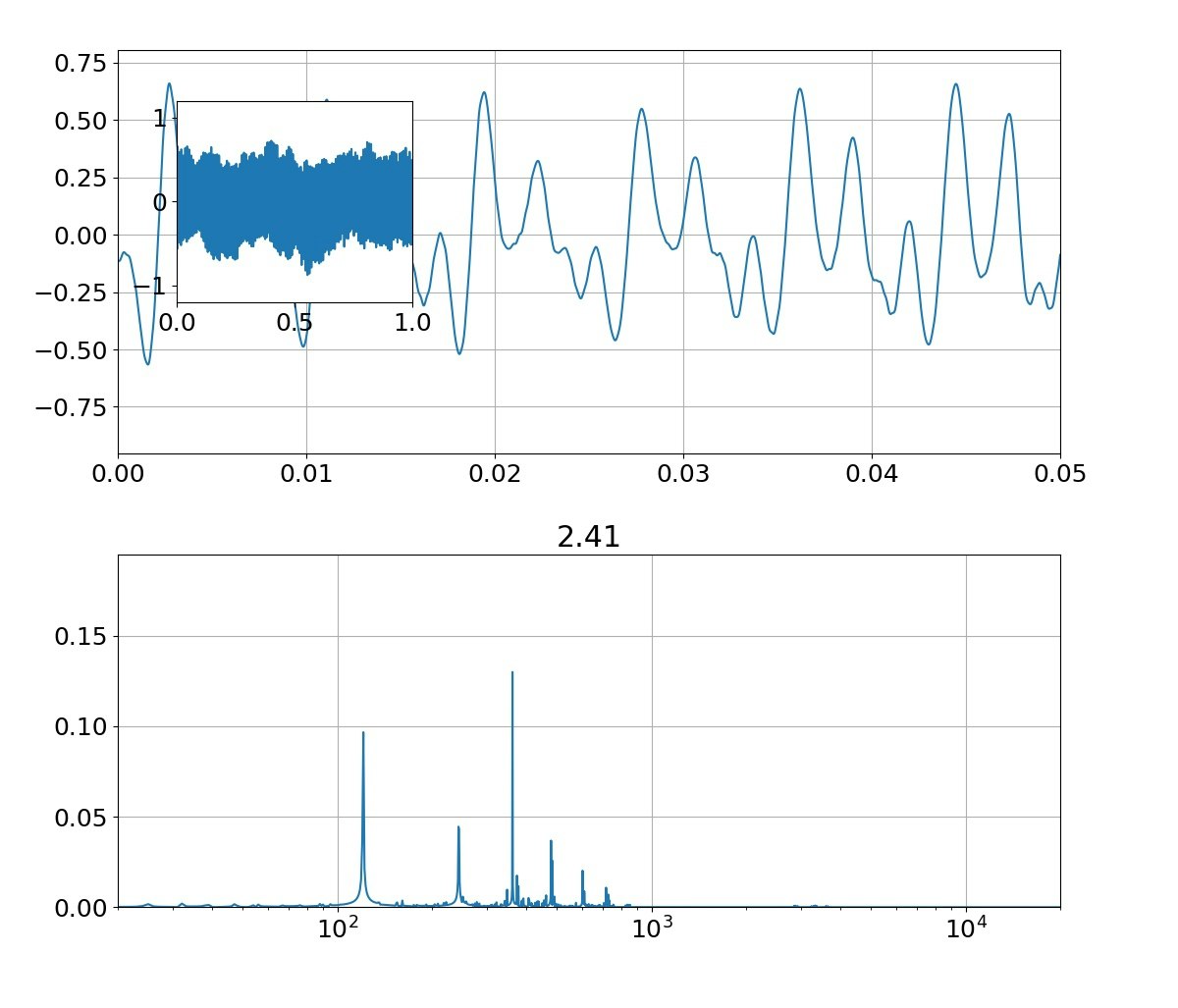
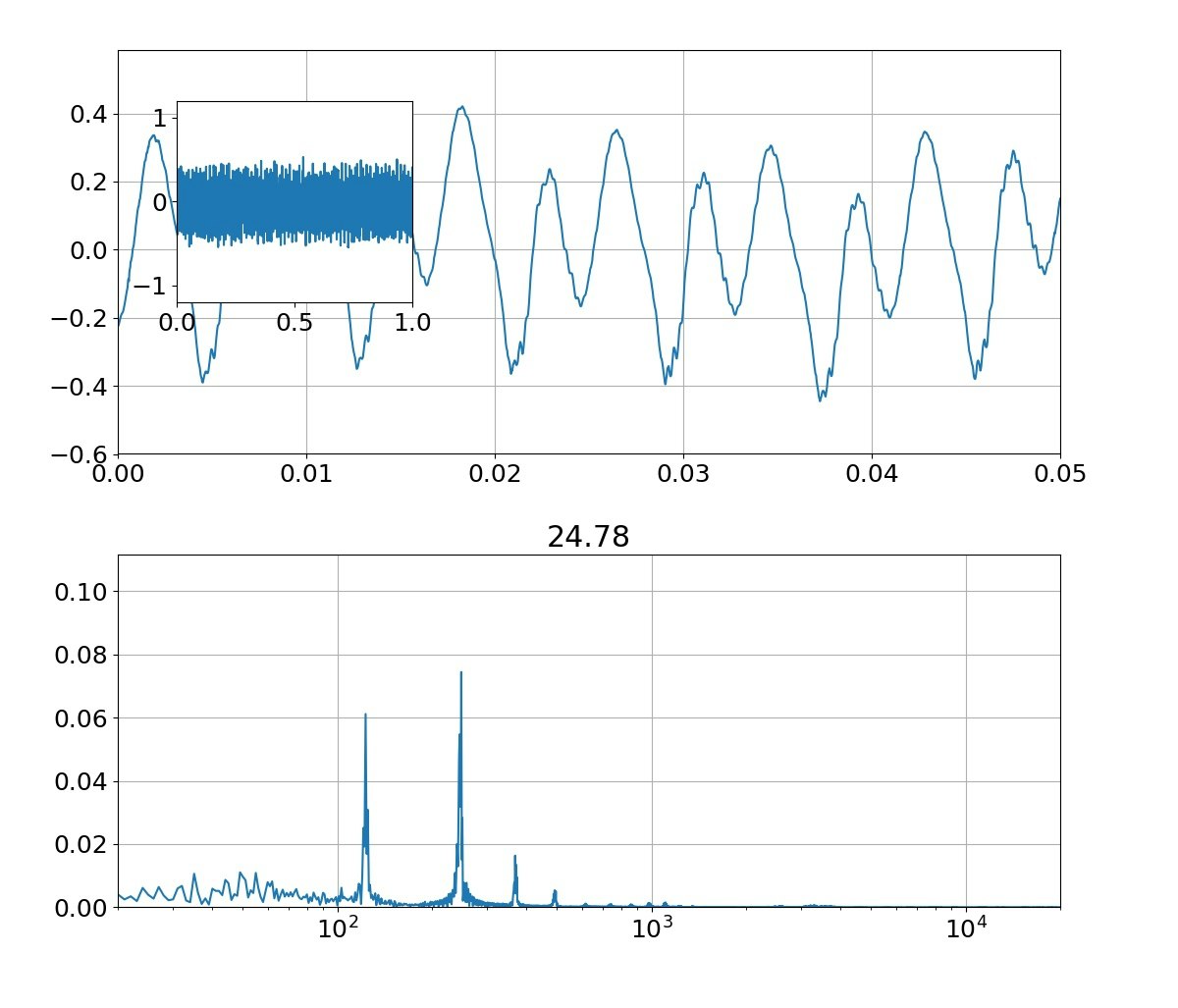
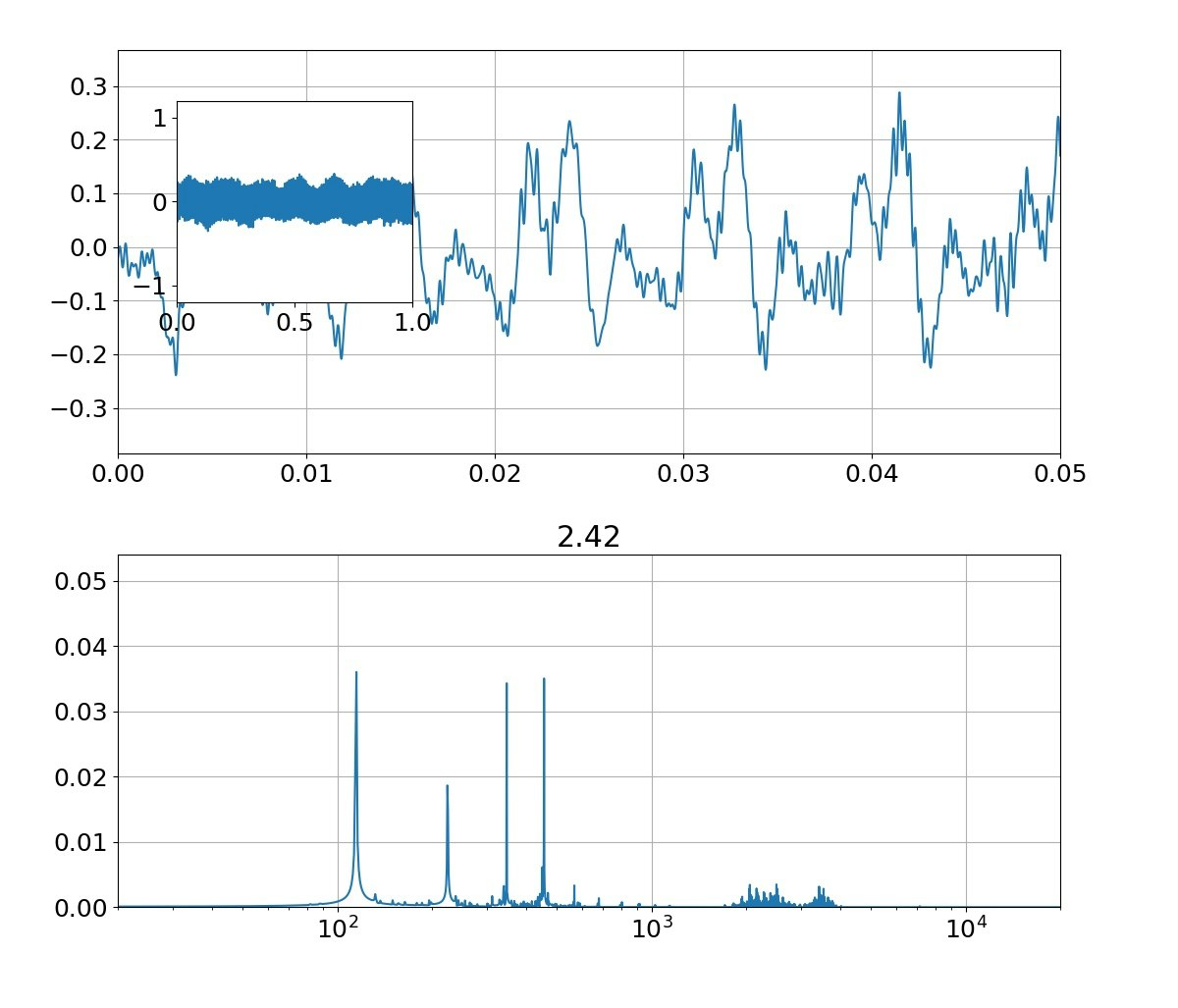
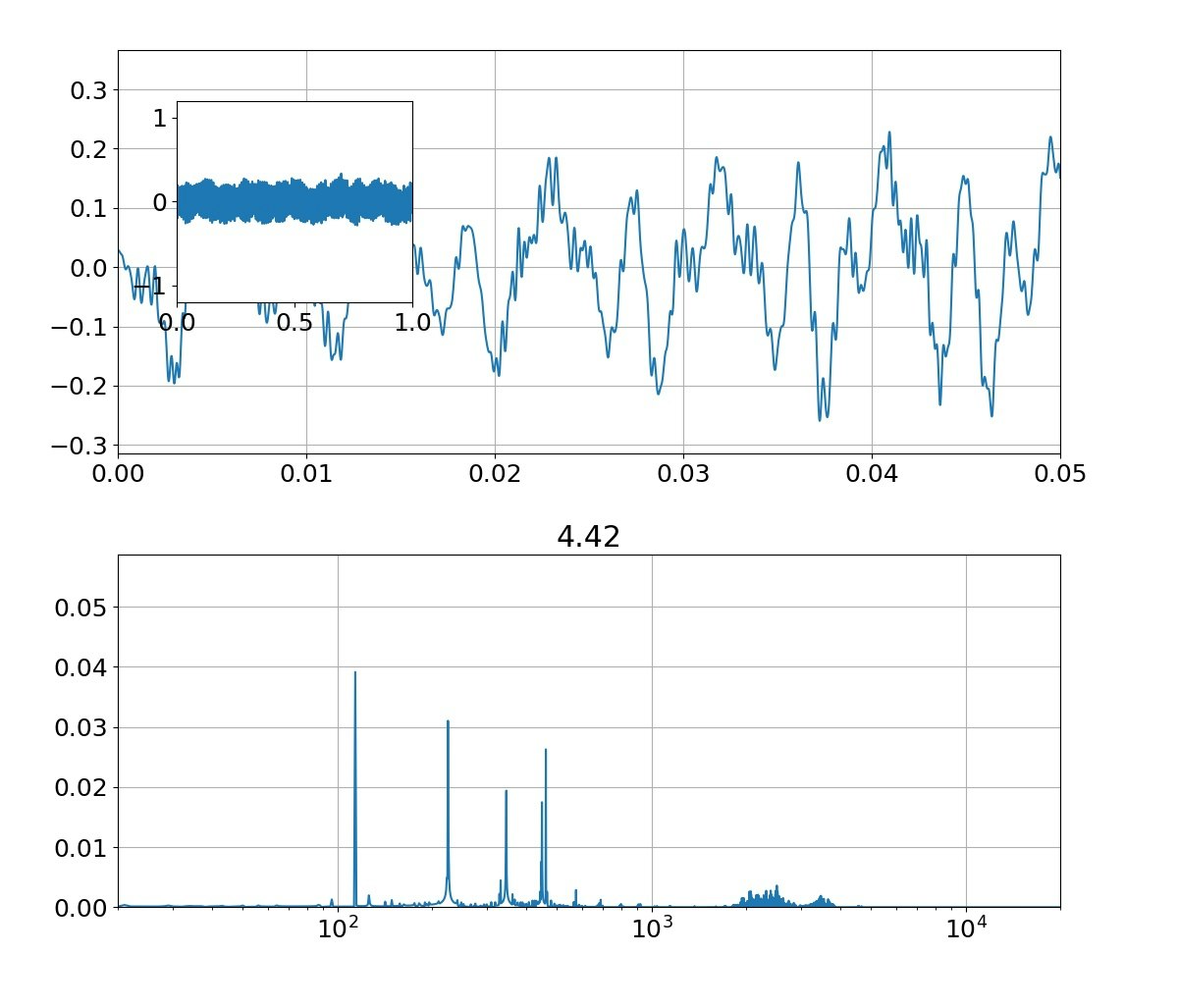
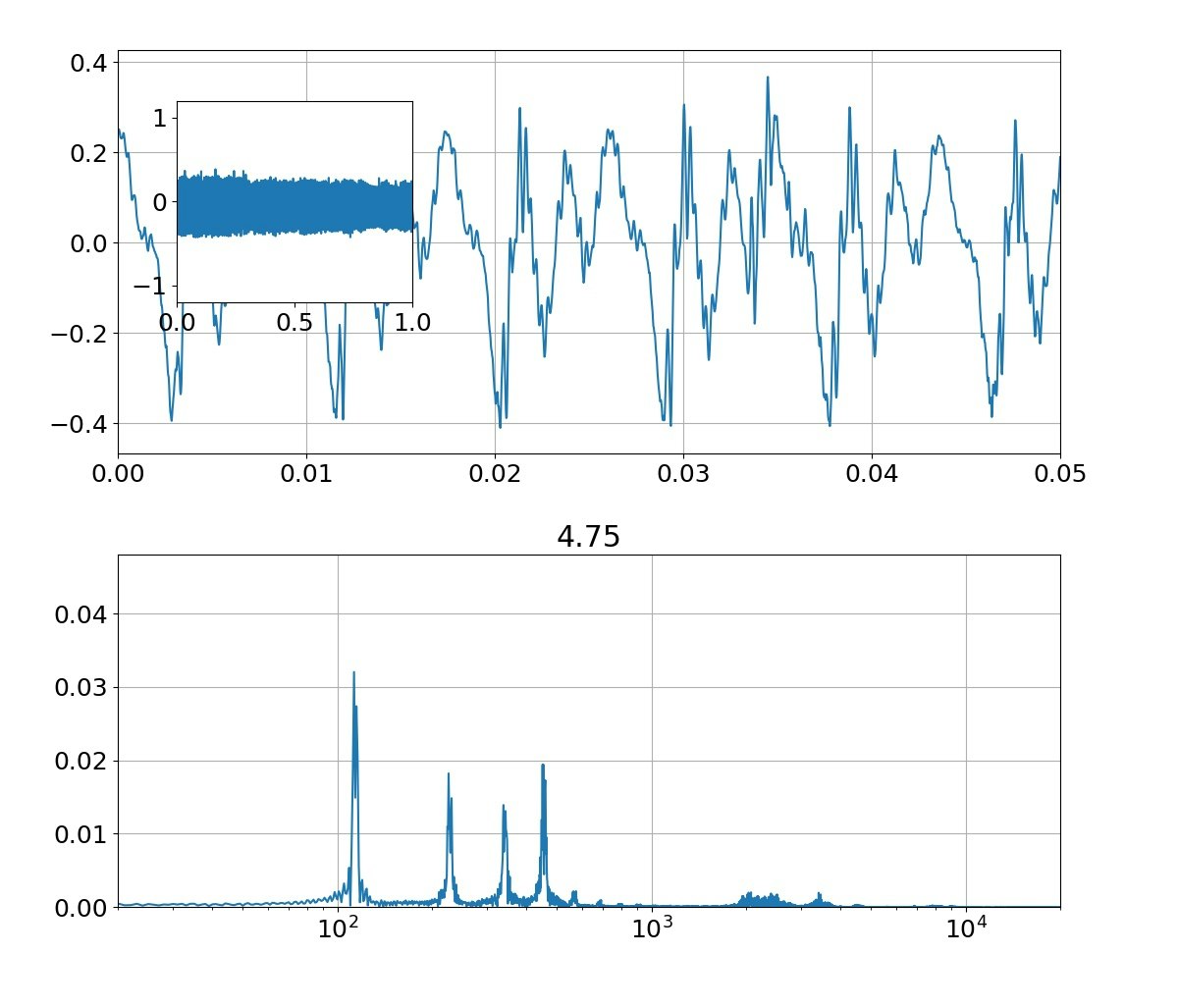
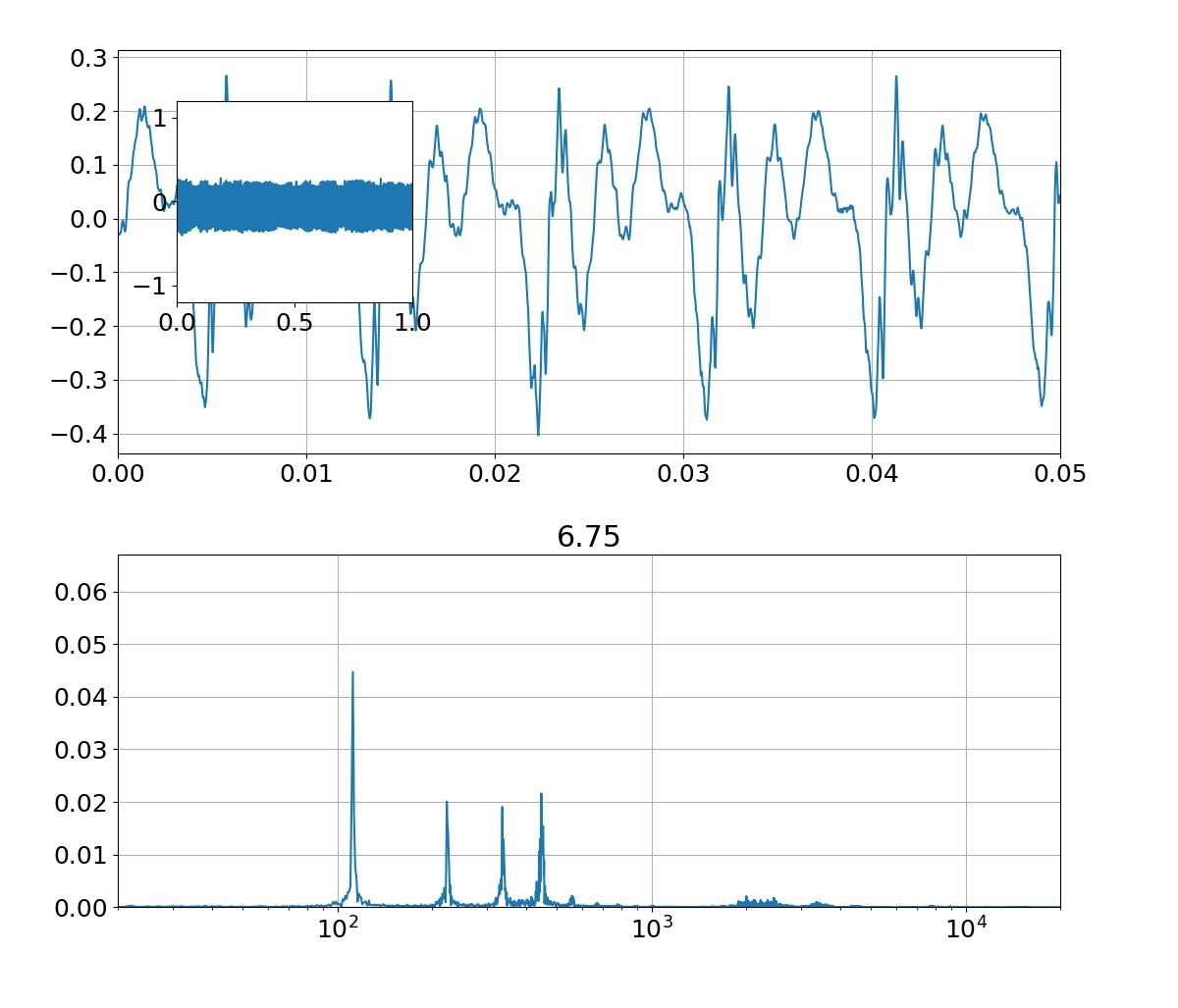
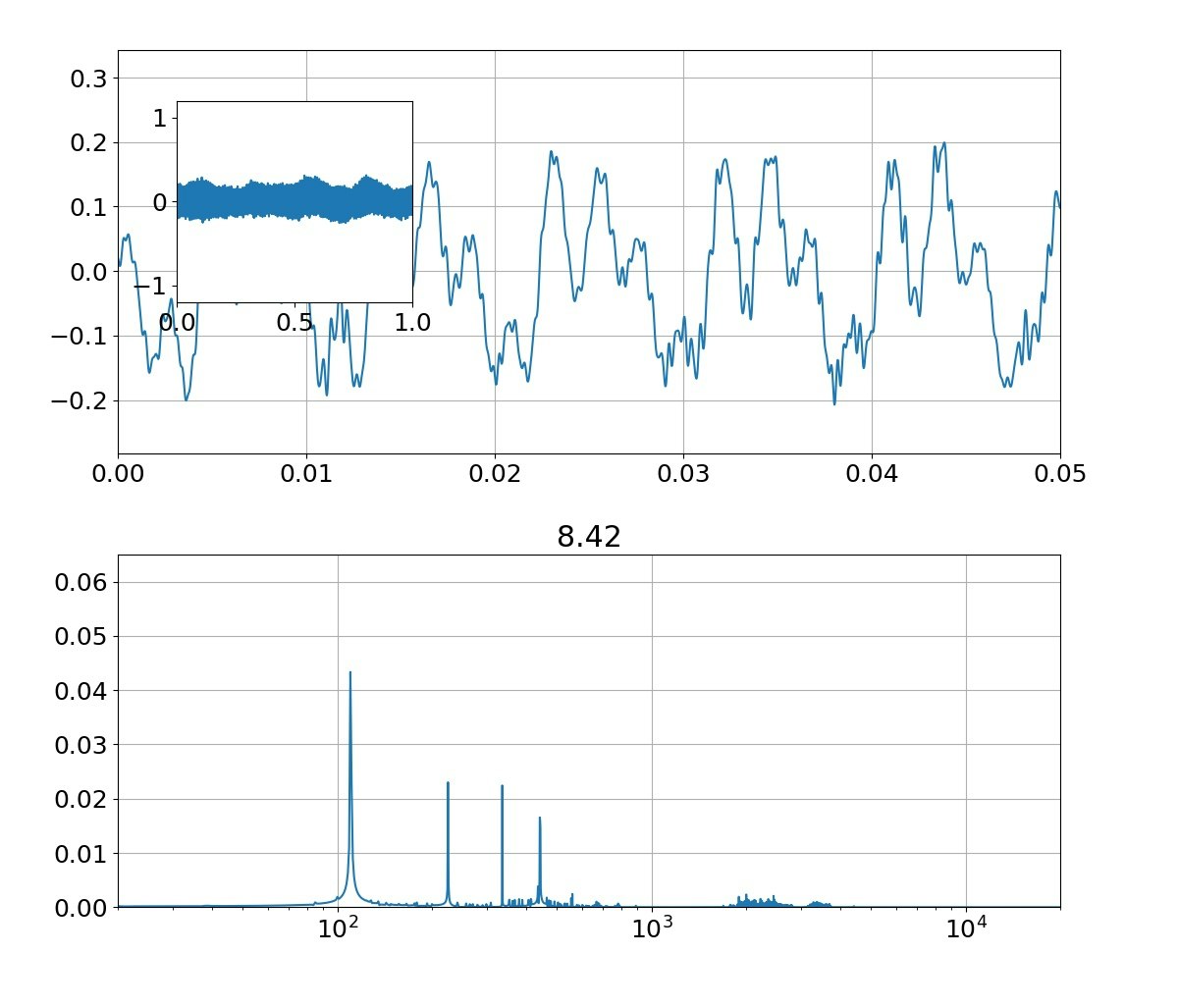
・リアル音声のFFTとフォルマント合成音声のFFT図
・本物の音声をよく見ると
本物がどっちかは別にして、上記のフォルマント（振幅の大きなピーク）を見ると、
①基準振動の整数倍のピーク以外に、小さな高周波ピークが集団で発生している
②ピークは裾が広がっている
という二つの特徴がある。
①については、先日の記事でorder=1や適当にピーク抽出の制約を工夫すれば行けるめどがあった。これだけでも一応音声っぽい音は発生できていたが、それだけでは、あの金属的な音になってしまっていた。
ということで、ここでは本物の音声を再現するために、この裾を本物っぽく作ることとした。
・音声と似たフォルマントを作る
普通こういう単一ピークに裾を作るには、サブピークを追加するのだが、このサブピークは綺麗な裾状になっている。つまり、ある連続的な周波数のピーク、すなわち一定の基準振動の周りに分布する一連のピークであると想像できる。すなわち一番簡単な解釈は適当に正規分布する振動数で発する音の重ね合わせで構成されていると考察するのが素直である。
参考から、正規分布する関数は以下のように作成できる。
【参考】
・Numpyによる乱数生成まとめ
R=[]
for i in range(10000):
r = 100+randn() # 標準正規分布で乱数を1万個生成
R.append(r)
plt.hist(R, bins=100) # 100本のヒストグラムを作成
plt.pause(1)
plt.savefig('./fft_sound/figure_histgram.jpg')
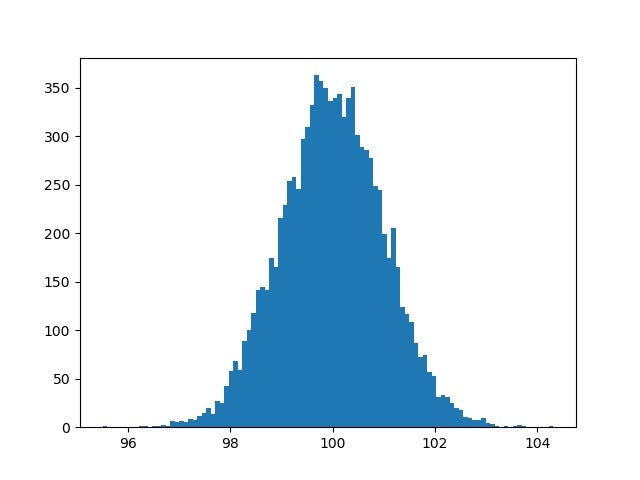
この乱数を使って、周波数が正規分布するサイン波は以下のように作成できる。
def sin_wav(A,f1,fr,sec):
point = np.arange(0,fr*sec)
f0=f1 #+2*randn()
sin_wav =0.01*A* (np.sin(2*np.pi*f0*point/fr))
return sin_wav,f0
fr=44100
sec=1
fn= fr*sec
t = np.linspace(0,sec, fn)
f0=400
sin_wave=0
f=[]
for i in range(0,1000,1):
f1=f0+2*randn()
sw,f2=sin_wav(A,f1,fr,sec)
sin_wave += sw
f.append(f2)
sin_wave = [int(x * 32767.0) for x in sin_wave]
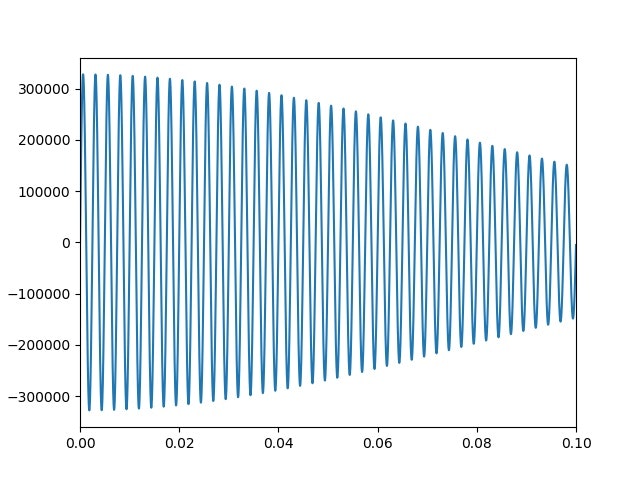
plt.plot(t,sin_wave)
plt.xlim(0,0.1*sec)
plt.savefig('./fft_sound/create_sin'+str(sec)+'.jpg')
plt.pause(1)
plt.close()
| 1 | 2 |
|---|---|
 |
 |
| そして、以下のコードでFFTする |
def FFT(sig,fn,fr):
freq =fft(sig,fn)
Pyy = np.sqrt(freq*freq.conj())/fn
f = np.arange(0,fr,fr/fn)
ld = signal.argrelmax(Pyy, order=3) #相対強度の最大な番号をorder=10で求める
ssk=0
fsk=[]
Psk=[]
maxPyy=max(np.abs(Pyy))
for i in range(len(ld[0])): #ピークの中で以下の条件に合うピークの周波数fと強度Pyyを求める
if np.abs(Pyy[ld[0][i]])>0.005*maxPyy and f[ld[0][i]]<20000 and f[ld[0][i]]>20:
fssk=f[ld[0][i]]
Pssk=np.abs(Pyy[ld[0][i]])
fsk.append(fssk)
Psk.append(Pssk)
ssk += 1
return freq,Pyy,fsk,Psk,f
start_time=time.time()
def draw_pic(freq,Pyy,fsk,Psk,f,sk,sig,sec):
matplotlib.rcParams.update({'font.size': 18, 'font.family': 'sans', 'text.usetex': False})
fig = plt.figure(figsize=(12,12)) #(width,height)
axes1 = fig.add_axes([0.1, 0.55, 0.8, 0.4]) # main axes
axes2 = fig.add_axes([0.15, 0.7, 0.2, 0.2]) # insert axes
axes3 = fig.add_axes([0.1, 0.1, 0.8, 0.35]) # main axes
axes1.plot(t, sig)
axes1.grid(True)
axes1.set_xlim([0, 0.05])
axes2.set_xlim(0,sec)
axes2.plot(t,sig)
Pyy_abs=np.abs(Pyy)
axes3.plot(f,Pyy_abs)
#axes3.axis([min(fsk)*0.9, max(fsk)*1.1, 0,max(Pyy_abs)*1.5]) #0.5, 2
axes3.grid(True)
axes3.set_xscale('log')
axes3.set_ylim(0,max(Pyy_abs)*1.5)
axes3.set_xlim(20,20000)
axes3.set_title('{0:3.2f}'.format(time.time()-start_time))
axes3.set_title('{}'.format(np.round(fsk[:len(fsk)],decimals=1))+'\n'+'{}'.format(np.round(Psk[:len(fsk)],decimals=4)),size=10) #グラフのタイトルにピーク周波数とピーク強度を出力する
axes3.plot(fsk[:len(fsk)],Psk[:len(fsk)],'ro') #ピーク周波数、ピーク強度の位置に〇をつける
# グラフにピークの周波数をテキストで表示
for i in range(len(fsk)):
axes3.annotate('{0:.1f}'.format(fsk[i]),
xy=(fsk[i], Psk[i]),
xytext=(10, 20),
textcoords='offset points',
arrowprops=dict(arrowstyle="->",connectionstyle="arc3,rad=.2")
)
plt.pause(1)
wavfile=str(sec)+'_'+str(sk)
plt.savefig('./fft_sound/figure_'+wavfile+'_.jpg')
plt.clf()
freq,Pyy,fsk,Psk,f=FFT(sin_wave,fn,fr)
draw_pic(freq,Pyy,fsk,Psk,f,1,sin_wave,sec)
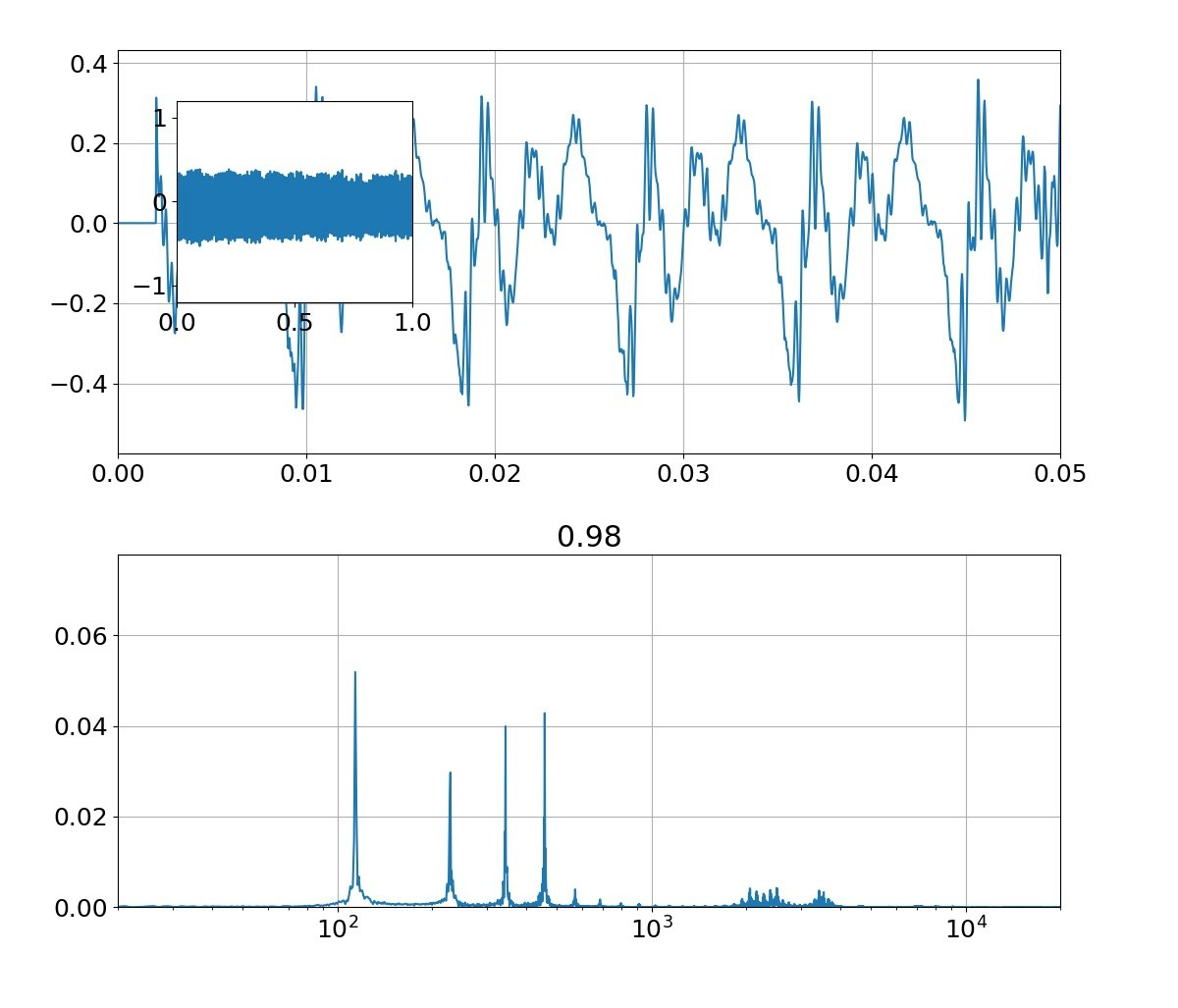
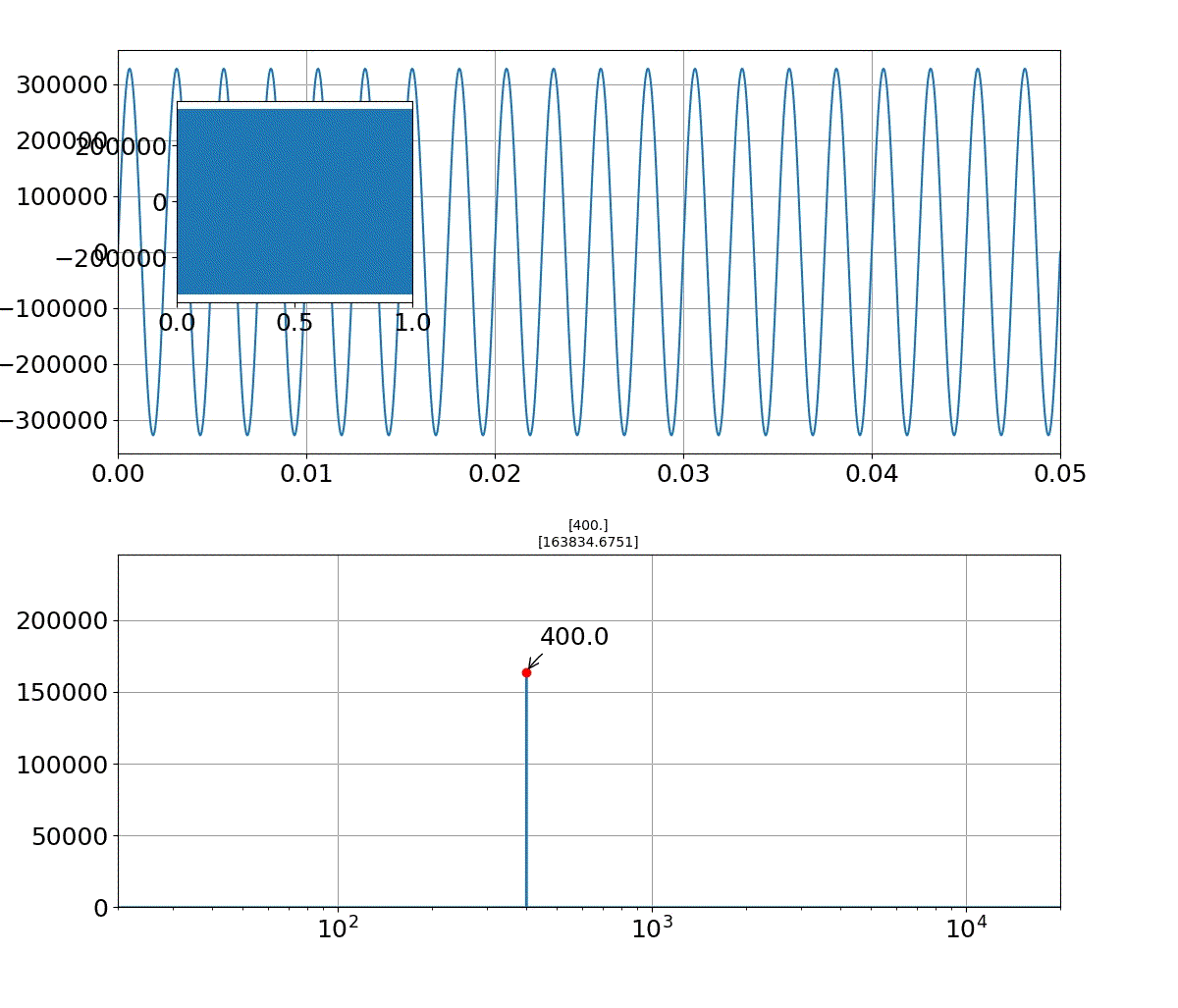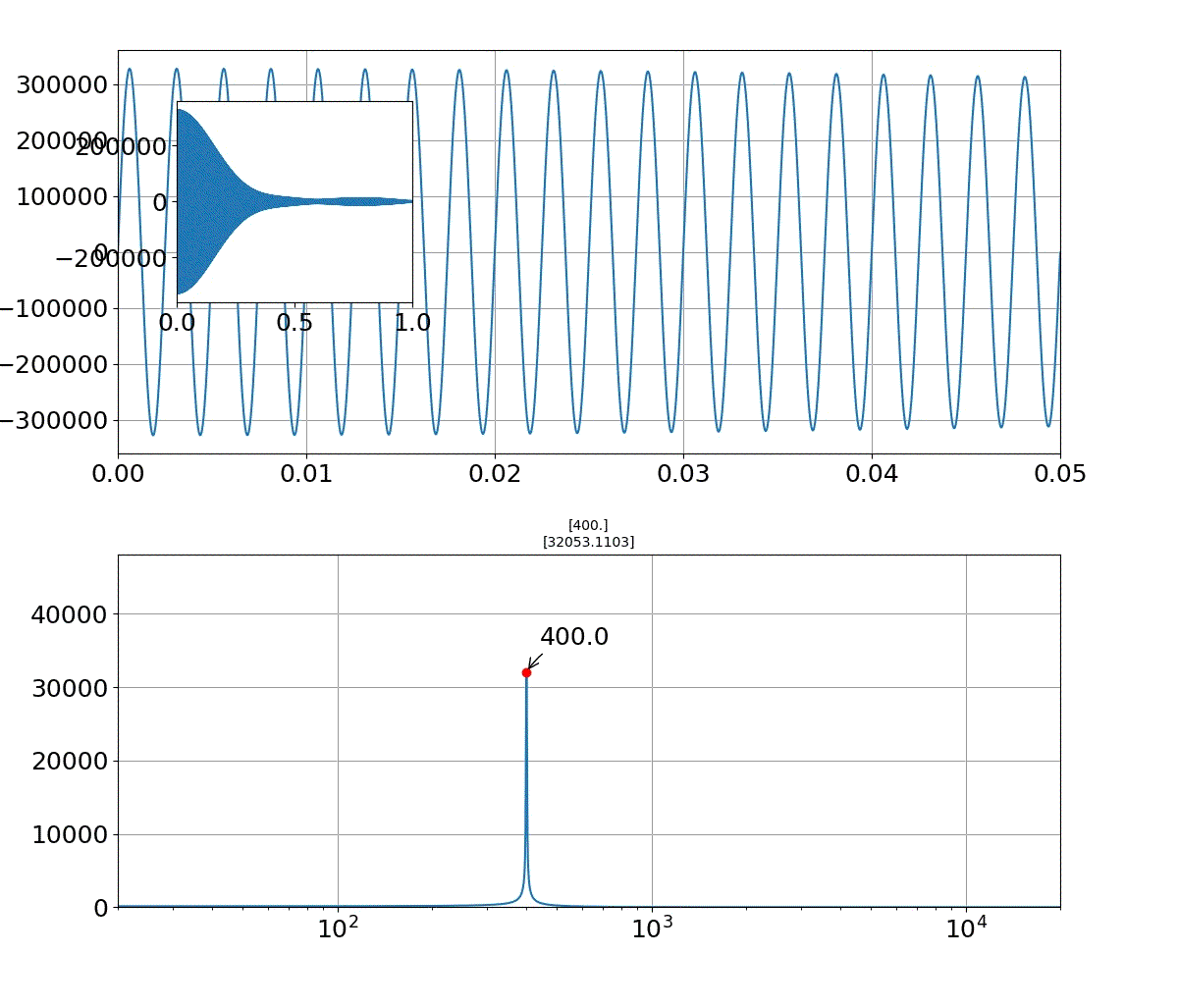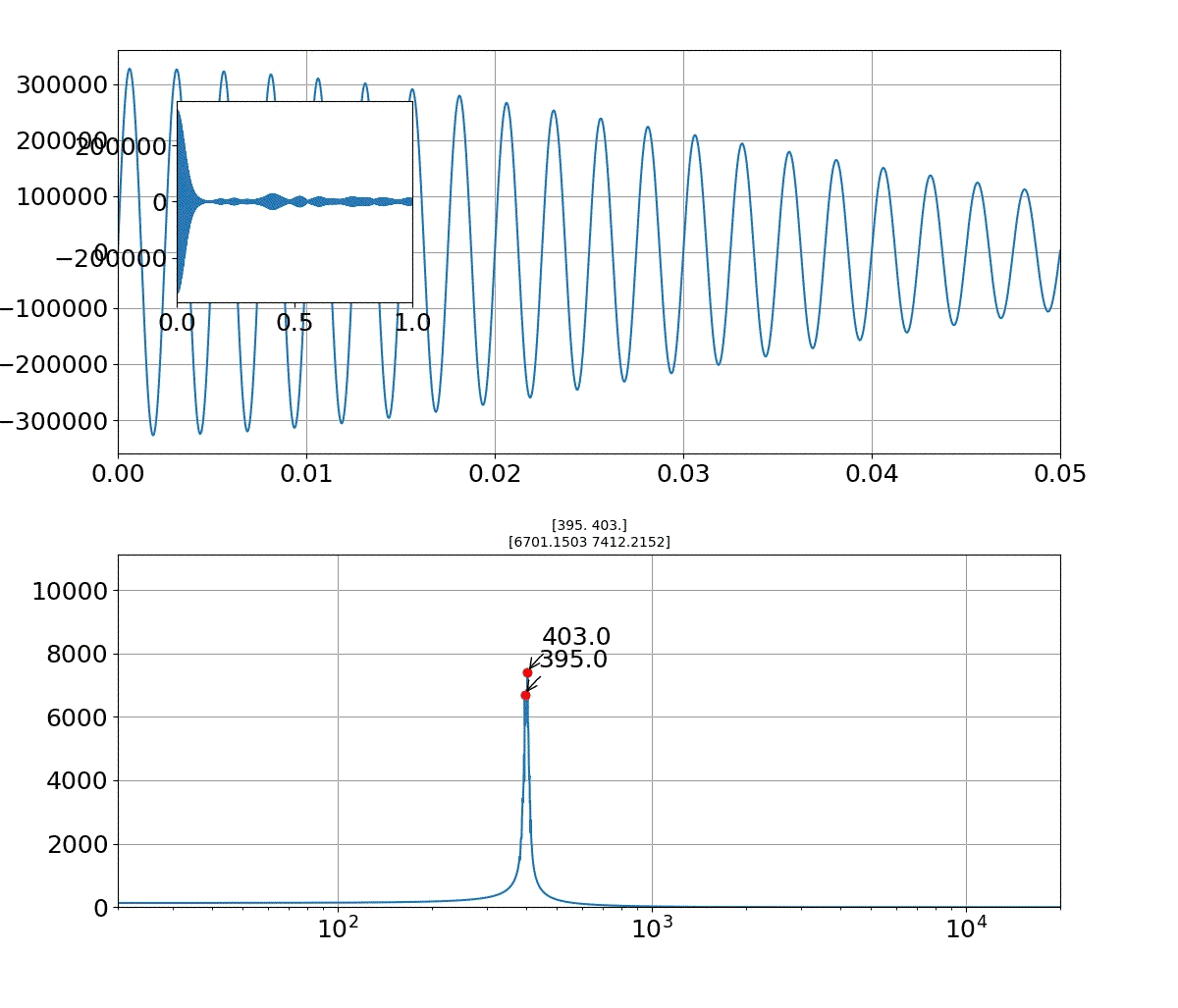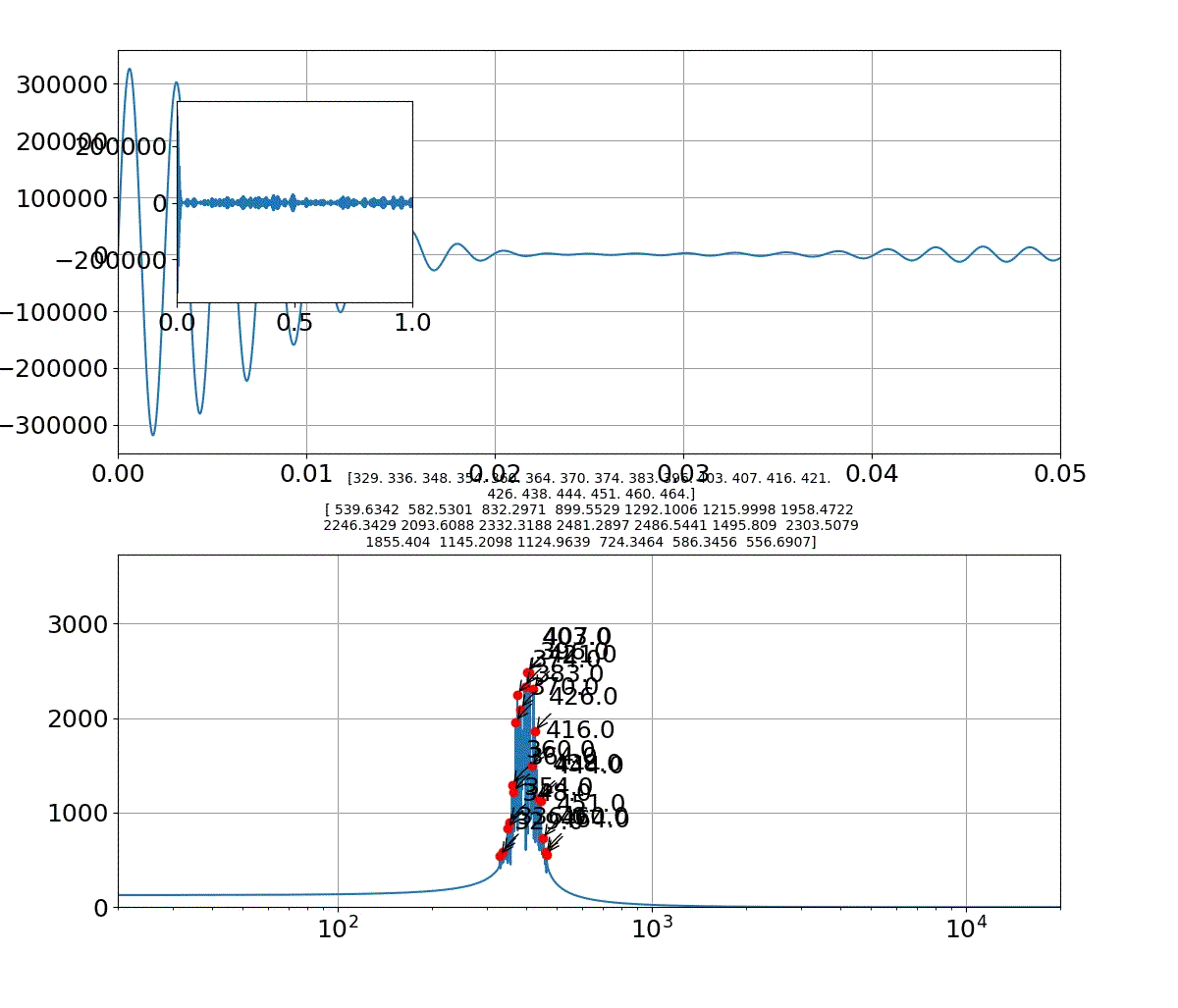
FFT図に以下のピークが表れる
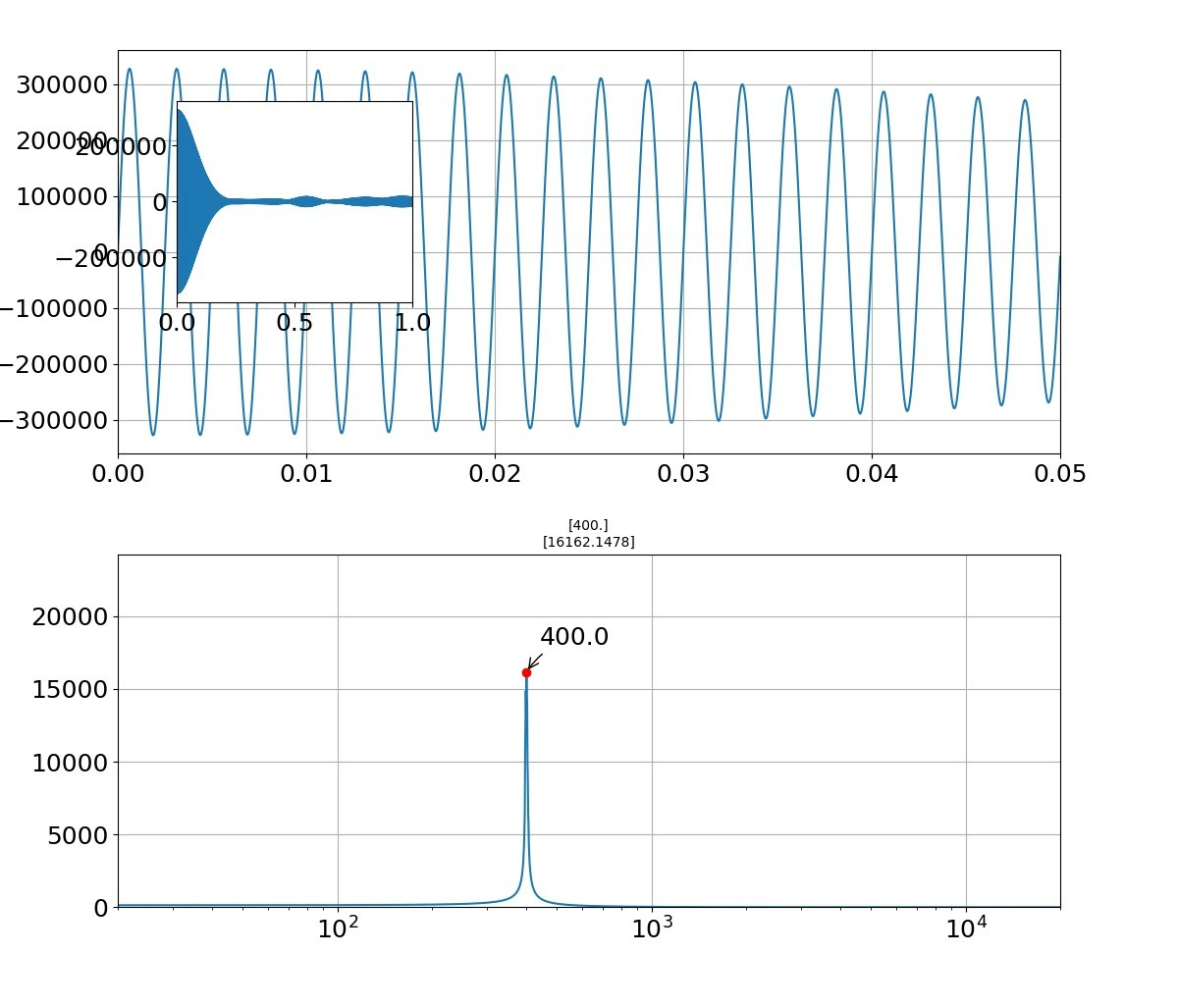
ピークの絶対値はちょっと大きいですが、一応綺麗な裾を持ったピークが現れました。
これは、上記のとおり1000回乱数を振った結果です。
そして、このサイン波を重畳したピークの特徴は、減衰が大きいということです。ただし、減衰した後は持続することもわかります。
また、減衰率は重畳する周波数の分布幅に依存することが分かりました。すなわち、分布幅を0,0.1,0.5,1,2,3,5,7,10,20と変化させたとき以下のように変化します。
・リアル音声のFFTとフォルマント合成音声のFFT図
コードは以下のおまけのとおりです。
今回はマイク入力の振動をFFTしてそのピークと周波数を利用して、サイン波を計算します。
したがって、流れはほとんと変わりません。
この結果として以下のような母音が発生できます。
※f0=f0+3*randn()としています
| 母音 | 音声 | 合成 |
|---|---|---|
| あ |  |
 |
| え |  |
 |
| い |  |
 |
| お |  |
 |
| う |  |
 |
| ここで、上記の単一ピーク作成ではサイン波の合成を1000回実施したが、実際の音声ではピーク数回数とした。これで一応ピークの裾を再現できている。これを多数回実施した場合もやってみたが、何が適正かを考えると結局裾のテールを再現すればよく、以下のコードで十分だという結論に到達した。 | ||
| ※ピークの数次第では、もっと多数回回した方がいい場合もあると思われるが、今回は以下のようにパラメータで再現している | ||
| ※一応、以下に10回回す場合のコードを掲載しておく |
def sin_wav(A,f0,fr,t):
point = np.arange(1000,fr*t+1000)
f0=f0 #+1*randn()
sin_wav =30*A* (np.sin(2*np.pi*f0*point/fr))
return sin_wav
def create_wave(A,f0,fr,t,wsk):#A:振幅,f0:基本周波数,fr:サンプリング周波数,再生時間[s]
sin_wave=0
for i in range(0,len(A),1):
for j in range(10):
f1=f0[i]+0.5*randn()
sw=sin_wav(A[i],f1,fr,t)
sin_wave += sw/10
...
※上記コードでpointの範囲の最初の点を1000ずらしているのは減衰項を考慮してサイン波の合成信号が減衰した後のものを採用している。このようにすることにより、0-0.05secの部分でも減衰が見えないこととなっている
まとめ
・フォルマント合成においてピークの裾状形状を基準周波数が正規分布したサイン波を取り入れることにより、より現実的な音声が再現できた
・連続するセンテンスに対しても応用できたので確立したいと思う
おまけ
import numpy as np
from matplotlib import pyplot as plt
import wave
import struct
import pyaudio
from scipy.fftpack import fft, ifft
import cv2
from scipy import signal
import matplotlib
import time
from numpy.random import *
# パラメータ
RATE=44100
sec =1 #秒
CHUNK=int(RATE*sec)
p=pyaudio.PyAudio()
sa= 'u' #'u' #'o' #'i' #'e' #'a'
stream=p.open(format = pyaudio.paInt16,
channels = 1,
rate = RATE,
frames_per_buffer = CHUNK,
input = True,
output = True) # inputとoutputを同時にTrueにする
fr = RATE #サンプリング周波数
fn=fr*sec
def sin_wav(A,f0,fr,t):
point = np.arange(1000,fr*t+1000)
f0=f0+3*randn()
sin_wav =30*A* (np.sin(2*np.pi*f0*point/fr))
return sin_wav
def create_wave(A,f0,fr,t,wsk):#A:振幅,f0:基本周波数,fr:サンプリング周波数,再生時間[s]
sin_wave=0
for i in range(0,len(A),1):
f1=f0[i]
sw=sin_wav(A[i],f1,fr,t)
sin_wave += sw
sin_wave = [int(x * 32767.0) for x in sin_wave]
binwave = struct.pack("h" * len(sin_wave), *sin_wave)
w = wave.Wave_write('./fft_sound/out_sin_'+str(sec)+'_'+str(wsk)+'.wav')
p = (1, 2, fr, len(binwave), 'NONE', 'not compressed')
w.setparams(p)
w.writeframes(binwave)
w.close()
def sound_wave(wsk):
wavfile = './fft_sound/out_sin_'+str(sec)+'_'+str(wsk)+'.wav'
wr = wave.open(wavfile, "rb")
input = wr.readframes(wr.getnframes())
output = stream.write(input)
sig =[]
sig = np.frombuffer(input, dtype="int16") /32768.0
return sig
t = np.linspace(0,sec, fn)
def FFT(sig,fn,fr):
freq =fft(sig,fn)
Pyy = np.sqrt(freq*freq.conj())/fn
f = np.arange(0,fr,fr/fn)
ld = signal.argrelmax(Pyy, order=3) #相対強度の最大な番号をorder=10で求める
ssk=0
fsk=[]
Psk=[]
maxPyy=max(np.abs(Pyy))
for i in range(len(ld[0])): #ピークの中で以下の条件に合うピークの周波数fと強度Pyyを求める
if np.abs(Pyy[ld[0][i]])>0.005*maxPyy and f[ld[0][i]]<20000 and f[ld[0][i]]>20:
fssk=f[ld[0][i]]
Pssk=np.abs(Pyy[ld[0][i]])
fsk.append(fssk)
Psk.append(Pssk)
ssk += 1
return freq,Pyy,fsk,Psk,f
matplotlib.rcParams.update({'font.size': 18, 'font.family': 'sans', 'text.usetex': False})
fig = plt.figure(figsize=(12,12)) #(width,height)
start_time=time.time()
def draw_pic(freq,Pyy,fsk,Psk,f,sk,sig,wsk):
axes1 = fig.add_axes([0.1, 0.55, 0.8, 0.4]) # main axes
axes2 = fig.add_axes([0.15, 0.7, 0.2, 0.2]) # insert axes
axes3 = fig.add_axes([0.1, 0.1, 0.8, 0.35]) # main axes
axes1.plot(t, sig)
axes1.grid(True)
axes1.set_xlim([0, 0.05])
axes2.set_ylim(-1.2,1.2)
axes2.set_xlim(0,sec)
axes2.plot(t,sig)
Pyy_abs=np.abs(Pyy)
axes3.plot(f,Pyy_abs)
#axes3.axis([min(fsk)*0.9, max(fsk)*1.1, 0,max(Pyy_abs)*1.5]) #0.5, 2
axes3.grid(True)
axes3.set_xscale('log')
axes3.set_ylim(0,max(Pyy_abs)*1.5)
axes3.set_xlim(20,20000)
axes3.set_title('{0:3.2f}'.format(time.time()-start_time))
plt.pause(0.001)
wavfile=str(sec)+'_'+sa+str(sk)
plt.savefig('./fft_sound/figure_'+wavfile+'_'+str(wsk)+'.jpg')
plt.clf()
wsk=0
while True:
input = stream.read(CHUNK)
sig =[]
sig = np.frombuffer(input, dtype="int16") /32768.0
#サイン波を-32768から32767の整数値に変換(signed 16bit pcmへ)
swav = [int(x * 32767.0) for x in sig]
#バイナリ化
binwave = struct.pack("h" * len(swav), *swav)
w = wave.Wave_write("./fft_sound/out_"+str(sec)+"_"+str(wsk)+".wav")
params = (1, 2, fr, len(binwave), 'NONE', 'not compressed')
w.setparams(params)
w.writeframes(binwave)
w.close()
#入力音声をFFTして描画する
freq,Pyy,fsk,Psk,f=FFT(sig,fn,fr)
draw_pic(freq,Pyy,fsk,Psk,f,1,sig,wsk)
#マイク入力を出力
input = binwave
output = stream.write(input)
#FFTで得られた周波数Pskと振幅fsk
A=Psk/max(Psk)/len(fsk)
f=fsk
#上記のAとｆを使ってサイン波でフォルマント合成
sigs =[]
create_wave(A, f, fr, sec,wsk)
sigs = sound_wave(wsk)
#フォルマント合成音声をFFTして描画する
freqs,Pyys,fsks,Psks,fss=FFT(sigs,fn,fr)
draw_pic(freqs,Pyys,fsks,Psks,fss,2,sigs,wsk)
wsk += 1