リーマン多様体上の無制約最適化問題に対する共役勾配法の紹介.
また,その Python での実装の紹介.
対象とする問題
リーマン多様体 $\mathcal{M}$ 上の無制約最適化問題
$$\mathop{\text{minimize}}_{x\in\mathcal M}\quad f(x)$$
を考える.ここで,$f:\mathcal M \to \mathbb R$ は滑らかな写像とする.
数空間上の共役勾配法
$\mathcal M = \mathbb R^n$ の場合の共役勾配法のアルゴリズムは以下の通り.
- $x^0$ を初期化する.
- $d^0=−\nabla f(x^0)$ で探索方向を初期化する.
- for $k=0,1,\ldots$ do
- ステップ幅 $t_k$ を計算する.
- $x^{k+1}=x^k+t_kd^k$ で更新する.
- $\beta_k=\frac{\nabla f(x^{k+1})^\top \nabla f(x^{k+1})}{\nabla f(x^k)^\top \nabla f(x^k)}$ を計算する.
- $d^{k+1}=−\nabla f(x^{k+1})+\beta_kd^k$ で探索方向を更新する.
- end for
詳細には前の記事に記述した.
リーマン多様体上の共役勾配法 [Absil et al. 2009]
$\mathcal M$ がリーマン多様体の場合の共役勾配法のアルゴリズムは, Absil らの多様体上の最適化の書籍 "Optimization Algorithms on Matrix Manifolds" にて紹介されている.
- $x^0$ を初期化する.
- $d^0=−\color{red}{\mathop{\mathrm{grad}}} f(x^0)$ で探索方向を初期化する.
- for $k=0,1,\ldots$ do
- ステップ幅 $t_k$ を計算する.
- $x^{k+1}=\color{red}{R_{x^k}}\left(t_kd^k\right)$ で更新する.
- $\beta_k=\frac{\left\langle\mathop{\mathrm{grad}}f(x^{k+1}),\mathop{\mathrm{grad}}f(x^{k+1})\right\rangle_{\color{red}{x^{k+1}}}}{\left\langle\mathop{\mathrm{grad}}f(x^{k}),\mathop{\mathrm{grad}}f(x^{k})\right\rangle_{\color{red}{x^{k}}}}$ を計算する.
- $d^{k+1}=−\mathop{\mathrm{grad}} f(x^{k+1})+\beta_k\color{red}{\mathcal T_{t_kd^k}}(d^k)$ で探索方向を更新する.
- end for
数空間 $\mathbb R^n$ の場合と比較して,赤文字の箇所が大きく異なっている.
以下でそれぞれ解説していく.
リーマン多様体上の内積
リーマン多様体 $\mathcal M$ では,リーマン計量により,任意の点 $x\in\mathcal M$ における接空間 $T_x\mathcal M$ 上に正定値な内積 $\langle\cdot,\cdot\rangle_x$ が定まっている.
リーマン多様体上の勾配
$\mathcal M = \mathbb R^n$ のとき,$f$ の勾配は
$$\nabla f(x) := \left(\frac{\partial f}{\partial x_1}(x), \frac{\partial f}{\partial x_2}(x), \ldots, \frac{\partial f}{\partial x_n}(x)\right)^\top$$
で計算できる.このとき,勾配と方向微分の間に
$$\mathop{\mathrm D}f(x)[d] := \frac{\mathrm d}{\mathrm dt}f(x+td) = \nabla f(x)^\top d$$
の関係が成立する.
リーマン多様体 $\mathcal M$ 上関数 $f$ の $d$ 方向微分は,$\gamma(0)=x$ かつ $\dot\gamma(0) = d$ となる曲線 $\gamma:\mathbb R \to \mathcal M$ を用いて
$$\mathop{\mathrm D}f(x)[d] := \frac{\mathrm d}{\mathrm dt}f(\gamma(t))$$
で計算できる.この方向微分を用いて,関数 $f$ のリーマン多様体上の勾配 $\mathop{\mathrm{grad}}f$ を
$$\mathop{\mathrm{D}} f(x)[d] = \langle \mathop{\mathrm{grad}} f(x), d\rangle_x$$
をみたす $T_x\mathcal M$ 上の元として定義する.
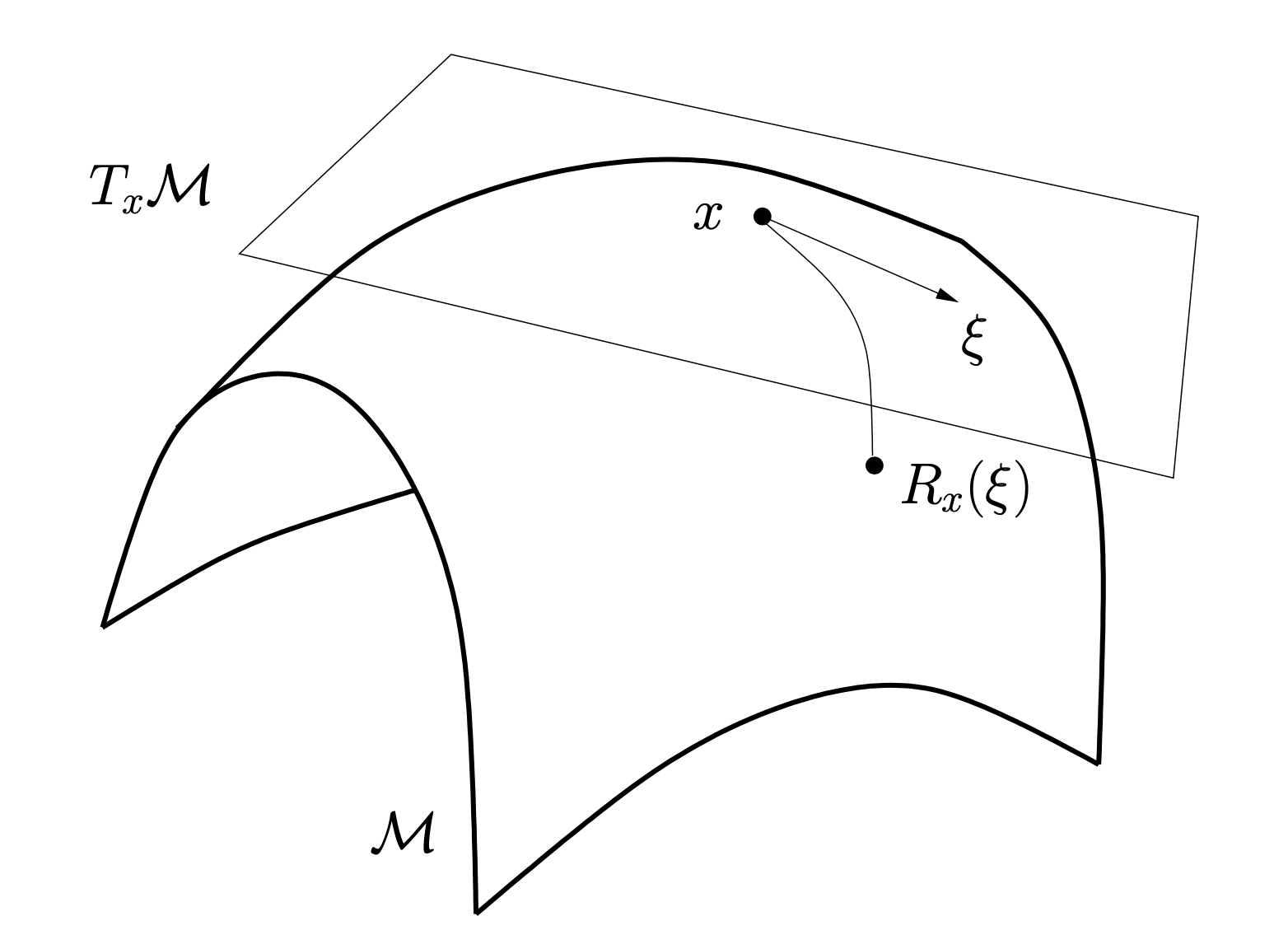
レトラクション
リーマン多様体 $\mathcal M$ における変数の更新式において,$x^k\in\mathcal M$ に対し $d^k \in T_{x^k}\mathcal M$ であり,属する空間が異なるため,単純な加法 $x^{k+1} = x^k + t_k d^k$ で更新することはできない.
そこで,自然な拡張としては,リーマン多様体上の直線 (加速度が 0) にあたる測地線に沿った更新が考えられる.初期点 $\gamma(0) = x$ かつ初速度 $\dot\gamma(0) = \xi$ なる測地線を $\gamma(t;x, \xi)$ とすると,
$$x^{k+1}=\gamma(t_k;x^k,d^k)=:\exp_{x^k}(t_kd^k)$$
で更新することができる.ここで,$\exp:T\mathcal M \to \mathcal M$ は指数写像と呼ばれる写像である.
リーマン多様体上の最適化の分野では,指数写像をより一般化したレトラクションと呼ばれる写像を用いて,
$$x^{k+1}=R_{x^k}(t_kd^k)$$
で変数を更新する.レトラクションは,以下の2条件を満たす接束 $T\mathcal M$ から $\mathcal M$ への滑らかな写像である.
- $R_x(0_x) = x\qquad$($0_x$ は $T_x\mathcal M$ 上の零ベクトル)
- $\mathop{\mathrm{D}}R_x(0_x) = \mathrm{id}_{T_x\mathcal M}\qquad$($\mathrm{id}$ は恒等写像)
ベクトル輸送
$\mathbb R^n$ 上の共役勾配法の探索方向の更新式をリーマン多様体 $\mathcal M$ に拡張するとき,そのまま
$$d^{k+1}=−\mathop{\mathrm{grad}} f(x^{k+1})+\beta_kd^k$$
とすることはできない.これは,$\mathop{\mathrm{grad}} f(x^{k+1})\in T_{x^{k+1}}\mathcal M$ と $d^k\in T_{x^k}\mathcal M$ の属する接空間が異なるためである.
そこで,自然な拡張としては,$d^k\in T_{x^k}\mathcal M$ を $T_{x^{k+1}}\mathcal M$ の元へと平行移動することである.ここでいう平行とは,ある曲線 (例えば測地線 $\gamma(t;x^k, d^k)$) に沿ったベクトル場が平行であることをいう.
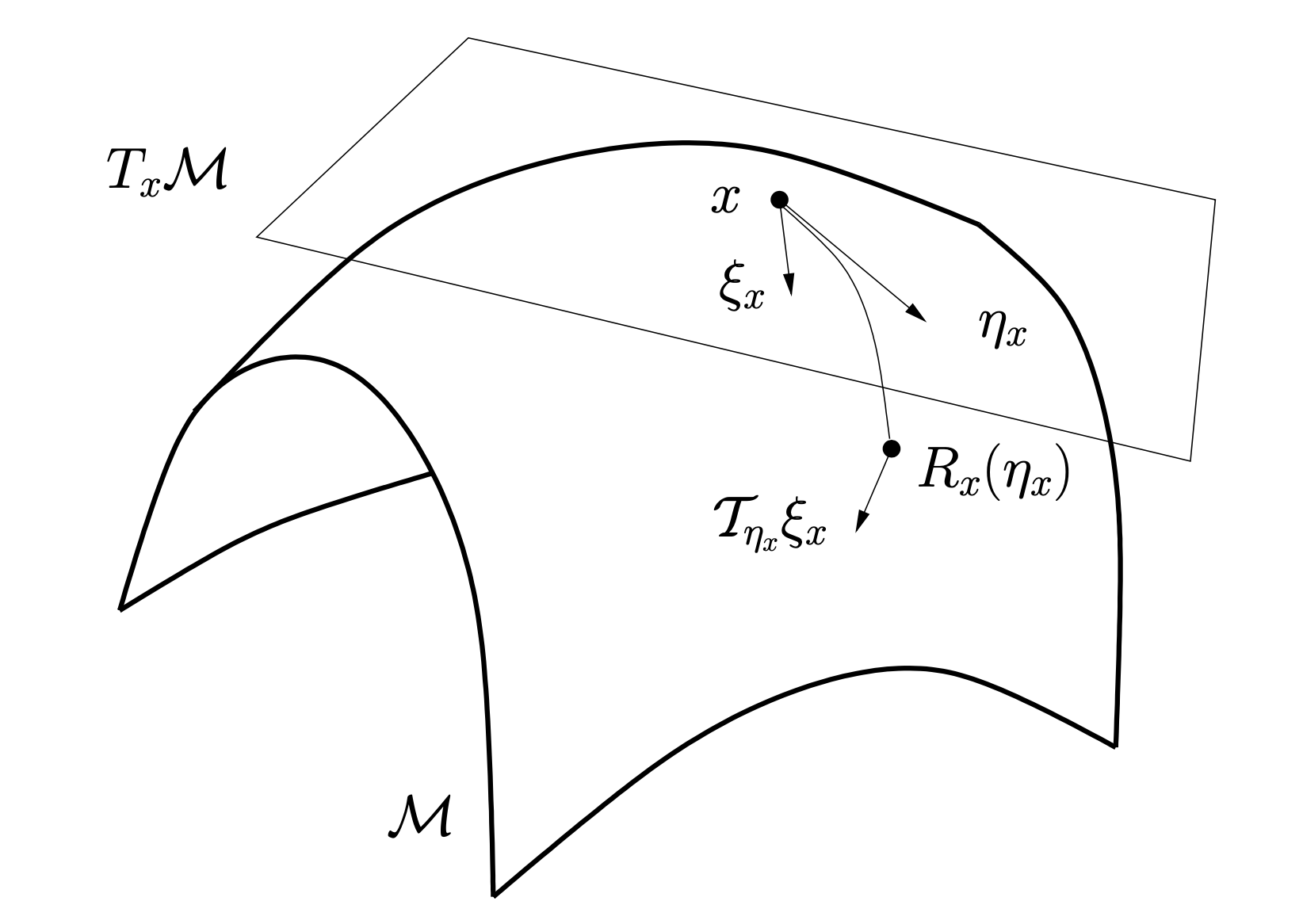
リーマン多様体上の最適化の分野では,平行移動をより一般化したベクトル輸送と呼ばれる写像 $\mathcal T$ を用いて,
$$d^{k+1}=−\mathop{\mathrm{grad}} f(x^{k+1})+\beta_k\mathcal T_{t_kd^k}(d^k)$$
で探索方向を更新する.ベクトル輸送 $\mathcal T_{\eta_x}$ とは, $T_x\mathcal M$ 上の接ベクトル $\xi_x$ を $T_{R_x(\eta_x)}$ 上の接ベクトル $\mathcal T_{\eta_x}{\xi_x}$ に写す写像で,次の2条件を満たすものである.
- $\mathcal T_{0_x}(\xi_x) = \xi_x$
- $\mathcal T_{\eta_x}(a\xi_x + b\zeta_x) = a\mathcal T_{\eta_x}(\xi_x) + b\mathcal T_{\eta_x}(\zeta_x)$
Python での実装
Python では,Pymanopt というリーマン多様体上の最適化のソルバーが実装されている.その中でも,pymanopt.solvers.conjugate_gradient.ConjugateGradient に共役勾配法が実装されている.
使用例
問題
次の Brockett cost function の最小化問題を考える.
\begin{align}
\mathop{\mathrm{minimize}}_{X\in \mathbb R^{n \times r}} &\quad f(X) :=\mathop{\mathrm{tr}}\left(X^\top A X N\right)\\
\text{subject to} &\quad X^\top X = I_r
\end{align}
ここで,$A\in\mathbb{R}^{n\times n}$ は対称行列,$N\in\mathbb{R}^{r\times r}$ は正値の対角行列 $N = \mathop{\mathrm{diag}}(\mu_1, \mu_2, \ldots, \mu_r)$ で,$0<\mu_1\leq\mu_2\leq\dots\leq\mu_r$ をみたす.最適解 $X_*$ は $A$ の小さい順から $r$ 個の固有値に対応する固有ベクトルを並べた行列となっている.また,ユークリッド空間における $f$ の勾配は,
$$\nabla f(X) = 2AXN$$
で計算される.
この最適化問題は,シュティーフェル多様体
\mathop{\mathrm{St}}(n, r) := \left\{X\in\mathbb{R}^{n\times r} \mid X^\top X = I_r\right\}
上の無制約最適化問題
\mathop{\mathrm{minimize}}_{X \in \mathop{\mathrm{St}}(n, r)} \quad f(X)
へと変換することができる.
実行例
対称行列 $A$ を以下で生成する.
import numpy as np
n = 10
r = 3
np.random.seed(0)
A = np.random.randn(n, n)
A = 0.5 * (A + A.T)
pymanopt.solvers.conjugate_gradient.ConjugateGradient を使用するには,pymanopt.core.problem.Problem を設定する必要がある.設定の仕方は公式に記載があるが,今回はその中でも,Python の関数で目的関数とその勾配 (ユークリッド空間) を指定する方法を採用する.この方法では,内部でユークリッド空間上の勾配 $\nabla f$ からシュティーフェル多様体上の勾配 $\mathop{\mathrm{grad}}f$ へと変換される.
class Brockett:
def __init__(self, A: np.ndarray, r: int):
if A.ndim != 2:
raise ValueError(f'Expected 2D array, got {A.ndim}D array instead.')
self.A = A
r = np.minimum(r, A.shape[0])
self.N = np.arange(1, r + 1) / r
def cost(self, X: np.ndarray) -> float:
return np.sum((self.A @ X) * (X * self.N))
def egrad(self, X: np.ndarray) -> np.ndarray:
return 2 * self.A @ X * self.N
上記で定義した Brockett cost function のクラスを使用して,Pymanopt の Problem を次のように設定する.
from pymanopt import Problem
from pymanopt.manifolds import Stiefel
brockett = Brockett(A=A, r=r)
stiefel = Stiefel(n, r)
prob = Problem(manifold=stiefel, cost=brockett.cost, egrad=brockett.egrad)
ConjugateGradient では $\beta$ の種類を指定することができる.今回は beta_type=0 (Fletcher-Reeves) を使用した.また,solve 関数では問題に加えて,初期点を指定することもできる.今回は $X_0 = (I_r, O)^\top$ を初期行列とした.
from pymanopt.solvers import ConjugateGradient
X0 = np.eye(n, r)
solver = ConjugateGradient(beta_type=0)
Xopt = solver.solve(prob, x=X0)
得られた解の正しさは,numpy.linalg.eigh の結果と比較することで確かめられる.
_, V = np.linalg.eigh(A)
print(np.sum(Xopt * V[:, :r][:, ::-1], axis=0)) # [1. 1. 1.]