カメラキャリブレーションとは
カメラキャリブレーションとは3Dコンピュータビジョンにおいて2D画像からメトリック情報を抽出するために適切なカメラのモデルパラメータを推定する処理である。簡単に言えばカメラが持つ固有の誤差を推定し、その誤差が小さくなるように画像を修正する処理のことである。(注.この記事ではピンホールカメラのみ対象とする)
理論
理想的なカメラモデル
まず、カメラキャリブレーションを論ずる前に撮影対象が画像に焼き付けられる様子を数式に落とし込む。これをカメラモデルと呼ぶ
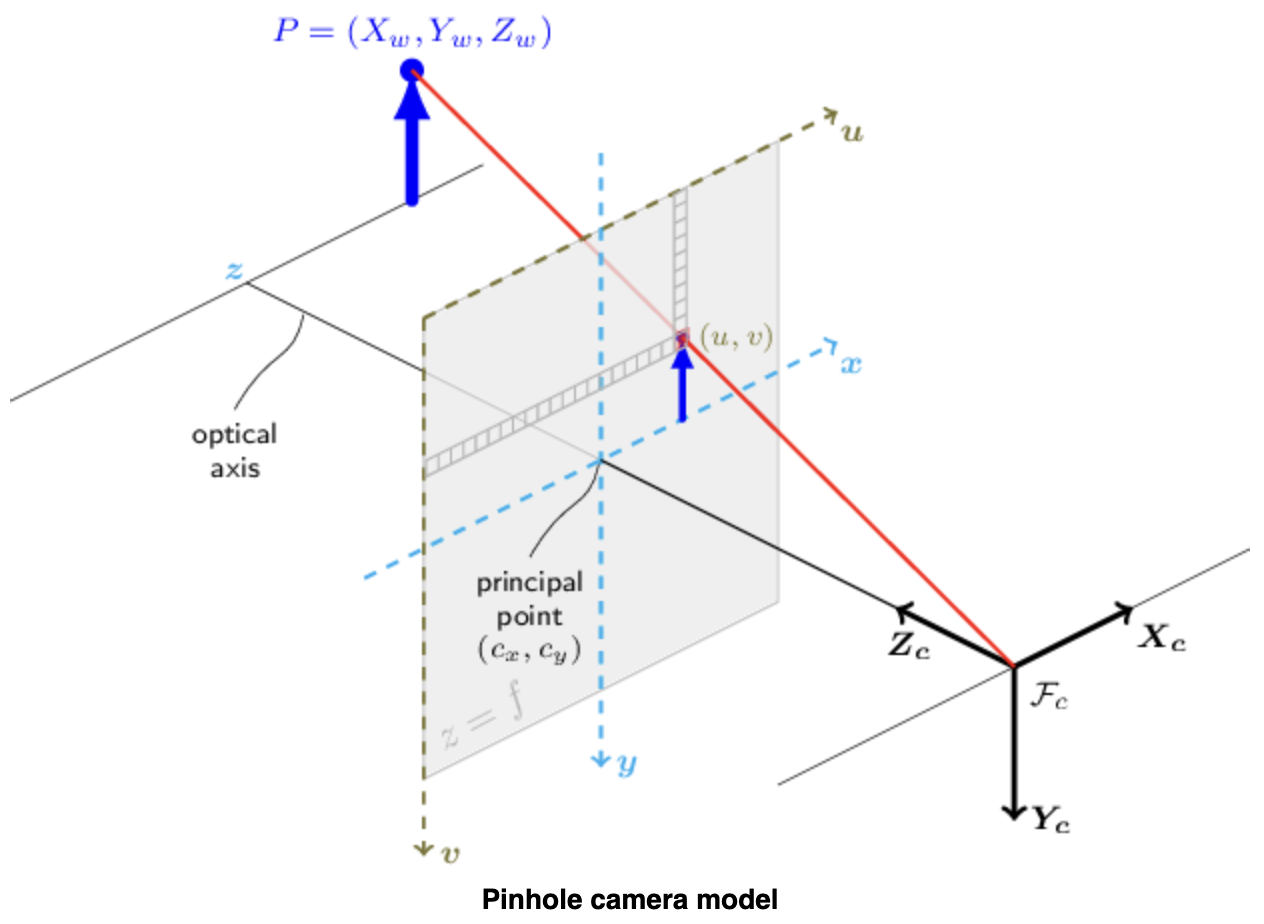
3つの座標系を用いてカメラモデルを記述する。1つはワールド座標系$P_w=(X_w, Y_w, Z_w)$、撮影対象(人や花などなんでも)の座標を記述するための座標系。2つ目はピクセル座標系$p=(u, v)$、我々がスマホやカメラで見る写真の座標系。最後に2つの座標系を中継するためのカメラ座標系$P_c=(X_c, Y_c, Z_c)$である。
撮影とは透視変換(Perspective Transformation)を用いて撮影対象の3次元点$P_w$を対応するピクセル$p$に投影することであり、
sp=A[R|t]P_w
と表される。ここで$P_w$はワールド座標系における3次元点、$p$はピクセル座標系における2次元点、$A$はカメラ固有行列(通称カメラ行列)、$R$と$t$はワールド座標系からカメラ座標系への座標変換を表す回転と並行移動、sは透視変換の任意のスケーリングでありカメラモデルの一部ではない(つまり考えなくていい)。
カメラ固有行列$A$はカメラ座標系の3次元点とピクセル座標系の2次元点を投影する行列である。
p=AP_c
s\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}f_x&0&c_x\\0&f_y&c_y\\0&0&1\end{bmatrix}\begin{bmatrix}X_c\\Y_c\\Z_c\end{bmatrix}
ここで$f_x, f_y$は焦点距離、$c_x, c_y$は主点(基本的に画像の中心点)を示す。
回転-並行移動合同行列$[R|t]$は透視変換と同次変換の行列積であり、ワールド座標系からカメラ座標系への投影を表す。
P_c=\begin{bmatrix}R&t\\0&1\end{bmatrix}P_w
\begin{bmatrix}X_c\\Y_c\\Z_c\\1\end{bmatrix}=\begin{bmatrix}r_{11}&r_{12}&r_{13}&t_x\\r_{21}&r_{22}&r_{23}&t_y\\r_{31}&r_{32}&r_{33}&t_z\\0&0&0&1\end{bmatrix}\begin{bmatrix}X_w\\Y_w\\Z_w\\1\end{bmatrix}
ここで$[R|t]$は$3\times3$の回転行列$R$と$3\times1$の並進ベクトル$t$からなる
\begin{bmatrix}R&t\\0&1\end{bmatrix}=\begin{bmatrix}r_{11}&r_{12}&r_{13}&t_x\\r_{21}&r_{22}&r_{23}&t_y\\r_{31}&r_{32}&r_{33}&t_z\\0&0&0&1\end{bmatrix}
よって$sp=A[R|t]P_w$は
s\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}f_x&0&c_x\\0&f_y&c_y\\0&0&1\end{bmatrix}\begin{bmatrix}r_{11}&r_{12}&r_{13}&t_x\\r_{21}&r_{22}&r_{23}&t_y\\r_{31}&r_{32}&r_{33}&t_z\end{bmatrix}\begin{bmatrix}X_w\\Y_w\\Z_w\\1\end{bmatrix}
とかける。また、もし$Z_c$が0でない場合、上式は
\begin{bmatrix}u\\v\end{bmatrix}=\begin{bmatrix}f_xX_c/Z_c+c_x\\f_yY_c/Z_c+c_y\end{bmatrix}
と書き直すことができる。ここで$P_c$は
\begin{bmatrix}X_c\\Y_c\\Z_c\end{bmatrix}=[R|t]\begin{bmatrix}X_w\\Y_w\\Z_w\\1\end{bmatrix}
現実のカメラモデル
しかし、実際のレンズは歪みを持つ。この歪みはほとんどが放射状歪み(Radial Distortion)でわずかに接線歪み(Tangential Distortion)である。
そこでこれらの歪みから上式は
\begin{bmatrix}u\\v\end{bmatrix}=\begin{bmatrix}f_xx''+c_x\\f_yy''+c_y\end{bmatrix}
where
\begin{bmatrix}x''\\y''\end{bmatrix}=\begin{bmatrix}x'\frac{1+k_1r^2+k_2r^4+k_3r^6}{1+k_4r^2+k_5r^4+k_6r^6}+2p_1x'y'+p_2(r^2+2x'^2)+s_1r^2+s_2r^4\\
y'\frac{1+k_1r^2+k_2r^4+k_3r^6}{1+k_4r^2+k_5r^4+k_6r^6}+p_1(r^2+2y'^2)+2p_2x'y'+s_3r^2+s_4r^4
\end{bmatrix}
r^2=x'^2+y'^2
\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}X_c/Z_c\\Y_c/Z_c\end{bmatrix}
と変形される。ここで$k_1, k_2, k_3, k_4, k_5, k_6$は放射状歪みを司る歪み係数、$p_1, p_2$は接線歪みに関わる歪み係数、$s_1, s_2, s_3, s_4$はプリズム歪み係数である。
問題の定式化
長々と書いたが要するに上の歪み係数を求めることができれば現実のカメラを理想のカメラに近づけることができる。歪み係数を求めるにはZhangが提案した手法[5]を用いる。まず、ワールド座標$M=(x, y, z)$とピクセル座標$m=(u, v)$の現実のペアをたくさん集める。(要するにたくさん撮影する)。次にワールド座標$M$の理論的なピクセル座標$\hat{m}=(\hat{u}, \hat{v})$を求める。そして$m$と$\hat{m}$の差が最小になるような歪み係数を
argmin\Sigma_{i=1}^n\Sigma_{j=1}^m||m_{ij} - \hat{m}(A, R_i, t_i, M_j)||^2
で求める。この最適化方程式を歪み係数とカメラパラメータについて解く。
解法
上式についてはLevenberg-Marquardt Algorithm[4]を解法として用いる。この解法は微分可能な制約なし非線形最小二乗問題を解くためのものである。最急勾配法とガウスニュートン法の折衷案のような方法であり、アルゴリズム
\textbf{x}_{k+1} = \textbf{x}_k - (\textbf{J}_k^T\textbf{J}_k+\lambda\textbf{I})^{-1}\textbf{J}_k^T\textbf{r}_k
に従って反復計算を繰り返すことで解に近づけていく。
補正
最後に得られた歪み係数$(k_1,k_2,p_1,p_2,k_3)$を用いて補正後のピクセル座標$u_{distorted},v_{distorted}$は放射状歪みについて
\begin{equation}
\begin{split}
u_{distorted} &= u(1+k_1r^2+k_2r^4+k_3r^6)\\
v_{distorted} &= v(1+k_1r^2+k_2r^4+k_3r^6)
\end{split}
\end{equation}
接線歪みについて
\begin{equation}
\begin{split}
u_{distorted} &= u+[2p_1uv+p_2(r^2+2x^2)]\\
v_{distorted} &= v+[p_1(r^2+2y^2)+2p_2uv]
\end{split}
\end{equation}
where
r=\sqrt{u^2+v^2}
実装
長々と理論について書いてきたがpythonではopencvを用いて理論を理解せずとも簡単に実装することができる。以下にフローを示す。
チェスボードの用意
モノクロのチェスボード1枚を[3]を用いて印刷して板に貼り付けた。そしてチェスボードの1マスの大きさを測定した。
撮影
キャリブレーションを施すカメラを用いてstep1で作成したチェスボードを姿勢を変えながら複数回撮影した。(特に決まりはないが10枚以上が推奨されている)

プログラム
下記コードを作成し、撮影した画像にキャリブレーションを施した。
class CameraCalibration:
def __init__(self):
self.corners_num = (3, 4)
self.square_size = 10
self.criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, self.square_size, 0.001)
self.img_path = "path/to/img/"
self.img_extension = ".tiff"
self.obj_points = []
self.img_points = []
self.images = []
self.obj_point = np.zeros((3 * self.corners_num[1], self.corners_num[0]), np.float32)
self.obj_point[:, :2] = np.mgrid[0:self.corners_num[1], 0:self.corners_num[0]].T.reshape(-1, 2)
self.found_images = []
self.not_found_images = []
self.error = []
self.camera_mtx = np.zeros((3, 3))
self.dist_coef = np.zeros((3, 3))
self.rotational_vec = np.zeros((3, 3))
self.translational_vec = np.zeros((3, 3))
self.new_camera_mtx = np.zeros((3, 3))
def set_corners_num(self, corners_num):
self.corners_num = corners_num
self.obj_point = np.zeros((3 * self.corners_num[1], self.corners_num[0]), np.float32)
self.obj_point[:, :2] = np.mgrid[0:self.corners_num[1], 0:self.corners_num[0]].T.reshape(-1, 2)
def set_square_size(self, square_size):
self.square_size = square_size
self.criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, self.square_size, 0.001)
def set_img_path(self, img_path):
self.img_path = img_path
def set_img_extension(self, img_extension):
self.img_extension = img_extension
def set_images(self):
self.images = sorted(glob.glob(self.img_path + '*' + self.img_extension))
def convert_rgb2gray(self, img):
img_rgb = plt.imread(img)
plt.gray()
img_bgr = cv2.cvtColor(img_rgb, cv2.COLOR_RGB2BGR)
img_gray = cv2.cvtColor(img_bgr, cv2.COLOR_BGR2GRAY)
return img_gray
def calc_reprojection_err(self):
for i in range(len(self.obj_points)):
reprojected_imgpoint, _ = cv2.projectPoints(self.obj_points[i], self.rotational_vec[i],
self.translational_vec[i],
self.camera_mtx, self.dist_coef)
error = cv2.norm(self.img_points[i], reprojected_imgpoint, cv2.NORM_L2) / len(reprojected_imgpoint)
self.error.append(error)
def find_corners(self, img):
found, corners = cv2.findChessboardCorners(img, (self.corners_num[1], self.corners_num[0]), None)
return found, corners
def find_accurate_corners(self, found, img, corners, img_name):
if found:
self.found_images.append(img_name)
self.obj_points.append(self.obj_point)
accurate_corners = cv2.cornerSubPix(img, corners, (11, 11), (-1, -1), self.criteria)
self.img_points.append(accurate_corners)
else:
self.not_found_images.append(img_name)
def calibrate(self, img):
_, self.camera_mtx, self.dist_coef, self.rotational_vec, self.translational_vec = cv2.calibrateCamera(
self.obj_points, self.img_points, img.shape[::-1], None, None
)
def get_new_camera_mtx(self, img):
self.new_camera_mtx, _ = cv2.getOptimalNewCameraMatrix(self.camera_mtx, self.dist_coef,
(img.shape[1], img.shape[0]), 1,
(img.shape[1], img.shape[0]))
def view_result(self):
found_img_rate = len(self.found_images) / len(self.images)
not_found_img_rate = len(self.not_found_images) / len(self.images)
found_img_label = [found_image.split('/')[-1] for found_image in self.found_images]
pie_color = ["gray", "black"]
print(f"Number of Images : {len(self.images)}\n"
f"Number of Found Images : {len(self.found_images)}")
pprint.pprint(self.found_images)
print(f"Number of Not Found Images : {len(self.not_found_images)}")
pprint.pprint(self.not_found_images)
print(f"Found Rate : {found_img_rate*100:.1f}%\n"
f"Mean Reprojection Error : {np.mean(self.error):.3f}")
plt.pie([found_img_rate, not_found_img_rate], labels=['Found', 'Not Found'], autopct='%1.1f%%', startangle=90, colors=pie_color)
plt.title('Found Rate')
plt.show()
plt.barh(found_img_label, self.error, color='black')
plt.title('Reprojection Error')
plt.tight_layout()
plt.show()
def save_params(self):
mtx_df = pd.DataFrame(self.camera_mtx)
dist_df = pd.DataFrame(self.dist_coef)
newcameramtx_df = pd.DataFrame(self.new_camera_mtx)
mtx_df.to_csv('mtx.csv', index=None, header=None)
dist_df.to_csv('dist.csv', index=None, header=None)
newcameramtx_df.to_csv('newcameramtx.csv', index=None, header=None)
corners_num = (3, 4) # 検出する角の数(x, y)
square_size = 10 # チェスボードの1マスの大きさ[mm]
path = "path to image" # キャリブレーションを施す画像が格納されているパス
extension = ".tiff" # 画像の拡張子
def main():
cc = CameraCalibration()
cc.set_corners_num(corners_num)
cc.set_square_size(square_size)
cc.set_img_path(path)
cc.set_img_extension(extension)
cc.set_images()
for img in tqdm(cc.images):
img_gray = cc.convert_rgb2gray(img)
found, corners = cc.find_corners(img_gray)
cc.find_accurate_corners(found, img_gray, corners, img)
cc.calibrate(img_gray)
cc.get_new_camera_mtx(img_gray)
cc.calc_reprojection_err()
cc.view_result()
cc.save_params()
if __name__ == '__main__':
main()
評価
上のプログラムから得られた結果を評価する。まず角を検出することができた画像は26枚中5枚であった。

少なめなので増やす必要がある。
次に本題のキャリブレーションの精度を確認した。評価方法は再投影誤差を用いた。再投影誤差は二乗平均平方根誤差の画像に適用したものである。
RMSE = \sqrt{\frac{\Sigma_i^N{(\hat{y}_i-y_i)^2}}{N}}
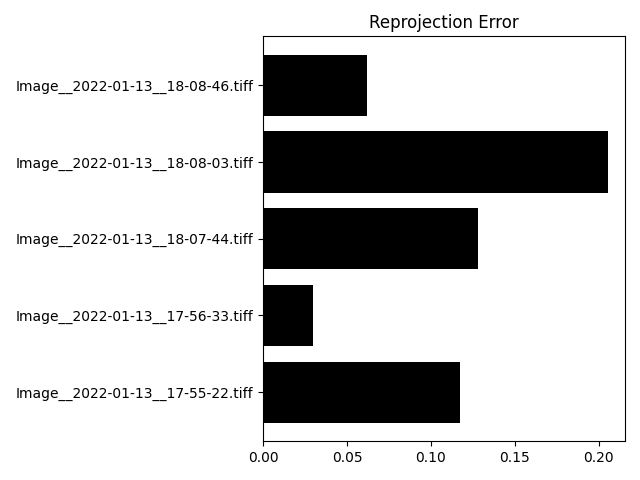
ここで$\hat{y}_i$はキャリブレーション後にチェスボード角をピクセル座標系に投影した時のノルム、$y_i$はキャリブレーション前にチェスボード角をピクセル座標系に投影した時のノルム、$N$は画像1枚あたりの角の数である。結果を以下に示す。
参考文献
[1]OpenCV. "Camera Calibration and 3D Reconstruction". https://docs.opencv.org/3.4/d9/d0c/group__calib3d.html
[2]OpenCV. "Camera Calibration". https://docs.opencv.org/4.x/dc/dbb/tutorial_py_calibration.html
[3]めめんと. "チェスボード画像自動生成ツール". http://shouginekochann.blog9.fc2.com/blog-entry-33.html?sp
[4]G.A.Watson. Numerical Analysis. Springer.
[5]Zhengyou Zhang. A Flexible New Technique for Camera Calibration.
