ABC269をPythonとC++で

0 はじめに

0-1 記事について

AtCoder Beginner Contest 269の解説です。
実装はPythonとC++で書きます。
C++での実装はこの記事の最後にあります。
公式解説と違いがあるかも知れませんがご了承。
ミス等発見されましたらコメント欄にお願いします。

1 ABC269 解説

1-1 個人的な感想

今回は崖が激しかったように思います。
Diffは、AとBが灰前半、Cが灰と茶の中間、Dが茶後半、Eが緑後半、F (解いてない) が青前半といった感じです。
私は40分程で五冠し、Perfが1450程で、Ratingは1162→1194(+32)でした。
折角なら入水したかった...

1-2 A問題 Anyway Takahashi

問題

整数$A,B,C,D$が与えられます。
以下の指示に従ってください。

一行目は$(A+B)×(C-D)$を出力し、二行目にはTakahashiを出力する。

制約

・$ -100 \leq A,B,C,D \leq 100$
・$A,B,C,D$は整数

解説

久し振りの「やるだけ」の問題です。
出力・入力や四則演算などの知識さえあれば解けます。
特に言うとすればタイプミスに気を付ける程度でしょう。

実装

A,B,C,D=map(int,input().split())
print((A+B)*(C-D))
print("Takahashi")

1-3 B問題 Rectangle Detection

問題

以下の方法で$10$個の文字列$S_1,S_2,...S_{10}$を生成します。

・まず$S_i(1 \leq i \leq 10)=..........$を生成する。
・次に下の条件を全て満たす整数$A,B,C,D$を生成する。

$1 \leq A \leq B \leq 10 , 1 \leq C \leq D \leq 10$

その後以下の条件を全て満たす整数の組$(i,j)$について$S_i$の$j$文字目を#に変換する。

$A \leq i \leq B , C \leq j \leq D$

この方法で生成された$10$個の文字列 $S_1,S_2,...S_{10}$が入力として与えられるので、生成した整数$A,B,C,D$を出力して下さい。

制約

・$|S_i|=10$
・$S_i$は上の方法で生成できる

解説

「$(i,j)$について$S_i$の$j$文字目を#に変換する」とあるので、#になっている点を見ればよいです。
その点全ての$x$軸、$y$軸(?)の最大値・最小値を求めることで$A,B,C,D$を出せます。
要は、長方形の頂点の座標を計算するということですね。

実装

S=[list(input()) for _ in range(10)]

xmx,xmn,ymx,ymn=0,10000,0,10000
for i in range(10):
  for j in range(10):
    if S[i][j]=="#":
      xmx=max(xmx,i)
      xmn=min(xmn,i)
      ymx=max(ymx,j)
      ymn=min(ymn,j)
print(xmn+1,xmx+1)
print(ymn+1,ymx+1)

それぞれの値の出力する順番と、1-indexedにすることに気を付けましょう。

1-4 C問題 Submask

問題

非負整数$N$が与えられるので、以下の条件を満たす非負整数$x$を昇順に全て入力してください。

全ての非負整数$k$について、次の条件を満たす。

$N$と$x$をそれぞれ二進数で表した時に、$x$の$k$桁目が$1$であるならば$N$の$k$桁目も必ず$1$である。

制約

・$N$は整数、$0 \leq N < 2^{60}$を満たす
・$N$を二進数で表した時$1$となる桁は$15$個以下

解説

例えば、$N=10_{(10)}=1010_{(2)}$の時、$x$を全て列挙すると

$0000_{(2)}=0_{(10)}$
$0010_{(2)}=2_{(10)}$
$1000_{(2)}=8_{(10)}$
$1010_{(2)}=10_{(10)}$

となります。$N$を二進数表記した時、$1$がある桁は$2$つなので$2^2=4$通りあります。
ということはbit全探索ですね。
制約にも、「$N$を二進数で表した時、$1$となる桁は$15$個以下」とあるので、$N$を二進数表記した時の$1$となる桁の数を$n$として、$O(2^n)$で間に合います。

$N$を二進数表記した時に$1$となる桁を求め、その桁について$0$か$1$かを全探索します。

実装

N=int(input())

one=[]
for i in range(60):
  if N>>i&1:
    one.append(i)
l=len(one)

for i in range(1<<l):
  now=0
  for j in range(l):
    if i>>j&1:
      now+=(1<<one[j])
  print(now)

$x$としてあり得る数は、必ず小さい物から順に出て来るので、わざわざ配列に格納してソートする必要はありません。

bit全探索は割と頻出するアルゴリズムです。
慣れていない方はこれを機にbit演算に慣れましょう。
こちらのけんちょんさんのサイトにとても詳しく載っています。

1-5 D問題 Do use hexagon grid

問題

無限に広い、六角形のグリッドがあります。
最初は全て白いです。
$N$個のマス$(X_1,Y_1),(X_2,Y_2),...(X_N,Y_N)$を黒く塗ります。
黒く塗った後、黒いマスの連結部分がいくつ存在するか求めて下さい。
又、マス$(i,j)$は次のマスと隣接します。

$(i-1,j-1)$
$(i-1,j)$
$(i,j-1)$
$(i,j+1)$
$(i+1,j)$
$(i+1,j+1)$

制約

・入力は全て整数
・$1 \leq N \leq 1000$
・$|X_i|,|Y_i| \leq 1000$
・$(X_i,Y_i)$は相異なる

解説

連結部分の個数を求める問題です。UnionFindを使うことで解けます。
勿論、DFSでも解けますが、私はUnionFindの方がやりやすい気がするので、UnionFindをお勧めします。
ここではUnionFindで実装します。

$2$つのマスの組を全探索し隣接しているか調べます。
隣接していればUnionFind上で連結させ、最後に連結部分の個数を出せばよいです。

実装(UnionFind以外)

N=int(input())
P=[tuple(map(int,input().split())) for _ in range(N)]

U=UnionFind()
for i in range(N):
  U.add(i)

OK={(-1,-1),(-1,0),(0,-1),(0,1),(1,0),(1,1)}
for i in range(N):
  ax,ay=P[i]
  for j in range(i+1,N):
    bx,by=P[j]
    if (ax-bx,ay-by) in OK:
      U.union(i,j)

for i in range(N):
  U.find(P[i])

seen=set()
ans=0
for i in range(N):
  par=U.parent[P[i]]
  if par in seen:
    continue
  seen.add(par)
  ans+=1

print(ans)

悲しい事実

残念なことに、PythonにUnionFindのライブラリが無い為、UnionFindを自分で用意するしかありません。 一応、私の使っているUnionFindのコードを添付します。 参考までに。

import sys
sys.setrecursionlimit(10**9)

class UnionFind:
  def __init__(self):
    self.parent={}; self.size={}
  
  def find(self,x): #一番上の親
    if self.parent[x]==x: return x
    else: self.parent[x]=self.find(self.parent[x]); return self.parent[x]
  
  def add(self,x): #頂点の登録
    self.parent.setdefault(x,x); self.size.setdefault(x,1)
  
  def issame(self,x,y):　#2頂点が連結しているか
    return self.find(x)==self.find(y)
  
  def union(self,x,y): #頂点の連結
    a,b=self.find(x),self.find(y)
    if a==b: return False
    if self.size[a]>self.size[b]: a,b=b,a
    self.parent[b]=a
    self.size[a]+=self.size[b]
    return True
  
  def size(self,x): #部分木の大きさ
    return self.size[x]
　
　def prt(self,x): #親
    return self.parent[x]
  
  def prtsize(self,x): #頂点の属するグループの要素数
    return self.size[self.find(x)] 

UnionFindを使う問題はグラフ問題に限らず多く出題されています。
UnionFindを実装していなかった方はこちらの私の記事を参考に実装してみても良いでしょう。
こちらの記事も参考になります。
UnionFindの分かりやすい説明

1-6 E問題 Last Rook

問題

これはインタラクティブな問題です。
縦横$N$マスのチェス盤と$N$個のルークの駒があります。
(左から$i$行目、上から$j$列目のマスを$(i,j)$と表します)
現在、$N-1$個のルークの駒がチェス盤に置かれており、次の条件を満たしています。

・$1$つの縦の列に、$2$個以上のルークが存在しない。
・$1$つの横の列に、$2$個以上のルークが存在しない。

次の質問をすることで、ルークを置けるマスを$1$つ出力して下さい。

・$1 \leq A \leq B \leq N, 1 \leq C \leq D \leq N$を満たす$A,B,C,D$を選ぶ。
・$A \leq i \leq B, C \leq j \leq D$を満たすマス$(i,j)$より成る長方形領域内にあるルークの個数を訊く。

尚、選んだ数を$A,B,C,D$として? A B C Dのように質問して下さい。
質問は$20$回までしか行えません。

制約

・$N$は整数、$2 \leq N \leq 10^3$

解説の前に

プログラムとジャッジプログラムが入出力で対話する形式の「インタラクティブな問題」です。
昔からAtCoderでは出題されており、最近でも稀に登場します。
ABC244-Cでも出題されました。

解説

問題はこう言い換えられます。

質問によって、指定した長方形の範囲の中に存在するルークの数を知ることが出来ます。
$20$回以下の質問を元に、ルークが存在しない行・列を出力して下さい。

質問回数の制限が無ければ、行・列の特定にそれぞれ$N$回の質問をしても解けますし楽ですが、質問回数の制限から見て到底無理そうです。

チェス盤の一辺が$4$で、ルークの位置が次のようである場合を考えてみましょう。

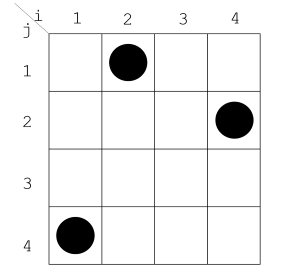
この時、左から$1$列にはルークは$1$個、左から$2$列には$2$個あるのに対し、左から$3$列には$3-1=2$個、左から$4$列には$4-1=3$個存在します。
$1,2,4$列目には$1$個ずつルークがあるのに対し$3$列目は$0$個なので、$3$を節目に、iと左からi列までに存在するルークの数が等しくなくなります。

つまり、次のような問題に言い換えられます。

iと左からi列までに存在するルークの数が等しくなくなる境目を求めて下さい。

これは二分探索法を使って解けますね。
ルークが存在しない列の例を挙げましたが、ルークが存在しない行を求める場合も同様に求められます。
左端を0、右端をNとして、「i = 左からi列までに存在するルークの数」という判定問題を質問から解けばよいです。
判定問題がfalseとなる最小のiが求めるべき値です。

$1 \leq N \leq 10^3$ですので、それぞれ$10$回以内で列と行を特定できます。($10^3 \leq 2^{10}$)よって、合計$20$回以内の質問で特定できますね。これで、回数の制限に引っ掛からずに済みます。
左端を1と設定してしまうと、最左列か最上段に求めるべきマスが存在する時に誤った解答をしてしまうので注意しましょう。

実装

N=int(input())

x,y=0,0

left,right=0,N
while left+1<right:
  mid=(left+right)//2
  print("?",1,mid,1,N)
  T=int(input())
  if T==mid:
    left=mid
  else:
    right=mid
x=right

left,right=0,N
while left+1<right:
  mid=(left+right)//2
  print("?",1,N,1,mid)
  T=int(input())
  if T==mid:
    left=mid
  else:
    right=mid
y=right

print("!",x,y)
exit()

Diffは1050と、割と高めですが、やることは年齢当てゲーム(対数回数の質問で年齢を当てるアレです)と同じですね。

2 さいごに

最後までお読み頂きありがとうございます。
今回はアルゴリズムやプログラミングの基礎的な問題がメインの回でしたね。
Twitterを見ていると、全体的に考察が必要な問題が少なくつまらなかったという声も見受けられました。
私は記事の編集が楽で嬉しかったですが
以上です。
お読み頂きありがとうございました。
よい競プロライフを!!
いいねお願いします...(切実)

-1 おまけ(ヲイ) C++での実装

C++での実装の需要が高い気がしましたのでC++でも書きました。
今後はもっとC++Userさん向けにしていきたいです。
今回はごめんなさい。

A問題

#include <bits/stdc++.h>
using namespace std;

int main(){
  int A,B,C,D; cin>>A>>B>>C>>D;
  cout<<(A+B)*(C-D)<<endl;
  cout<<"Takahashi"<<endl;
}

B問題

#include <bits/stdc++.h>
using namespace std;

#define rep(i,N,M) for(int i=N; i<M; i++)

int main(){
  vector<string> S(10);
  rep(i,0,10){
    cin>>S[i];
  }
  
  int xmn=1000,xmx=0,ymn=1000,ymx=0;
  rep(i,0,10){
    rep(j,0,10)}
      if(S[i][j]=='#'){
        xmn=min(xmn,i+1);
        xmx=max(xmx,i+1);
        ymn=min(ymn,j+1);
        ymx=max(ymx,j+1);
      }
    }
  }
  
  cout<<xmn<<" "<<xmx<<endl;
  cout<<ymn<<" "<<ymx<<endl;
}

C問題

#include <bits/stdc++.h>
using namespace std;
using ll=long long;
#define rep(i,N,M) for(int i=N; i<M; i++)

int main(){
  ll N; cin>>N;
  
  vector<int> one;
  rep(i,0,60){
    if(N>>i&1){
      one.push_back(i);
    }
  }
  
  int l=one.size();
  
  rep(i,0,1<<l){
    ll now=0;
    rep(j,0,l){
      if(i>>j&1){
        now+=1LL<<one[j];
      }
    }
    cout<<now<<endl;
  }
}

D問題

#include <bits/stdc++.h>
#include <atcoder/all>
using namespace std;
using namespace atcoder;

int main(){
  int N; cin>>N;
  vector<vector<int>> P(N,vector<int>(2));
  rep(i,0,N){
    int a,b; cin>>a>>b; a--; b--;
    P[i][0]=a; P[i][1]=b;
  }
  
  dsu U(N);
  rep(i,0,N){
    int ax=P[i][0],ay=P[i][1];
    rep(j,i+1,N){
      int bx=P[j][0],by=P[j][1];
      int n=ax-bx,m=ay-by;
      bool flag=false;
      if(n==-1){
        if(m==-1 or m==0){
          flag=true;
        }
      }else if(n==0){
        if(m==-1 or m==1){
          flag=true;
        }
      }else if(n==1){
        if(m==0 or m==1){
          flag=true;
        }
      }
      if(flag){
        U.merge(i,j);
      }
    }
  }
  
  cout<<U.groups().size()<<endl;
}

ACL便利やな...

E問題

#include <bits/stdc++.h>
using namespace std;

int main(){
  int N; cin>>N;
  int x,y;
  
  int left=0,right=N;
  while(left+1<right){
    int mid=(left+right)/2;
    cout<<"? "<<1<<" "<<mid<<" "<<1<<" "<<N<<endl;
    int T;
    cin>>T;
    if(T==mid){
      left=mid;
    }else{
      right=mid;
    }
  }
  x=right;
  
  left=0; right=N;
  while(left+1<right){
    int mid=(left+right)/2;
    cout<<"? "<<1<<" "<<N<<" "<<1<<" "<<mid<<endl;
    int T;
    cin>>T;
    if(T==mid){
      left=mid;
    }else{
      right=mid;
    }
  }
  y=right;
  
  cout<<"! "<<x<<" "<<y<<endl;
  return 0;
}

C++はあまり上手くないので許してください..
一応ACするかは確認してますが無駄な挙動があるかも知れません。