はじめに
オペレーションズ・リサーチの分野はデータサイエンスの領域ではAIや機械学習ほどメジャーではないかもしれない。ただ、広くは数理最適化問題を扱い、最適なシステムの運用を研究するものであるので、筆者はその有用性を広めてこの研究分野を活発にし発展に貢献したい。特に今回はデータ包絡分析法(Data Envelopment Analysis)について取り上げた。
※この記事は専門分野外の方に対してわかりやすい説明を意図している
目次
1. DEAとは
一言でいうと、入出力の関係をもつデータの効率性をノンパラメトリックに評価する手法。入力は少なく、出力が大きい方が望ましいという関係を持つ。なんらかのデータを評価する場合によく用いられる。例えば銀行の各支店、賃貸物件、ビルエネルギー、営業マンなどなど。
1.1. 例を用いて考える
あるコンビニエンスストアを経営しているとする。5店舗を管理しているが、どうやら各店舗は異なる状況にあるようだ。経営者は店舗の運用を最適化することで、利益(売上ー運用コスト)を伸ばしたいと考えている。
| 店舗 | 従業員数 | 設備運用費 | 売上 |
|---|---|---|---|
| a | 50 | 110 | 300 |
| b | 70 | 80 | 250 |
| c | 30 | 120 | 270 |
| d | 45 | 90 | 200 |
| e | 50 | 210 | 400 |
経営者の目線に立って考えると、次のことをしたくなる。
- コスパの良い店舗を探す
- コスパの悪い店舗を探し、コスパの良い店舗になるように改善を実行する
この場合、コスパとは何でありどうやって測るのか?ということが問題となる。
1.2. コスパとは効率値である
およそ感覚的にはこのような感じで、入力(従業員と設備)に対する出力(売上)の割合を効率値(コスパ)であると考えることができる。この入力、出力をもつ意思決定器をDMU(Decision Maiking Unit)という。つまりあるDMUとはある一つの店舗のことだ。
$$ 効率性 = \frac {売上}{従業員数 + 設備費}$$
この概念を取り入れると先ほどの目標は、次のように言い換えられる。要はなるべく少ない従業員数と設備費で最大限の売上を出したいのだ。(従業員の幸福度は考えないものとする)
- 効率値の高い($=1$)店舗を探す
- 効率値の低い店舗を探し、入出力を増加減して効率値を上げる($=1$とする)
1.3. 可視化
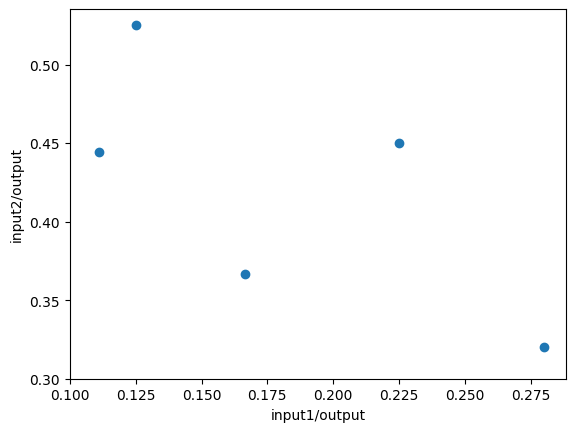
2入力1出力の場合は二次元で可視化できるので視覚的に理解できる。
出力あたりの入力は少ない方がいいので、左下ほど良い状態であり、右上ほど非効率的な状態であるようにみえる。
DEAを適用しよう
Pythonライブラリがあるので簡単である。(Pyfrontier)
from Pyfrontier.frontier_model import EnvelopDEA
import pandas as pd
df = pd.DataFrame(
{
"employee": [50, 70, 30, 45, 50],
"cost": [110, 80, 120, 90, 210],
"profit": [300, 250, 270, 200, 400]}
)
dea = EnvelopDEA("CRS", "in")
dea.fit(df[["employee", "cost"]].to_numpy(), df[["profit"]].to_numpy())
dea.results
| 店舗 | 従業員数 | 設備運用費 | 売上 | 効率値 |
|---|---|---|---|---|
| a | 50 | 110 | 300 | 1 |
| b | 70 | 80 | 250 | 1 |
| c | 30 | 120 | 270 | 1 |
| d | 45 | 90 | 200 | 0.802168 |
| e | 50 | 210 | 400 | 0.888889 |
たとえば、ここでdの結果詳細は、
EnvelopResult(score=0.802168, id=3, dmu=DMU(input=array([45, 90]), output=array([200]), id=3), weight=[0.585366, 0.097561, 0.0, 0.0, 0.0], x_slack=[0.0, 0.0], y_slack=[41.54472])
となり、dの目標値は重みを用いて$DMU1 \times 0.585366 + DMU1 \times 0.097561$より次となる。
| 店舗 | 従業員数 | 設備運用費 | 売上 | 効率値 |
|---|---|---|---|---|
| d | 50 | 110 | 300 | 0.802168 |
| 理想d | 36.09 | 72.20 | 300 | 1 |
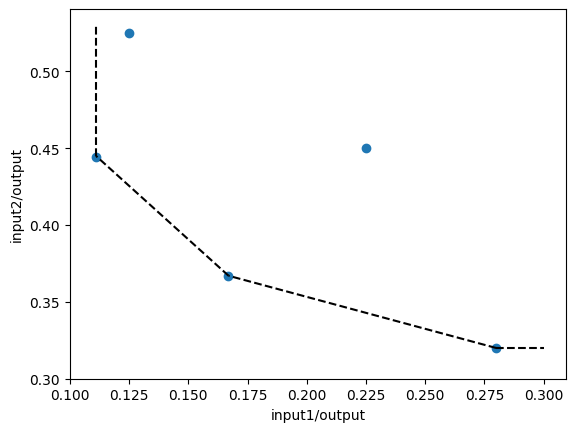
これより、売上を変えずに、従業員数を14人と設備運用費を38ほど減らせばデータ上は効率的な状態になる。このようにDEAは、データ上から効率の悪いデータを見つけて、改善量を客観的に与えることができる。
もちろん利点だけでなく課題もある。例えば、極端に効率的なデータがある場合、非効率なデータがフロンティアに到達するまでの改善量が大きくなり実現不可能になってしまうなどである。そのほかにも課題はあるが、それぞれは様々なモデルが提案され、日々改善されつづけている。
中央にあるdはこの改善によって点線上のフロンティアに移動する。
備考1: その他モデル
この例では入力値を少なくすることで改善する(入力指向)、という前提で考えた。出力値を大きくすることで改善する(出力指向)、という前提もある。基本的にはどちらかの方針をとるが、どちらかを限定しないモデル(slack-based model)もある。対応したい状況やとれる手段によってモデルを選ぶ必要がある。
備考2: 定式化(入力指向DEA)
\theta^* = \min \theta, subject \ to \\
\sum_{j=1}^{n} \lambda_j x_{i, j} \leq \theta x_{i, o}, i=1,2, \dots, m; \\
\sum_{j=1}^{n} \lambda_j y_{r, j} \geq y_{r, o}, r=1,2, \dots, s; \\\\
\lambda_j \geq 0, j=1,2, \dots, n.
$x_{i, o}$、$y_{r, o}$は$o$番目のデータのi, r番目の入力、出力で、$\theta$は効率値です。これはつまり、自分以外のデータにもっとも都合が良いように自分を評価した場合の値です。単純な線形計画問題を解けば算出できます。
2. 応用事例
2.1. ホテルのエネルギー効率についての応用例。(論文)
- サンプルデータ
| 物件 | 従業員数 | エネルギー消費量(単位面積あたり) | 年間収入 | 滞在率 | ゲスト数 |
|---|---|---|---|---|---|
| 物件1 | 50 | 200 | 200 | 0.8 | 200 |
| 物件2 | 300 | 500 | 1000 | 0.7 | 800 |
| ... | ... | ... | ... | ... | ... |
この場合、以下によって効率値を算出する
- 入力
- 従業員数
- エネルギー消費量
- 出力
- 年間収入
- 滞在率
- ゲスト数
2.2. 空調器の運用効率についての応用。(論文)
DEAの入出力は、単に大きい方がいい値(出力)と小さい方がいい値(入力)を評価することもできる。必ずしも数学的な入出力の関係性を必要とはしないので、こういった応用も可能である。
- サンプルデータ
| 日 | 室内機Aの運転時間 | 室内機Bの運転時間 | 室内機Cの運転時間 |
|---|---|---|---|
| 7/26 | 100 | 200 | 200 |
| 8/1 | 150 | 300 | 150 |
| ... | ... | ... | ... |
- 入力
- 室内機Aの運転時間
- 室内機Bの運転時間
- 室内機Cの運転時間
- 出力
- $1$(定数)
2.3. その他応用
日本オペレーションズ・リサーチ学会 評価のOR研究部会ではいくつもの適用事例が紹介されている。
4. 様々なモデル
より実用的な問題に対応するために、以下のような手法が提案されている。
これらは上記(ライブラリ)に機能としてあるが、日本語のドキュメントはないので機会があれば解説する。
- コントロールできない要因
- 改善のために操作しない変数を設定する(外気温など人類がコントロールできないもの)
- 指向を選ばないモデル
- 入力を減らし出力を増やすことが可能だが、逆に不可能になる操作がある
- 改善する変数に関係性を仮定する
- たとえば従業員数の方が設備運用費よりも二倍重要である、ということ
- 効率値1のDMUを評価するモデル
- 効率的DMU自体を評価する際(効率的すぎるものを除外)につかう
5. おわりに
DEAは単純ではあるが効果的に作用する問題形式があるので、機械学習やAI等の一モデルと捉えて理解しておくと、使い所をみつけて思わぬところで応用ができるかもしれない。経営の科学として限定的な領域で使われていることがおおく、Pythonライブラリも近年まで有用なものがない状態(ExcelやR、商用ソフトウェアなどが使われていた)であったので、この状況を変えてより多くの人が分析する際の選択肢として選ぶことができるようになれば、と思い執筆に至る。