トポロジカルソートって何?実装は!?調べてみました!

タイトルはふざけました。ごめんなさい。
近畿大学 Advent Calendar 2019　18日目の記事です。
#0. はじめに
突然ですが、朝起きてからどんな順番で着替えますか?
シャツを着てからズボンを穿く人、またはその逆は居ても、ベルトを締めてからズボンを穿く人は居ませんよね。つまり着替える時、それぞれのタスクには以下のような依存関係があります。

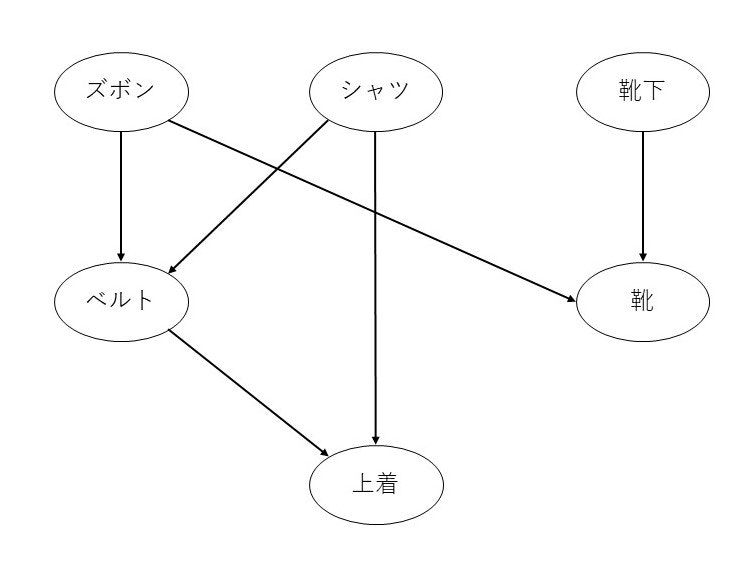
図1 着替える時のタスクの依存関係を、有向グラフとして表したもの

このようにタスク間に依存関係がある場合、どんな順番でタスクをこなせば良いかを決めるのに役立つアルゴリズムがトポロジカルソートです。

本記事では

• トポロジカルソートが何となく分かる
• トポロジカルソートを実装できる

を目指していきたいと思います。

対象読者は

• グラフについて基礎的な用語を知っている
• 幅優先探索を実装できる

ぐらいの方を想定しています。
#1. トポロジカルソート
##1.1 トポロジカルソートとは
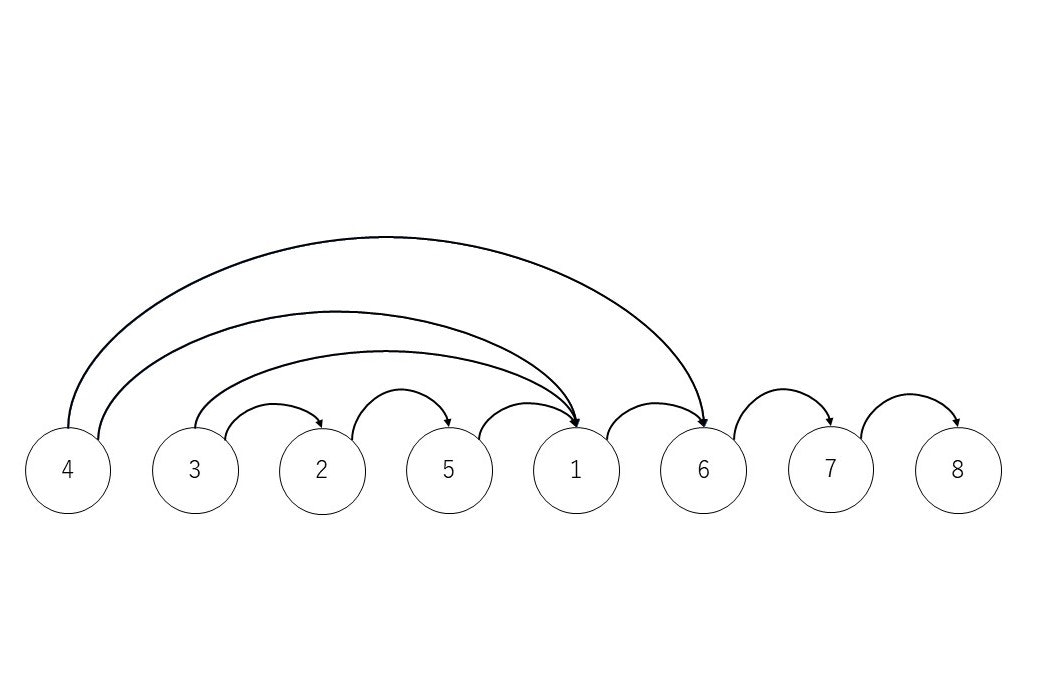
以下のような有向グラフが与えられたとします。

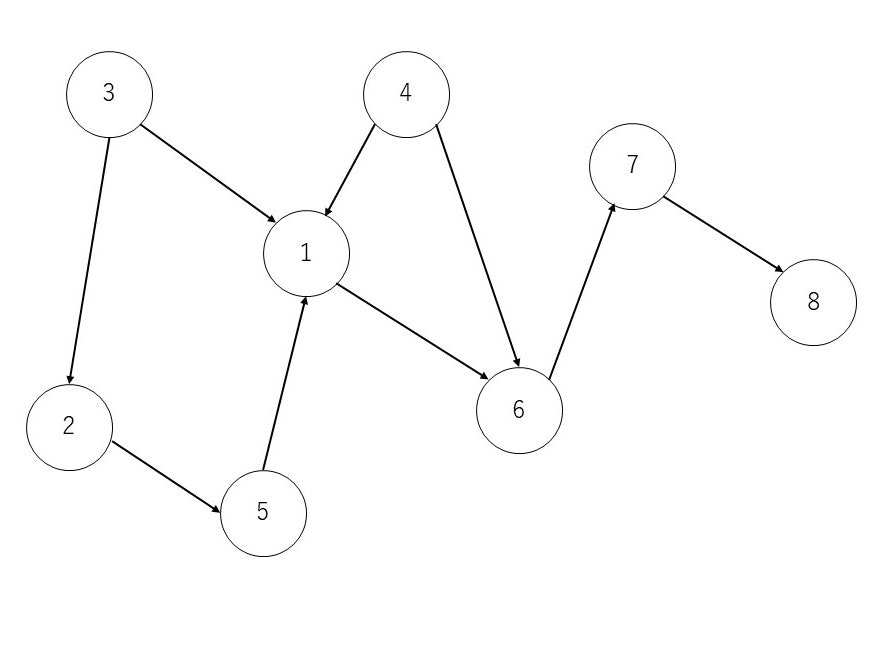
図2 有向グラフ

この有向グラフで、頂点$u$から頂点$v$に到達できることを、$R(u, v)$と書くとします。

例えば図では$R(3, 1)$や$R(1, 7)$などが成り立っていますが、$R(1, 3)$や$R(5, 4)$は成り立ちません。

トポロジカルソートとは、すべての頂点$u, v$について
$u \neq v$ かつ $R(u, v)$ ならば $u$ が $v$ よりも先に現れるように頂点を一列に並べることです。

図3 図2をトポロジカルソートした例その1

もしこの有向グラフがタスクの依存関係などを表していた場合、左からその頂点に対応するタスクを処理すれば、依存関係を守ったままタスクを全て処理することが出来ます。

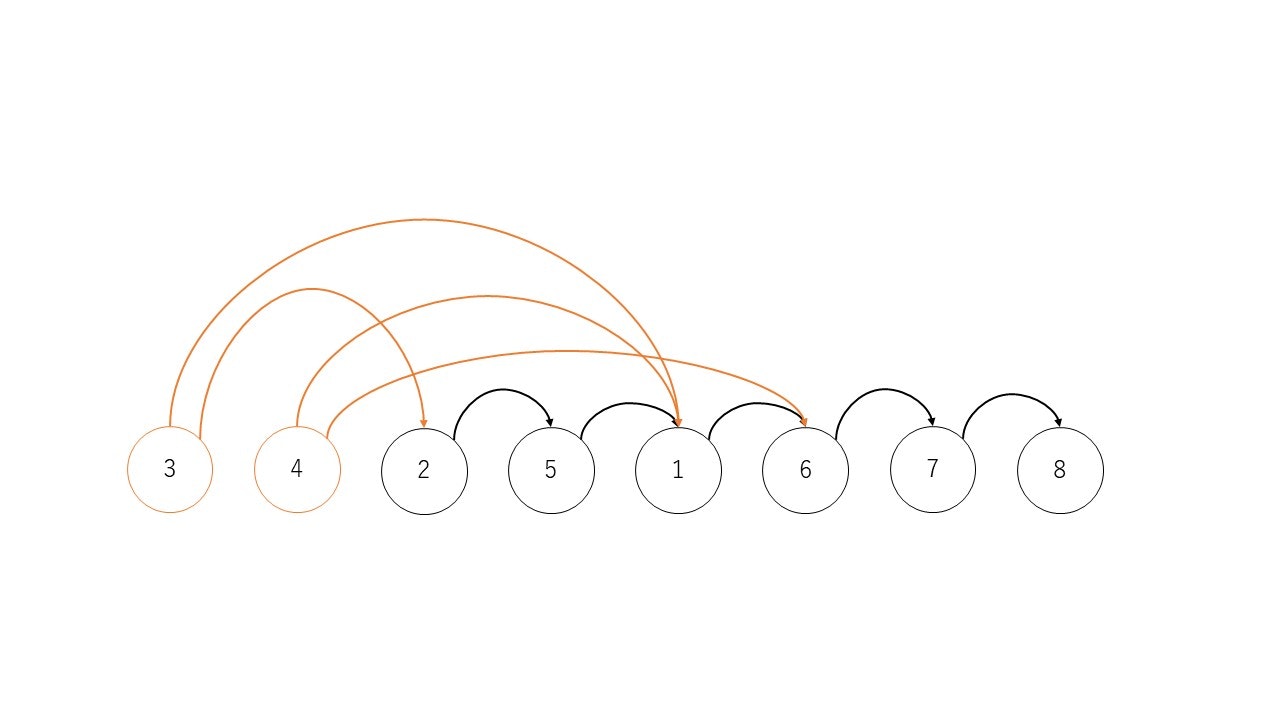
一般に、トポロジカルソートによる並び替えは一意的ではありません。例えば図3の他に以下のような並び替えもトポロジカルソートの条件を満たします。

図4 図2をトポロジカルソートした例その2。並び替わった頂点とその辺をオレンジで示した。

##1.2 トポロジカルソートできる条件
どんな有向グラフでもトポロジカルソートできる訳ではありません。

すべての頂点$u, v$について $R(u, v)$ かつ $R(v, u)$ ならば $u = v$ が成り立つ、かつその時に限り、その有向グラフをトポロジカルソートすることが出来ます。(つまり、ある頂点から出発して、その頂点に戻ってくるような路がない)

この条件を満たす有向グラフを

有向非巡回グラフ（directed acyclic graph, DAG）

と呼びます。

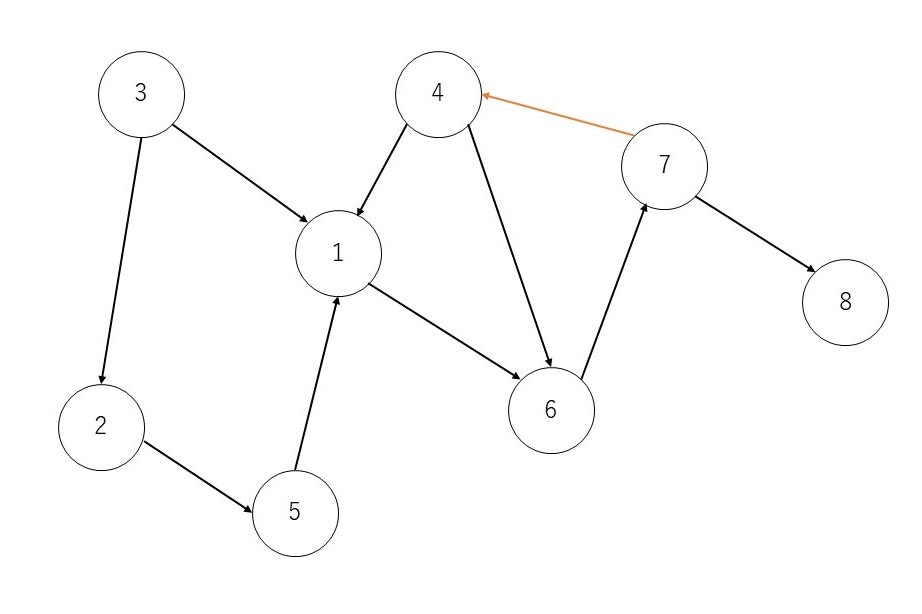
図2のグラフはDAGでしたが、例えば頂点7から頂点4への辺をグラフに追加すると、
$R(4, 1)$ かつ $R(1, 4)$などが成り立つようになり、DAGでは無くなります。
よってトポロジカルソートができなくなります。

図5 図2に辺を追加し、DAGでは無くなったグラフ。

##1.3 トポロジカルソートの実装例(C++)
トポロジカルソートを実装するだけの問題がAizu Online Judge(AOJ)にあるので、それを解くコードを書いてみましょう。

Topological Sort - Aizu Online Judge

まず問題に書いてある形式で有向グラフが与えられるので、それを受け取ります。
受け取りながら、頂点の入次数も記録しておきましょう(後で入次数を使うので)。

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

int main(void) {
    // 頂点数と辺の本数
    int V, E;
    cin >> V >> E;

    // 隣接リストにより表現されるグラフ
    vector<vector<int>> G(V);
    // 頂点の入次数を記録する配列
    vector<int> indegree(V);
    for (int i = 0; i < E; i++) {
        int u, v;
        cin >> u >> v;
        G[u].push_back(v);
        indegree[v] += 1;
    }

    return 0;
}

さてどうやって与えられたDAGをトポロジカルソートするかですが

1. 入次数0の頂点$v$を発見する。
2. 頂点$v$を配列の末尾に追加する。
3. 有向グラフから頂点$v$と、その頂点から出ている辺をすべて削除する

これを繰り返し、すべての頂点を取り除いた後に得られる配列を出力すれば
それが与えられたDAGのトポロジカルソートになっています。

操作1へ戻るたびに全ての頂点の入次数を1つずつ調べるなど、愚直に実装してしまうと計算量が大きくなりますが
操作3によって入次数が変化する頂点は、削除した頂点と隣接している頂点だけということに着目すれば、
全ての頂点の入次数を調べるのは最初だけで良いことが分かります。
発見した入次数0の頂点はキューやスタックに保存しておくと、後で高速に取り出せます。

では、トポロジカルソートする関数を実装してみましょう。

// グラフ、頂点の入次数、頂点数を受け取り、そのトポロジカルソートを記録した配列を返す関数
vector<int> topological_sort(vector<vector<int>> &G, vector<int> &indegree, int V) {
    // トポロジカルソートを記録する配列
    vector<int> sorted_vertices;

    // 入次数が0の頂点を発見したら、処理待ち頂点としてキューに追加する
    queue<int> que;
    for (int i = 0; i < V; i++) {
        if (indegree[i] == 0) {
            que.push(i);
        }
    }

    // キューが空になるまで、操作1~3を繰り返す
    while (que.empty() == false) {
        // キューの先頭の頂点を取り出す
        int v = que.front();
        que.pop();

        // その頂点と隣接している頂点の入次数を減らし、0になればキューに追加
        for (int i = 0; i < G[v].size(); i++) {
            int u = G[v][i];
            indegree[u] -= 1;
            if (indegree[u] == 0) que.push(u);
        }
        // 頂点vを配列の末尾に追加する 
        sorted_vertices.push_back(v);
    }

    // トポロジカルソートを返す
    return sorted_vertices;
}

後はこの関数を呼び出し、返ってきた配列を前から出力するだけです。

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

// グラフ、頂点の入次数、頂点数を受け取り、そのトポロジカルソートを記録した配列を返す関数
vector<int> topological_sort(vector<vector<int>> &G, vector<int> &indegree, int V) {
    // トポロジカルソートを記録する配列
    vector<int> sorted_vertices;

    // 入次数が0の頂点を発見したら、処理待ち頂点としてキューに追加する
    queue<int> que;
    for (int i = 0; i < V; i++) {
        if (indegree[i] == 0) {
            que.push(i);
        }
    }

    // キューが空になるまで、操作1~3を繰り返す
    while (que.empty() == false) {
        // キューの先頭の頂点を取り出す
        int v = que.front();
        que.pop();

        // その頂点と隣接している頂点の入次数を減らし、0になればキューに追加
        for (int i = 0; i < G[v].size(); i++) {
            int u = G[v][i];
            indegree[u] -= 1;
            if (indegree[u] == 0) que.push(u);
        }
        // 頂点vを配列の末尾に追加する 
        sorted_vertices.push_back(v);
    }

    // トポロジカルソートを返す
    return sorted_vertices;
}

int main(void) {
    // 頂点数と辺の本数
    int V, E;
    cin >> V >> E;

    // 隣接リストにより表現されるグラフ
    vector<vector<int>> G(V);
    // 頂点の入次数を記録する配列
    vector<int> indegree(V);
    for (int i = 0; i < E; i++) {
        int u, v;
        cin >> u >> v;
        G[u].push_back(v);
        indegree[v] += 1;
    }

    // トポロジカルソートする
    vector<int> sorted_vertices = topological_sort(G, indegree, V);

    // トポロジカルソートを出力
    for (int i = 0; i < sorted_vertices.size(); i++) {
        cout << sorted_vertices[i] << endl;
    }

    return 0;
}

頂点の数を$|V|$、辺の本数を$|E|$とした時
この実装による計算量は$O(|V|+|E|)$です。

さて、このプログラムを上記の問題へ提出してみると...

AC(Accepted)! 全てのデータセットに正しい回答をすることができました。
#2. おわりに
いかがでしたか？問題にACしたので上記のアルゴリズムの正当性は証明されました！
本当はアルゴリズムの正当性の証明もしたいのですが、僕の数学力不足のせいで証明が書けません。ごめんなさい。

DAGの条件から、頂点を1つ選んで入次数0でなければ辺を逆向きにたどって行くことを繰り返すと有限ステップで入次数0の頂点が見つかる事と、
グラフの頂点数に関する帰納法から証明できるのかな...?とか考えましたが、どう書いて良いのか分かりません。

もし読んでくださっている方の中に、証明できる方が居れば教えてください m(_ _)m

最後まで読んでいただいて有難うございました。

#3. 参考文献

• T. コルメン, C. ライザーソン, R. リベスト, C. シュタイン(2013)『アルゴリズムイントロダクション』(浅野哲夫, 岩野和生, 梅尾博司, 山下雅史, 和田幸一訳)近代科学社
• 渡部有隆(2015)『プログラミングコンテスト攻略のためのアルゴリズムとデータ構造』マイナビ出版
• 秋葉拓哉, 岩田陽一, 北川宜稔(2012)『プログラミングコンテストチャレンジブック　第2版』マイナビ出版