はじめに
「たたみこみ」とは「合成積」のことです(と言われるとよけい分からない)。
・和室とは関係ありません
・柔道の寝技でもありません。
東北工業大学の中川先生は、「人生、たたみこみ」と書いておられますが、私は正直、そこまで達観した「たたみこみ観」は持っていないので、実践的な「たたみこみ」の説明を書いてみます。
なお、CNN(たたみこみニューラルネットワーク)については、本稿では触れません。
1.なぜ「たたみこみ」が必要なのか
「たたみこみ」の例としては、音響のエコー(反射)が良く知られています。
下図のように人がいて、1カ所に反射物があったとします。

人と反射物の距離がLで音速がVcだとすると、人が発生した音声は、反射物で反射し、2L/Vc 秒後に人に戻ってきます(2は往復なので)。
また、図2のように2カ所に反射物があり、人からの距離が2つの反射物までの距離が、それぞれLa,Lbだとしますと、それぞれの反射物からの音は、2La/Vc、2Lb/Vc 秒後に返ってきます。
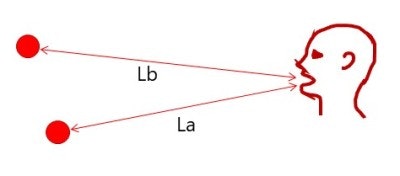
それぞれから返ってくる音の大きさが同じで、波形に崩れがない(線形)とします。
このとき、2つの反射物からの音は、時間をずらして加算されます。
これをMATLAB的に書くと、
wave=load('wave.dat'); %波形データを読み込む
wavelen=length(wave); %波形データの点数
fs=10e3; % サンプリング周波数[Hz]
Vc=340; % 音速[m/sec]
La=4; % A点までの距離[m]
Lb=6; % B点までの距離[m]
Pa=round(2*La/Vc*fs); % A点までの往復の時間をサンプリング点数に換算
Pb=round(2*Lb/Vc*fs); % B点までの往復の時間をサンプリング点数に換算
WaveAll=zeros(1,600); % 合成波形を収納するためのゼロ配列
figure(1);
subplot(3,1,1);
plot(WaveAll);
text(20,0.5,'ゼロ配列');
WaveAll(Pa:(Pa+wavelen-1))=WaveAll(Pa:(Pa+wavelen-1))+wave;
subplot(3,1,2);
plot(WaveAll);
text(20,0.5,'A点の反射を加える');
WaveAll(Pb:(Pb+wavelen-1))=WaveAll(Pb:(Pb+wavelen-1))+wave;
subplot(3,1,3);
plot(WaveAll);
text(20,0.5,'さらにB点の反射を加える');
実行すると、下記のようなグラフが表示されます。
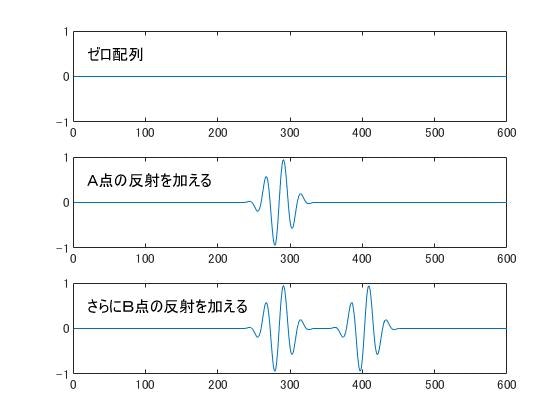
また、A点からの距離と、B点からの距離が近い場合は、波形が重なりますが、重なったところは両者の波形が加算された形になります。
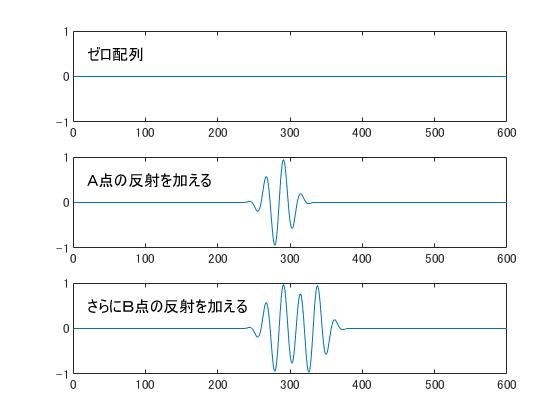
ところで、上で説明した演算は、けっこう面倒くさいものがあります。例えて言うなら、
y = ( 2 * a ) + ( 4.5 * a ) + ( 11 * a )
でaの値が与えられたときに、カッコの中から計算しちゃうような面倒くささがあります。
y = ( 2 + 4.5 + 11 ) * a
で計算すべきでしょう。
たたみこみ演算は、これに近い感じです(あくまでも「感じ」ですが)。
2.MATLABの「たたみこみ関数」convを使う
前章の2点からの反射の例では、波形そのものは同じで、返ってくる時間だけが異なっていました(反射信号の振幅も同じ)。
そこで、伝搬時間Pa, Pb(正確には伝搬時間をサンプリング周波数で割ったもの)と振幅の1だけを用いて、これら(遅延と振幅)を表現するインパルス列を作成します。
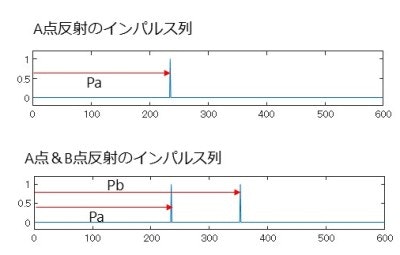
このインパルス列と信号波形の畳み込みを行ないます。
WaveOut = conv ( WaveIn , Inp ) ;
というような使い方で、スクリプトは、例えば、
wave=load('wave.dat'); %波形データを読み込む
fs=10e3; %サンプリング周波数[Hz]
Vc=340; %音速[m/sec]
La=4; %A点までの距離[m]
Lb=6; %B点までの距離[m]
Pa=round(2*La/Vc*fs); %A点までの往復の時間をサンプリング点数に換算
Pb=round(2*Lb/Vc*fs); %A点までの往復の時間をサンプリング点数に換算
WaveAll=zeros(1,600); %合成波形を収納するためのゼロ配列
figure(2);
WaveAll(Pa)=1;
subplot(4,1,1);
plot(WaveAll);
ylim([-0.2 1.2]);
text(20,0.5,'A点反射のインパルス列');
WaveAllA=conv(wave,WaveAll); %たたみこみ
subplot(4,1,2);
plot(WaveAllA);
xlim([0 600]);
text(20,0.5,'A点の反射のみ');
WaveAll(Pb)=1;
subplot(4,1,3);
plot(WaveAll);
ylim([-0.2 1.2]);
text(20,0.5,'A点B点反射のインパルス列');
WaveAll=conv(wave,WaveAll); %たたみこみ
subplot(4,1,4);
plot(WaveAll);
xlim([0 600]);
text(20,0.5,'A点、B点の反射');
実行すると下のようなグラフが出ます。
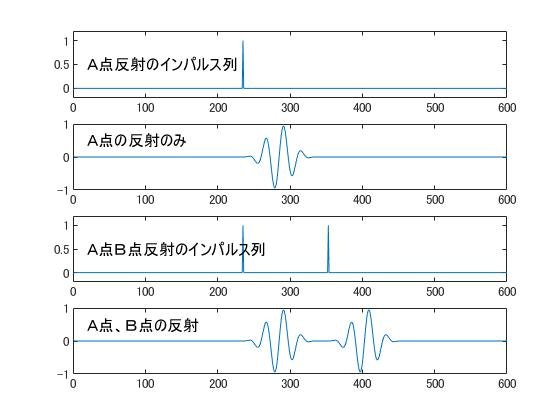
また、A点からの反射がB点からの2倍という場合は、インパルスの振幅を変えることで対応できます。
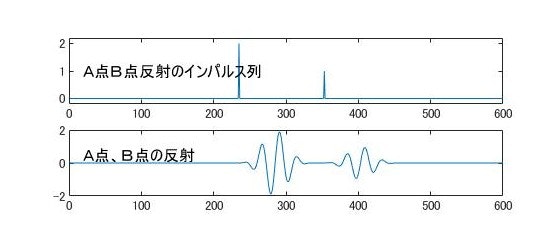
ここで、インパルス列とのたたみこみということで、説明しましたが、離散時間系においては、どのような波形(関数)もインパルスの組み合わせです。
よって、よく出てくる離散値のたたみこみの式、
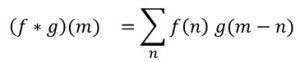
と同じことになります。
ということで、「たたみこみ」が何か、どうやるかのざっくりとした説明を終わります。
3.多数点からの反射をいかに計算するか
前章までで、シンプルな解説は終わったので、ここからは書きたいように書いてみましょう。
反射物として板みたいなものを考えます。板はXY平面上にあるとします。
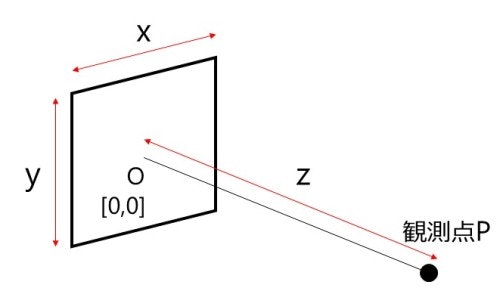
板の大きさ、観測点の位置関係は、次のとおりとします。
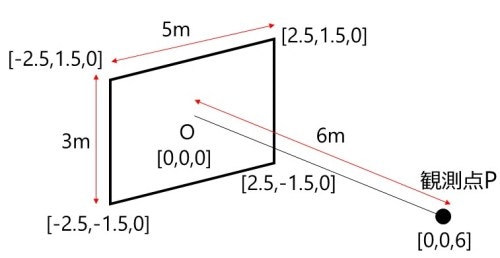
こういった場合には、セオリーとして、まず反射板をメッシュに切ります(シミュレーションの基本?)。
信号の波長とか演算精度と相談ですが、ここは0.1m格子でメッシュを切ってみましょう。
meshgridという関数が便利です。
x=-2.5:0.1:2.5;% X方向メッシュ設定
y=-1.5:0.1:1.5;% Y方向メッシュ設定
[X,Y]=meshgrid(x,y);% メッシュ生成
これで、メッシュ各点のX座標、Y座標の2次元配列ができました。
メッシュ各点から観測点Pまでの距離を求めます。
abs関数を用います。
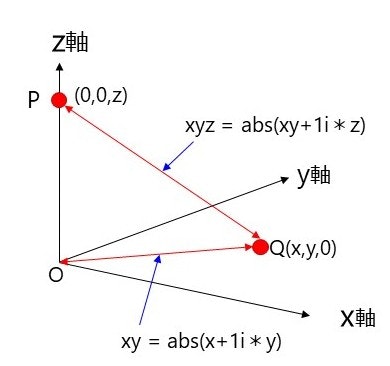
P=6; %観測点のZ座標[m]
Lxyz=abs(abs(X+1i*Y)+1i*P);
%%% 距離をサンプリング点に換算する
fs=10e3; %サンプリング周波数[Hz]
Vc=340; %音速[m/sec]
Pxyz=round(2*Lxyz/Vc*fs); % 2は往復
abs関数は絶対値計算と、複素数の大きさ計算に使えます。pythonなどでも使えるようですが。
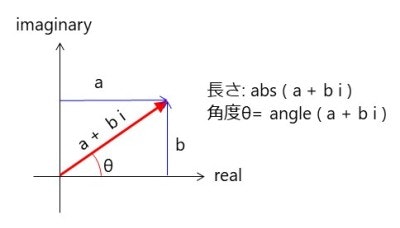
これで、たたみこみの元になる時間遅延データが完成しました。
問題はこの後、インパルス列をどうやって生成するかです。
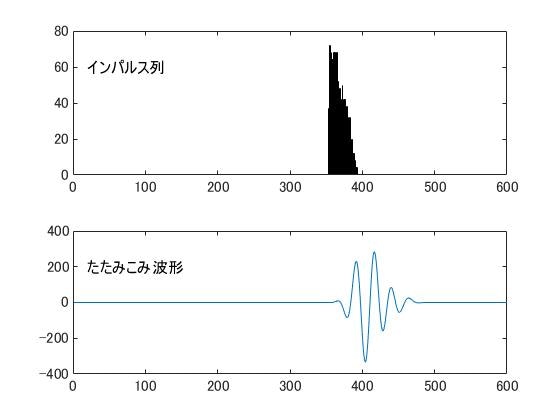
forループを回して「集計」するのが一般的かと思いますが、ここはヒストグラム(正しくはhistcounts)を使います。入力の振幅が揃っていないと使えないとか制約はありますが、個人的には「推し」です。
Pedges=0:600; %ヒストグラムの境界の位置
[N,edges]=histcounts(Pxyz,Pedges);
subplot(2,1,1);
histogram(Pxyz,Pedges);
xlim([0 600]);
text(20,60,'インパルス列');
WaveAll=conv(wave,N); %たたみこみ
subplot(2,1,2);
plot(WaveAll);
xlim([0 600]);
text(20,200,'たたみこみ波形');
下図のようなグラフが表示されます。
終わりに
「たまにはマジメなことを書くか」と言っておられる人もいたので、私もマジメに書いてみましたが、いかがでしたでしょうか。
ということで、終わります。
お疲れさまでした。