四角形同士の重なり判定

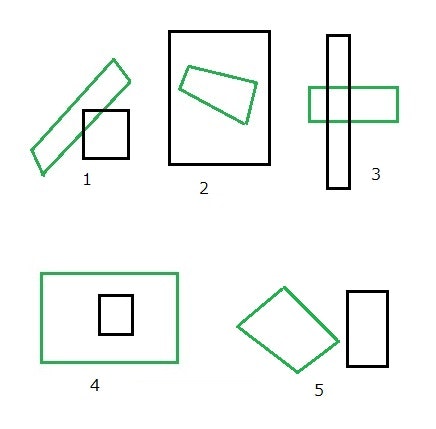
GUIアプリを作っている際に、ドラッグで選択した範囲（つまり直角四角形、今回作ったプログラムは直角四角形の性質は利用せず四角形一般で考えています）内に、ある四角形が重なっているかどうかを調べる必要がありました。少しややこしいのは、アプリの目的上、内包関係にある場合について、片方のみをTrueとしたいのです。

四角形が緑、選択範囲が黒です。上の図の5つの関係のうち上3つになっていればTrue、下のような四角形の内側でのみ選択範囲を指定している場合(4)や、そもそも重なっていない場合(5)にはFalseを返す関数が欲しいわけです。
そしてなるべく外部ライブラリに頼りたくない。
　
　
点と図形の内外判定の問題は「Point in Polygon」と呼ばれています。
https://en.wikipedia.org/wiki/Point_in_polygon

ググったところ、ここで掲載されているようなアルゴリズムをPythonで実装しているサイトを見つけました。
https://tjkendev.github.io/procon-library/python/index.html

以下の二つのアルゴリズムを組み合わせて、目的の関数を作ります。

多角形の点包含判定
https://tjkendev.github.io/procon-library/python/geometry/point_inside_polygon.html
凸多角形同士の交差判定/交点
https://tjkendev.github.io/procon-library/python/geometry/point_inside_polygon.html

　
関数の仕組み

1. 四角形の全頂点は選択範囲の内側か？
2. 四角形の辺と選択範囲の辺は重なるか？

この二つを調べていずれかでTrueならばよいことになります。（ですよね...?）

cross_rec.py

# 頂点は選択範囲の内側か？
# https://tjkendev.github.io/procon-library/python/geometry/point_inside_polygon.html より

def inside_polygon(p0, qs):
    cnt = 0
    L = len(qs)
    x, y = p0
    for i in range(L):
        x0, y0 = qs[i-1]; x1, y1 = qs[i]
        x0 -= x; y0 -= y
        x1 -= x; y1 -= y
        cv = x0*x1 + y0*y1
        sv = x0*y1 - x1*y0
        if sv == 0 and cv <= 0:
            return True
        if not y0 < y1:
            x0, x1 = x1, x0
            y0, y1 = y1, y0
        if y0 <= 0 < y1 and x0*(y1 - y0) > y0*(x1 - x0):
            cnt += 1
    return (cnt % 2 == 1)

# 四角形の辺と選択範囲の辺は重なるか？
# https://tjkendev.github.io/procon-library/python/geometry/point_inside_polygon.html より
def dot3(O, A, B):
    ox, oy = O; ax, ay = A; bx, by = B
    return (ax - ox) * (bx - ox) + (ay - oy) * (by - oy)
def cross3(O, A, B):
    ox, oy = O; ax, ay = A; bx, by = B
    return (ax - ox) * (by - oy) - (bx - ox) * (ay - oy)
def dist2(A, B):
    ax, ay = A; bx, by = B
    return (ax - bx) ** 2 + (ay - by) ** 2
def is_intersection(P0, P1, Q0, Q1):
    C0 = cross3(P0, P1, Q0)
    C1 = cross3(P0, P1, Q1)
    if C0 == C1 == 0:
        E0 = dot3(P0, P1, Q0)
        E1 = dot3(P0, P1, Q1)
        if not E0 < E1:
            E0, E1 = E1, E0
        return 0 <= E1 and E0 <= dist2(P0, P1)
    D0 = cross3(Q0, Q1, P0)
    D1 = cross3(Q0, Q1, P1)
    return C0 * C1 <= 0 and D0 * D1 <= 0

def convex_polygons_intersection(ps, qs):
    pl = len(ps); ql = len(qs)
    i = j = 0
    while (i < pl or j < ql) and (i < 2*pl) and (j < 2*ql):
        px0, py0 = ps0 = ps[(i-1)%pl]; px1, py1 = ps1 = ps[i%pl]
        qx0, qy0 = qs0 = qs[(j-1)%ql]; qx1, qy1 = qs1 = qs[j%ql]

        if is_intersection(ps0, ps1, qs0, qs1):
            return True

        ax = px1 - px0; ay = py1 - py0
        bx = qx1 - qx0; by = qy1 - qy0

        v = (ax*by - bx*ay)
        va = cross3(qs0, qs1, ps1)
        vb = cross3(ps0, ps1, qs1)

        if v == 0 and va < 0 and vb < 0:
            return 0
        if v == 0 and va == 0 and vb == 0:
            i += 1
        elif v >= 0:
            if vb > 0:
                i += 1
            else:
                j += 1
        else:
            if va > 0:
                j += 1
            else:
                i += 1
    return False


# ps は四角形
# qs は選択範囲
ps = [(2, 2), (5, 3), (4, 10), (2, 6)]
qs = [(3, 3), (4, 3), (3, 4), (3, 10)]


INSIDE_FLAG = False
#まずは頂点が選択範囲内かをチェック。p_in_vtは入っている頂点数のカウンター。
p_in_vt = 0
for vertices in ps:
    if inside_polygon(vertices,qs):
        p_in_vt += 1
if p_in_vt == 4:
    INSIDE_FLAG = True
#次に辺の重なりをチェック
if convex_polygons_intersection(ps, qs):
    INSIDE_FLAG = True

print(INSIDE_FLAG)

True

以上です。
もっと賢いやり方を知ってるよって方はコメント欄で教えてください。
(4/8 コードの間違いを修正。また、図表と文章内容を一部変更)