0. 前書き:大学図書館で面白い本を見つけた
とある日、大学の図書館をいつものように物色していると数学の棚にあった1冊の本を手に取った。
微分方程式で数学モデルを作ろう・日本評論社(書籍詳細はこちら)
微分方程式で様々な現象をモデル化しているようだ。Julia で数値計算だったり微分方程式を解く手段だったりを知った直後だったので練習したいと思い図書館から借りてきた。
この記事では、この書籍に書いてある「人口問題」について実際にJulia で解いてみたので報告する。
まあ、タイトルにもあるように「ロジスティック方程式」を解いてみたのだ。
#1. ロジスティック方程式とは
Wikipedia によると、
ロジスティック方程式(ロジスティックほうていしき、英語:logistic equation[1])は、生物の個体数の変化の様子を表す数理モデルの一種である。ある単一種の生物が一定環境内で増殖するようなときに、その生物の個体数(個体群サイズ)の変動を予測できる。人間の場合でいえば、人口の変動を表すモデルである。
と書かれている。人間で言うところの人口変動を表すモデル、これでなんとなく理解はしていただけただろう。
具体的に、ロジスティック方程式は
$$
\frac{dN}{dt} = \gamma N\left(1 - \frac{N}{N_{\infty}}\right)
$$
のように記述される。ここで、$N = N(t)$ は「任意の時刻$t$におけるとある国の総人口」を表す。$N_{\infty}$ は「人口が増加した上限」である。
これを微分積分学の知識を用いて厳密に解くと、
$$
N(t) = \frac{N_{\infty}}{1 - \left(1 - \frac{N_{\infty}}{N_0}\right)e^{-\gamma t}}
$$
となる。ここで初期条件を $N(0) = N_0$ としている。
定数について、今回は
N_0 = 3.9 \times 10^6 \\
N_{\infty} = 1.97 \times 10^8 \\
\gamma = 0.3134
とする。
#2. コードに落とし込む
それでは今回も Ordinary Differential Equations を参考にしながらコーディングしていこう。
using DifferentialEquations
using Plots; gr()
#微分方程式を定義
f(y , t) = 0.3134y*(1-y/1.97e8)
#初期値
y0 = 3.9e6
#時間間隔
tspan = (0.0, 70.0)
#微分方程式を解かせる
prob = ODEProblem(f, y0, tspan)
sol = solve(prob)
#グラフをplot
plot(sol; legend=:topleft , title = "PopulationProblem" , lw = 5 , label = "Numerical" , color =:black)
#厳密解を定義してグラフに追加する
g(t) = 1.97e8/(1 - (1 - 1.97e8/3.9e6)*exp.(-0.3134*t))
plot!(g , linestyle =:dash , lw = 3 , label = "Exact" , color =:red)
これを実行すると、きちんとグラフを出すことができた。$t \to \infty$ で$N(t) \to N_{\infty}$ に収束することは厳密解からも分かる。
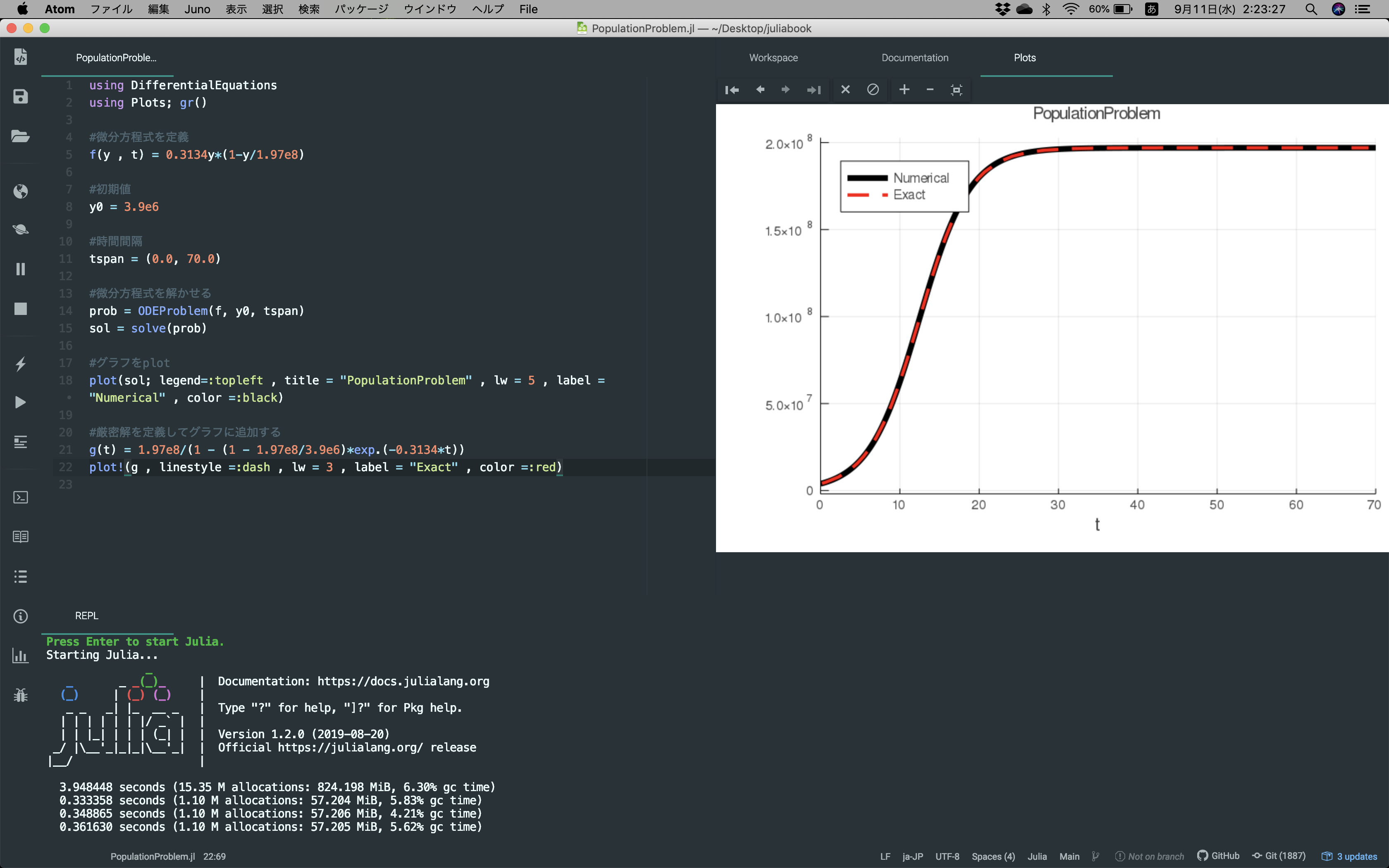
#3. 最後に
Twitterで助言をいただきながら今回も書くことができました。参考資料は本文中にリンクを埋めています。
Julia はとても簡単に記述できますね!