はじめに
スピーカーから発せられた音は片耳だけでなく両耳で聞こえてしまいます。これをクロストークと言うそうですが、それをなくすことはできるのでしょうか。疑問に思ったのでやってみます。
参考
以下を参考にしました。
猿渡洋, "4.逆フィルタによる音場再現技術", 映像情報メディア学会誌, 68(8), pp.612-615, 2014.
日本音響学会 音のなんでもコーナー > Q and A 055
手前味噌ですが、1年前に書いたブラインド音源分離も参考になりました。
トランスオーラルシステムは混合行列の要素が伝達関数になったようなものだと理解しました。
Qiita 独立成分分析を使ったブラインド音源分離
方針
実際にマイクロホンを使ってあれこれできたら楽しいですが、今回はプログラム上だけで試します。
簡単のため、スピーカーから両耳までの伝達関数は、反響音などを無視し距離によって生じる遅延のみを考慮します。
伝達関数を$G$、耳で聞く音を$e$、スピーカーが出す音を$s$とします。小文字は時間空間、大文字は周波数空間ということにします。
耳で聞く音は、スピーカーが出す音に各耳までのインパルス応答が畳み込まれた音になります。
\begin{align}
E_L &= S_L G_{11} + S_R G_{12}\\
E_R &= S_L G_{21} + S_R G_{22}\\
\end{align}
行列形式で書くと次のようになります。
\begin{align}
\left[ \matrix{E_L \\ E_R} \right] &= \left[ \matrix{G_{11} & G_{12} \\ G_{21} & G_{22}} \right] \left[ \matrix{S_L \\ S_R} \right]
\end{align}
今回はスピーカーでどんな音を出したら良いかを知りたいので、$S$について解きます。
\begin{align}
E &= GS \\
G^{-1}E &= G^{-1}GS \\
S &= G^{-1}E
\end{align}
聞きたい音をFFTして、それぞれの周波数ごとに上式の逆行列をかければどんな音を鳴らせばいいかわかりそうです。
試してみる
スピーカーと両耳の位置関係
適当な位置に両耳とスピーカーを配置します。
import numpy as np
import matplotlib.pyplot as plt
# eは耳、sはスピーカー
# 頭幅は160mmくらい
e_L_xy = np.array([-80.0,0])
e_R_xy = np.array([80.0,0])
s_L_xy = np.array([-160,200.0])
s_R_xy = np.array([200.0,230.0])
fig,axes = plt.subplots()
axes.set_aspect("equal")
axes.set_xlim(-200.0,300.0)
axes.set_ylim(-100.0,300.0)
axes.scatter(e_L_xy[0],e_L_xy[1])
axes.scatter(e_R_xy[0],e_R_xy[1])
axes.scatter(s_L_xy[0],s_L_xy[1])
axes.scatter(s_R_xy[0],s_R_xy[1])
インパルス応答
インパルス応答から$G$を求めます。スピーカーから発せられたパルス音は減衰もせず、反響もせず、ただ音速で伝播するのみとします。
v_s = 340.0e3 #音速 mm/s
fs = 192.0e3 #サンプリングレート Hz 適当
N = 8192 #FFTサンプル点数
t = np.arange(start=0.0,step=1/fs,stop=1/fs*N)
def calc_distance(p1,p2):
x, y = p1 - p2
return np.sqrt(x** 2 + y** 2)
def gen_pulse(t,delay):
"""
遅延時間に近い時刻にパルスを差し込む
"""
ix = np.argmin((delay-t)**2) #一番delayに近いインデックス
x = np.zeros(len(t))
x[ix] = 1.0
return x
g11 = gen_pulse(t, calc_distance(s_L_xy,e_L_xy) / v_s)
g12 = gen_pulse(t, calc_distance(s_R_xy,e_L_xy) / v_s)
g21 = gen_pulse(t, calc_distance(s_L_xy,e_R_xy) / v_s)
g22 = gen_pulse(t, calc_distance(s_R_xy,e_R_xy) / v_s)
g = np.array([[g11,g12],
[g21,g22]]).T #shape(8192, 2, 2)
fig,axes = plt.subplots()
axes.plot(t,g11)
axes.plot(t,g12)
axes.plot(t,g21)
axes.plot(t,g22)
axes.set_xlim(0.0,0.005)
インパルス応答はこんな感じになります。
スピーカーから適当な音を出したとき、耳で聞こえる音を計算する
ここでは、片方のスピーカーから出した音にインパルス応答を畳み込み、耳で聞こえる音をつくります。その耳で聞こえる音から、もとの信号が得られれば目的は達成です。
# 適当なサイン波 簡単のため片方のスピーカーからだけ音を出す
test_sig1 = np.sin(2.0*np.pi*100.0*t)
test_sig1[0:1000] = 0.0
test_sig1[3000:] = 0.0
test_sig2 = np.zeros(N)
この音$S$から耳で聞こえる音$E$を計算します。
\begin{align}
E &= GS
\end{align}
s = np.array([test_sig1,test_sig2]).T #shape(8192, 2)
S = np.fft.rfft(s,axis=0) #折返し周波数までFFT shape(4097, 2)
G = np.fft.rfft(g,axis=0) #伝達関数 shape(4097, 2, 2)
def dot_axis0(a,b):
x = []
for i in range(a.shape[0]):
x.append(a[i].dot(b[i]))
return np.array(x)
GS = dot_axis0(G,S) #shape(4097, 2)
gs = np.fft.irfft(GS,axis=0) #shape(8192, 2)
fig,axes = plt.subplots()
axes.plot(t,gs.T[0])
axes.plot(t,gs.T[1])
左耳と右耳で位相差のある信号が得られました。
耳で聞こえた音からスピーカーが出した音を逆算する
今度は耳で聞こえた音を出すにはどんな音をスピーカーから出せばいいか計算します。
$G$の逆行列を$E$にかけるだけです。
# Gの逆行列 直流成分は0なので逆行列はない。0で置き換え
G_inv = np.linalg.pinv(G) #shape(4097, 2, 2)
G_inv[0] = np.zeros(G_inv[0].shape)
G_inv_GS = dot_axis0(G_inv,GS) #shape(4097, 2)
g_inv_gs = np.fft.irfft(G_inv_GS,axis=0) #shape(8192, 2)
fig,axes = plt.subplots()
axes.plot(t,g_inv_gs.T[0])
axes.plot(t,g_inv_gs.T[1])
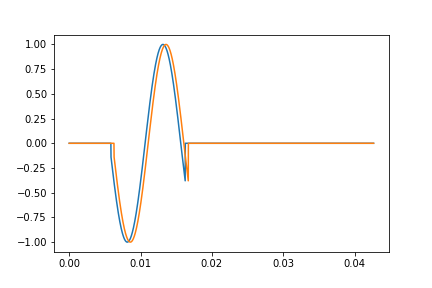
だいたい元通りです。計算方法はこれで良さそうだとわかりました。
片耳だけ聞こえる音を2つのスピーカーでつくれるか
本題をやってみます。片方だけの音は上で使ったものを流用します。
E = G_inv_GS #上の図、片側だけ音がある
S = dot_axis0(G_inv,E)
s = np.fft.irfft(S,axis=0)
fig,axes = plt.subplots()
axes.plot(t,s.T[0])
axes.plot(t,s.T[1])
念の為、もとに戻るかやってみます。
GS = dot_axis0(G,S)
gs = np.fft.irfft(GS,axis=0)
もとの信号に絶壁な部分があるので高周波成分が多くなってしまいましたが、平滑化した信号なら次のようになります。
まとめ
トランスオーラルシステムの基礎を単純化したモデルを用いて学習しました。現実のオーディオシステムに使うためには、頭部位置や音速の変化によって伝達関数が変動するため、今回の方法だけだとうまくいかなさそうです。狙った音が聞こえる範囲も考える必要がありますね。マイクが用意できたら本当に片耳だけに音を伝えられるか試してみたいと思います。