CTスキャンの断面再構成アルゴリズム ML-EM法の実装

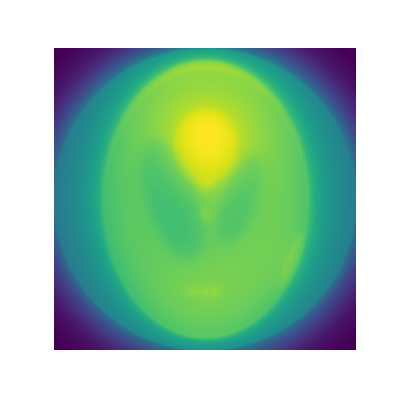
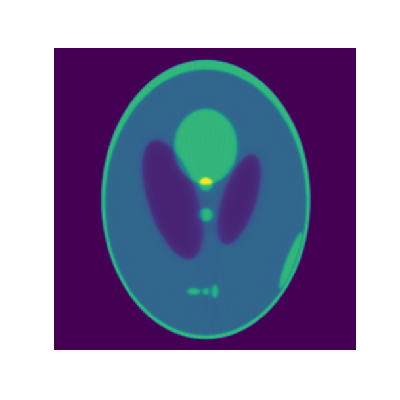
はじめに

健康診断などでCTスキャンを受ける機会がありました。
どうやって断層の画像を再構成しているのか気になったので、調べて実装してみようと思います。

X線CTの画像再構成アルゴリズムは、従来はフィルタ補正逆投影法(FBP)が用いられていましたが、X線量を減らした場合には得られる画質に限界があるそうです。
そこで、計算時間はFBPより増えるものの、明瞭な画像が得られる統計的手法の一つ、ML-EM法をここでは試していきたいと思います。

ML-EM法は、実測の投影データをもとに再構成した画像から、再び投影データを作り、それができるだけ実測値に近づくように逐次更新していくアルゴリズムです。

参考

以下を参考にしました。

篠原 広行, 断層映像法の基礎 第32回 ML-EM法とOS-EM法

田中敏幸, 解説:特集 電磁界モデリングを用いる計測技術の基礎と新展開 X線CTの原理・現状とさらなる画像の高品質化

アルゴリズム

まず始めに、アルゴリズムの流れを書きます。その後に、言葉の意味の説明などをします。

1. k番目の画像からk番目の投影を作成する。最初の画像は、値が全て1の画像を使う
2. k番目の投影と実測した投影データの比を求める　実測した投影データ/(1)の投影データ
3. その比を逆投影する
4. k番目の画像に逆投影した画像をかけて、k+1番目の画像に更新する

投影、逆投影について説明し、その後にML-EM法の実装を行います。

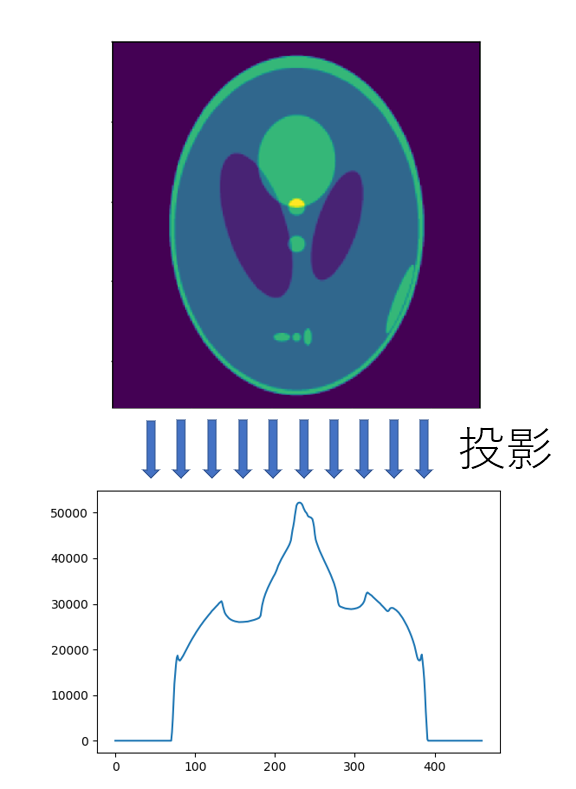
計測データ 投影

計測データは、一方向からX線を照射して、光の一部が人体に吸収された影です。

CTスキャンでは、この投影をいろいろな角度から行います。
ここでは、360度を200分割(1.8度刻み)で撮影したデータを作成しました。

計測データを用意したプログラムは以下の通りです。

import numpy as np
import matplotlib.pyplot as plt
from pathlib import Path
import cv2

def rotate_center(image, angle):
    """
    画像の真ん中を中心にして，回転させる
    image : 画像
    angle : 回転させる角度[deg]
    """
    h, w = image.shape[:2]
    affine = cv2.getRotationMatrix2D((w/2.0, h/2.0), angle, 1.0) #画像の中心の座標,回転させたい角度,拡大比率
    return cv2.warpAffine(image, affine, (w, h))

def circle_mask(img):
    """
    内接円の領域を残して，他を0でマスクする
    """
    x = np.linspace(-1.0,1.0,img.shape[0])
    X,Y = np.meshgrid(x,x)
    distance_map = np.sqrt(X**2+Y**2) #中心からの距離
    img[distance_map>=1.0] = 0.0
    return img

def forward_projection(img,theta):
    rot_img = rotate_center(img, theta)
    return np.sum(rot_img,axis=0)

theta_array = np.linspace(0.0,360.0,200,endpoint=False)

true_img = cv2.imread("CT_img.png",cv2.IMREAD_GRAYSCALE) #CT画像 これをもとに戻すのが目標
true_img = circle_mask(true_img) #円形マスク

forward_projection_array_meas = []
for theta in theta_array:
    forward_projection_array_meas.append(forward_projection(true_img,theta))
forward_projection_array_meas = np.asarray(forward_projection_array_meas)

fig,axes = plt.subplots()
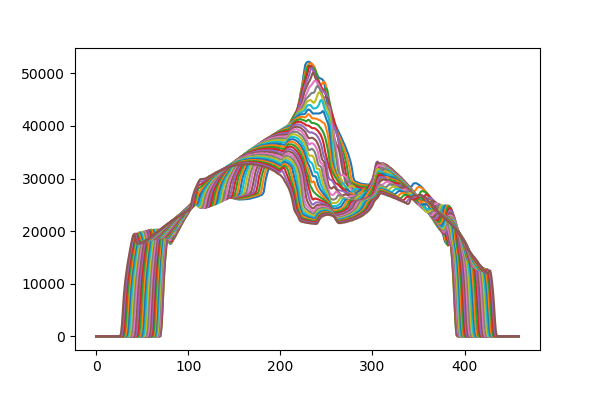
for i in range(200):
    axes.plot(forward_projection_array_meas[i])

#参考にしたPDFでは画像にしてありました
fig,axes = plt.subplots()
axes.imshow(forward_projection_array_meas,aspect=3)

参考にした論文では、投影データを並べて画像化してありましたので、ここでもそれと比較するために掲載しておきます。

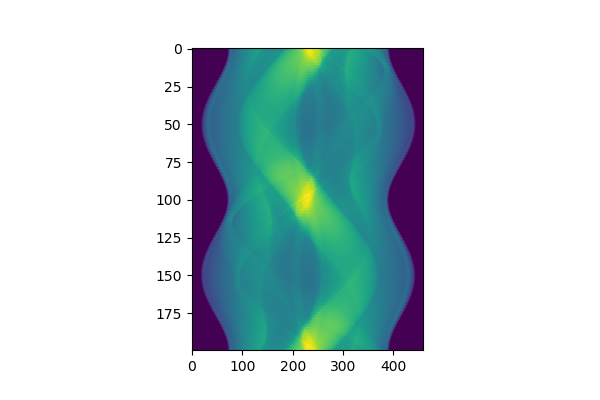
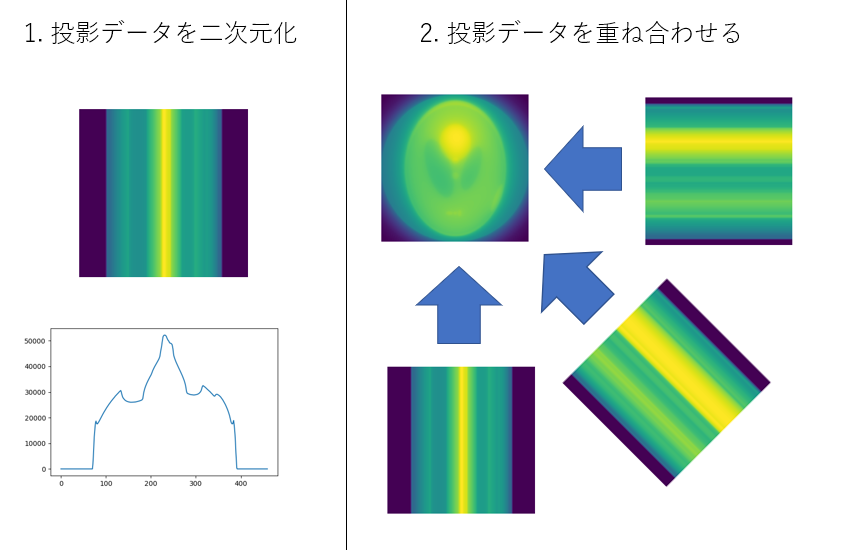
逆投影

逆投影は、投影データをもとの画像と同じ次元になるようタイル状に敷き詰め、足し合わせる操作です。

ML-EM法の実装

ML-EM法のアルゴリズムの則って実装します。

def rotate_center(img, angle):
    """
    画像の真ん中を中心にして，回転させる
    image : 画像
    angle : 回転させる角度[deg]
    """
    h, w = img.shape[:2]
    affine = cv2.getRotationMatrix2D((w/2.0, h/2.0), angle, 1.0) #画像の中心の座標,回転させたい角度,拡大比率
    rot_img = cv2.warpAffine(img, affine, (w, h))
    return rot_img

def circle_mask(img):
    """
    内接円の領域を残して，他を0でマスクする
    """
    x = np.linspace(-1.0,1.0,img.shape[0])
    X,Y = np.meshgrid(x,x)
    distance_map = np.sqrt(X**2+Y**2) #中心からの距離
    img[distance_map>=1.0] = 0.0
    return img

def forward_projection(img, theta_array):
    """
    k番目の画像に回転を加えて投影する操作を繰り返す
    """
    img = circle_mask(img)
    forward_projection_array = []
    for theta in theta_array:
        rot_img_sum = np.sum(rotate_center(img, theta),axis=0)
        forward_projection_array.append(rot_img_sum)
    forward_projection_array = np.asarray(forward_projection_array)
    return forward_projection_array

def back_projection(img_shape, theta_array, forward_projection_array):
    """
    逆投影する
    img_shape : 画像サイズ
    theta_array : 角度データ
    forward_projection_array : 計測データ
    """
    back_pro_img = np.zeros(img_shape,dtype=np.float64)

    for i,theta in enumerate(theta_array):
        tile_img = np.tile(forward_projection_array[i],[img_shape[0],1]) #axis=0方向に敷き詰める
        tile_img = rotate_center(tile_img, -theta) #回転
        back_pro_img += tile_img
    back_pro_img /= theta_array.shape[0] #重ね合わせた回数で割る
    return back_pro_img

本来であれば、k-1番目とk番目の画像の差がいくら以下になったら反復をやめるなどとしますが、ここでは簡単のために適当に60回くらいにしました。

k_img = np.ones_like(true_img) # 最初の画像

for i in range(60):
    forward_projection_array_k = forward_projection(k_img, theta_array)+1.0e-12 # 1.k番目の画像からk番目の投影を作成する 0divを避けるため，1.0e-12を足した
    forward_pro_ratio = forward_projection_array_meas / forward_projection_array_k # 2.k番目の投影と実測した投影データの比を求める　実測した投影データ/(1)の投影データ
    back_pro_img = back_projection(true_img.shape, theta_array, forward_pro_ratio) #3. その比を逆投影する
    k_img *= back_pro_img #4. k番目の画像に逆投影した画像をかけて，k+1番目の画像に更新する

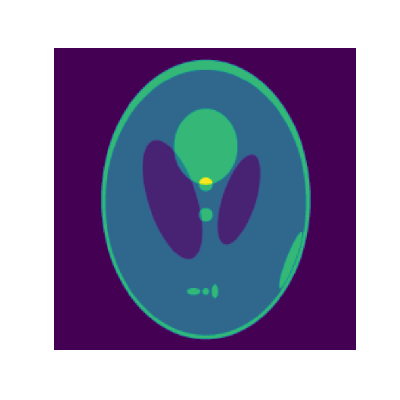
結果

もとの画像

反復1回目

反復60回目

もとの画像より若干ぼやけるものの、よく再現されています。

まとめ

CT画像の再構成手法の一つであるML-EM法を実装し、サンプル画像から計測データを作成し、再構成を行いました。

本来であれば、回転したあとの座標が非整数値であるとき、輝度を複数のピクセルに分割する操作が必要です。参考文献では、EM-ML法の定式化で変数Cにあたります。openCVの画像の回転はバイリニア法で補間されるので、変換前と後で画像の輝度の総和が保たれません。
ただ、趣味でやってみる分には大した問題ではないかなと思います。

実際のデータで試してみたいですが、X線CT装置はとても買えません。
寒天に少し小麦粉でも混ぜて、バックライトで照らしながら撮影したら、X線CT画像のような投影データが得られるかなと思います。
機会があったらやります。