はじめに
RとStanではじめる ベイズ統計モデリングによるデータ分析入門を読みました。わかりやすく、詰まることなく読みすすめることができました。おすすめです。
さらに理解を深めるために、本の内容をなぞって試したいと思います。こちらの書籍ではRとstanを使用していますが、ここではPythonとPystanを使います。
この投稿の大まかな内容は次の通りです。
- ベイズの定理
- MCMC法
- Pystanの使い方
- 単回帰モデル
単回帰モデルという単純なモデルを通して、ベイズ推定の流れとPystanの使い方を学びます。
0. モジュール
ここで予め必要になるモジュールをインポートしておきます。
import numpy as np
import matplotlib.pyplot as plt
import pystan
import arviz
plt.rcParams["font.family"] = "Times New Roman" #全体のフォントを設定
plt.rcParams["xtick.direction"] = "in" #x軸の目盛線を内向きへ
plt.rcParams["ytick.direction"] = "in" #y軸の目盛線を内向きへ
plt.rcParams["xtick.minor.visible"] = True #x軸補助目盛りの追加
plt.rcParams["ytick.minor.visible"] = True #y軸補助目盛りの追加
plt.rcParams["xtick.major.width"] = 1.5 #x軸主目盛り線の線幅
plt.rcParams["ytick.major.width"] = 1.5 #y軸主目盛り線の線幅
plt.rcParams["xtick.minor.width"] = 1.0 #x軸補助目盛り線の線幅
plt.rcParams["ytick.minor.width"] = 1.0 #y軸補助目盛り線の線幅
plt.rcParams["xtick.major.size"] = 10 #x軸主目盛り線の長さ
plt.rcParams["ytick.major.size"] = 10 #y軸主目盛り線の長さ
plt.rcParams["xtick.minor.size"] = 5 #x軸補助目盛り線の長さ
plt.rcParams["ytick.minor.size"] = 5 #y軸補助目盛り線の長さ
plt.rcParams["font.size"] = 14 #フォントの大きさ
plt.rcParams["axes.linewidth"] = 1.5 #囲みの太さ
1. ベイズの定理
ベイズ推定は、ベイズの定理が基礎になっています。
p(\theta|x)=p(\theta) \frac{p(x|\theta)}{\int p(x|\theta)p(\theta)d\theta}
ここで$\theta$はパラメータ、$p(\theta)$は事前分布、$p(x|\theta)$は$\theta$であるときの$x$の条件付き確率(尤度)、$p(\theta|x)$は事後分布です。
日本語で書くと、このようになります。
(事後分布) = (事前分布) \times \frac{(尤度)}{(周辺尤度)}
また、周辺尤度は事後分布の積分値を1にする正規化定数です。従って、周辺尤度の項を省略して以下の関係が成り立ちます。
(事後分布) \propto (事前分布) \times (尤度)
1.1 例
ある正規分布に従う確率変数$x$を例に、平均値をベイズ推定することを考えます。標準偏差は1であるとわかっているとします。その正規分布の確率密度関数は以下のようになります。
\begin{align} p(x|\mu, \sigma=1) &= \frac{1}{\sqrt{2\pi\sigma^2}}\exp{\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)} \\
&= \frac{1}{\sqrt{2\pi}}\exp{\left(-\frac{(x-\mu)^2}{2}\right)} \end{align}
np.random.seed(seed=1) #乱数の種
mu = 5.0 #平均
s = 1.0 #標準偏差
N = 10 #個数
x = np.random.normal(mu,s,N)
print(x)
array([6.62434536, 4.38824359, 4.47182825, 3.92703138, 5.86540763,
2.6984613 , 6.74481176, 4.2387931 , 5.3190391 , 4.75062962])
上記のデータが得られる確率(尤度)を求めます。データは$D$とします。それぞれのデータを得る事象は独立であるため、1つ1つのデータが得られる確率をかけ合わせます。
f(D|\mu) = \prod_{i=0}^{N-1} \frac{1}{\sqrt{2\pi}}\exp{\left(-\frac{(x_i-\mu)^2}{2}\right)}
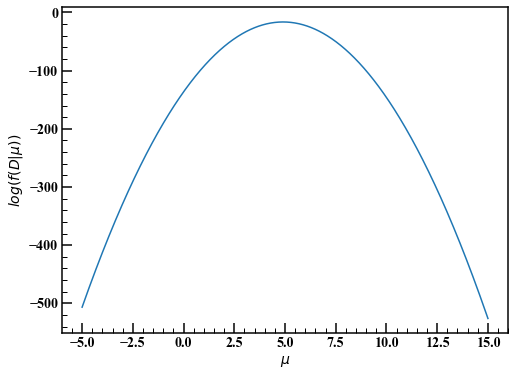
書籍にはありませんが、上の関数を可視化してみます。ここで尤度関数の最大値を取って平均は5だと決める(点推定)のを最尤法と言うそうですね。
mu_ = np.linspace(-5.0,15.0,1000)
f_D = 1.0
for x_ in x:
f_D *= 1.0/np.sqrt(2.0*np.pi) * np.exp(-(x_-mu_)**2 / 2.0) #尤度関数
fig,axes = plt.subplots(figsize=(8,6))
axes.plot(mu_,np.log(f_D))
axes.set_xlabel(r"$\mu$")
axes.set_ylabel(r"$log (f(D|\mu))$")
ベイズ推定の話に戻って、事前分布を決めます。パラメータである$\mu$について前もって知識がないときは、根拠不十分の原則に従って、とりあえず広い分布を考えます。今回は分散10000で平均0の正規分布にします。
$$f(\mu) = \frac{1}{\sqrt{20000\pi}}\exp{\left(-\frac{(x-\mu)^2}{20000}\right)}$$
パラメータ$\mu$の事後分布の確率密度関数$f(\mu|D)$は、$(事前分布) \times (尤度)$に比例するのでした。
$$\begin{eqnarray}f(\mu|D) &\propto& f(\mu) f(D|\mu) \
&=& \left[ \frac{1}{\sqrt{20000\pi}}\exp{\left(-\frac{\mu^2}{20000}\right)} \right]
\left[ \prod_{i=0}^{N-1} \frac{1}{\sqrt{2\pi}}\exp{\left(-\frac{(x_i-\mu)^2}{2}\right)} \right]
\end{eqnarray}$$
ベイズ推定では、事後分布が複雑で積分が難しいことがあります。せっかく事後分布の確率密度関数を得ても、積分できなければ、例えば平均値が4から6の間にある確率などが求められません。そのような場合に活躍するのがMCMC法というわけです。今回の例ではパラメータが1つなので、MCMC法ではなく$\mu$について分割して事後分布の様子を見てみます。
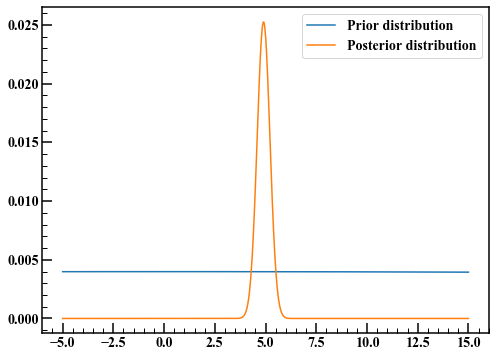
f_mu = 1.0/np.sqrt(20000.0*np.pi) * np.exp(-mu_**2.0 / 20000) #事前分布
f_mu_poster = f_mu * f_D #(事前分布)×(尤度)
f_mu_poster /= np.sum(f_mu_poster) #積分値を1にする
fig,axes = plt.subplots(figsize=(8,6))
axes.plot(mu_,f_mu,label="Prior distribution")
axes.plot(mu_,f_mu_poster,label="Posterior distribution")
axes.legend(loc="best")
事前分布は裾の広い分布でしたが、ベイズ更新された事後分布では裾が狭くなっています。最尤法で得られたように、事後分布の期待値は5にあるように見えます。
2. MCMC法
MCMC法とは、マルコフ連鎖モンテカルロ法の略です。ある時点の値が1つ前の時点の影響だけを受けるマルコフ連鎖を利用した乱数生成手法です。ベイズ推定では、パラメータの事後分布に従う乱数をMCMC法で生成し、積分の代わりに利用します。例えば事後分布の期待値を求めようと思えば、乱数たちの平均を計算すれば求まります。
2.1 メトロポリス・ヘイスティングス法(MH法)
ある確率分布に従う乱数を発生させるアルゴリズムについて説明します。簡単のため、推定するパラメータは1つだけとします。
- 乱数の初期値$\hat{\theta}$を適当に決める。
- 平均0、分散$\sigma^2$の正規分布に従う乱数を生成する。
- それの乱数と初期値$\hat{\theta}$の和を計算する。これを$\theta^{suggest}$とする。
- $\hat{\theta}$と$\theta^{suggest}$の確率密度の比を計算する。
- 確率密度の比が1より大きければ$\theta^{suggest}$を採用、1以下ならその値を確率として、採用または不採用にする。
採用された乱数を初期値として、何度も繰り返します。確率密度が高いところほど乱数が採用されやすくなるので、確率分布に従いそうな感じがします。
1.1の例を再び用いて、事後分布に従う乱数を上記の方法で生成してみます。
np.random.seed(seed=1) #乱数の種
def posterior_dist(mu): #事後分布
#(事前分布)×(尤度)
return 1.0/np.sqrt(20000.0*np.pi) * np.exp(-mu**2.0 / 20000) \
* np.prod(1.0/np.sqrt(2.0*np.pi) * np.exp(-(x-mu)**2 / 2.0))
def MH_method(N,s):
rand_list = [] #採用した乱数
theta = 1.0 #1. 初期値を適当に決める
for i in range(N):
rand = np.random.normal(0.0,s) #2. 平均0、標準偏差sの正規分布に従う乱数を生成する
suggest = theta + rand #3.
dens_rate = posterior_dist(suggest) / posterior_dist(theta) #4. 確率密度の比
# 5.
if dens_rate >= 1.0 or np.random.rand() < dens_rate:
theta = suggest
rand_list.append(theta)
return rand_list
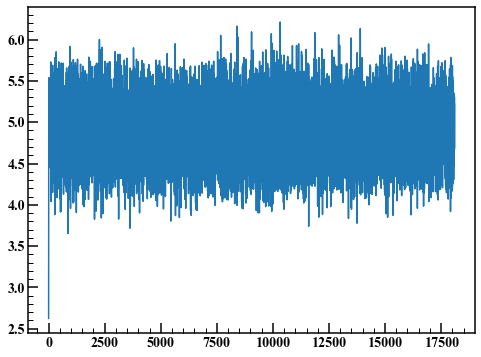
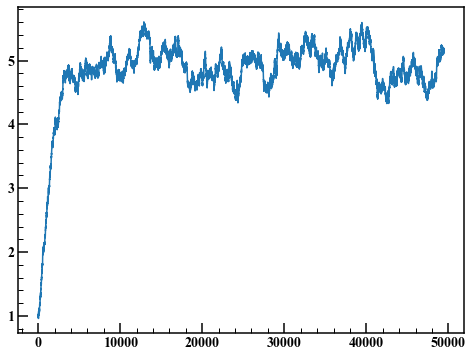
手順2で発生させる乱数の標準偏差を1として、1から5の手順を50000回繰り返します。
rand_list = MH_method(50000,1.0)
len(rand_list) / 50000
0.3619
乱数が採用される確率を受容率と言います。今回は36.2%でした。
fig,axes = plt.subplots(figsize=(8,6))
axes.plot(rand_list)
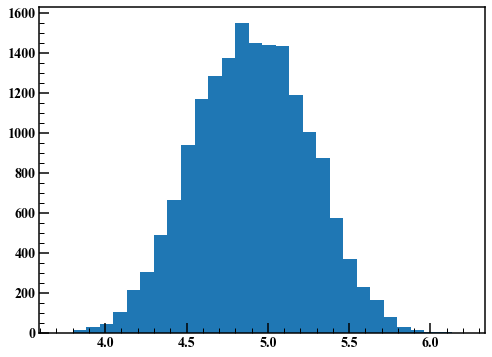
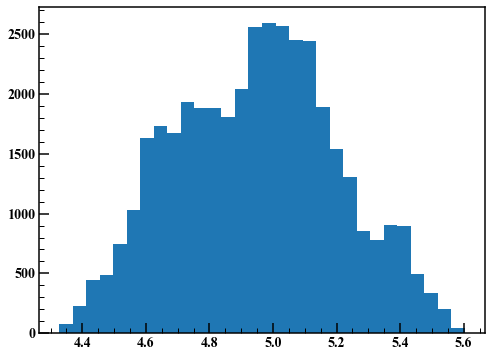
このようなグラフをトレースプロットと呼びます。始めの何点かは初期値の影響を受けて非定常になっています。ここでは始めの1000点を捨ててヒストグラムを描きます。
fig,axes = plt.subplots(figsize=(8,6))
axes.hist(rand_list[1000:],30)
いい感じの結果が得られました。
次に手順2で発生させる乱数の標準偏差を0.01にして同じことを繰り返します。
rand_list = MH_method(50000,0.01)
len(rand_list) / 50000
0.98898
受容率が98.9%と大きくなりました。
fig,axes = plt.subplots(figsize=(8,6))
axes.plot(rand_list)
始めの10000点を捨ててヒストグラムを描画します。
fig,axes = plt.subplots(figsize=(8,6))
axes.hist(rand_list[10000:],30)
ご覧のように、MH法は手順2で使用する乱数の分散によって結果が変わってしまいます。この問題を解決するためのアルゴリズムとしてハミルトニアン・モンテカルロ法などがあります。Stanは色々と賢いアルゴリズムが実装されているので、その恩恵に与ります。
3. Pystanの使い方
Stanコードは、dataブロック、parametersブロック、modelブロックが必要です。dataブロックは使用するデータの情報、parametersブロックは推定したいパラメータたち、modelブロックは事前分布や尤度を記述します。generated quantitiesブロックは推定したパラメータを使って乱数を生成したりできます。記述方法はStanコード中のコメントに書きました。
stan_code = """
data {
int N; // サンプルサイズ
vector[N] x; // データ
}
parameters {
real mu; // 平均
real<lower=0> sigma; // 標準偏差 <lower=0>は、0以上の値しか取らないという指定
}
model {
// 平均mu、標準偏差sigmaの正規分布
x ~ normal(mu, sigma); // "~"記号は、左辺が右辺の分布に従うことを表す
}
generated quantities{
// 事後予測分布を得る
vector[N] pred;
// Pythonと違って、添字は1から始まる
for (i in 1:N) {
pred[i] = normal_rng(mu, sigma);
}
}
"""
Stanコードをコンパイルします。
sm = pystan.StanModel(model_code=stan_code) #stanコードのコンパイル
使用するデータをまとめます。上記Stanコードのdataブロックで宣言した変数名と対応させます。
# データをまとめる
stan_data = {"N":len(x), "x":x}
MCMCを実行する前に、samplingメソッドの引数について説明します。
- 繰り返し数 iter : 生成される乱数の数。何も指定しないとデフォルト2000になります。収束が悪いときは大きな値にすることがあります。
- バーンイン期間 warmup : 2.1のトレースプロットのように、始めは初期値の影響を受けます。その影響を避けるため、warmupで指定した点数分を捨てます。
- 間引き thin : thin個に1個の乱数を採用します。MCMC法はマルコフ連鎖を利用しているため、1時点前の影響を受け、自己相関性を持ちます。この影響を低減します。
- チェーン chains : 収束の評価のため、初期値を変えてchains回MCMCによる乱数生成を行います。それぞれの試行の結果が同じようであれば、収束したと判断することができます。
MCMCの実行をします。
# MCMCの実行
mcmc_normal = sm.sampling(
data = stan_data,
iter = 2000,
warmup = 1000,
chains = 4,
thin = 1,
seed = 1
)
その結果を表示します。使用したデータは、平均5、標準偏差1の正規分布に従う乱数でした。muが平均、sigmaが標準偏差を表します。
結果の表の各項目について説明します。
- mean : 事後分布の期待値
- se_mean : 事後分布の期待値を有効なサンプル数の平方根で割った値1
- sd : 事後分布の標準偏差
- 2.5% - 97.5% : ベイズ信用区間。事後分布に従う乱数を小さい順に並べて、2.5%地点から97.5%地点に該当する値を調べます。この差を取れば、95%ベイズ信用区間(信頼区間)を得ることができます。
- n_eff : 採用された乱数の個数
- Rhat : 同一チェーン内での乱数の分散の平均値と異なるチェーンを含めたすべての乱数の分散の比を表します。chainsが3以上のとき、Rhatが1.1より小さくなるのが目安らしいです。
- lp__ : 対数事後確率2
mcmc_normal
Inference for Stan model: anon_model_710b192b75c183bf7f98ae89c1ad472d.
4 chains, each with iter=2000; warmup=1000; thin=1;
post-warmup draws per chain=1000, total post-warmup draws=4000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
mu 4.9 0.01 0.47 4.0 4.61 4.89 5.18 5.87 1542 1.0
sigma 1.46 0.01 0.43 0.89 1.17 1.38 1.66 2.58 1564 1.0
pred[1] 4.85 0.03 1.58 1.77 3.88 4.86 5.83 8.0 3618 1.0
pred[2] 4.9 0.03 1.62 1.66 3.93 4.9 5.89 8.11 3673 1.0
pred[3] 4.87 0.03 1.6 1.69 3.86 4.85 5.86 8.14 3388 1.0
pred[4] 4.86 0.03 1.57 1.69 3.89 4.87 5.81 7.97 3790 1.0
pred[5] 4.88 0.03 1.6 1.67 3.89 4.89 5.89 7.98 3569 1.0
pred[6] 4.86 0.03 1.61 1.56 3.94 4.87 5.81 8.01 3805 1.0
pred[7] 4.89 0.03 1.6 1.7 3.9 4.88 5.86 8.09 3802 1.0
pred[8] 4.88 0.03 1.61 1.62 3.87 4.88 5.9 8.12 3210 1.0
pred[9] 4.87 0.03 1.6 1.69 3.86 4.87 5.85 8.1 3845 1.0
pred[10] 4.91 0.03 1.63 1.73 3.91 4.88 5.9 8.3 3438 1.0
lp__ -7.63 0.03 1.08 -10.48 -8.03 -7.29 -6.85 -6.57 1159 1.0
Samples were drawn using NUTS at Wed Jan 1 14:32:42 2020.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
fit.plot()としたところ、WARNINGがでたのでそれに従います。
WARNING:pystan:Deprecation warning.
PyStan plotting deprecated, use ArviZ library (Python 3.5+).
pip install arviz; arviz.plot_trace(fit))
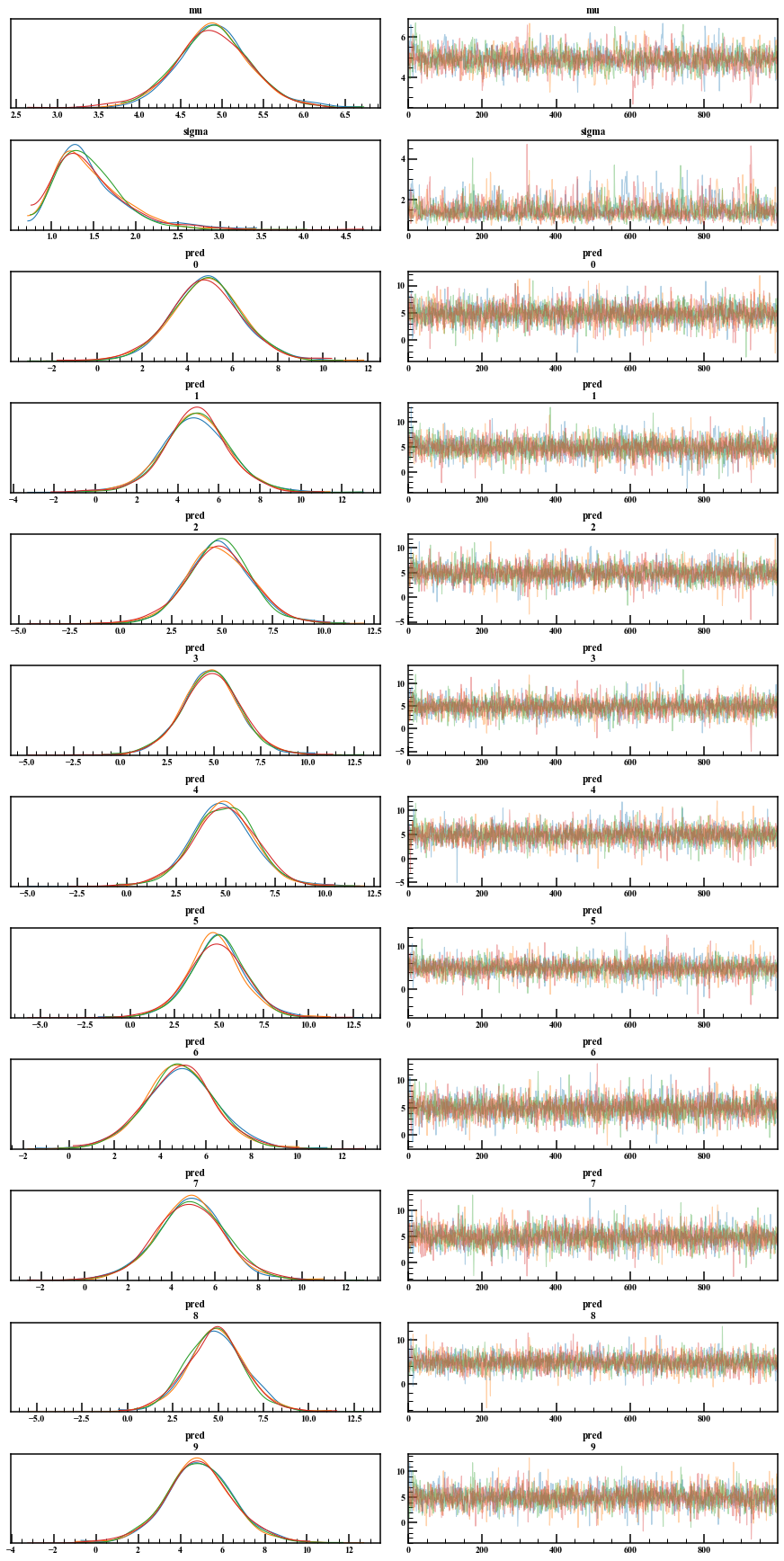
簡単にトレースプロットや事後分布の確認ができます。
arviz.plot_trace(mcmc_normal)
MCMCサンプルを直接いじって何かしたいときや、グラフをもっとこだわりたいときはextractで取り出せます。デフォルトではpermuted=Trueで、順番が混ぜられた乱数が返ってきます。トレースプロットは時系列であってほしいので、この引数はFalseにしておきます。また、inc_warmupはバーンイン期間を含めるか否かです。それとfit["変数名"]でもバーンイン期間を除いた乱数は得られました。
mcmc_extract = mcmc_normal.extract(permuted=False, inc_warmup=True)
mcmc_extract.shape
(2000, 4, 13)
次元を確認すると、(iter,chains,パラメータの数)になっています。先程のグラフの数は12なのに13次元目がありますが、プロットして確認したところlp__のようです。
4. 単回帰分析
ここまでのまとめとして、単回帰分析をベイズ推定で行います。$y$を応答変数、$x$を説明変数とします。$y$は、傾き$a$と切片$b$を用いて平均$\mu=ax + b$、標準偏差$\sigma^2$の正規分布に従うとします。
\begin{align}
\mu &= ax + b \\
y &\sim \mathcal{N}(\mu,\sigma^2)
\end{align}
他の単回帰分析の説明でよく見られる表記も示します。
\begin{align}
y &= ax + b + \varepsilon \\
\varepsilon &\sim \mathcal{N}(0,\sigma^2)
\end{align}
上2式はどちらも同じです。最初に示した式のほうがStanコードを書くのに便利です。
今回の例では$y$が得られる過程を決めて、そこから値をサンプリングしてベイズ推定するという流れですが、実際のデータでは、データが得られる過程を考えて、ベイズ推定をして結果を見て、モデルを修正する試行錯誤をします。
4.1 データの確認
まずは、使用するデータを作成します。
np.random.seed(seed=1) #乱数の種
a,b = 3.0,1.0 #傾きと切片
sig = 2.0 #標準偏差
x = 10.0* np.random.rand(100)
y = a*x + b + np.random.normal(0.0,sig,100)
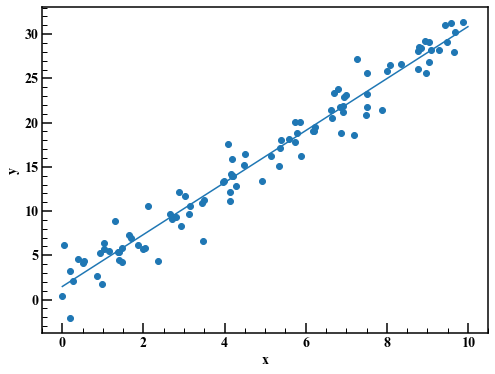
プロットして確認します。合わせて最小二乗法による線形回帰も表示します。
a_lsm,b_lsm = np.polyfit(x,y,1) #最小二乗法で線形回帰 (2.936985017531063, 1.473914508297817)
fig,axes = plt.subplots(figsize=(8,6))
axes.scatter(x,y)
axes.plot(np.linspace(0.0,10.0,100),a_lsm*np.linspace(0.0,10.0,100)+b_lsm)
axes.set_xlabel("x")
axes.set_ylabel("y")
4.2 データ生成過程の考察とStanコードの作成
データを作成した過程をすっかり忘れたとして、グラフを見て$y$と$x$は比例関係にありそうだと考えます。ばらつきは正規分布に従っていると仮定して、Stanコードを書きます。
stan_code = """
data {
int N; // サンプルサイズ
vector[N] x; // データ
vector[N] y; // データ
int N_pred; // 予測対象のサンプルサイズ
vector[N_pred] x_pred; // 予測対象のデータ
}
parameters {
real a; // 傾き
real b; // 切片
real<lower=0> sigma; // 標準偏差 <lower=0>は、0以上の値しか取らないという指定
}
transformed parameters {
vector[N] mu = a*x + b;
}
model {
// b ~ normal(0, 1000) 事前分布の指定
// 平均mu、標準偏差sigmaの正規分布
y ~ normal(mu, sigma); // "~"記号は、左辺が右辺の分布に従うことを表す
}
generated quantities {
vector[N_pred] y_pred;
for (i in 1:N_pred) {
y_pred[i] = normal_rng(a*x_pred[i]+b, sigma);
}
}
"""
新たに登場したtransformed parametersブロックはparametersブロックで宣言した変数を使って新しい変数を作成できます。今回は単純な式なのであまり差がありませんが、複雑な式であればこうすると見通しが良くなります。また、事前分布を指定するときはコメントアウトしてあるmodelブロックの"b ~ normal(0, 1000)"のように書きます。
4.3 MCMCの実行
Stanコードをコンパイルし、MCMCを実行します。
sm = pystan.StanModel(model_code=stan_code) #stanコードのコンパイル
x_pred = np.linspace(0.0,11.0,200)
stan_data = {"N":len(x), "x":x, "y":y, "N_pred":200, "x_pred":x_pred}
# MCMCの実行
mcmc_linear = sm.sampling(
data = stan_data,
iter = 4000,
warmup = 1000,
chains = 4,
thin = 1,
seed = 1
)
4.4 結果の確認
print(mcmc_linear)
Inference for Stan model: anon_model_28ac7b1919f5bf2d52d395ee71856f88.
4 chains, each with iter=4000; warmup=1000; thin=1;
post-warmup draws per chain=3000, total post-warmup draws=12000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
a 2.94 9.0e-4 0.06 2.82 2.89 2.94 2.98 3.06 4705 1.0
b 1.47 5.1e-3 0.35 0.79 1.24 1.47 1.71 2.16 4799 1.0
sigma 1.83 1.7e-3 0.13 1.59 1.74 1.82 1.92 2.12 6199 1.0
mu[1] 13.72 1.8e-3 0.19 13.35 13.59 13.72 13.85 14.09 10634 1.0
mu[2] 22.63 2.2e-3 0.24 22.16 22.47 22.63 22.78 23.1 11443 1.0
Samples were drawn using NUTS at Wed Jan 1 15:07:22 2020.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
とても長い出力なので省略してあります。Rhatを見ると収束は問題なさそうです。事後予測分布から95%信用区間を図示します。
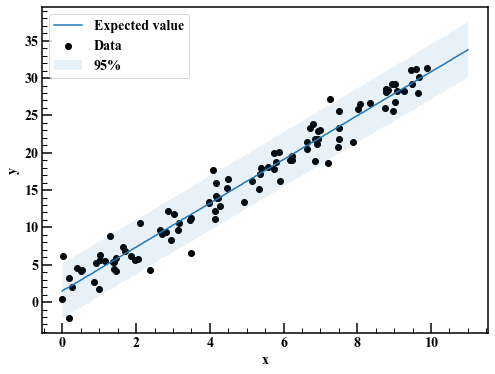
reg_95 = np.quantile(mcmc_linear["y_pred"],axis=0,q=[0.025,0.975]) #事後予測分布
fig,axes = plt.subplots(figsize=(8,6))
axes.scatter(x,y,label="Data",c="k")
axes.plot(x_pred,np.average(mcmc_linear["y_pred"],axis=0),label="Expected value")
axes.fill_between(x_pred,reg_95[0],reg_95[1],alpha=0.1,label="95%")
axes.legend(loc="best")
axes.set_xlabel("x")
axes.set_ylabel("y")
概ね良さそうです。
まとめ
単回帰モデルのベイズ推定を通して、ベイズ推定の流れとStanの使い方を学びました。もう一度ベイズ推定の流れを記録しておきます。
- データの確認 : グラフにプロットするなどして、データの構造を掴みます。
- データ生成過程の考察とStanコードの作成 : データの構造を数式化してStanコードを書きます。
- MCMCの実行 : MCMCを実行して、事後分布を得ます。
- 結果の確認 : 結果を確認して、繰り返しモデルの修正を行います。
今回は単純なモデルを使用しましたが、次回は状態空間モデルなどのより汎用的なモデルで試したいと思います。