はじめに
まず私はプログラマではありません.その上,今回が初めてのQiitaへの投稿です.
何か間違っていることが多分にあると思いますので,誤りを見つけたら教えて頂けるとありがたいです.いかようにでも修正します.
目的
オシロスコープなどで計測した離散信号の微分を差分法で行うためには,サンプリングレートを高く設定し,差分の時間刻み幅を小さくする必要があります.
最近,長時間の測定が必要でオシロスコープのサンプリングレートが高くとれない状況に陥りました.
そこでFFTを使用した補間方法を応用して,微分を行う方法を適用することを考えました.
参考
FFTで補間する方法を思いつきgoogleで検索してみたところ,当然ですが先駆者は沢山おられました.
例えばMATLABのinterpftがあります.その関数の説明を引用します.
y = interpft(X,n) は X の関数値のフーリエ変換を内挿し、等間隔に配置された n 個の点を生成します。interpft はサイズが 1 ではない最初の次元で動作します。
FFTを使用した補間法ですが,FFTを使用した微分の関数は用意されていないようです.
プログラム
元の離散信号をFFTしてフーリエ係数を求め,直交基底の線形結合として表現することで補間します.またその微分も容易に求まりますね.
import numpy as np
def fft_interpolate(fs, amp_array, time_array, k=0):
"""
元の離散信号をFFTしてフーリエ係数を求め,直交基底の線形結合として表現することで補間する.
また,その線形結合の微分も容易に求まる.
----------
## Parameters
fs : float
サンプリングレート Hz
amp_array : numpy array
もとの信号
time_array : numpy array
補間したい時間配列
k : int
微分係数
----------
## returuns
amp_array_interp : numpy array
補間した振幅
"""
N = len(amp_array)
freq_array = np.fft.rfftfreq(N,d=1/fs)
fft_amp_array = 2.0 / N * np.fft.rfft(amp_array) #N//2までFFT
fft_amp_array[0] = fft_amp_array[0]/2.0
fft_amp_array = 1j**k * fft_amp_array #微分する
an = np.real(fft_amp_array)
bn = - np.imag(fft_amp_array)
N_2 = len(freq_array) #N//2
amp_array_interp = np.zeros_like(time_array,dtype=np.float64)
# k回微分すると(2πft)**kがそれぞれの基底にかかる
for i in range(N_2):
amp_array_interp += (2*np.pi*freq_array[i])**k * (an[i] * np.cos(2*np.pi*freq_array[i]*time_array) \
+ bn[i] * np.sin(2*np.pi*freq_array[i]*time_array))
return amp_array_interp
結果
1. 試験信号
簡単な三角関数の和を試験信号として使います.その信号の一階,二階微分も計算しておきます.
N = 8192
fs =200.0 #サンプリングレート[Hz]
t = np.arange(start=0.0, stop=N/fs, step=1.0/fs) #時間軸
test_signal = np.cos(2*np.pi*21.0*t) \
+ np.cos(2*np.pi*52.0*t) + np.cos(2*np.pi*70.0*t)
test_grad1 = - 2*np.pi*21.0*np.sin(2*np.pi*21.0*t) \
- 2*np.pi*52.0*np.sin(2*np.pi*52.0*t) - 2*np.pi*70.0* np.sin(2*np.pi*70.0*t)
test_grad2 = - (2*np.pi*21.0)**2 * np.cos(2*np.pi*21.0*t) \
- (2*np.pi*52.0)**2 * np.cos(2*np.pi*52.0*t) - (2*np.pi*70.0)**2 * np.cos(2*np.pi*70.0*t)
2. 補間
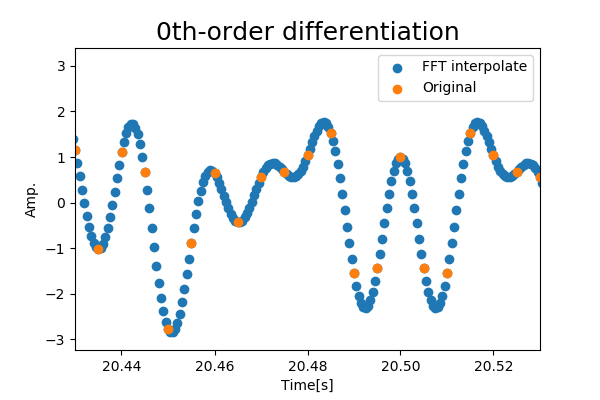
1. 補間(0階微分)
まずは,元の離散信号を補間してみます.
time_array = np.arange(start=0.0, stop=N/fs, step=1.0/fs/10.0)
amp_array = fft_interpolate(fs, test_signal, time_array)
きれいに補間できているように見えます.
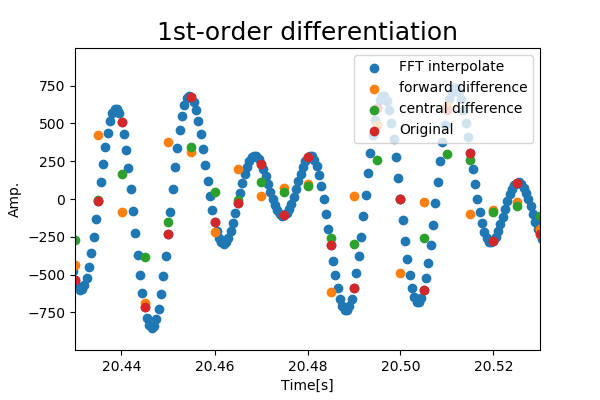
2. 補間(1階微分)
離散信号の一階微分を補間してみます.前進差分,中心差分とも比較してみます.
amp_grad1_array = fft_interpolate(fs, test_signal, time_array, k=1)
forward_diff1 = np.append(np.diff(test_signal)*fs, 0.0) #前進差分.要素数を保つため,末尾に0.0を追加
central_diff1 = np.gradient(test_signal)*fs # 中心差分.要素数を保つため,最初と最後は前進・後退差分
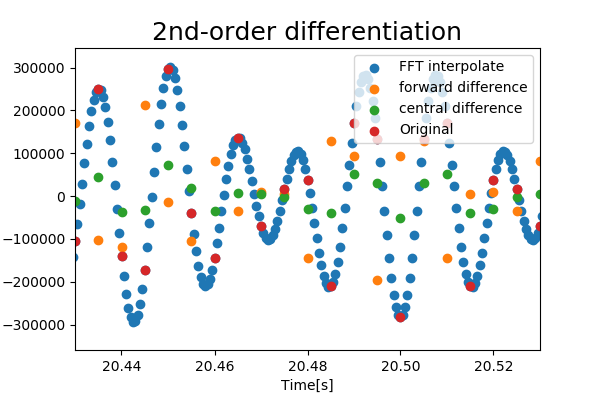
3. 補間(2階微分)
離散信号の一階微分を補間してみます.前進差分を2回,中心差分を2回行ったものとも比較してみます.
amp_grad2_array = fft_interpolate(fs, test_signal, time_array, k=2)
forward_diff2 = np.append(np.diff(forward_diff1)*fs, 0.0) #前進差分.要素数を保つため,末尾に0.0を追加
central_diff2 = np.gradient(central_diff1)*fs # 中心差分.要素数を保つため,最初と最後は前進・後退差分
3. 誤差の評価
FFTを用いた微分,前進差分,中心差分の誤差を求めます.誤差は,
(誤差) = {(数値微分値) - (理論値)} / (理論値の標準偏差)
としました.
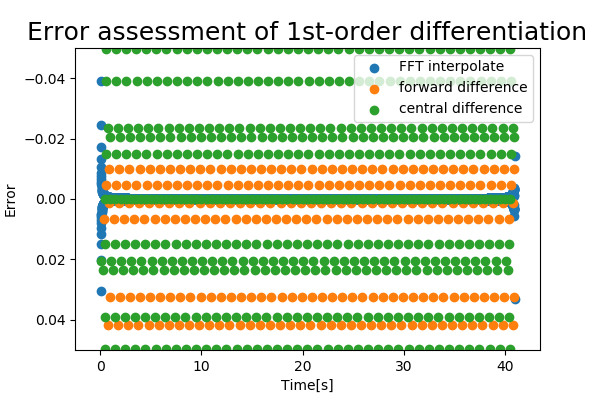
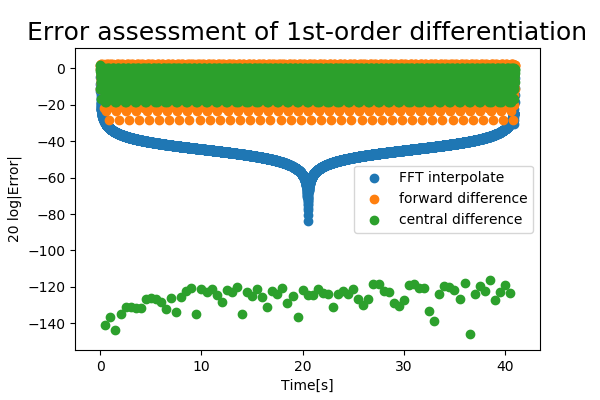
1. 1階微分
interpolate_1 = fft_interpolate(fs, test_signal, t, k=1) #一階微分補間
fft_error1 = (interpolate_1 - test_grad1) / np.std(test_grad1)
fd_error1 = (forward_diff1 - test_grad1) / np.std(test_grad1)
cd_error1 = (central_diff1 - test_grad1) / np.std(test_grad1)
FFTを用いた微分法は概ね精度良く微分値が求められているようですが,信号の両端は悪いです.
FFTの窓関数として今回は矩形窓を使用しているので,このようになっているのでしょうか.
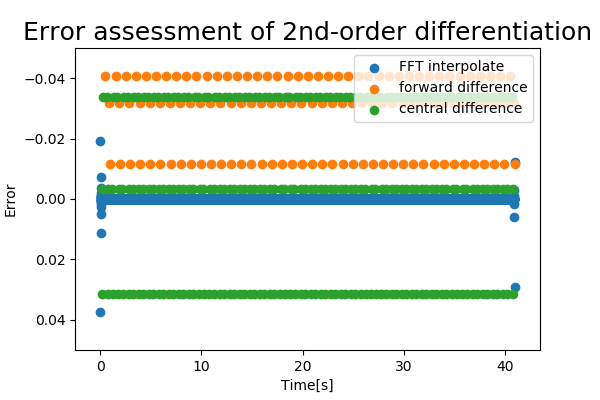
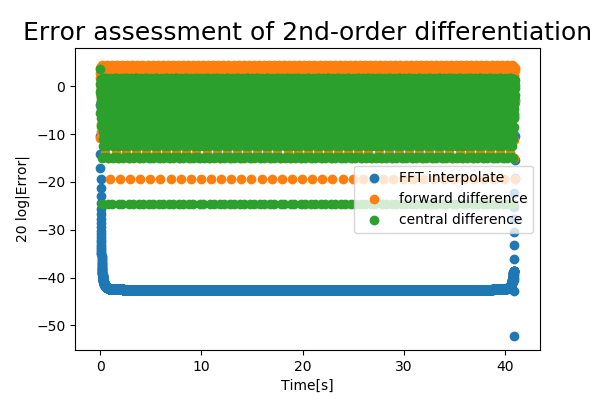
2. 2階微分
interpolate_2 = fft_interpolate(fs, test_signal, t, k=2) #一階微分補間
fft_error2 = (interpolate_2 - test_grad2) / np.std(test_grad2)
fd_error2 = (forward_diff2 - test_grad2) / np.std(test_grad2)
cd_error2 = (central_diff2 - test_grad2) / np.std(test_grad2)
まとめ
FFTを用いて離散信号のフーリエ係数を求め,直交基底の線形結合として表現することで補間と微分が行えることを示しました.
解析的に誤差を評価したわけではなく,おおざっぱな評価で申し訳ありませんが,そのFFTを用いた微分は前進差分や中心差分と比べ,部分的には良い精度を与えることがわかりました.
何かの役に立てば幸いです.