はじめに

　混ざった信号を分離する方法として、独立成分分析があります。
例えば、音源が3つあったとして、それらの混ざり具合の異なる信号が3つあれば分離できる場合があります。
ブラインド音源分離と呼ばれる分野です。
　ブラインド音源分離をやって見る前に、数学的な理論は置いておいて、独立成分分析の手順をグラフを書きながら学びたいと思います。

この投稿の大まかな流れは次の通りです。

主成分分析無相関化の話
中心極限定理どんな分布も足すとガウス分布になる話
独立成分分析非ガウス性を最大化するように変換する話

参考

独立成分解析の信号処理への応用

データ化学工学研究室独立成分分析 (Independent Component Analysis, ICA) ～PCAの無相関より強力な ”独立” な成分を抽出～

使用するモジュールと関数

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
from sklearn.decomposition import FastICA

円を描くときに使います。

def circle(n,r=1):
    rad = np.linspace(0.0,2.0*np.pi,n)
    return np.asarray([np.cos(rad),np.sin(rad)]).T

データを回転させるときに使います。

def rotation_matrix(rad):
    return np.array([[np.cos(rad),-np.sin(rad)],[np.sin(rad),np.cos(rad)]])

独立成分分析

　無相関、独立という言葉はあまり日常では馴染みがありません。
数学で言う無相関とは、何の関係もないという意味ではなく、変数間に線形な関係がないことを表します。
非線形な関係があっても線形な関係がなければ無相関です。
独立は、無相関より厳しい条件です。非線形な関係もない状態を指します。
独立であるなら無相関となります。

独立な成分を抜き出したいのですが、独立であるなら無相関なので、まずは無相関化を行います。

無相関化(主成分分析)

　細かい導出はしませんが、データが多変量正規分布に従うとして、その分散共分散行列を対角化することを目指すか、基底の貼る空間に射影したときのデータの分散が最大になるような直交基底変換行列を探すことを目指します。
　結果的にはどちらも同じになり、分散共分散行列の固有値・固有ベクトルを求めることになります。

主成分分析の手順は以下のとおりです。

データから平均を引いて平均を0にする
分散共分散行列を計算する
分散共分散行列を固有値分解する

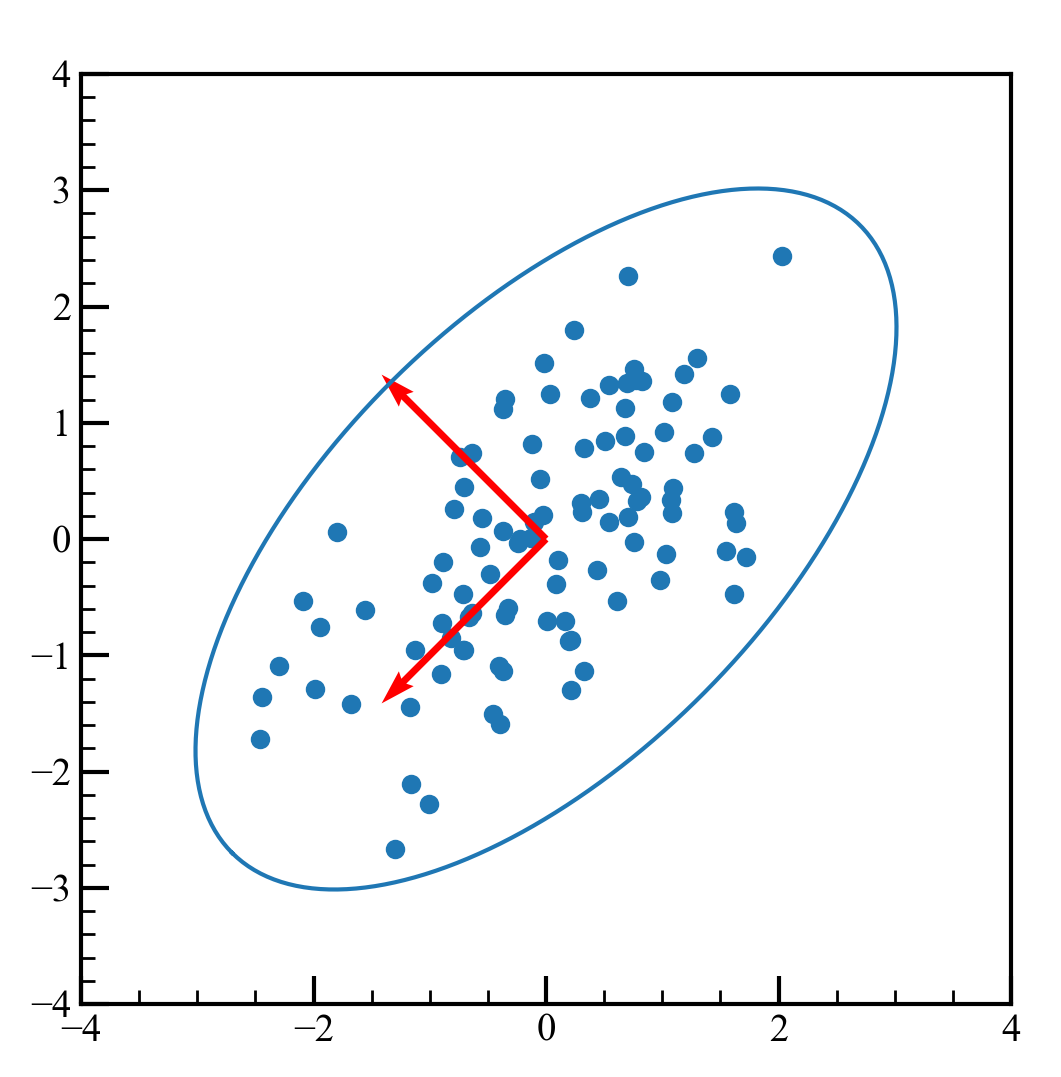
実際に主成分分析を行うと何がどうなるのかグラフで見てみます。
使用するデータは多変量ガウス分布です。

np.random.seed(0)
mean = np.array([0.0, 0.0])
cov = np.array([[1.0, 0.6], [0.6, 1.0]])
data = np.random.multivariate_normal(mean, cov, size=100)

主成分分析を行います。

data = data - np.mean(data,axis=0) #各次元の平均を0にする
cov = np.cov(data, rowvar=False) #分散共分散行列
u,w,_ = np.linalg.svd(cov) #固有値分解 uが固有ベクトル wが固有値 基底変換後のcovの対角になる

#分散共分散行列の楕円を描く　確率長円と違って大きさは適当
c = circle(200,r=1.0)
c = c*np.sqrt(w) #楕円にする
c = c.dot(u) #回転させる

fig,axes = plt.subplots(figsize=(6,8))
axes.scatter(data.T[0],data.T[1])
axes.quiver(0,0,u[0,0],u[0,1],color = "red",angles = "xy", scale_units = "xy",scale = 0.5)
axes.quiver(0,0,u[1,0],u[1,1],color = "red",angles = "xy", scale_units = "xy",scale = 0.5)
axes.plot(c.T[0]*3,c.T[1]*3)
axes.set_aspect("equal")
axes.set_ylim(-4.0,4.0)
axes.set_xlim(-4.0,4.0)

円は確率長円もどきです。大きさは適当です。

元のデータに分散共分散行列の固有ベクトルをかけて、基底変換します。

pca_data = data.dot(u)　#回転
pca_ax = u.dot(u) #赤い矢印の回転
c = c.dot(u) #楕円の回転

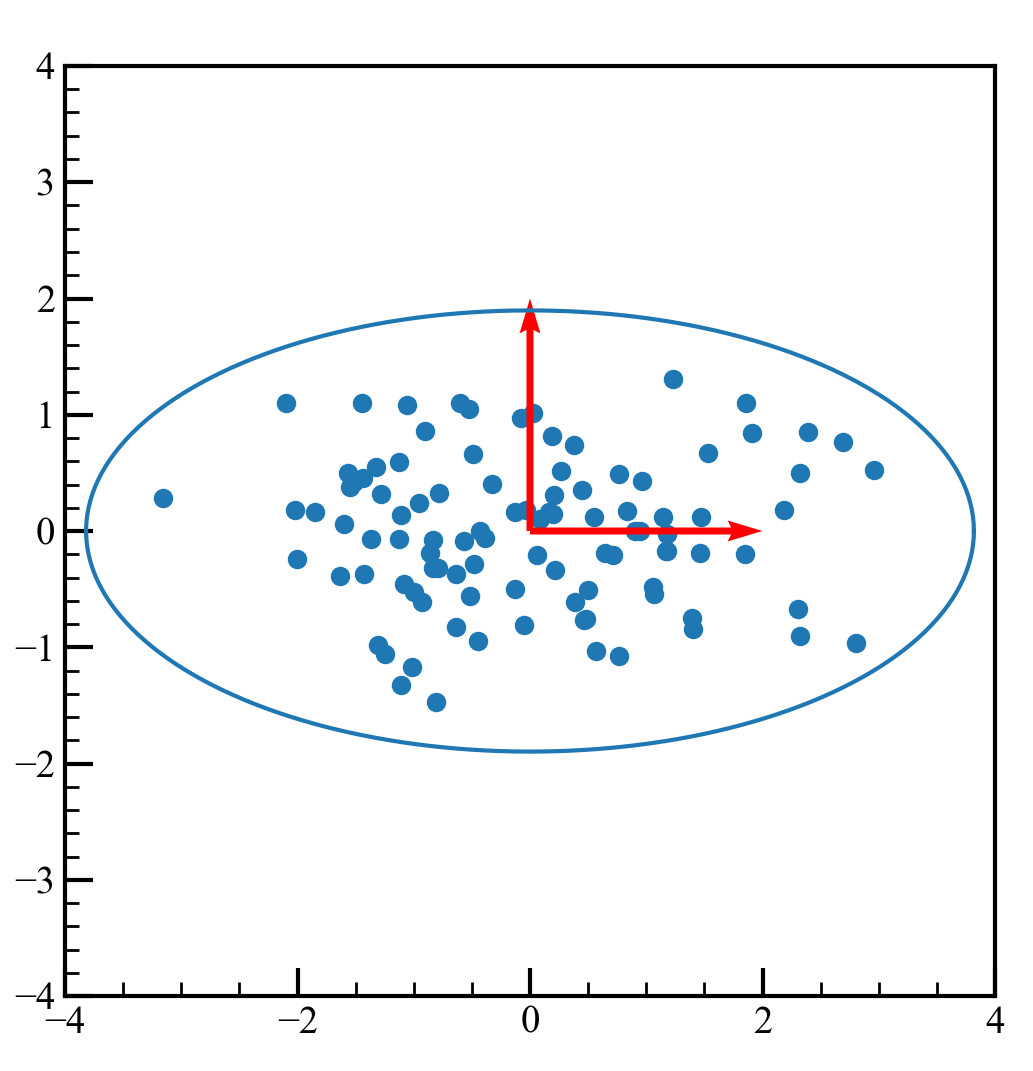
グラフの描画のコードは上とほとんど同じなので省略します。

軸が回転した様子がわかると思います。

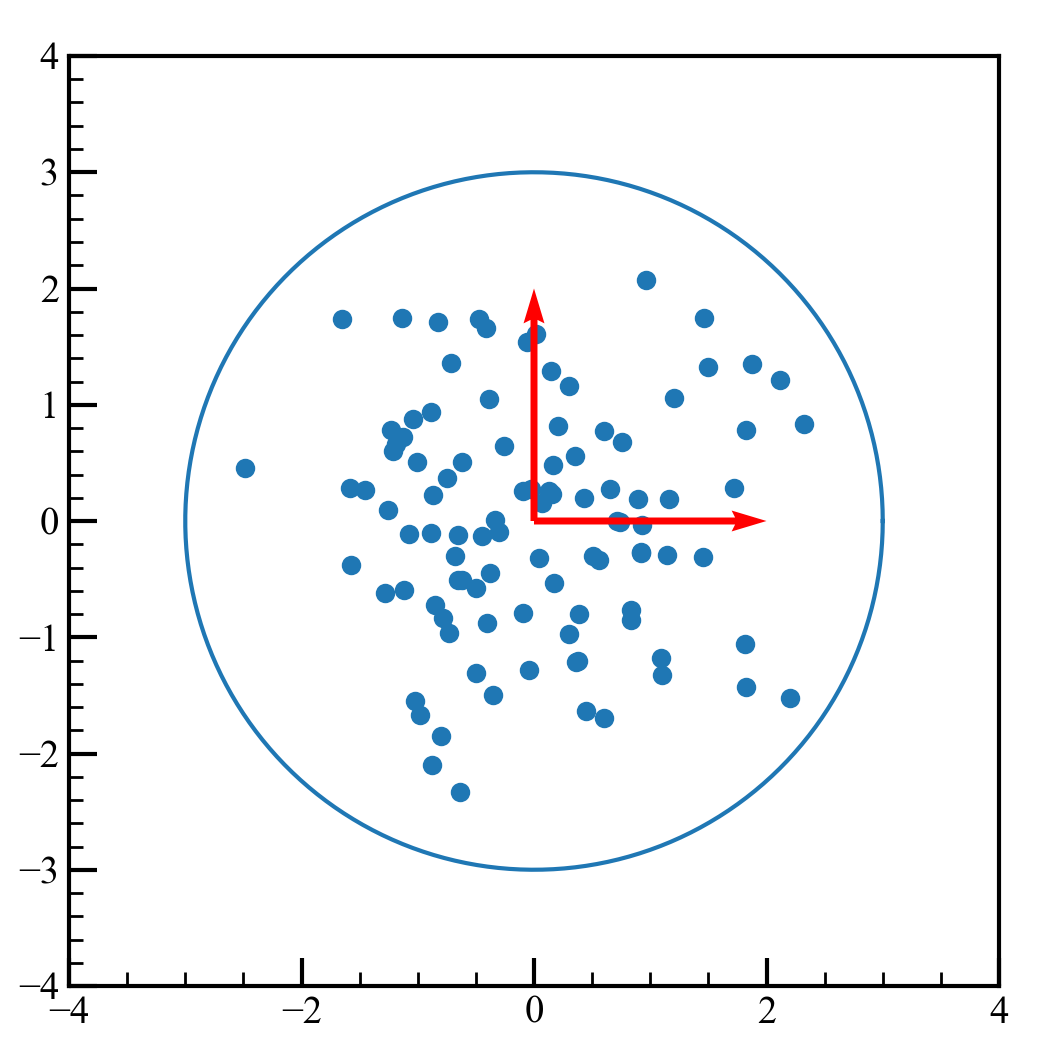
続いて分散共分散行列が単位行列になるように正規化します。
基底変換した後のデータを固有値の平方根で割ります。

norm_pca_data = pca_data/np.sqrt(w) #データの正規化
norm_c = c / np.sqrt(w) #円の正規化

確認のため、このデータの分散共分散行列を計算してみます。

np.cov(norm_pca_data,rowvar=False)

array([[ 1.00000000e+00, -2.14306523e-17],
       [-2.14306523e-17,  1.00000000e+00]])

データを回転させても、分散共分散行列は単位行列のままです。

np.cov(norm_pca_data.dot(rotation_matrix(np.pi/2)),rowvar=False)

array([[1.00000000e+00, 3.23453187e-18],
       [3.23453187e-18, 1.00000000e+00]])

独立成分分析で残ったやることは、この回転だけです。

中心極限定理

どんな分布も足し合わせると正規分布に近づいていきます。
これを中心極限定理と言います。
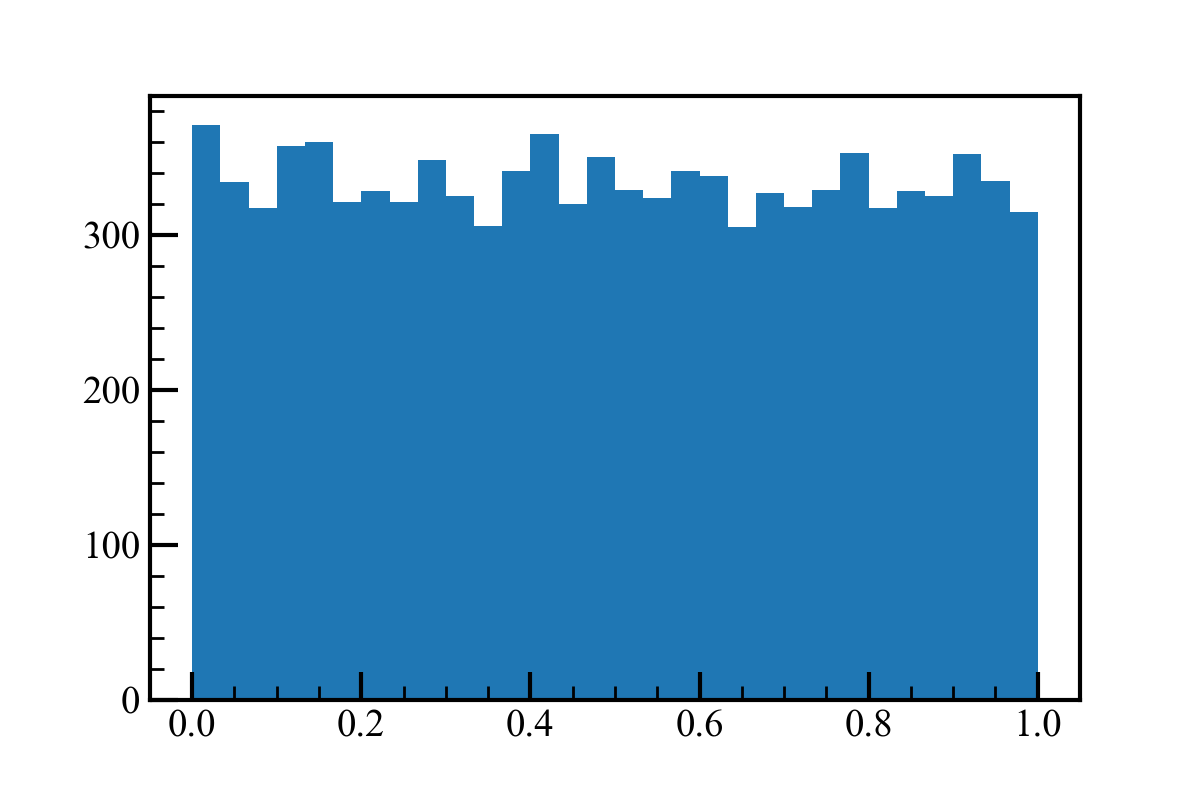
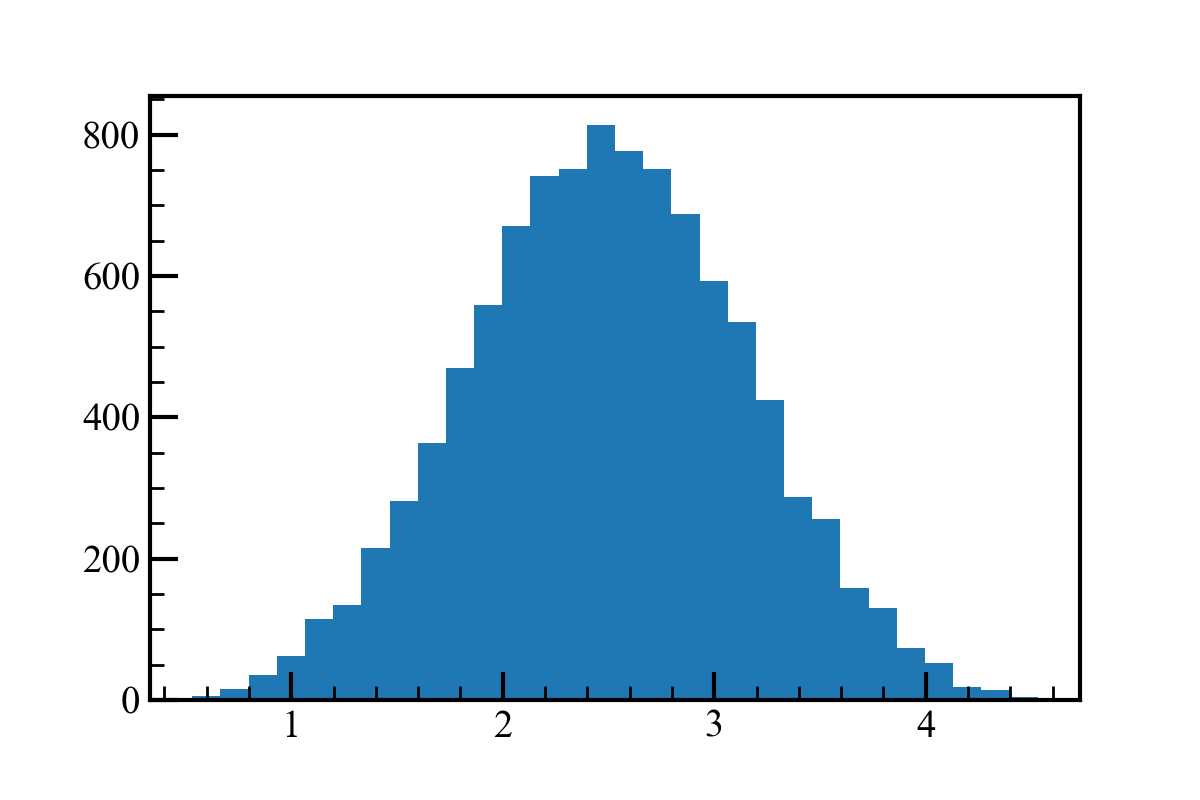
試しに一様分布を足し合わせてみます。

np.random.seed(0)
uni_dist = np.random.random(10000)
uni_dist_5 = np.random.random(10000)+np.random.random(10000)+np.random.random(10000)+np.random.random(10000)+np.random.random(10000)

fig,axes = plt.subplots()
axes.hist(uni_dist,bins=30)

fig,axes = plt.subplots()
axes.hist(uni_dist_5,bins=30)

一様分布も足し合わせるとガウス分布に近づきました。

　独立成分分析では、分離後にガウス分布から離れるように変換を行います。
これは、混ざる前の分布が非ガウス分布であることを仮定しているためです。
　どれくらいガウス分布から離れたかの指標に、ここでは高次統計量の尖度を使います。
尖度は正規分布であれば定数ですが、尖った分布になると値が大きくなります。

　先程は多変量ガウス分布をテストデータに使いましたが、実は主成分分析した時点で独立になってしまうので次は違うデータでやります。

非ガウス性の最大化

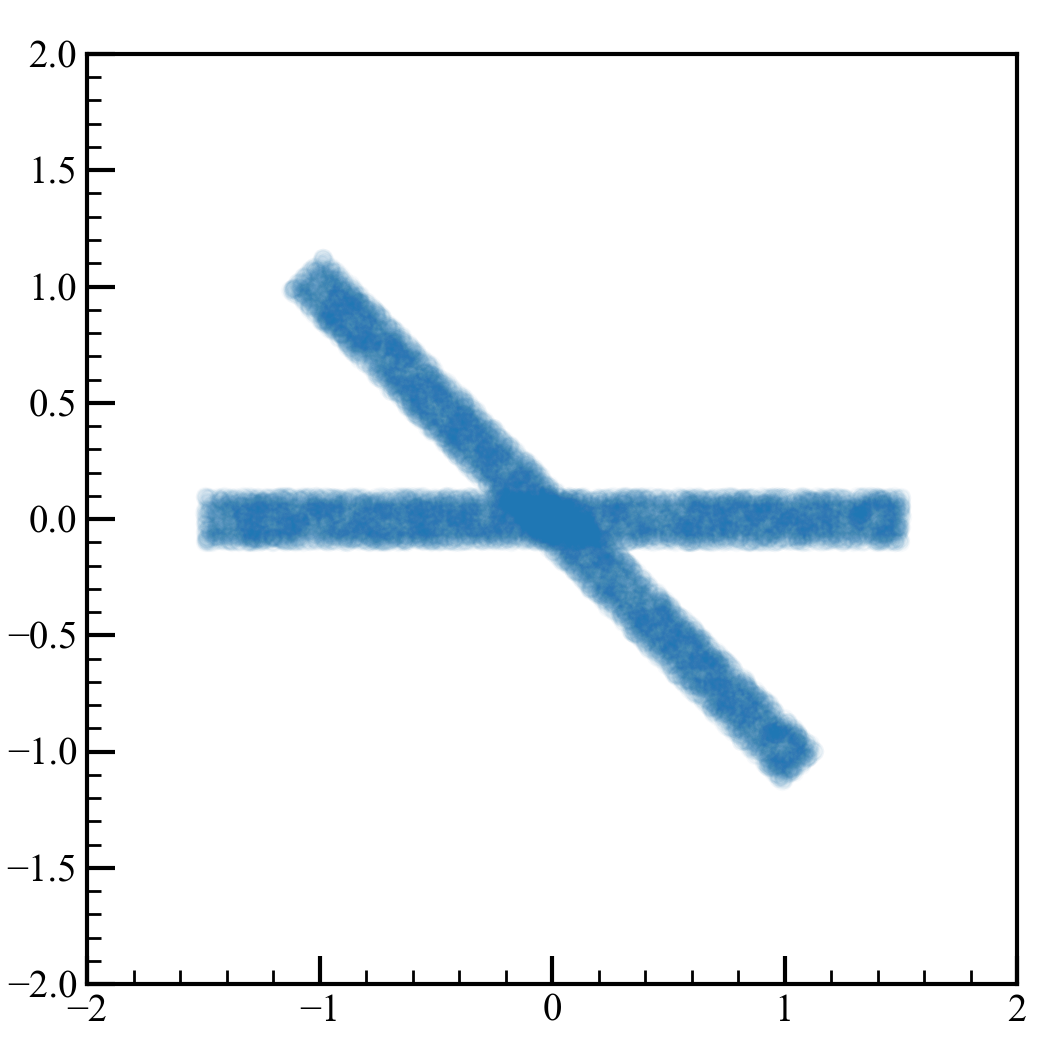
ガウス分布に従わないデータを作ります。

x = 3*np.random.random(5000)
x -= x.mean()
y = 0.2*np.random.random(5000)
y -= y.mean()
data = np.array([x,y]).T
data = np.vstack([data,data.dot(rotation_matrix(np.pi/4))])

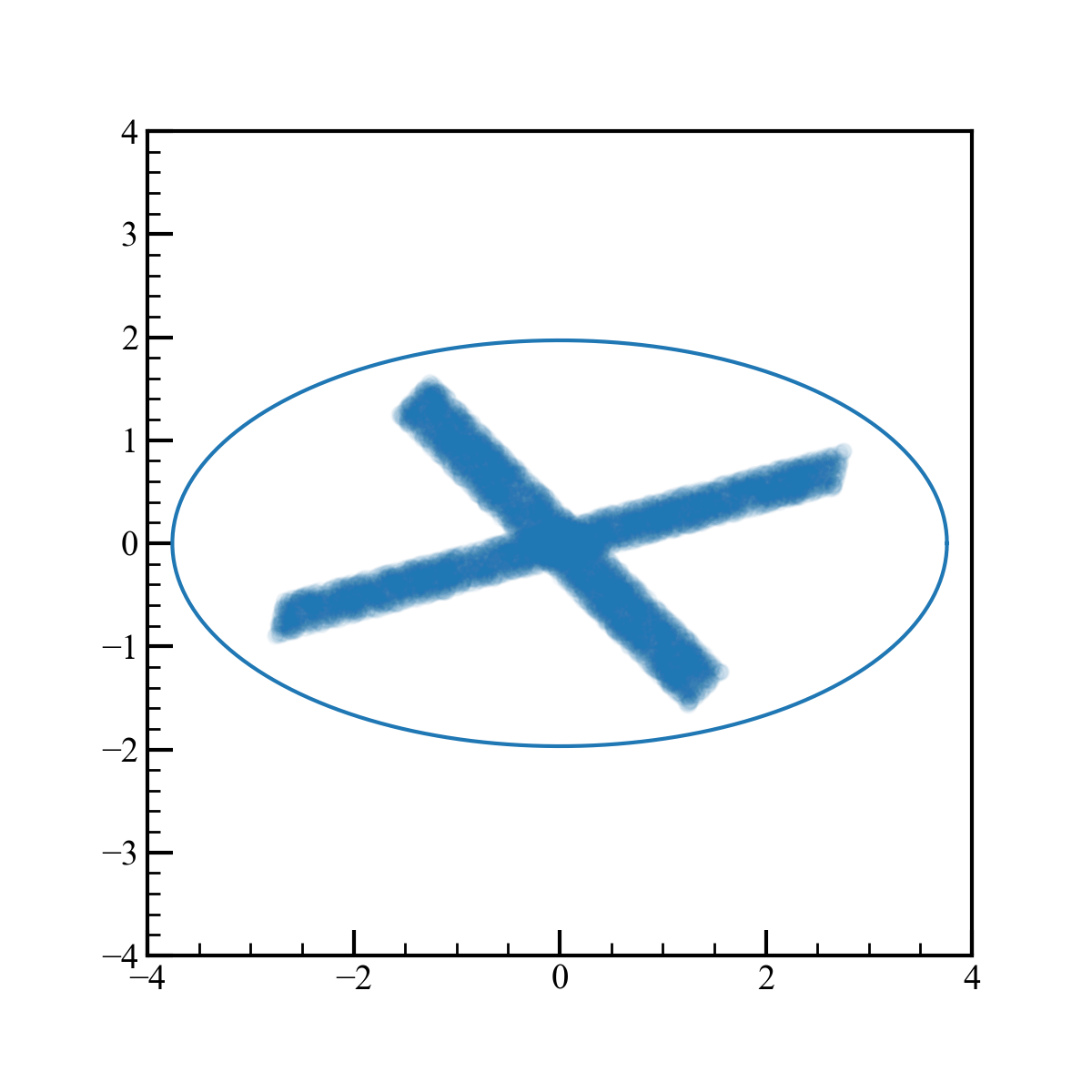
まずは主成分分析して無相関化します。

data = data - np.mean(data,axis=0) #各次元の平均を0にする
cov = np.cov(data, rowvar=False) #分散共分散行列
u,w,_ = np.linalg.svd(cov) #固有値分解

pca_data = data.dot(u) #無相関化

標準偏差が1になるように正規化します。

norm_pca_data = pca_data/np.sqrt(w)

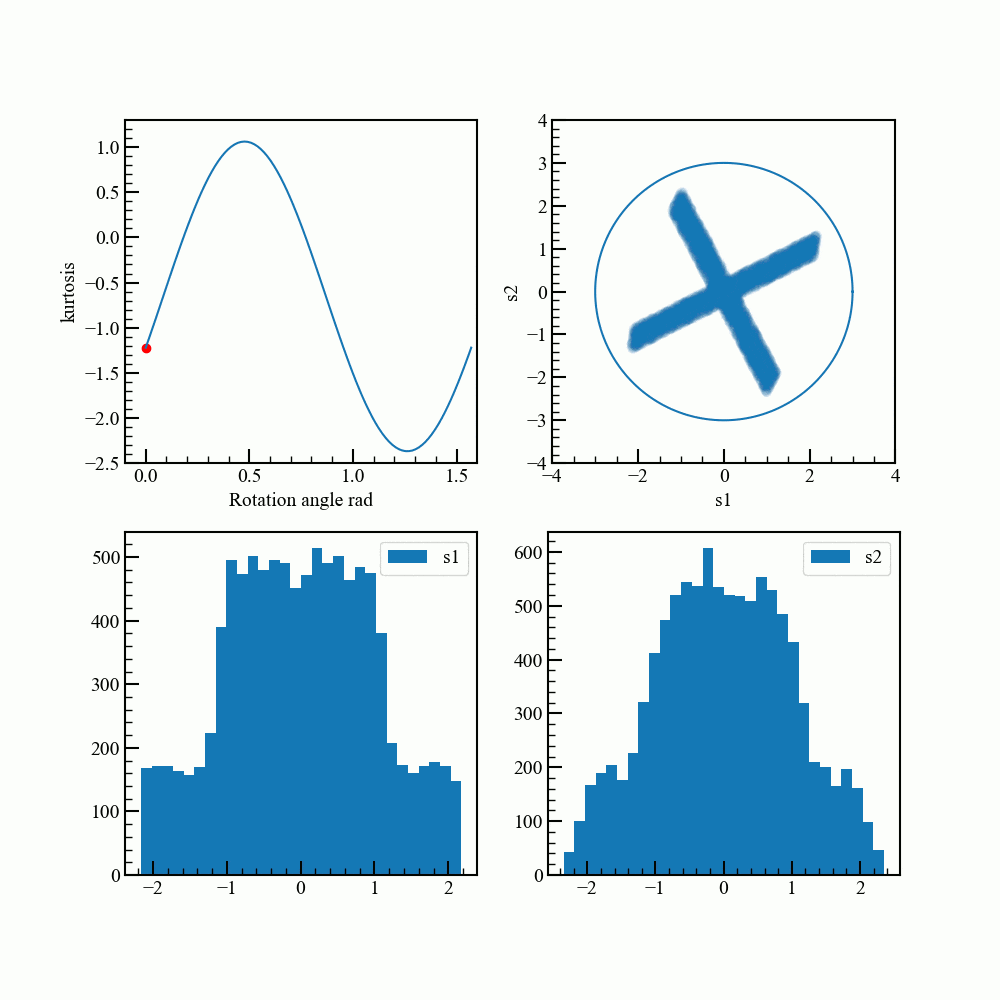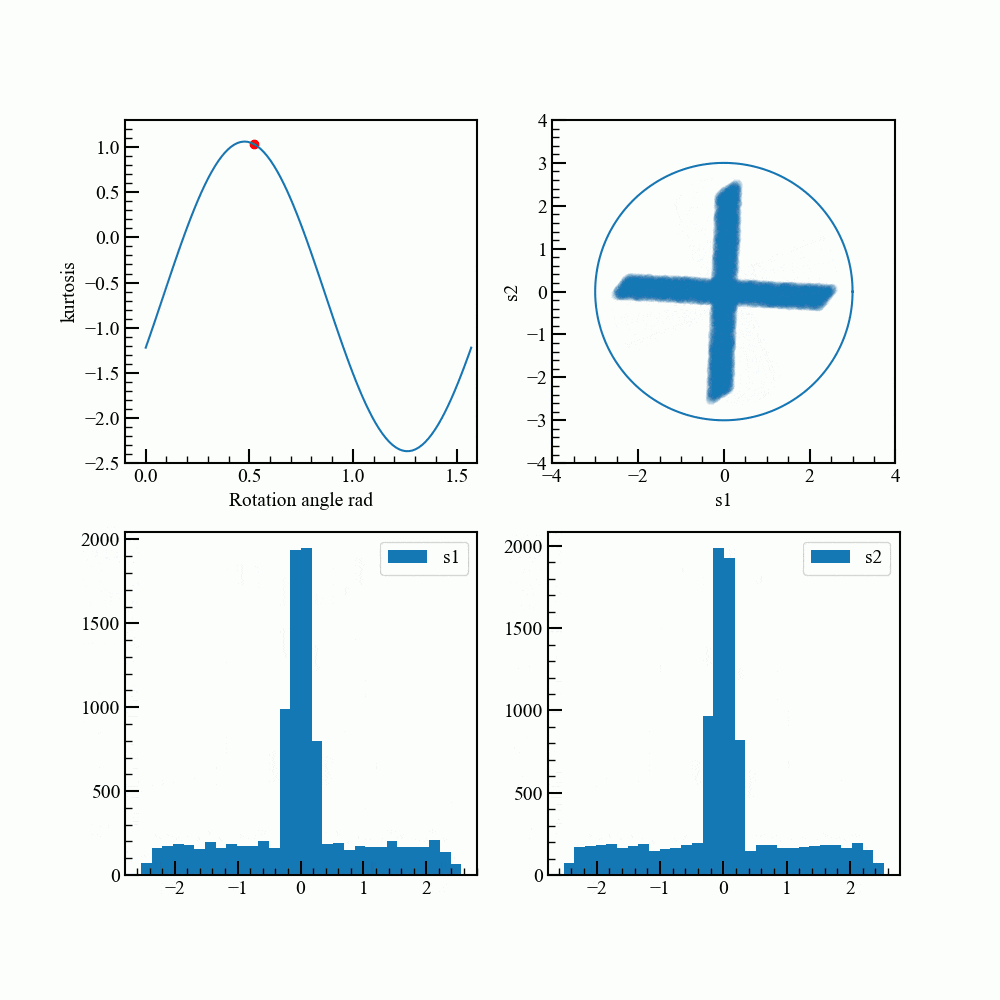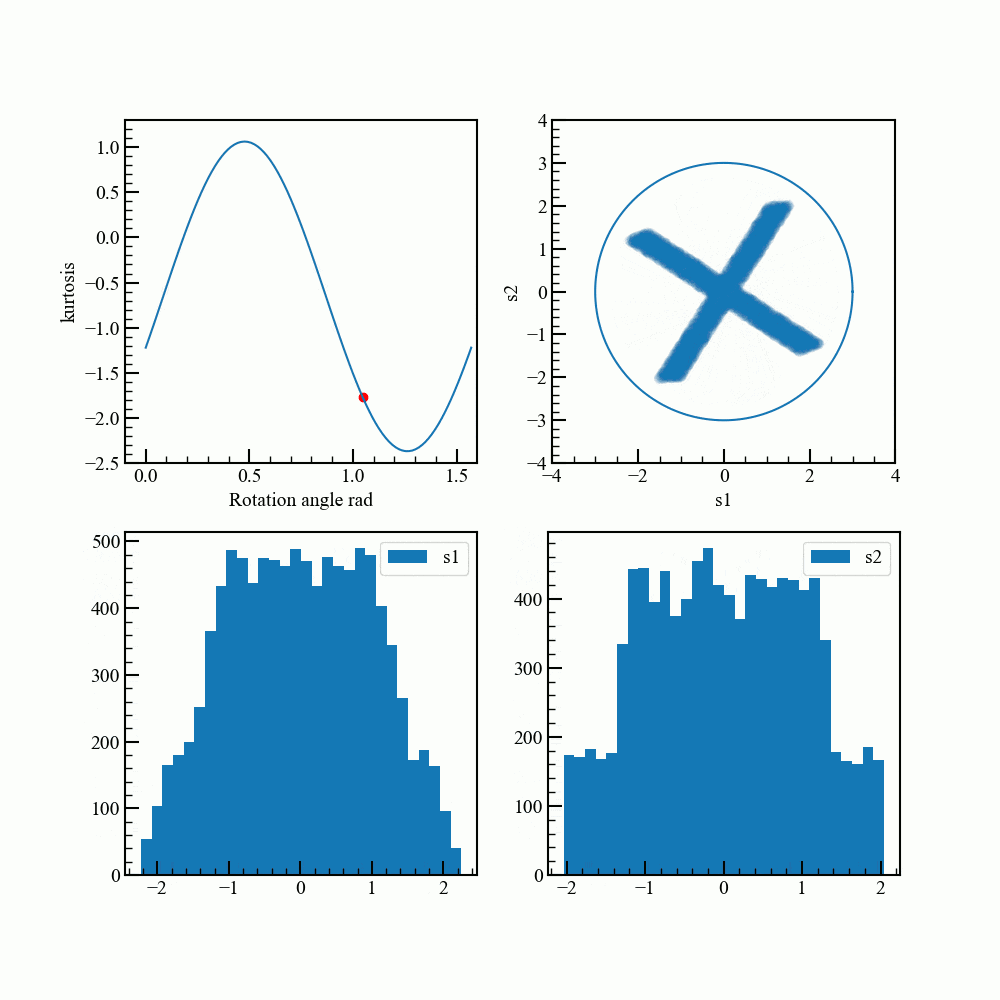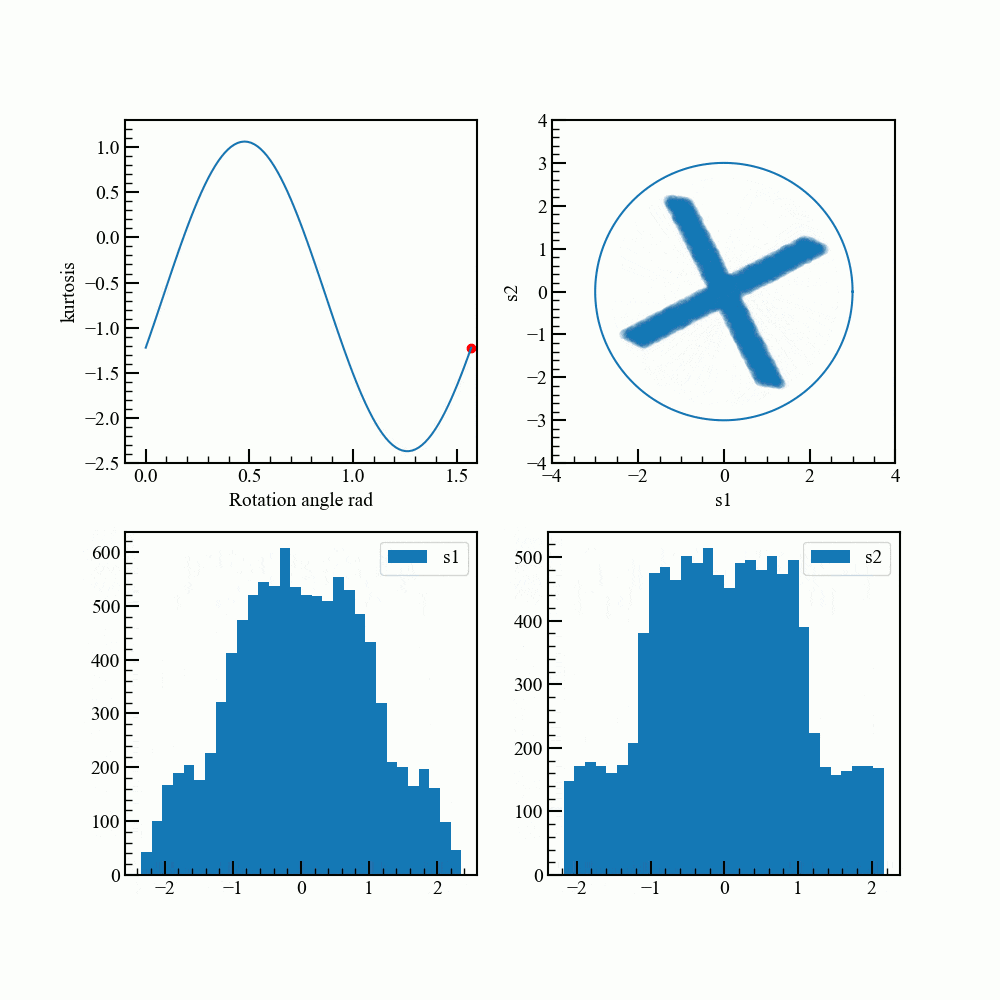
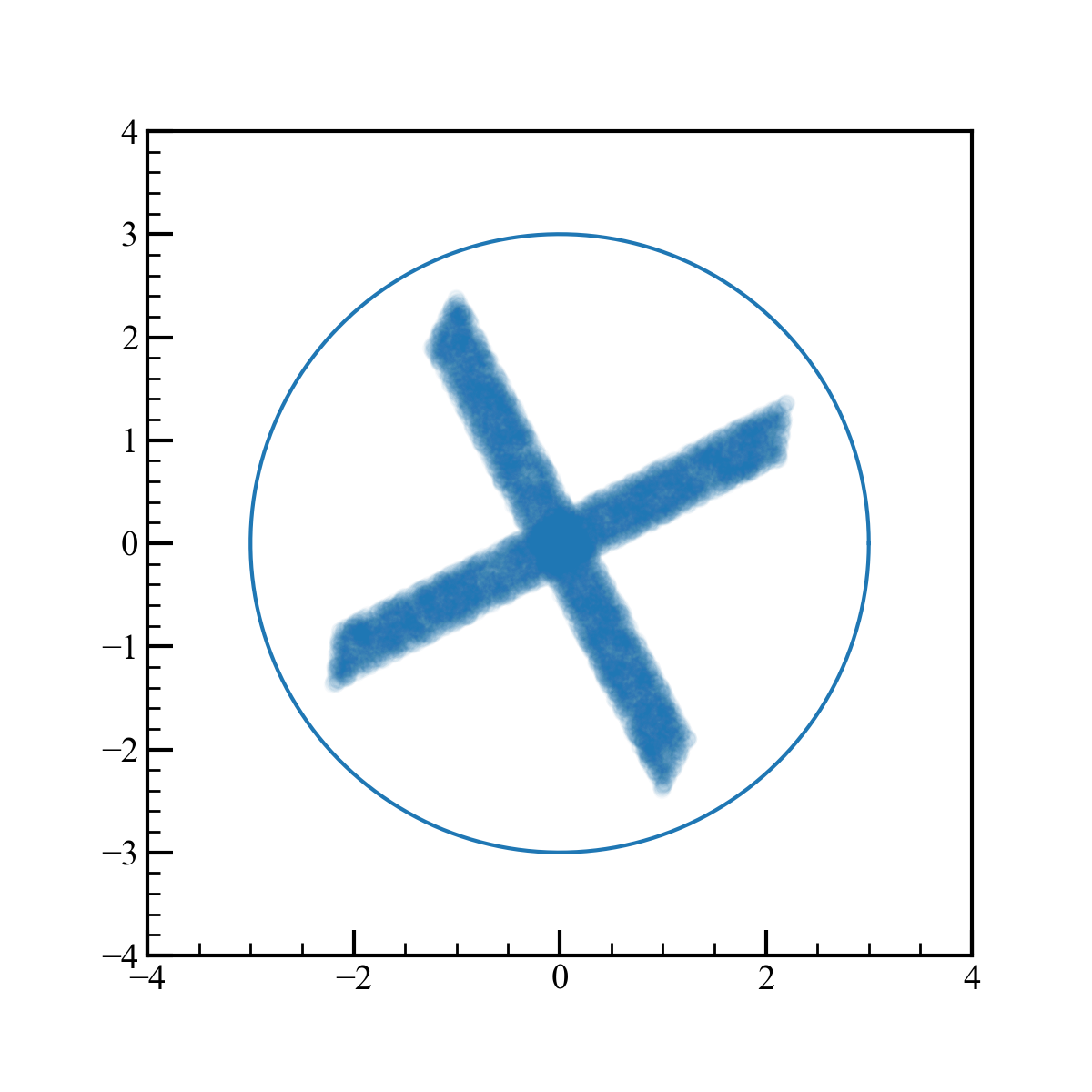
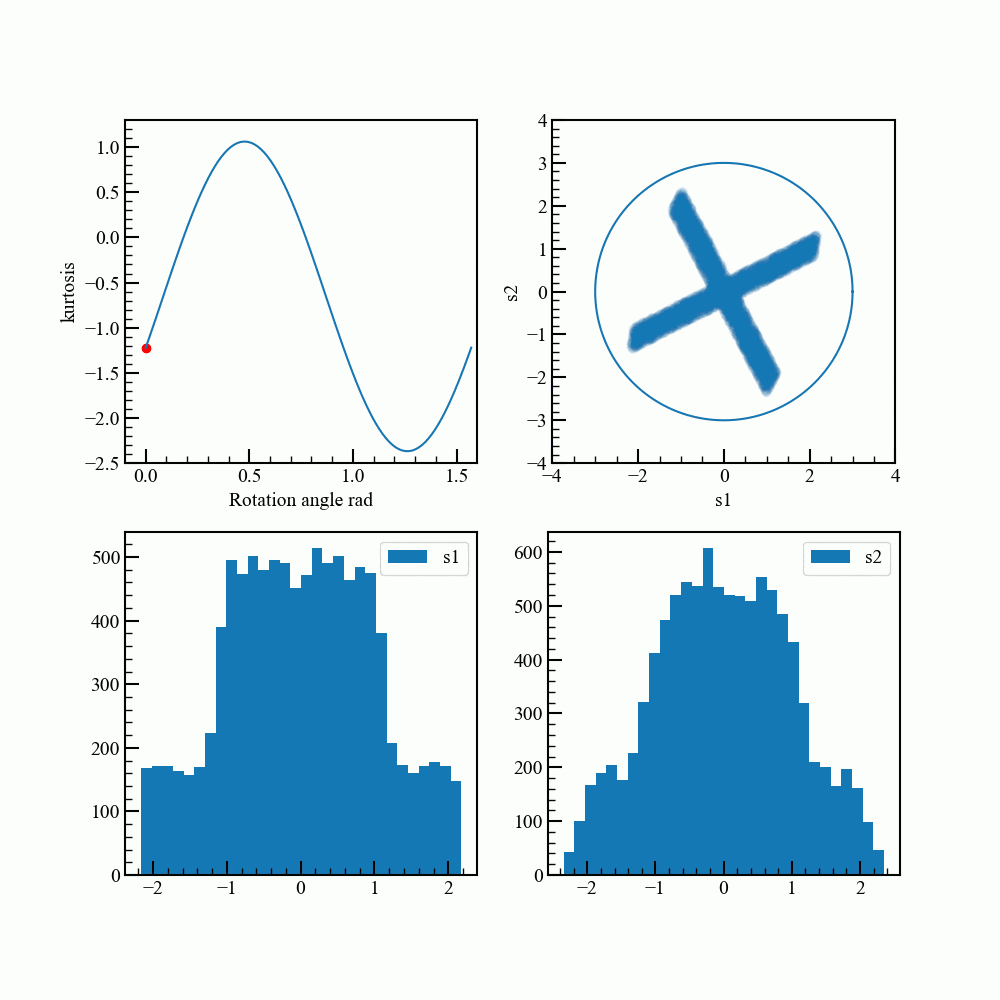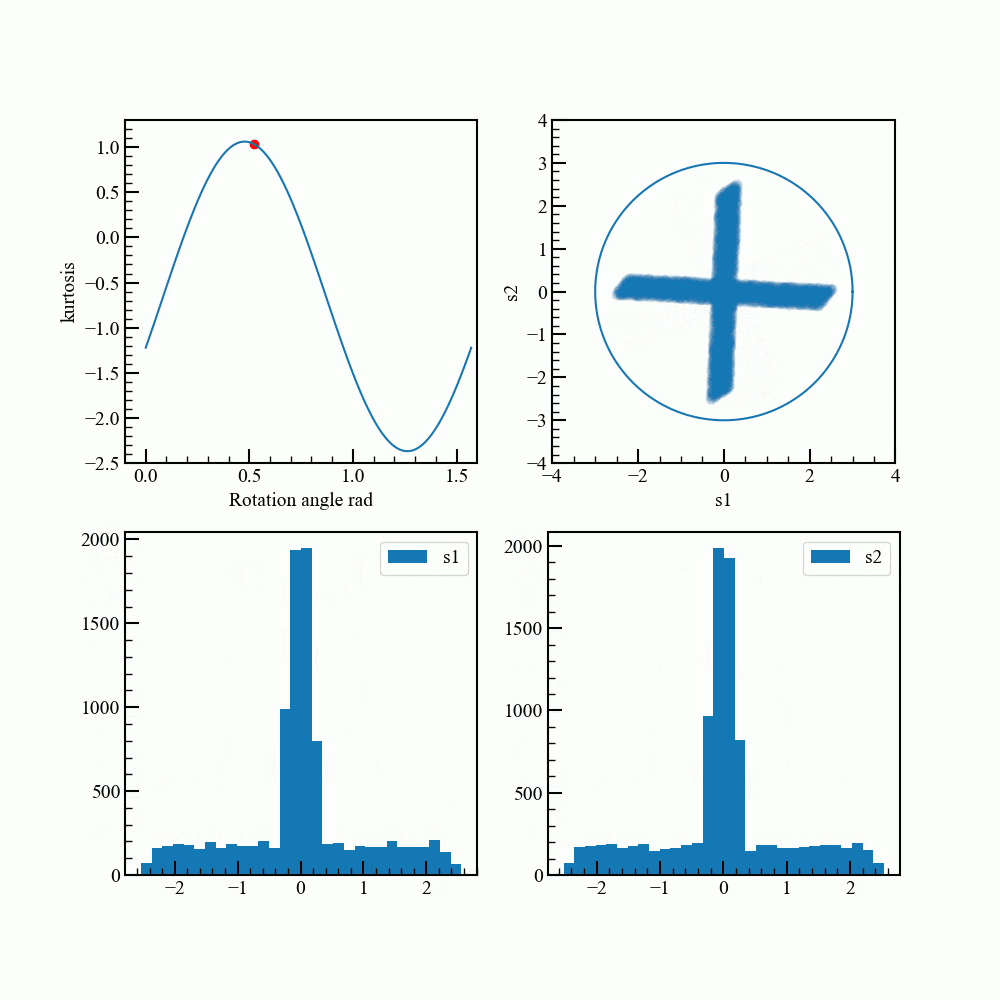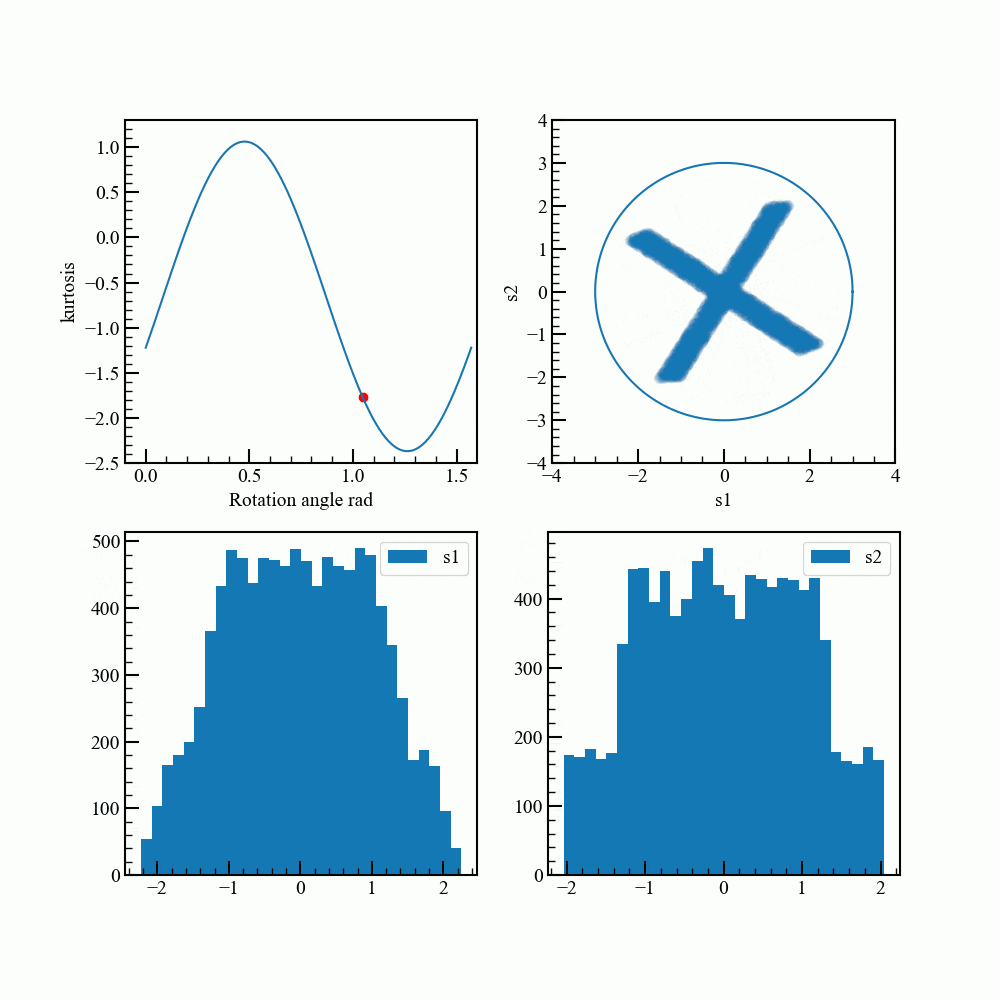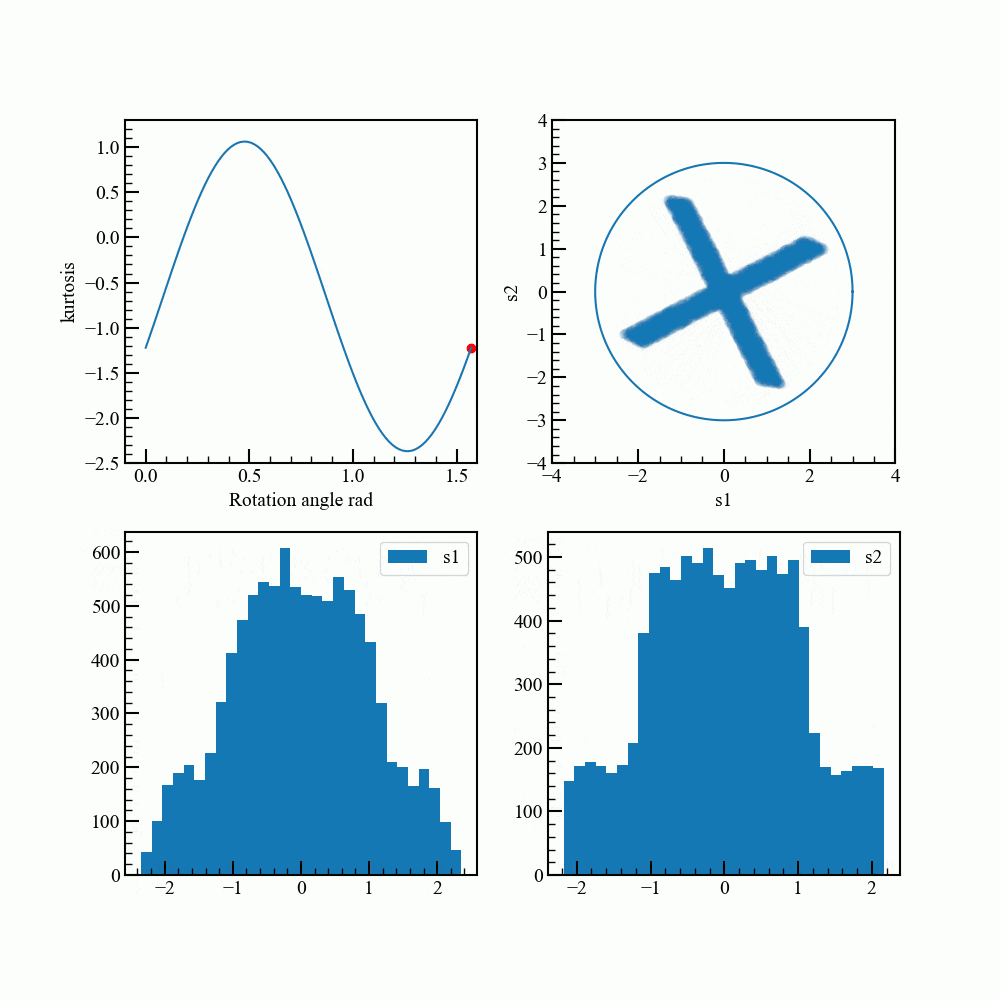
回転させて最もガウス分布から離れる角度を調べます。
通常は勾配法などを使うそうですが、ここでは総当りです。
アニメーションで見てみます。グラフ描画のコードが煩雑になってしまいました。

rad_array = np.linspace(0.0,np.pi/2.0,100)

kurt_array = []
for rad in rad_array:
    rot_data = norm_pca_data.dot(rotation_matrix(rad))
    kurt = np.sum(stats.kurtosis(rot_data))
    kurt_array.append(kurt)

for i,rad in enumerate(rad_array):
    rot_data = norm_pca_data.dot(rotation_matrix(rad))
    kurt = np.sum(stats.kurtosis(rot_data))

    fig = plt.figure(figsize=(10,10))
    ax1,ax2,ax3,ax4 = fig.add_subplot(2,2,1),fig.add_subplot(2,2,2),fig.add_subplot(2,2,3),fig.add_subplot(2,2,4)

    ax1.plot(rad_array,kurt_array)
    ax1.scatter(rad,kurt,color="red")
    ax1.set_xlabel("Rotation angle rad")
    ax1.set_xlim(-0.1,1.6)
    ax1.set_ylim(-2.5,1.3)

    ax2.scatter(rot_data.T[0],rot_data.T[1],alpha=0.03) #元データ回転
    ax2.plot(c.T[0]*3,c.T[1]*3)
    ax2.set_aspect("equal")
    ax2.set_ylim(-4.0,4.0)
    ax2.set_xlim(-4.0,4.0)
    ax2.set_xlabel("s1")
    ax2.set_ylabel("s2")

    ax3.hist(rot_data.T[0],bins=30,label="s1")
    ax4.hist(rot_data.T[1],bins=30,label="s2")

    ax3.legend(loc="upper right")
    ax4.legend(loc="upper right")

    ax1.set_ylabel("kurtosis")
    fig.savefig("{}.png".format(i),dpi=100)
    plt.close()

尖度が最大になったときのデータはこれです。

合っているのか確認のためsklearnのFastICAでも独立成分分析を行ってみます。

decomposer = FastICA(n_components = 2)
decomposer.fit(data)
S = decomposer.transform(data)

fig,axes = plt.subplots(figsize=(6,6))
axes.scatter(S.T[0],S.T[1],alpha=0.1)
axes.set_aspect("equal")

絶対値は同じになりませんが、見た目は同じです。問題なさそうです。

まとめ

独立成分分析は、無相関化、正規化、非ガウス性の最大化の順に行えば良いことがわかりました。
次は音声信号で試してみたいと思います。

グラフで理解する独立成分分析