線形補間による不等間隔データのフーリエ変換

時系列データは普通，時間的に等間隔にサンプリングされている，あるいは，誤差の範囲でそう見なせることが多い．
等間隔データに対する数値フーリエ変換を行うには高速フーリエ変換アルゴリズム(FFT)を利用する．
しかし，等間隔でないデータに，FFTを用いることは難しい．

そういった場合にフーリエ変換を行いたい場合のサンプルケースとして，ここでは線形補間を用いた積分計算の方法を紹介する．

間違いあればご指摘ください．

問題設定

等間隔でないサンプリングを$N$点，時刻$t_1,t_2,\ldots,t_N$で行い，
時系列データ$f(t_1),f(t_2),\ldots,f(t_N)$を得たとする．
次式のフーリエ変換$\mathcal{F}$において，ある角周波数$\omega$に対する右辺の積分を，この時系列データを用いて評価したい．

\hat{f}(\omega)=\mathcal{F}[f(t)](\omega)=\int^\infty_{-\infty} f(t) e^{-i\omega t}{\rm d}t

方法

所望の角周波数で線形補間による数値フーリエ変換ができる．
式変形は後ろを見てください．

\begin{aligned}
    &\sum_{k=1}^{N-1}\int^{t_{k+1}}_{t_k} f(t) e^{-i\omega t}{\rm d}t\\
    &=\sum_{k=1}^{N-1}f(t_k)e^{-i\omega t_k} C+ f(t_{k+1})e^{-i\omega t_{k+1}}\overline{C}\\
    &where,\quad C=\frac{1-i\omega(t_{k+1}-t_k)-e^{-i\omega(t_{k+1}-t_k)}}{\omega^2(t_{k+1}-t_k)}     
\end{aligned}

実装

Pythonでの実装例を示す．　Matlabとかだと似たようなライブラリがあるらしい．

def dft(w,t,G):
    def expi(x):
        return np.exp(complex(0.,x))
    res = 0.+0.j
    for i in range(len(t)-1):
        tx,ty = t[i],t[i+1]
        Gx,Gy = G[i],G[i+1]
        dt = ty-tx
        exwdt = expi(-w*dt)
        d = (complex(1.0,-w*dt) - exwdt )/(w**2*dt)
        dc= d.conjugate()                
        res += (Gx*d + Gy*dc * exwdt) * expi(-w*tx)
    return w, res.real, res.imag

例

$f(t)=\exp(-t)$の関数から時刻$t=t_1,2^1t_1,\ldots,2^{N-1}t_1$のように$N=20$点サンプルする．

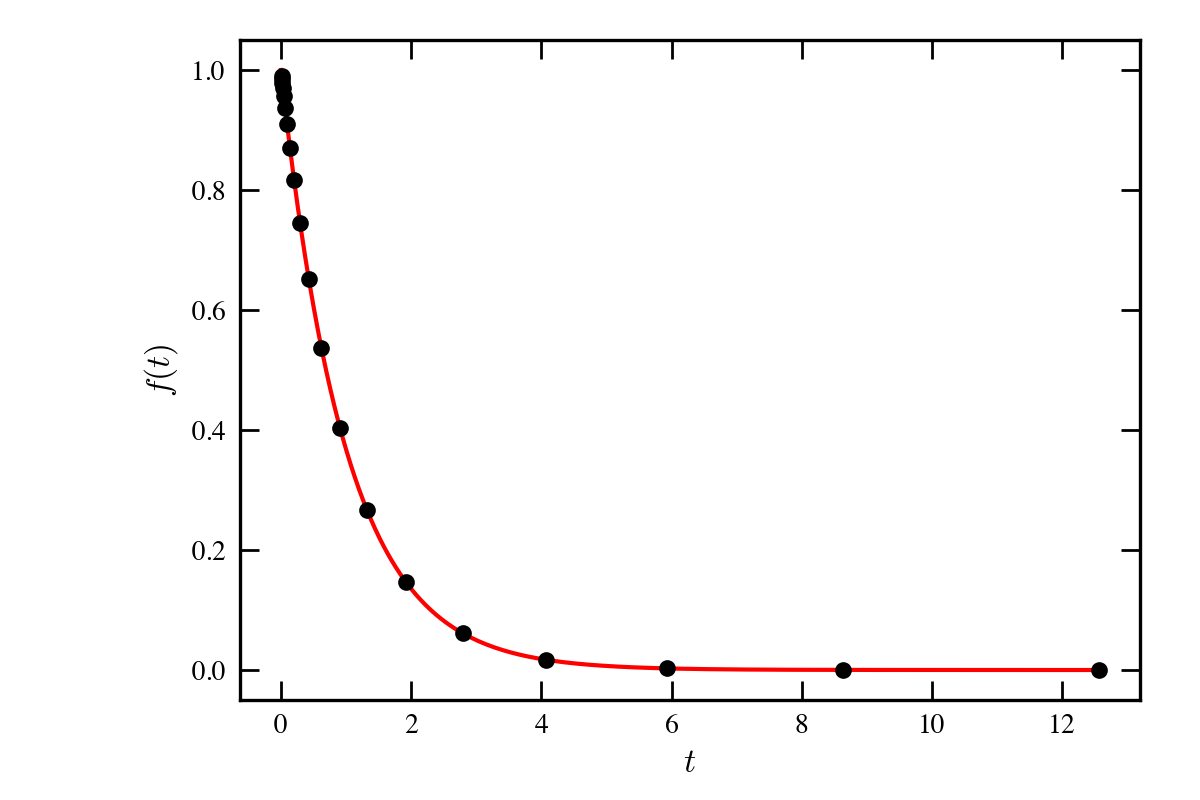
次式の関係を，フーリエ変換を用いて確認する． 前処理としてhann窓関数を用いた．
$$
i\omega\int^{\infty}_0e^{-t}e^{i\omega t}{\rm d}t
=\frac{\omega^2}{1+\omega^2}+i\frac{\omega}{1+\omega^2}
$$
図の黒線は右辺の解析解で，シンボルは数値解である．

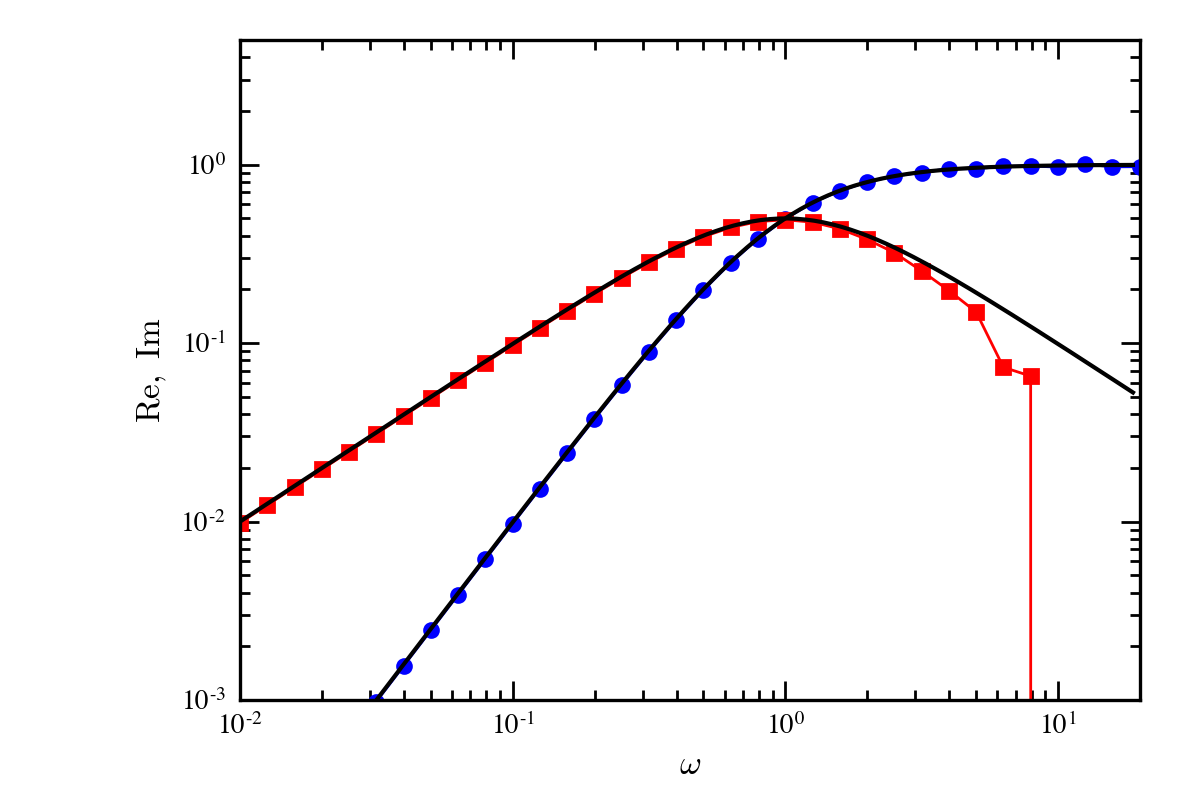
高周波領域で乱れるが，20点程度でもかなり良い精度になることが確認できる．

詳細：線形補間を用いた定積分

隣あった２点間$[t_x,t_y]$において，$f(t)$を線形補間する．

f(t)=f(t_x)+(t-t_x)\frac{f(t_y)-f(t_x)}{t_y-t_x}

このとき区間$[t_x,t_y]$で，求める積分が解析的に評価できる．

\begin{aligned}
    \int^{t_y}_{t_x} f(t) e^{-i\omega t}{\rm d}t
    &=
    \left\{f(t_x)-t_x\frac{f(t_y)-f(t_x)}{t_y-t_x} \right\}\frac{i}{\omega}(e^{-i\omega t_y}-e^{-i\omega t_x})
    \\&\quad
    +\frac{f(t_y)-f(t_x)}{t_y-t_x}\left\{
    i\frac{t_y e^{-i \omega t_y}-t_x e^{-i \omega t_x}}{\omega}+\frac{e^{-i \omega t_y}-e^{-i \omega t_x}}{\omega^2}\right\}
\end{aligned}

ここで次の積分を用いた．

\int^{t_y}_{t_x} e^{-i\omega t}{\rm d}t=\frac{i}{\omega}(e^{-i\omega t_y}-e^{-i\omega t_x})

\begin{aligned}
    \int^{t_y}_{t_x} t e^{-i\omega t}{\rm d}t
    &=\left[t\frac{i}{\omega}e^{-i\omega t}\right]^{t_y}_{t_x}-\int^{t_y}_{t_x}\frac{i}{\omega}e^{-i\omega t}{\rm d}t\\
    &=i\frac{t_y e^{-i \omega t_y}-t_x e^{-i \omega t_x}}{\omega}+\frac{e^{-i \omega t_y}-e^{-i \omega t_x}}{\omega^2}
\end{aligned}

$1/\omega$に比例する項をまとめると次式のようになる．

\begin{aligned}
    &\int^{t_y}_{t_x} f(t) e^{-i\omega t}{\rm d}t\\
    &=\frac{i}{\omega}\left(-f(t_x)e^{-i\omega t_x}+f(t_y)e^{-i\omega t_y}\right)
    +\frac{1}{\omega^2(t_y-t_x)}(f(t_y)-f(t_x))(e^{-i\omega t_y}-e^{-i\omega t_x})
\end{aligned}

対称性に注意しつつ計算すると，複素定数$C$とその共役$\overline{C}$を用いて，

\begin{aligned}
    \int^{t_y}_{t_x} f(t) e^{-i\omega t}{\rm d}t
    &=f(t_x)e^{-i\omega t_x}C + f(t_y)e^{-i\omega t_y}\overline{C}\\
    &\quad where,\quad C=\frac{1-i\omega(t_y-t_x)-e^{-i\omega(t_y-t_x)}}{\omega^2(t_y-t_x)}     
\end{aligned}

とまとめることができる．

終わりに

これ書いておいてなんだけど，等間隔にサンプルできない時ってあまり無い気がする．
経験ある方教えてください．