本日は確率統計について
目次
[ベルヌーイ分布](## ベルヌーイ分布)
[二項分布](## 二項分布)
ガウス分布(正規分布)
[最尤推定](# 最尤推定)
ベルヌーイ分布
ベルヌーイ分布とは2値を取る変数(例;コイントス)が生成する確率分布を示します。
$f(k)=p^k(1-p)^{1-k}$
$p$は確率、$k$はパラメータを示します。
例えばコイントスの表が出る確率はベルヌーイ分布に従います($p=0.5$, $k=0:$裏, $k=1:$表 )。
$k$の値は1の時が成功、0が失敗と割り当てられています。
二項分布
ベルヌーイ試行を$n$回行い、$x$回成功する回数が従う確率分布を示します。
$B(n,p)=_nC_xp^x(1-p)^{n-x}$
$n$は試行回数、$p$は成功確率を示します。
コイントスで言うなら$n$回投げて表が$x$回出る回数($=x$回成功する)が従う確率分布とお考え下さい。
マルチヌーイ分布
マルチヌーイ分布(カテゴリカル分布)とはベルヌーイ分布をn次元に拡張した確率分布です。
名前の通りベルヌーイの複数版(マルチ)とお考え下さい。
$f(x_i)=\frac{n!}{x_1! … x_k!}p_1^{x_1}…p_k^{x_k}$
$ (p_{1} + p_{2} + ... + p_{k} = 1)$
$x_j$は試行回数、$p_j$はラベルjの事象の確率です。
例えばサイコロの確率が従います。
$n$回投げて$p_i$の確率で出現する面$i$が$x$回出る回数が従う分布と考えられます。
サイコロなら$i$はラベル($i=1$:なら$1$の目)、確率$p_i$は
$ p_{1} = p_{2} = ... = p_{6} = \frac{1}{6}$
です。
ガウス分布(正規分布)
あの磁石で有名なガウスさんが考え付いた確率分布です。
エンジンの駆動データ、インターネットのアクセスに関するデータなど様々なデータがこの分布に従うことが知られています。
$N(\mu,\sigma^2)=\frac{1}{\sqrt{2\pi \sigma ^2}} \exp \left( -\frac{(x-\mu)^2}{2\sigma ^2} \right)$
期待値$E(x)=\mu$
分散$V(x)=\sigma ^2$
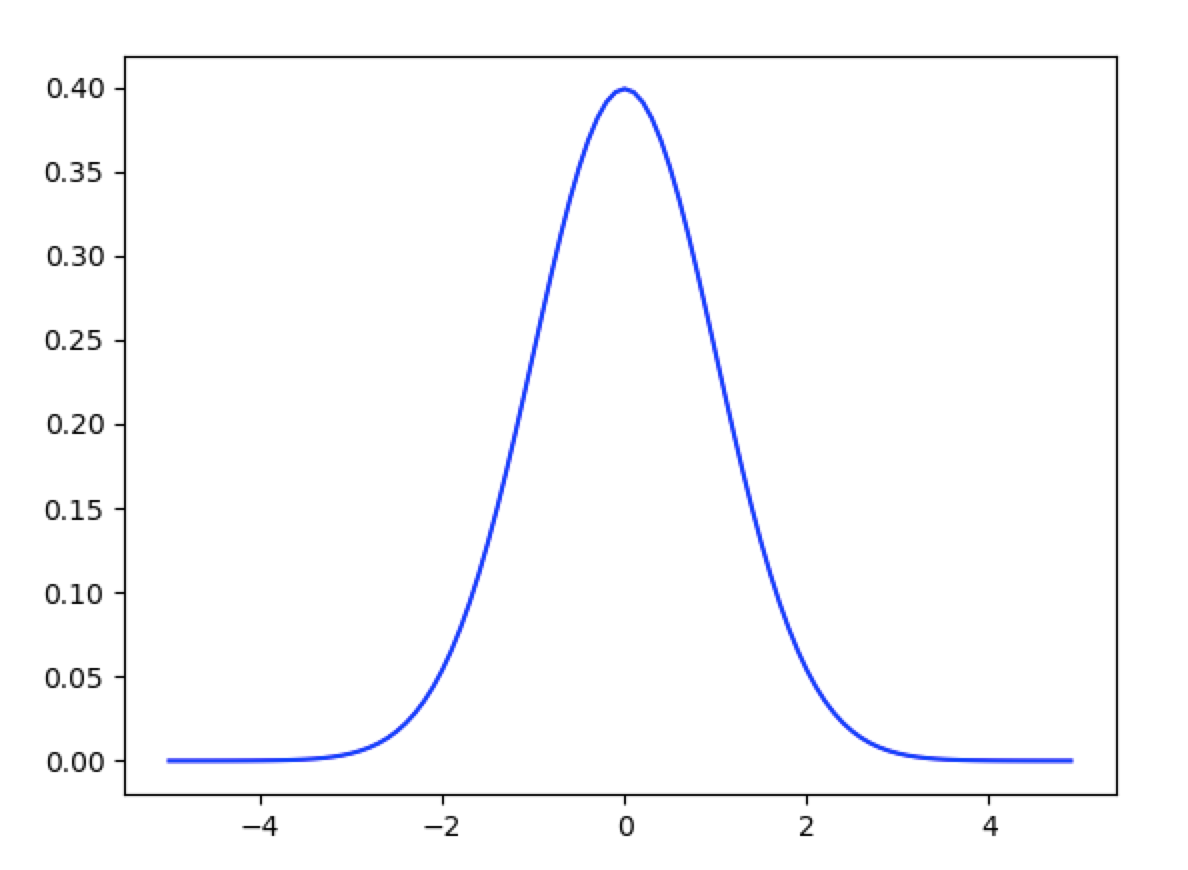
引用:https://www.python.ambitious-engineer.com/archives/2174
グラフにするとこう。
また$N=0,\sigma^2=1$のとき、標準正規分布と呼ばれます。
最尤推定
(シラバスには書いてなかったものの、どうやら出題されるみたいなので書きます。)
最尤推定とは尤度関数$L(\theta)$を最大にする$\theta$を求めることをさします。
とりあえず例題を見て確認しましょう。
例題
さいころを10回投げた時、1の目が3回出た。1の目が出る確率を最尤推定せよ。
例題は二項定理の確率分布に従います。
解く問題は「$B(10,p)$を最大化する$p$を求める」です。例題は
$B(10,p)=_{10}C_3p^3(1-p)^{10-3}$
と書けます。
$B(10,p)=L(\theta)~~(p=\theta)$
とおき、微分します。
このまま微分してもいいのですが、対数をとってから微分すると計算が楽になります。
まず対数をとると
logL(\theta)=log(_{10}C_3\theta^3(1-\theta)^{7})
=log(_{10}C_3)+log\theta^3+log(1-\theta)^{7}
次に微分し、極値を求めます。
\begin{eqnarray}
\frac{d~logL(\theta)}{d\theta} = \frac{3}{\theta} - \frac{7}{1-\theta} \\
\frac{dL(\theta)}{d\theta} =L(\theta)( \frac{3}{\theta} - \frac{7}{1-\theta})=0 \\
10\theta=3
\end{eqnarray}
よって求める確率$\theta$は
$\theta=0.3$
です。
以上になります。
参考文献
https://to-kei.net/distribution/bernoulli-distribution/