今日は活性化関数について。
目次
活性化関数とは
万能近似定理
作図に用いたコード
参考文献
活性化関数とは
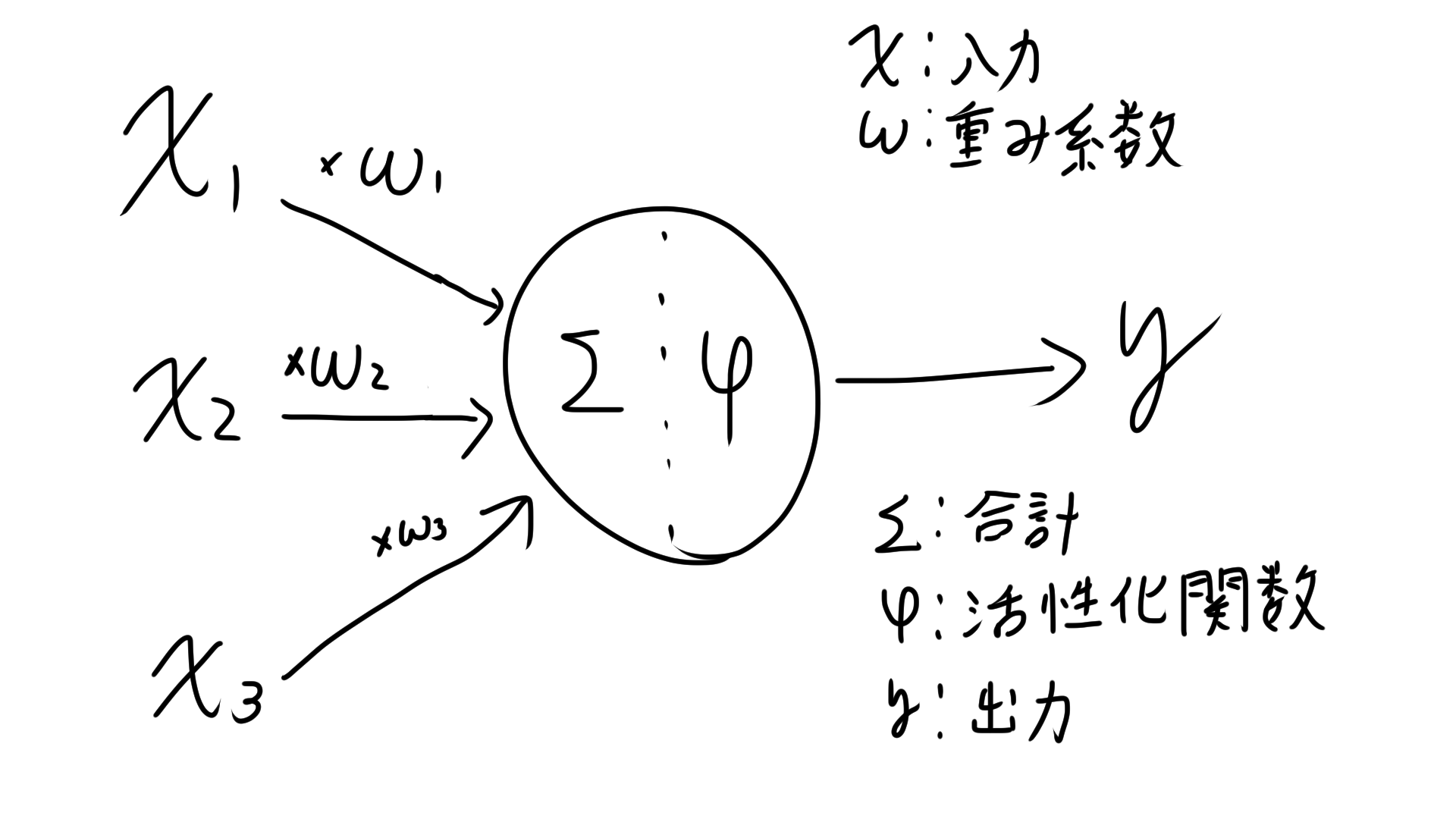
上図のφに当たる部分になります。活性化関数を通すと出力結果が非線形になるため学習に寄与します。
ニューロンでは入力を受け取り、何かしらの処理をしてから出力をします。
その処理を行う関数が活性化関数です。
求められている性質は
・微分可能
・非線形性
の2つです。また
・隠れユニット
・出力ユニット
の2種類があります。
出力ユニット
出力ユニットでは人間が欲しい結果の形式に合わせて何を使うか選びます。
線形ユニット
入力をx、重み係数をw、出力をyとすれば
$$
y=w^Tx
$$
です。
NNの結果が欲しい時、例えば株価の予想などに使用します。
シグモイドユニット
$$
y=\frac{1}{1+exp(-w^Tx)} \
=\sigma (w^Tx)
$$
と書きます。
グラフに書くとこう。式が簡単、連続で有界(微分可能)、yは0~1で二値分類などで扱えるので多く使われます。
ソフトマックスユニット
$$
y_k=\frac{exp(x_k)}{\sum_{j=1}^{N}exp(x_j)} \
$$
と書きます。シグモイドの多クラス版とお考え下さい。
また
$y_1+y_2+\cdots + y_N=1$
を満たすので確率(例えば晴れの確率0.4,雨の確率0.3,曇りの確率0.3だから明日は晴れ)として扱えます。
隠れユニット
隠れユニットでは計算速度向上が求められています。
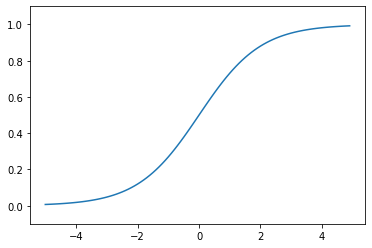
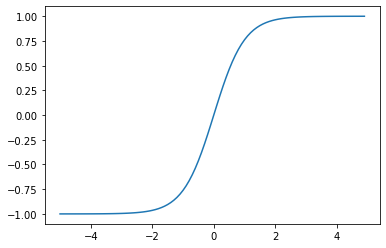
sigmoid
先ほど出てきたシグモイドです。
グラフに書くとこう。
微分についてですが
$f(x)=\sigma (w^Tx)$
とすると
$$
f(x)'=(1-f(x))f(x)
$$
が成り立ち、簡単な式で表せます。のちに出てくる誤差伝播法で使いますので覚えてください。
ただこの関数には
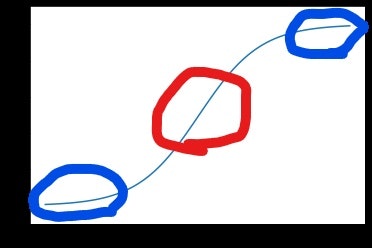
・入力が大きいと勾配が消える(赤丸)
・入力0付近に敏感、線形ニューロンになる(青〇)
の欠点があります。
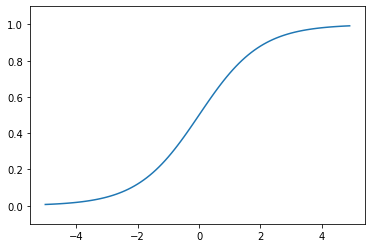
Tanh
ハイパボリックタンジェントと読みます。式は
$$
f(w^Tx)=\frac{e^{w^Tx}-e^{-w^Tx}}{e^{w^Tx}+e^{-w^Tx}}
$$
です。
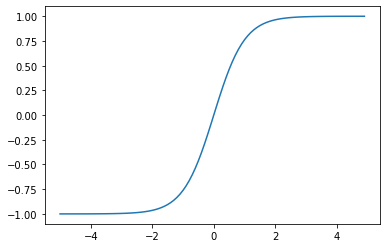
グラフはこう。sigmoidと似ていますがsigmoidは0~1の値をとるのに対し、tanhは-1~1の値をとります。
微分についてですが
$$
f(x)'=1-f(x)^2
$$
が成り立ちます。のちに出てくる誤差伝播法で使いますので覚えてください。
ただこの関数もシグモイドと同様に
・入力が大きいと勾配が消える
・入力0付近に敏感、線形ニューロンになる
の欠点があります。
ちなみに
$$
tanh(z)=2\sigma(z)-1
$$
です。
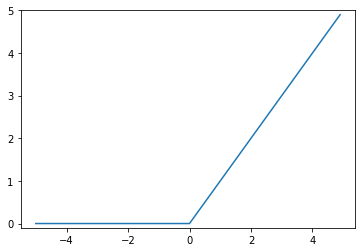
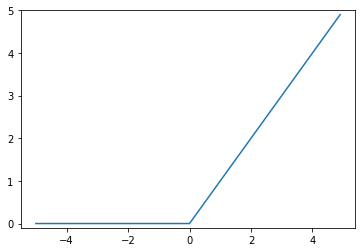
ReLU:Rectified Linear Unit
正規化線形関数とも呼ばれます。
式は
$$
f(x)=max(0,x)
$$
と書きます。
グラフはこう。
メリットは以下の通り
・勾配が消えない
・計算コストが低い
・性能が良い
・非線形性が強い
といいことずくし。
微分はできないので劣微分をすると
f(x) '= \left\{
\begin{array}{ll}
1 & (x \geq 0) \\
0 & (x \lt 0)
\end{array}
\right.
と表現できます。
万能近似定理
知識として万能近似定理は知ってください。
定数でない有界で非線形な隠れユニットを使用すればどんな問題でも表現可能という定理。
表現可能ってのがポイントで、学習可能かは保障していません。
またネットワークは深く狭く作れば
・表現能力を保つ
・パラメータを減らす
ことができると提案しています。
作図に用いたコード
sigmoid
import numpy as np
import matplotlib.pylab as plt
def sigmoid(x):
return 1/(1+np.exp(-x))
x=np.arange(-5,5,0.1)
y=sigmoid(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show
tanh
import numpy as np
import matplotlib.pylab as plt
x=np.arange(-5,5,0.1)
y=np.tanh(x) #tanhはnumpyの中に入っています
plt.plot(x,y)
plt.ylim(-1.1,1.1)
plt.show
RelU
import numpy as np
import matplotlib.pylab as plt
def relu(x):
return np.maximum(0,x)
x=np.arange(-5,5,0.1)
y=np.tanh(x)
plt.plot(x,y)
plt.ylim(-1.1,1.1)
plt.show
参考文献
ゼロから作るDeep Learning: Pythonで学ぶディープラーニングの理論と実装