では書きます。
教師あり学習とは
原因と結果のペアのデータから規則を学び、新しいデータに対して予測を行う手法です。以下の2つがあります。
分類
複数クラスに分類したいとき
例:退職予測(原因には欠勤日数、給与、役職などさまざまなものが考えられます。)
回帰
連続値を予測したいとき
例:株価予測(原因には倒産件数、エンゲル係数などさまざまなものが考えられます。)
今回は分類手法についてまとめました
最近傍法
予測したいデータが入ってきたとき、そのデータに最も距離が近いデータのラベルを予測値とする手法です。
コードはこちら
import mglearn
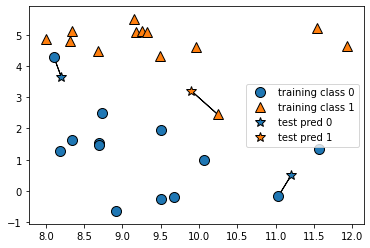
mglearn.plots.plot_knn_classification(n_neighbors=1)
上図が実際に最近傍法で分類している様子、☆がテスト値で一番近い値のラベルを予測値として出しています。
ただメモリに学習データをすべて保存しないといけないのでメモリを消費します。
k近傍法
最近傍法の複数版、予測を多数決で行います。
kは多数決をとる数、つまり距離が近いk個のデータで多い方のラベルを予測値とします。
import mglearn
mglearn.plots.plot_knn_classification(n_neighbors=3)#n_neighbors=1が最近傍法
kの値を増やすと・・・?
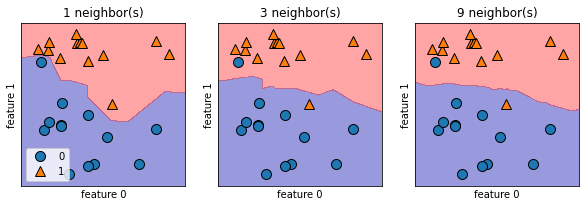
kを増やすと境界線はどうなるのでしょうか。
上図は左から順にk=1(=最近傍法),k=3,k=9の時の境界線を示しています。kが増えるにつれて境界線が滑らかになります。
コードはこちら
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1,3, figsize=(10,3))
for n_neighbors, ax in zip([1,3,9],axes):
clf= KNeighborsClassifier(n_neighbors=n_neighbors).fit(X,y)
mglearn.plots.plot_2d_separator(clf,X,fill=True,eps=0.5,ax=ax,alpha=.4)
mglearn.discrete_scatter(X[:,0],X[:,1],y,ax=ax)
ax.set_title("{} neighbor(s)".format(n_neighbors))
ax.set_xlabel("feature 0")
ax.set_ylabel("feature 1")
axes[0].legend(loc=3)
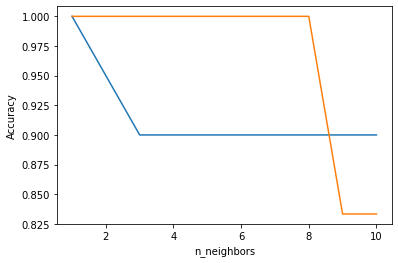
では正答率はkを増やすと上がるのでしょうか。
やみくもにkを増やすと過学習が起きてしまうようです。
コードはこちら。
training_accuracy=[]
test_accuracy=[]
neighbors_settings = range(1,11)
for n_neighbors in neighbors_settings:
#create model
clf = KNeighborsClassifier(n_neighbors=n_neighbors)
clf.fit(X_train,y_train)
#record train
training_accuracy.append(clf.score(X_train,y_train))
#record test accuracy
test_accuracy.append(clf.score(X_test,y_test))
plt.plot(neighbors_settings, training_accuracy, label="training accuracy")
plt.plot(neighbors_settings, test_accuracy, label="test accuracy")
plt.ylabel("Accuracy")
plt.xlabel("n_neighbors")
plt.legend
線形分離モデル
k近傍法では学習データを全てとっておく必要があるため、メモリを消費してしまいました。
なので判別面を決めて「これより上は1,これより下は-1」とプロットされたデータを分類しましょうというのが線形分離モデルです。
ロジスティック回帰
超ざっくりいえば
$$
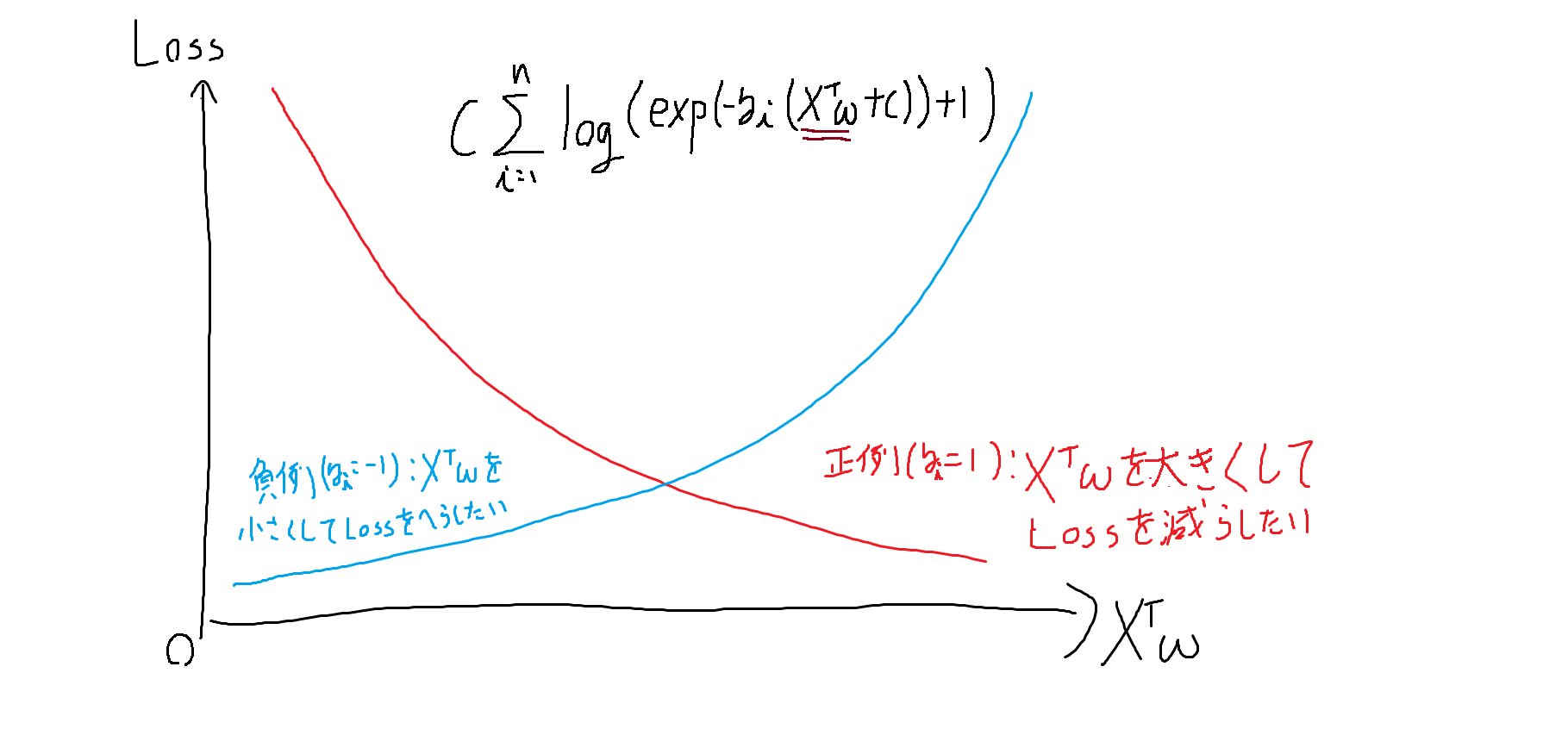
\frac{1}{2}w^Tw+C\sum_{i=1}^n log(exp(-y_i(X^Tw+c))+1)
$$
$\frac{1}{2}w^Tw$はL2正則化項、Cはハイパーパラメータです。
の$w$と$C$についての最小化問題を解いて$w$を学習させる手法です。
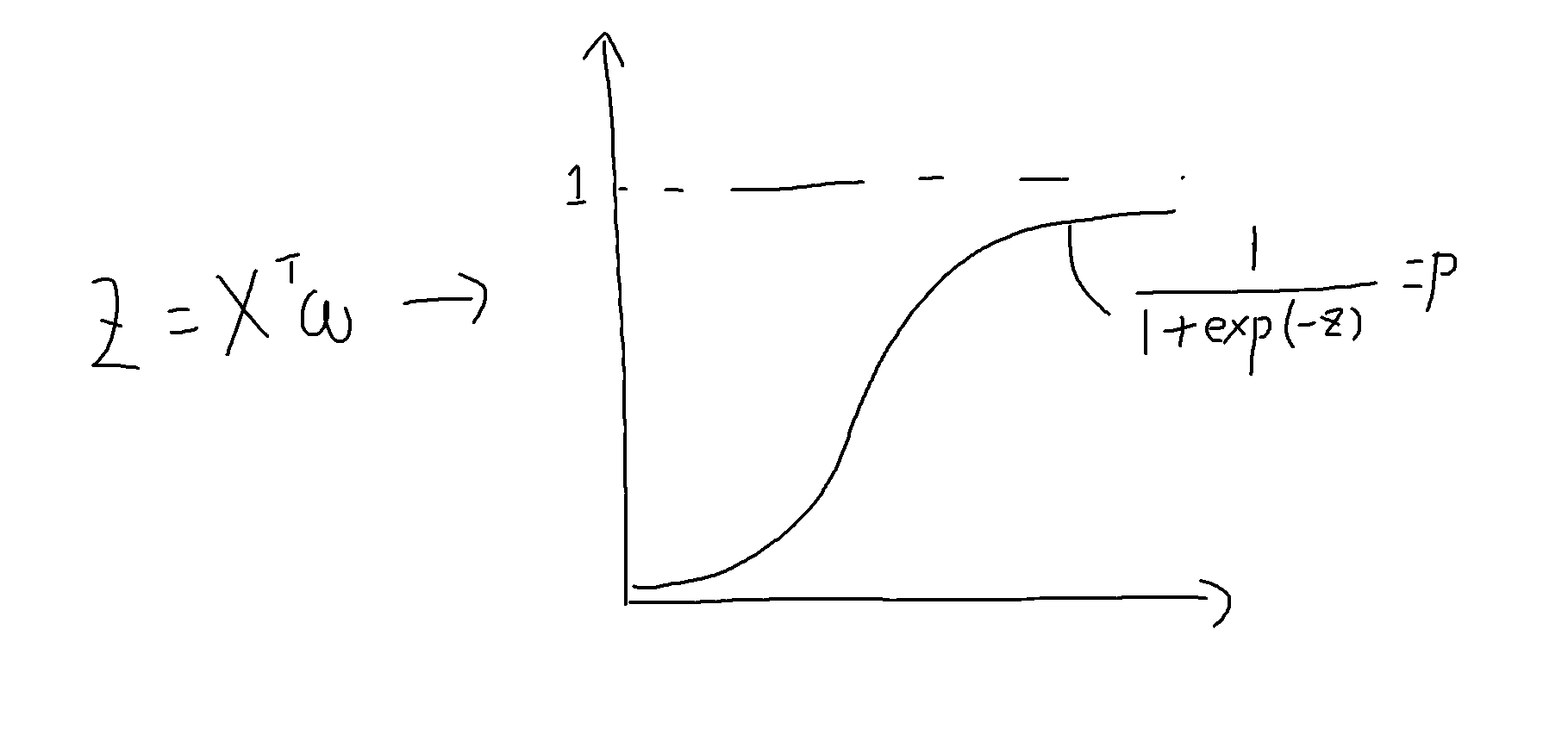
上図のように正例が与えられたときは$X^Tw$を大きく、負例が与えられたときは$X^Tw$を小さくするよう$w$を学習します。
学習し終わったら、$X^Tw$をロジスティック関数(シグモイド関数)に入れて、正例である確率、負例である確率を比較し、分類します。
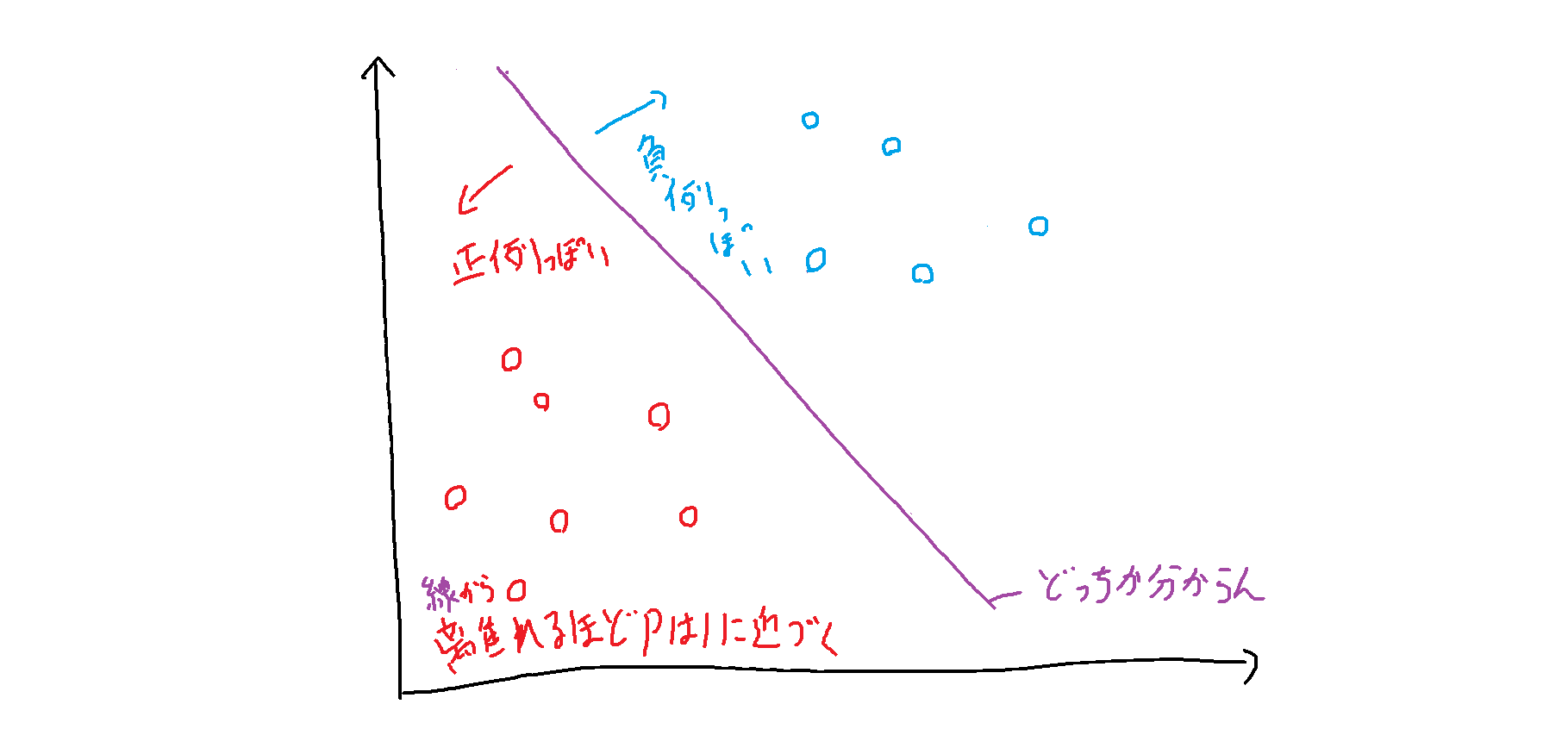
正例か負例かどっちかわからないところに境界線を引くと直線になるので線形分類のカテゴリに位置付けられています。
境界線から離れるほど1に確率は近づきます(尤もらしくなる)。
SVM
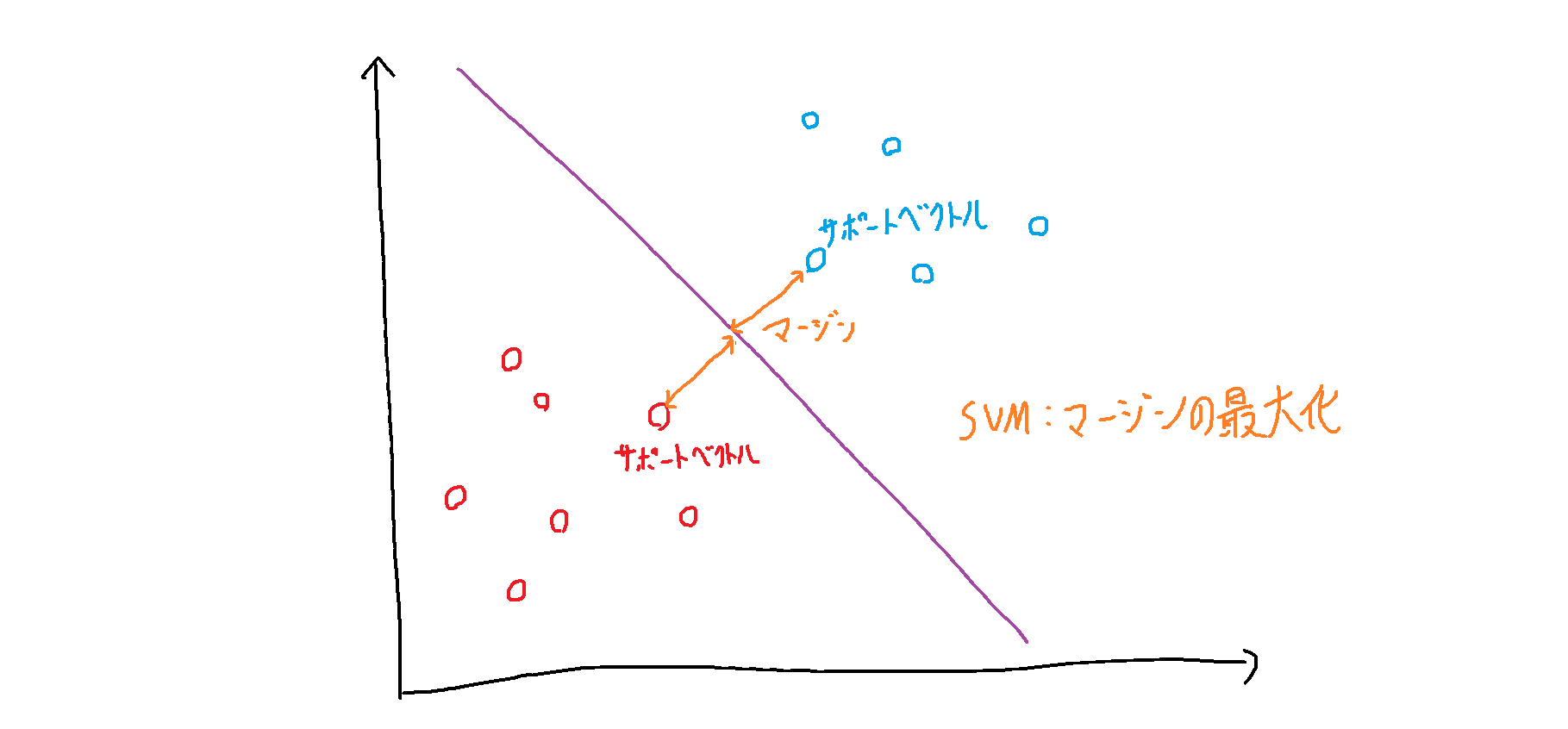
各データ点からの距離(マージン)が最大になるところに境界線を引く手法です。
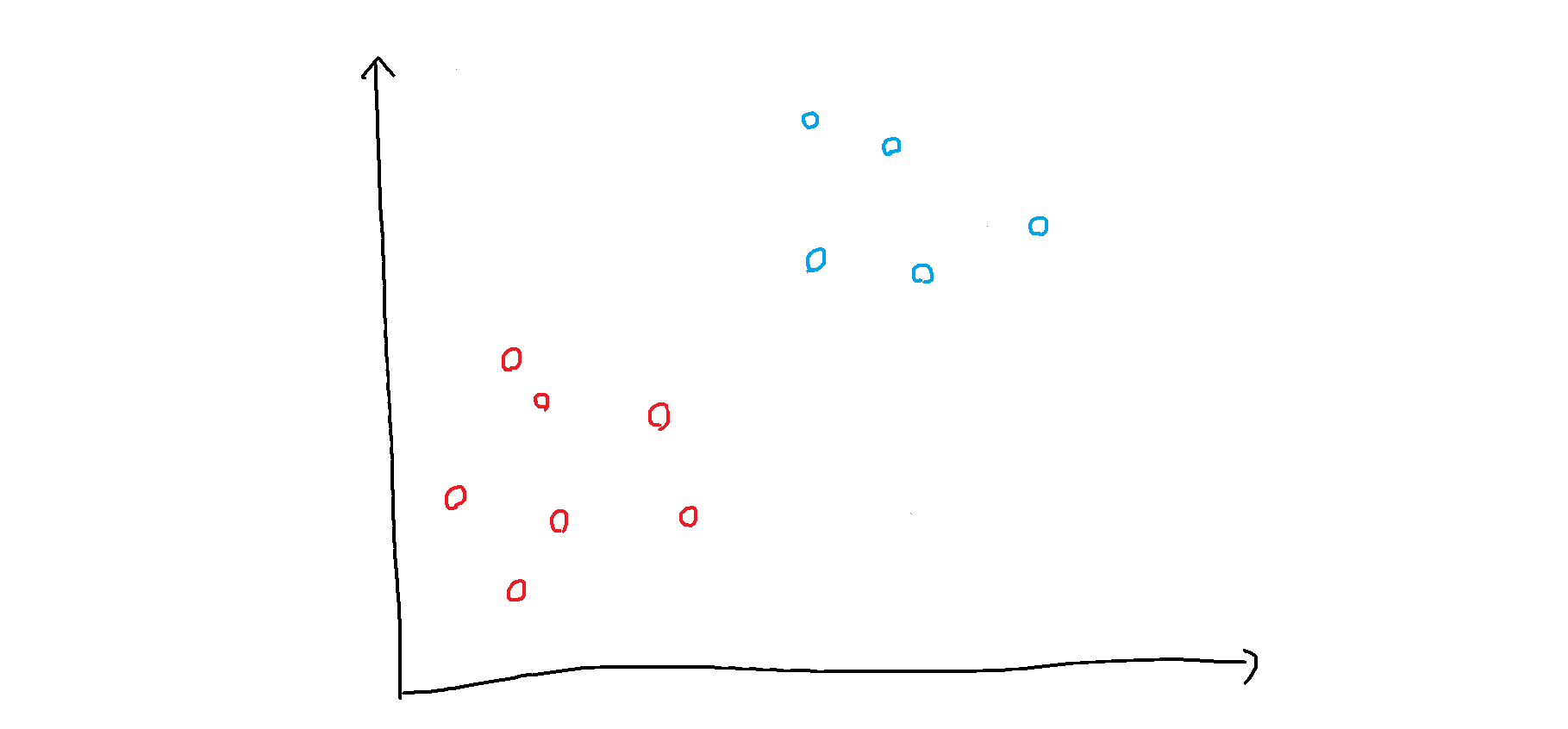
例えば下図のようなデータの分布があったとします。
ここにsvmで境界線を作るならこんな感じ
境界線に一番近いデータ点をサポートベクトルと言います。
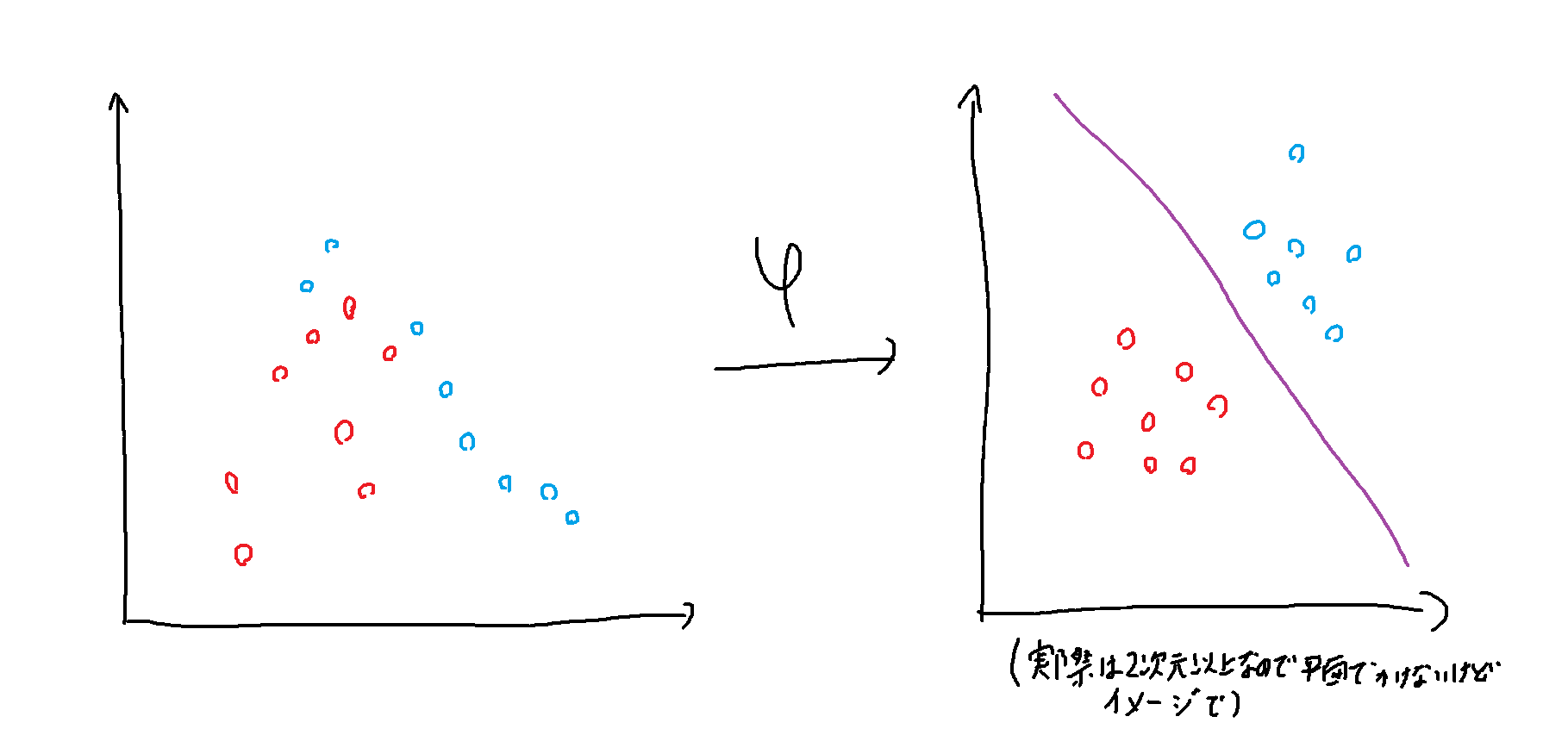
カーネルトリック
いい感じで直線に分類できればいいのですが、データの分布上できないものも多いです。
そこでSVMはデータを高次元(例えば2次元から6次元)に関数で変換し、変換先で境界線を引けます。
この高次元上ではパラメータが増えるので普通計算量が増えます。
ですが計算量がSVMでは高次元の計算をもとの次元数の計算でできちゃいます。
この中間層(6次元)の内積計算が入力層(2次元)の内積で計算できることをカーネルトリックといいます。
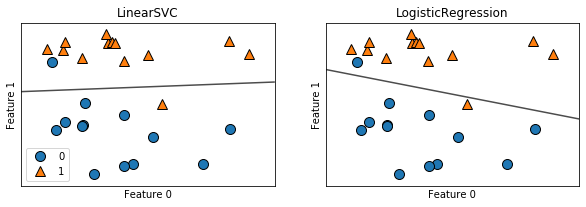
手法の比較
実際に動かしてみましょう。
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
X,y = mglearn.datasets.make_forge()
fig, axes = plt.subplots(1,2,figsize=(10,3))
for model, ax in zip ([LinearSVC(),LogisticRegression()],axes):
clf=model.fit(X,y)
mglearn.plots.plot_2d_separator(clf,X,fill=False,eps=0.5,ax=ax, alpha=.7)
mglearn.discrete_scatter(X[:,0],X[:,1],y,ax=ax)
ax.set_title("{}".format(clf.__class__.__name__))
ax.set_xlabel("Feature 0")
ax.set_ylabel("Feature 1")
axes[0].legend()
参考文献
Pythonではじめる機械学習 ―scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎