はじめに
この記事では、書籍「実践XAI[説明可能なAI] 機械学習の予測を説明するためのPythonコーディング」を参考にして、PDPで機械学習モデルを解釈する方法を解説します。
また、記事の最後には付録として、書籍「実践XAI」の補足説明を掲載しています(非公式)。
※書籍は「初版第1刷」を参考にしています。第2刷以降ではページ数・内容に変更がある場合がありますので予めご了承ください。
部分従属プロット(PDP)
書籍対応箇所:p.42~43
概要
部分従属プロット(Partial Dependency Plot; PDP)では、他の変数を固定したまま、ある変数を動かしたときにモデル$f(\cdot)$の出力がどう変化するかを見ることができます。
部分従属プロット(以下、PDPと略す)は下図のようなものです(shap.plots.partial_dependenceで描画)。
横軸は特徴量Ageの値を表し、縦軸は特徴量Age以外の変数を固定したときのモデル$f(\cdot)$の出力の期待値を表します。
下部にある棒グラフはAgeの分布を表します。
この説明では少し分かりづらいかもしれないので、もう少しかみ砕いて説明しましょう。
中古車価格Priceを、2つの説明変数
- 走行距離:Odometer($x_1$)
- 使用年数:Age($x_2$)
を用いて、線形モデル$f(x_1. x_2)=\beta_0 + \beta_1x_1 + \beta_2x_2$で予測することを考えます。
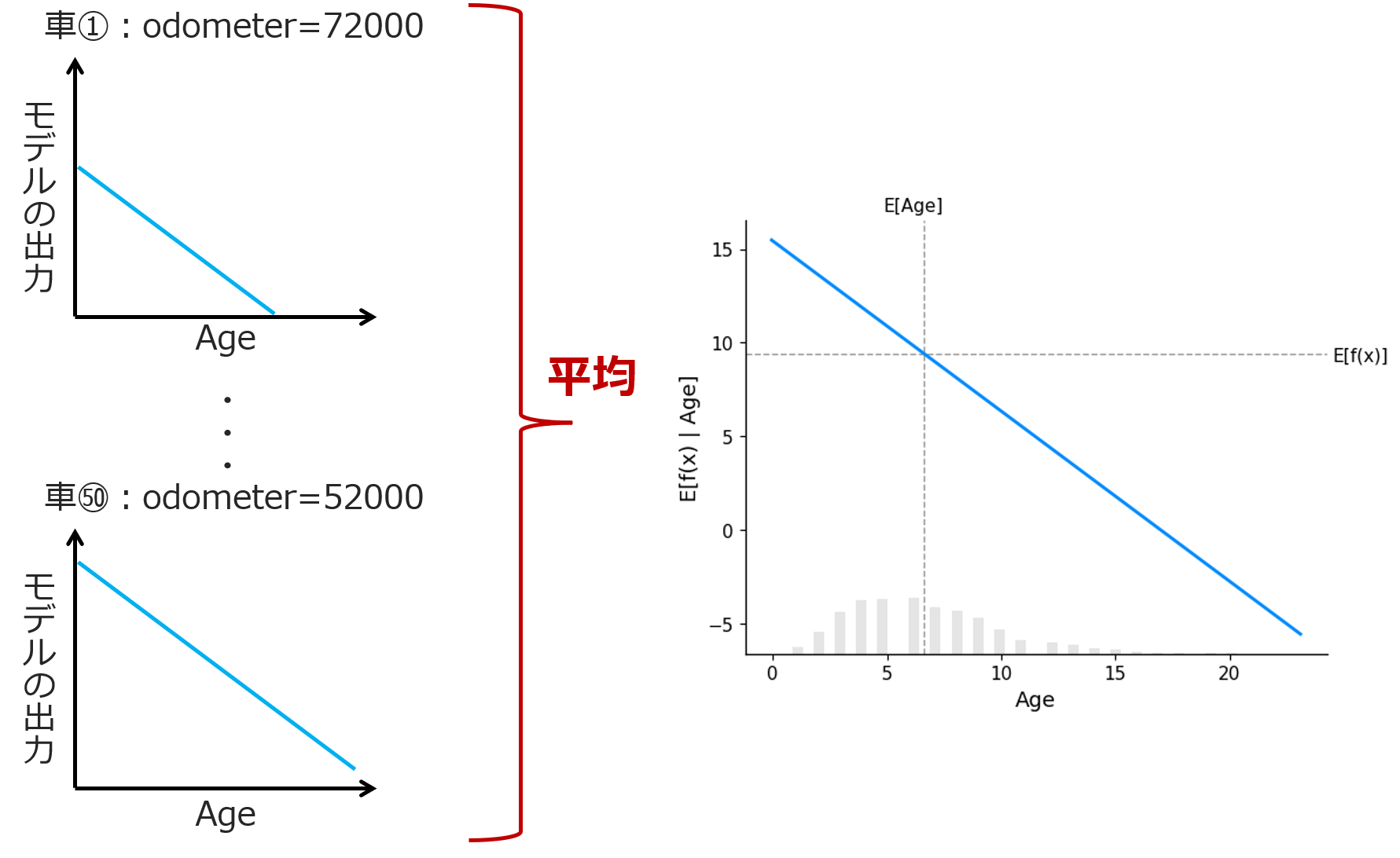
例えば車①でOdometer=72000だとしましょう。この値($x_1=72000$)を線形モデルの式に代入すると
$f(x_1=72000, x_2) = \beta_0 + 72000\beta_1 + \beta_2x_2$
となり、傾きが$\beta_2$・y切片が$\beta_0 + 72000\beta_1$の直線となります。これをプロットすると下図左上のグラフのようになりますね。
同様に他の車についてもプロットしていきます。
これらをすべて足し合わせて平均すると、平均(≒期待値)が求まります。これが先ほどのPDPとなるわけです。
見方
以上を踏まえれば、PDPの見方は分かると思いますが、念のため確認しておきましょう。
下図は、特徴量Odometerに対するPDPです。
モデルはRandomForest(非線型なモデル)を使用したため、PDPは直線ではないことに注意してください。
図によると、Odometerがある値を超えると価格が一気に(3単位ほど)減少することがわかります。
このようにPDPを見れば、特徴量重要度や回帰係数などでは確認できなかった、特徴量と目的変数との定量的な関係性を確認することができます。
付録
ここでは、書籍「実践XAI」における説明やコードの不備、および私からのツッコミを付録として載せておきます。ここでの対象範囲は43ページのPDPの説明まで。それ以降はまた次回の記事で。
実はこれら以外にもツッコミどころ(文章構成がおかしい、図が意味をなしていない、など)があるのですが、挙げていくとキリがないほど多いので割愛しました。
A:【コード不備】説明変数に目的変数が入っている
- 該当箇所:p.34
- 不備内容:説明変数に目的変数が入ってしまっている実装ミス。これに伴う説明にも不備あり。
- 2023/8/16現在、正誤表に記載なし
- 出版社に問い合わせ済み
以下は書籍(初版第1刷)のコードからの引用です。
# データセットを訓練データセットとテストデータセットに分割
data_train, data_test = train_test_split(clean_df,test_size=0.25,random_state=1234)
data_train.shape,data_test.shape
XTrain = np.array(data_train.iloc[:,0:(clean_df.shape[1]-1)])
YTrain = np.array(data_train['Price'])
XTest = np.array(data_test.iloc[:,0:(clean_df.shape[1]-1)])
YTest = np.array(data_test['Price'])
XTrain.shape, XTest.shape
# ((4514, 23), (1505, 23))
ここで、clean_dfの中身を見てみます。(これも書籍p.33~34に記載あり)
Index(['Price', 'Age', 'Odometer', 'mileage', 'engineCC', 'powerBhp',
'Location_Bangalore', 'Location_Chennai', 'Location_Coimbatore',
'Location_Delhi', 'Location_Hyderabad', 'Location_Jaipur',
'Location_Kochi', 'Location_Kolkata', 'Location_Mumbai',
'Location_Pune', 'FuelType_Diesel', 'FuelType_Electric', 'FuelType_LPG',
'FuelType_Petrol', 'Transmission_Manual',
'OwnerType_Fourth +ACY- Above', 'OwnerType_Second', 'OwnerType_Third'],
dtype='object')
これを踏まえると、上記コードのこの部分:
XTrain = np.array(data_train.iloc[:,0:(clean_df.shape[1]-1)])
は、目的変数PriceをXTrainに含めていることになっています。
それゆえ、データリークが生じて「決定係数が1.0」という状況に陥ってしまいます。
このおかしな状況は筆者も気づいているようで、p.34~35では次のように述べています。
係数を調べてみると、すべての係数が0で、切片項が0.0、決定係数が1.0であることがわかる。何かが間違っている。
[中略]
回帰分析の結果の概要は、モデルの作成プロセスに問題があることを示している。原因として考えられるのは、強い多重共線性である。
多重共線性が原因であると言っており、まったくの見当違いをしています。しかも「すべての係数が0」というのはウソで、変数Priceに対する回帰係数は「1」になるはずです。
決定係数が1.0になったらまず疑うべきことは、データリークでは…?
B:【ツッコミ】相関係数
- 該当箇所:p.32~33
不備ではないが、ツッコミどころがあったので紹介しておきます。
場合によっては、相関係数の表に見せかけの相関が表示されることもある。相関が見せかけかどうかを検証するには、数値特徴量と目的変数の間の相関係数ごとに統計学的有意性を用いる必要がある。
np.where((df[['Price','Age','Odometer','mileage','engineCC','powerBhp']]).corr()>0.6,'Yes','No')
- ツッコミ1:「統計学的有意性を用いる必要がある」と言っておきながら統計学的有意性を用いていない。
- ツッコミ2:この直前部分で相関係数を全部見れるコードを書いたので、わざわざこのコードで'Yes'とか'No'とか出す必要があない
- ツッコミ3:
.corr()>0.6とあるが、負の強い相関は無視?絶対値取って>0.6とするべき。
ここで言っている統計学的有意性というのは、無相関の検定、すなわち
- 帰無仮説$H_0$:説明変数$X$と目的変数$Y$の相関係数($=r_{XY}$)は0
- 対立仮説$H_1$:$r_{XY}\ne0$
において有意性がみられるかどうか、ということを言っているのでしょう。検定統計量は
$$t=\frac{|r|\sqrt{n-2}}{\sqrt{1-r^2}}$$
です。ここで$r$は標本相関係数、$n$はサンプルサイズです。
帰無仮説$H_0$のもとで$t$はt分布に従うことが知られているので、これを用いて検定を行えばよいです[1]。
C:線形モデルにおける特徴量重要度の指標
- 該当箇所:p.42
入力パラメータを変更したときに目的変数がどのように予測(推定)されるのかをモデルの係数から理解できる。ただし、どの特徴量が重要であるかまでは教えてくれない。各係数の値は入力特徴量の尺度に依存する。たとえば、車の使用年数は0~15年の間であると考えることができる。これに対し、上記のデータセットでは、馬力の範囲は34.20~560.00bhpである。したがって、線形モデルでは、モデルの係数の大きさが特徴量の重要度のよい目安になるとは限らない。
確かに、説明変数のスケール(尺度)が揃っていない場合、回帰係数の大きさは特徴量重要度とみなせません。ですが、説明変数を正規化または標準化するなどしてスケールをそろえることで、回帰係数は特徴量重要度として捉えることが可能です。
次回予告
次回は「SHAPによるモデルの説明」というテーマで解説します。
参考記事
[1] 統計Web「26-3. 相関係数」
https://bellcurve.jp/statistics/course/9591.html