Go to Qiita Advent Calendar 2024 Top
LoginSignup
4
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

データ構造とアルゴリズムAdvent Calendar 2021

Day 18
@MatsuTaku(Takuma Matsumoto)

Quotient Filterとコンパクトなハッシュテーブル

Last updated at Posted at 2021-12-17

この記事はデータ構造とアルゴリズム Advent Calendar 2021 18日目の記事です．

はじめに

Approximate Membership Query (AMQ)とは，データ集合に任意の要素があるかどうかを判定する確率的クエリです．
AMQは偽陽性(検索にヒットしたが，実際にデータは存在しない)を一定の確率で含むという曖昧性を許すことで，偽陽性率とのトレードオフとして省メモリ化を実現します．
AMQは例えば以下のようなシーンで用いられます．

  • 巨大DBで検索をする前に，データがDBにあるかどうかをin-memoryなAMQで確認しておことで，DBへの高負荷な検索回数を軽減する．
  • ビットコインにおいて，あるノードに関連するトランザクションを取得するシーンがある．全てのトランザクションをダウンロードしてからノードの関連性を調べていては非効率なので，AMQでノードを絞り込んでからトランザクションのダウンロードを行う．

代表的なAMQデータ構造としてBloom Filter, Quotient Filter, Cuckoo Filterがあります．
本記事ではAMQの一つであるQuotient　Filterの解説と，Quotient Filterを用いたコンパクトなハッシュテーブルの実現方法を解説します．
Quotient Filterは，ハッシュテーブルの実装技法の一つであるオープンアドレス法に近いため，教科書などのオープンアドレス法の解説と併せて読むと理解しやすいかもしれません．

関連記事

準備

$p$bitのハッシュ値を生成する関数$\mathrm{hash}$を定義する．
任意の型で表現される値$x$に対するハッシュ値を$\mathrm{hash}(x)$とする．
$q\ (q \le p)$をパラメータとして，ハッシュ値の上位$q$bitをquotient(商), 下位$r=(p-q)$bitをremainder(あまり)と呼ぶ．

Quotient Filter

Quotient Filter1は，オープンアドレス法に近い考え方で設計されたAMQである．
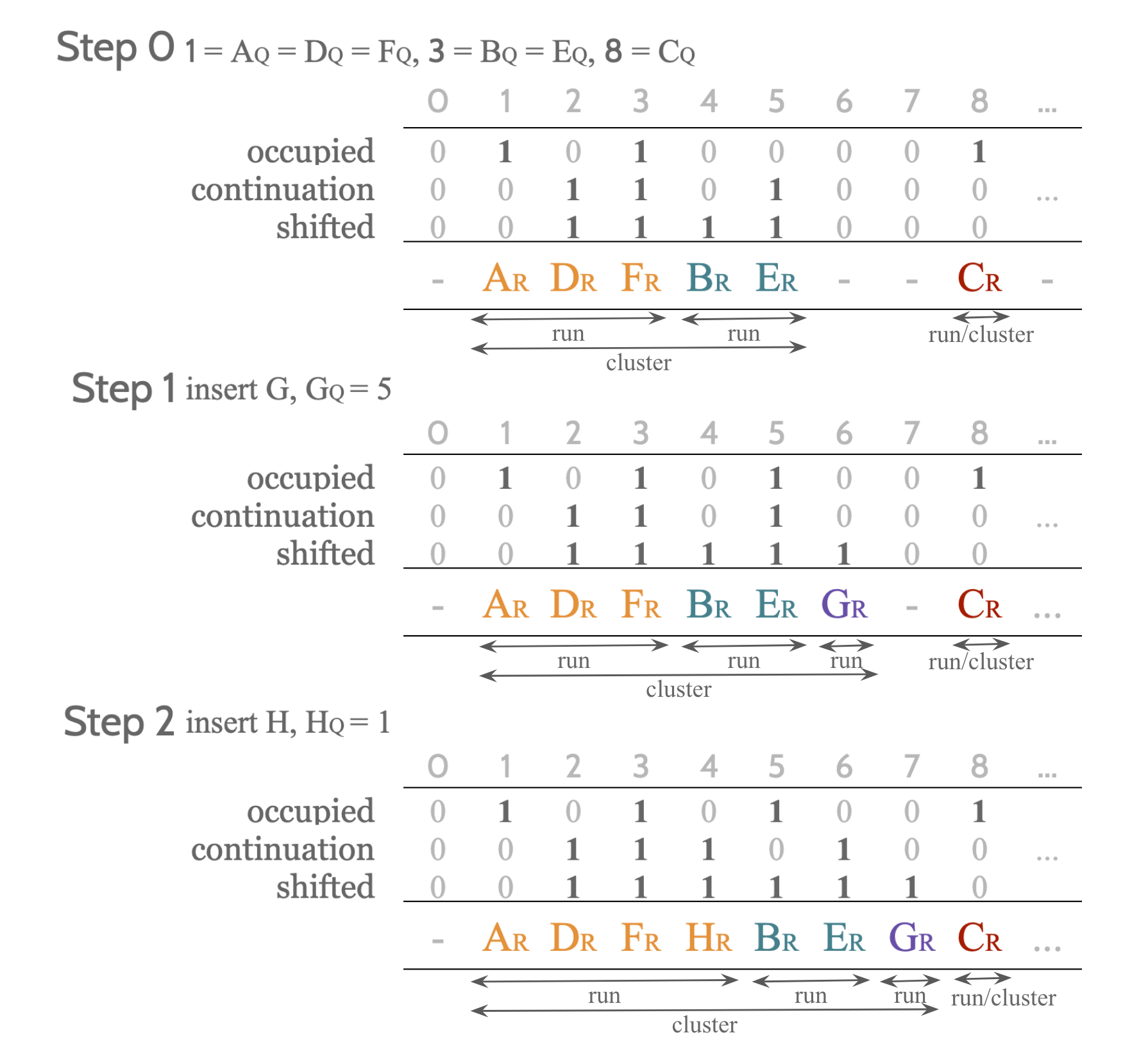
データを追加する際，データから$p$bitのランダムなフィンガープリントを生成し，フィンガープリントの上位$q$bitのquotientをインデックスの基準として配列上に保存していくというものである．
一般的なハッシュテーブル向けのオープンアドレス法との違いとして，同じquotientを持つ要素は必ず隣接するように配置する．
配列上で隣接する同じメタデータの塊をrunと呼び，隣接したrunの塊をclusterと呼ぶ．

用意するデータ構造は，Quotient Filterのバケットサイズを$2^q$として，3つの長さ$2^q$のビット列$\mathrm{occupied}, \mathrm{continuation},\mathrm{shifted}$と，長さ$2^q$の整数配列$\mathrm{R}$である．
$\mathrm{occipied}$は，保存されたある値$x$のquotientが$i$であるときに$\mathrm{occupied}[i]=1$を保存する．
$\mathrm{continuation}$は，インデックス$i$に値が存在し，それがrunの先頭ではないとき$\mathrm{continuation}=1$を保存する．
$\mathrm{shifted}$は，インデックス$i$に保存された値のquotientが$i$と**異なる(シフトされた)**とき$\mathrm{shifted}=1$を保存する．
$\mathrm{R}$には保存された値$x$のremainderをそのまま保存する．

scrnli_2021_12_18 0-33-17.png

検索

$X=\mathrm{hash}(x)$のquotientを$X_Q=\lfloor X/2^r \rfloor$，remainderを$X_R=X \mod 2^r$とする．
まず$X_Q$が既にquotientとして利用されているかどうかを調べる．
$\mathrm{occupieds}[X_Q] = 0$ならば$x$は存在しない．
$\mathrm{occupieds}[X_Q] = 1$ならば，$X_Q$が属するrunを特定し，runの中に$X_R$あるかどうかを探すことになる．
まずclusterの先頭を見つける．
$j=X_Q$とし，$\mathrm{shifted}[j]=0$となるまで$j$を左に移動させる．
その際，$X_Q$の属するrunがclusterの左から何番目のrunであるかを記録する．
これは，$j$を左に移動している時に見つけた$\mathrm{occupieds}[j]=1$の数を数えれば良い．
$X_Q$が属するrunの先頭は，$j$がrunの先頭となる回数$(\mathrm{continuation}[j]=0)$を数えながら$j$を右に移動して見つける．
こうして見つけたrun$=\left[f_{X_Q},b_{X_Q}\right]$の中に$\mathrm{R}[j]=X_R\ (f_{X_Q} \le j \le b_{X_Q})$となる$j$があれば検索成功とする．

m = 1 << q
def left(i):
    j = i-1
    if j < 0: j = m-1
    return j
def right(i):
    j = i+1
    if j == m: j = 0
    return j

def find(x):
    X = hash(x) # 0 <= hash(x) < (1 << p)
    Xq = X >> r
    Xr = X & ((1<<r)-1)
    if not occupied[Xq]:
        return False
    j = Xq
    runs = 0
    while shifted[j]:
        runs += occupied[j]
        j = left(j)
    while runs > 0:
        j = right(j)
        runs -= not continuation[j]
    while True:
        if R[j] == Xr:
            return True
        j = right(j)
        if not continuation[j]:
            break
    return False

追加

検索でヒットしなかった場合，新たな値$X$を追加する必要がある．
ただし，一般的なハッシュテーブルのオープンアドレスではclusterの最後尾に要素を追加するが，今回は「同じquotientの要素は隣接しなければならない」という制約がある．
そこで，$X$は$X_Q$のrunの最後尾に追加することにする．
そのため，Xを挿入する箇所を$j$として，$j$より右に連続している要素を全て一つ右に移動してから$X$を$j$に保存する．

def insert(x):
    X = hash(x) # 0 <= hash(x) < (1 << p)
    Xq = X >> r
    Xr = X & ((1<<r)-1)
    j = Xq
    runs = 0
    while shifted[j]:
        runs += occupied[j]
        j = left(j)
    while runs > 0:
        j = right(j)
        runs -= not continuation[j]
    while runs == 0:
        if R[j] == Xr:
            return
        j = right(j)
        runs -= not continuation[j]
    k = j
    while shifted[k]:
        k = right(k)
    while j != k:
        shifted[k] = 1
        kl = left(k)
        continuation[k] = continuation[kl]
        k = kl
    R[j] = Xr
    shifted[j] = Xq == j
    continuation[j] = occupied[Xq]
    occupied[Xq] = 1

余談だが，これらのアルゴリズムで現れる演算の多くは，「iより右(左)の最初の1(0)の位置」や，「ある区間の1(0)の数」という演算で表現できるため，簡潔ビットベクトルのrank,select演算を用いて効率化できる．
Pandeyら2の提案した手法は，3つではなく2つのビット列とその簡潔ビットベクトルによってアルゴリズムを実現している．

クエリ性能

Quotient Filterの検索や追加の時間計算量は，各clusterの長さに依存する．
しかし，オープンアドレス法と同様の性質により，データサイズ$n$とバケットサイズ$m=2^q$の比率$\alpha = n / m$が保たれていれば(0.5以下など)，clusterの長さの期待値は$\mathrm{O}(1)$と十分小さくなることから，Quotient Filterの検索，追加は効率的であることが分かる．
細かい解析はオープンアドレス法の解説を参考にして欲しい．

  • Open Data Structures3, Sect. 5.2

偽陽性率

Quotient Filter は値$x$のハッシュ値をそのまま保存するデータ構造である
（$X_Q$はインデックスを元に導出でき，，$X_R$は$R$にそのまま保存している）
ため，偽陽性はハッシュ値が衝突した場合に限り発生する．
よって偽陽性率はハッシュ関数の衝突率と同じになる．

Compact Hash Table

Quotient Filterを少し改良すると，整数値を保存するコンパクトなハッシュテーブルを設計できる．
改良するといっても，データ構造はQuotient Filterをそのまま用いて，hash関数の方を工夫する．

Quotient Filterは，集合の要素のハッシュ値をそのまま保存していた．
ここで，ハッシュ関数が$x$に対して全単射であり，逆関数$\mathrm{ihash}$を持つとき$(\forall x, \mathrm{ihash}(\mathrm{hash}(x))=x)$を考える．
この場合，$X=\mathrm{hash}(x)$を持っていれば，$x=\mathrm{ihash}(X)$が得られる．
つまり，$x$の保存を$X$の保存で代替できる．

よって，任意のデータ型を持つ値に対して逆関数を持つハッシュ関数を準備できるとき，Quotient FilterをHashTableとして利用できる．
逆関数を持つような(双方向な)ハッシュ関数は，例えば乗算ハッシュやXorshift4をベースに設計することが出来る．
Kandaら5の双方向なハッシュ関数の設計では，乗算ハッシュとXorshiftのハイブリッドを用いている．

双方向なハッシュ関数

ここでは双方向なハッシュ関数の例として，乗算ハッシュを用いた方法を紹介する．
入力となる$x$は$p$ビット以下のビット列で表現できる場合を仮定する．
まず，$2^p$以下で**$2^p$と互いに素**な値$z\ (z < 2^p, \gcd(z,2^p)=1)$をランダムに生成し，ハッシュ関数を以下のように定義する．

\mathrm{hash}(x) = x z \mod 2^p

このとき，フェルマーの小定理により，$z$は逆元$z^{-1}\ (zz^{-1} \equiv 1 \mod 2^p)$を持つため，$\mathrm{hash}(x)$の逆関数$\mathrm{ihash}(X)$を定義できる．

\mathrm{ihash}(X) = x z^{-1} \mod 2^p

サイズ

保存する値の型に対して双方向なハッシュ関数が存在する状況を仮定するため，保存する値$x$は全て$p$bit以下で表現できるとする．
例えばハッシュテーブルの負荷率の上限を$\alpha=0.5$としたとき，データ数$n$に対し$2^q \ge 2n \Rightarrow q \ge \lceil\log_2 n\rceil + 1$が条件になる．
ここでは，バケットサイズを必要最小限にするため$q = \lceil\log_2 n\rceil + 1$とする．
一般的なオープンアドレス法によるハッシュテーブルで陽に値を保存すると，要素あたり$p$bitの長さ$2^q$の配列が必要になり，全体で$p2^q=(q+r)2^q$bitである．
一方，Quotient Filterは，3つのビット列と一つのremainder配列で構成されていたため，CompactHashTableは全体で$(3+r)2^q$bitである．
よって，$q > 3 \Rightarrow n > 2^2$ならばCompactHashTableの方がコンパクトになる．

Compact Dynamic Rewritable (CDRW) Array

CompactHashTableを用いて，コンパクトで更新可能な配列CDRW Array6を作れる．
保存する列を$X=x_1,x_2,\dots,x_n$とする．
CDRW　Arrayの考え方は，値$x_i$を表現する最小のビット数が$l$bitならば，$x_i$はそれぞれ$l$bitで保存しようというものだ．

値$x$に対し，$x$を表現するビット数を$\newcommand{\bitlen}[1]{l({#1})} \bitlen{x}$と定義する．
$x$が非負整数ならば$\bitlen{x} = \lfloor \log_2 x \rfloor + 1$である．
ただし，$x=0$なら$\bitlen{x}=1$とする．
また，バケットサイズを$b = \underset{1 \le i \le n}{\max\limits} \bitlen{x_i}$とする．
各値のビット長を保存する配列$\mathrm{bitlen}$を用意し，$\mathrm{bitlen}[i] = \bitlen{x_i}$を保存する．

インデックス$i$をkeyとしてvalue$x_i$を保存する$b$個の連想配列$M_1,\dots,M_b$を用意し，
$\left< i, x_i \right>$は$M_{\mathrm{bitlen}[i]}$に保存する．

$M_j$のkeyの保存はCompactHashTableで表現し，valueは要素サイズ$j$bitの配列を用意してキーと同じ位置に保存する．
keyのbit数は高々$\bitlen{n-1}$bitなので，CompactHashTableのハッシュ値のbit数は$p = \bitlen{n-1} = \lfloor \log (n-1) \rfloor + 1$bitのものを用いれば良い．

サイズ

$\mathrm{bitlen}[i]=j$となる要素数を$n_j$とし，$M_j$のバケットサイズを$Q_j\ \left(n_j/\alpha = (1+\epsilon)n_j \le Q_j < 2(1+\epsilon)n_j \right)$とする．
$M_j$のCompactHashTableのサイズは，$Q_j (3 + p - \log_2 Q_j) \le 2(1+\epsilon) n_j(3 + \Theta(\log n/n_j))$bitとなる．
$N_0=\sum_{i=1}^n \bitlen{x_i}=\sum_{i=1}^n \mathrm{bitlen}[i]$と定義する．
CDRW Array全体のbitサイズ$N$は

\begin{align}
N &\le \overbrace{n (\lfloor \log (b-1) \rfloor + 1)}^{\mathrm{bitlen}} + 2(1+\epsilon)\left\{ {\sum_{j=1}^b n_j\left(3+\Theta(\log n/n_j)\right)} + N_0 \right\} \\
&= n (\lfloor \log (b-1) \rfloor + 1) + 2(1+\epsilon)(N_0 + 3n + \mathrm{O}(nH_0(\mathrm{bitlen}))) \\
&= \mathrm{O}(n \log b + N_0)
\end{align}

である．
ここで$H_0(T)$は列$T$の0次経験エントロピーであり，$T$の値を符号化するときのビット数の期待値の下限を表す．

H_0(\mathrm{bitlen}) = \sum_{j=1}^b \frac{n_j}{n} \log \frac{n}{n_j} \le \log b

CDRW Arrayを提案したPoyasらの論文6では，さらにコンパクトな実装も紹介されている．

ここでは$x_i$を$\bitlen{x_i}$毎のデータ構造で管理する方法を紹介したが，
例えばアクセス速度を向上させるためにバイトアラインメントでそろえて$\lceil \bitlen{b_i}/8 \rceil$毎に管理する，というような実用的な工夫も考えられる．　
データが既知ならば，値の分類方法をデータの値の頻度に合わせて設計しても良い．

  1. Quotient Filter - Wikipedia ↩

  2. P. Pandey, et.al. A General-Purpose Counting Filter: Making Every Bit Count. Proceedings of the 2017 ACM International Conference on Management of Data, pp 775-787, 2017. https://doi.org/10.1145/3035918.3035963 ↩

  3. Open Data Structures ↩

  4. Xorshift - Wikipedia ↩

  5. S. Kanda. et.al. Dynamic Path-decomposed Tries. ACM Journal of Experimental Algorithmics, Volume 25. 2020. Article No.: 1.13, pp 1–28. https://doi.org/10.1145/3418033 ↩

  6. A. Poyas, et.al. Compact Dynamic Rewritable (CDRW) Arrays. 2017 Proceedings of the Meeting on Algorithm Engineering and Experiments (ALENEX). 2017, 109-119. https://doi.org/10.1137/1.9781611974768.9 ↩ ↩2

4
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
4
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?