順序付き集合のシンプルな実装として,スキップリストを紹介します.
※本記事の説明はOpenDataStructuresを参考にしています.
実装はUnlisensedで公開しています.
https://github.com/MatsuTaku/sorted-set-python
順序付き集合
本記事における順序付き集合データ構造は,順序付き集合$S$に対する以下の操作をサポートする.
- $\texttt{find}(x)$: $S$に$x$が存在するなら$x$を,しないなら$\textrm{null}$を返す
- $\texttt{successor}(x)$: $S$の$x$より大きい最小の値を返す
- $\texttt{predecessor}(x)$: $S$の$x$より小さい最大の値を返す
- $\texttt{add}(x)$: $S$に$x$を追加する
- $\texttt{remove}(x)$: $S$から$x$を削除する
例えば,集合$S=\{1,3,6,9,10,13\}$に対するそれぞれの操作は
- $\texttt{find}(10) = 10$
- $\texttt{find}(7) = \textrm{null}$
- $\texttt{successor}(7) = 9$
- $\texttt{predecessor}(7) = 6$
- $\texttt{add}(5)\ (S \leftarrow S \cup \{5\} = \{1,3,\textbf{5},6,9,10,13\})$
- $\texttt{remove}(3)\ (S \leftarrow S \setminus \{3\} = \{1,\ \ 5,6,9,10,13\})$
となる.
また,集合の要素サイズを$n=|S|$とする.
スキップリスト
スキップリストによる順序付き集合は,$S$の$\texttt{add},\texttt{remove},\texttt{successor},\texttt{predecessor}$を期待実行時間$\mathrm{O}(\log n)$で実行する.
スキップリストは,単方向連結リスト$L_0, L_1, \dots, L_{h}$を並べたものと考えられる.
まず,集合の全要素は$L_0$に格納される.
次に$L_1$の要素は$L_0$から一部の要素を取り出して格納する.同様に$L_2$を$L_1$から取り出して格納する.これを繰り返す.
各要素について$L_{r-1}$から$L_r$に格納するかどうかは,コイントスをしてコインが表になるかどうかで決定する.
これを$L_r$が空になるまで繰り返す.
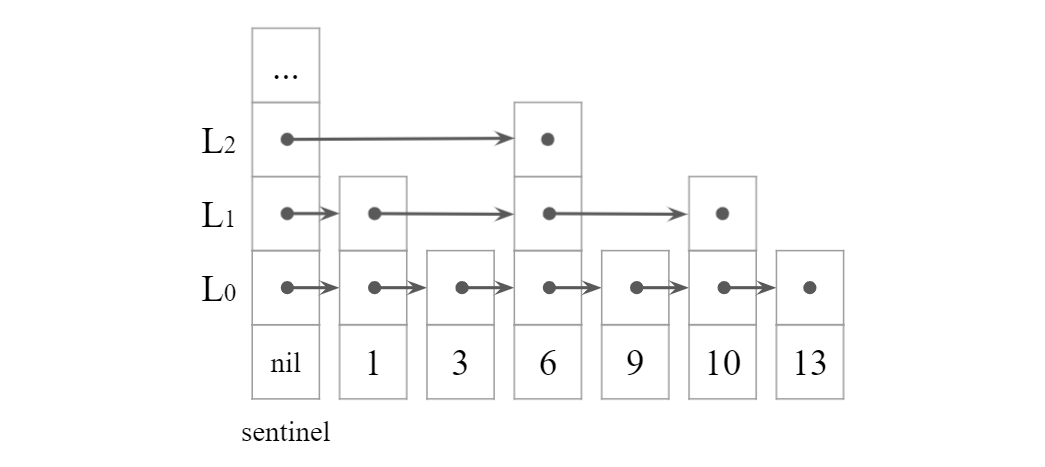
スキップリストの要素$x$について,$x$が格納された$L_r$の添え字$r$の最大値を,$x$の高さと定義する.
各要素の高さは,コイントスを裏が出るまで繰り返したときのコイントスの回数である.
また,スキップリストの各要素の高さの最大値を,スキップリストの高さと定義する.
全てのリストの先頭には**番兵(sentinel)**と呼ばれる要素を用意しておく.
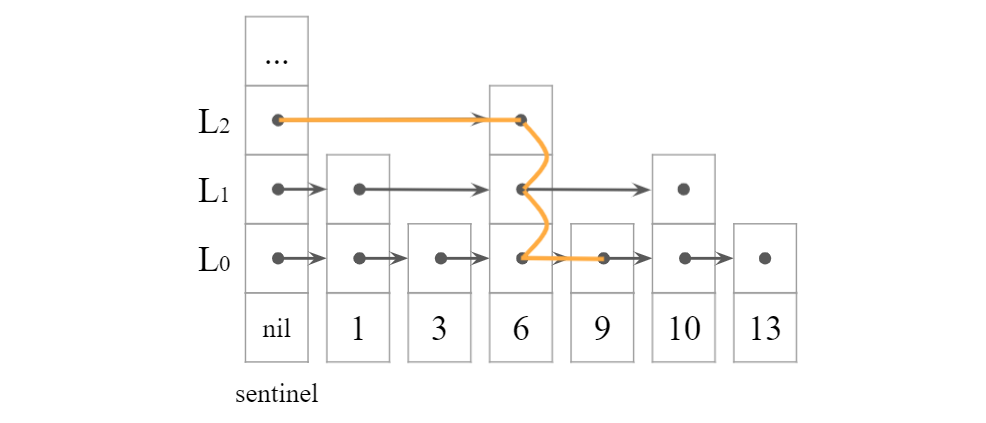
スキップリストにおける要素の探索は,$L_h$の番兵からリンクを辿ることで行う.
$L_h$の番兵から$L_0$の各ノードまでの最短のパスを,探索経路と呼ぶ.
探索経路は以下のように構築できる.
$L_h$の番兵からスタートし,対象のノードリストを右に辿る.
その後現在のノードを一つ下に辿る.これを繰り返す.
例として,$L_0$の要素9までの探索経路を下図に示す.
探索経路の長さの期待値は,以下の補題に示すようにかなり短い.
補題 1:
$L_0$のノード$u$について,$u$の探索経路の長さの期待値は$2\log n + \textrm{O}(1) = \textrm{O}(\log n)$である.
証明
要素$x$の逆探索経路を考える.
この経路は$L_0$における$x$のノードから始まる.
上に向かえるなら上に向かい,そうでなら左へ進む,というパスになる.
ある高さで逆探索経路が通過するノード数は,コインを投げて表が出たら上に向かって停止し,裏が出たら左へ向かって試行を続ける,という試行に関連している.
つまり,ある高さで左へ向かう回数は表が出るまでコイントスを繰り返した回数になる.
その期待値は,$\sum_{i=1}^\infty \frac{1}{2^{i-1}}=1$である.高さ$r$で左に向かう回数を$S_r$とする.
すると$E[S_r] \le 1$である.
さらに,$S_r$は$L_r$の長さを超えることはないので,$S_r \le |L_r|$である.
よって以下が成り立つ.
$$E[S_r] \le E[|L_r|] = n/2^r$$逆探索経路の長さの期待値を考える.
$S$をノード$u$の探索経路の長さとする.
スキップリストの高さを$h$とする.
このとき次の式が成り立つ.
\begin{align} E[S] &= E\left[ h + \sum_{r=0}^h S_r \right] \\ &= E[h] + \sum_{r=0}^h E[S_r] \\ &\le E[h] + \sum_{r=0}^{\lfloor \log n \rfloor} E[S_r] + \sum_{r=\lfloor \log n \rfloor+1}^\infty E[S_r] \\ &\le E[h] + \sum_{r=0}^{\lfloor \log n \rfloor} 1 + \sum_{r=\lfloor \log n \rfloor+1}^\infty n/2^r \\ &\le E[h] + \sum_{r=0}^{\lfloor \log n \rfloor} 1 + \sum_{r=0}^\infty 1/2^r \\ &\le E[h] + \log n + 3 \\ &\le 2\log n + 5 \\ \end{align}この証明は多少行間を省略してるため,より詳しい証明は引用元を参考にしていただきたい.
ノードの空間効率の良い実装は,ノード$u$が値$x$とポインタ配列$\mathit{next}$を持つようにし,$u.\mathit{next}[i]$が$L_i$における$u$の次のリンクを指すようにすれば良い.
こうすると$x$の実体を一つにまとめて管理できる.
class SkiplistNode:
def __init__(self, x, height):
self.x = x
self.height = height
self.next = [None] * (self.height+1)
スキップリストによる順序付き集合
find, successor, predecessor
$\texttt{find}, \texttt{successor}, \texttt{predecessor}$は,それぞれ対象のノードの探索経路を辿ることで達成できる.
これらの演算の計算量は,探索経路の長さで決まるため$\textrm{O}(\log n)$である.
class SkiplistSet:
def __init__(self):
self.sentinel = SkiplistNode(None, MAX_HEIGHT) # 番兵ノード
self.h = 0
self.stack = [self.sentinel] * MAX_HEIGHT
self.length = 0
def __len__(self):
return self.length
def find(self, x):
u = self.sentinel
for r in range(self.h, -1, -1):
while u.next[r] is not None and u.next[r].x <= x:
u = u.next[r]
if u.x == x:
return x
return None
def successor(self, x):
u = self.sentinel
for r in range(self.h, -1, -1):
while u.next[r] is not None and u.next[r].x <= x:
u = u.next[r]
if u.x == x:
break
return u.next[0].x if u.next[0] is not None else None
def predecessor(self, x):
u = self.sentinel
for r in range(self.h, -1, -1):
while u.next[r] is not None and u.next[r].x < x:
u = u.next[r]
return u.x
add
まず考慮するのは,新たに追加する要素の高さを,コイントスの連続によって決定する過程をどのように再現するかである.
これは,ランダムな整数$z$を生成し,$z$の二進数表記において下位bitから連続する1の数を数える1.
from random import randrange
MAX_HEIGHT=32
def pickHeight():
h = 0
z = randrange(1<<MAX_HEIGHT) # 32bitの乱数
while z & (1<<h) != 0:
h += 1
return h
$\texttt{add}(x)$を実装するには,$x$を入れる場所を見つけ,$x$の高さ$k$を$\texttt{pickHeight}$で決め,$x$のノードを$L_0, \dots, L_{k}$に追加する.
これを簡単に実現するため,$x$を入れる場所を見つけると同時に,配列$\textit{stack}$に探索経路を記録しておく.
正確には,探索経路の$L_r$から$L_{r-1}$に下がるときの$L_r$のノードを$\textit{stack}[r]$に記録する.
こうすると,修正が必要なノードは$\textit{stack}[0], \dots, \textit{stack}[k]$になる.
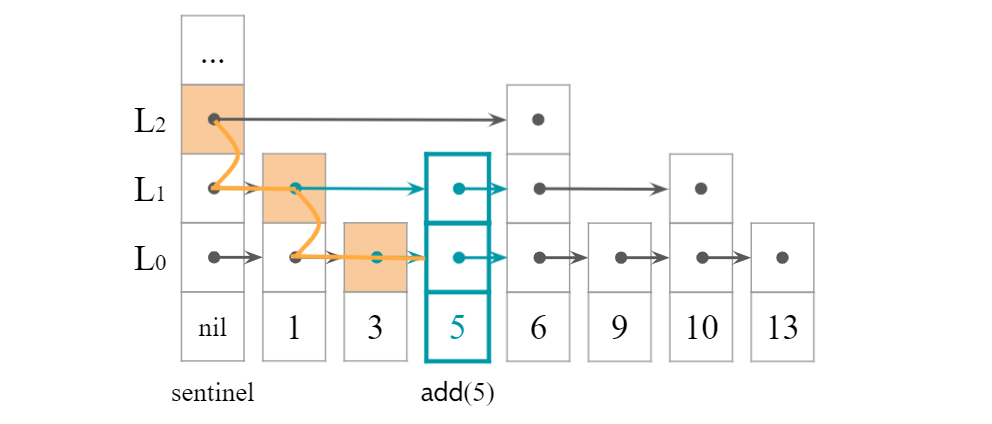
class SkiplistSet:
...
def add(self, x):
u = self.sentinel
for r in range(self.h, -1, -1):
while u.next[r] is not None and u.next[r].x < x:
u = u.next[r]
if u.next[r] is not None and u.next[r].x == x:
return
self.stack[r] = u
w = SkiplistNode(x, pickHeight())
if self.h < w.height:
self.h = w.height
for i in range(w.height+1):
w.next[i] = self.stack[i].next[i]
self.stack[i].next[i] = w
self.length += 1
remove
$\texttt{remove}(x)$も$\texttt{add}$とほぼ同様だが,ノードの修正は削除するノードの探索と同時に行う.
正確には,$x$の探索途中で$L_r$から下に向かうとき,現在のノード$u$の右のノードの値が$x$なら$u.\textit{next}[r] \leftarrow u.\textit{next}[r].\textit{next}[r]$と継ぎ変える.
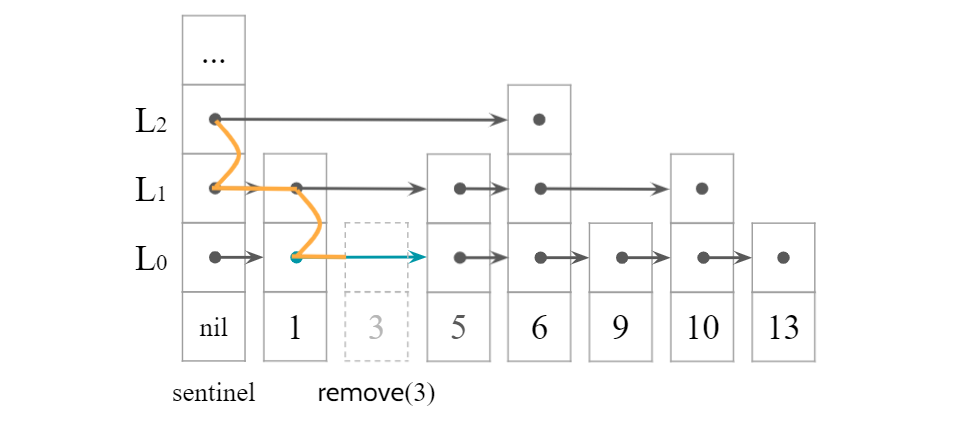
class SkiplistSet:
...
def remove(self, x):
u = self.sentinel
removed = False
for r in range(self.h, -1, -1):
while u.next[r] is not None and u.next[r].x < x:
u = u.next[r]
if u.next[r] is not None and u.next[r].x == x:
removed = True
u.next[r] = u.next[r].next[r]
if (u.x is None # When u is sentinel
and u.next[r] is None):
self.h -= 1
if removed:
self.length -= 1
あとがき
順序付き集合の実装として最も知られているのは平衡二分探索木です.
しかし平衡二分探索木は少し複雑で,コード量も多くなります.
一方で,スキップリストを用いた実装は比較的単純で,これをベースにした新たなデータ構造を設計する際にもコーディングのコストを抑えることができます.
順序付き集合の実装においてスキップリストが平衡二分木に劣る点は,スキップリストは乱数を用いて設計されており,クエリ実行時間が確率的になるということです.
即ち,一部の値に対するクエリ実行時間が非常に長くなる可能性があります.
一方で,平衡二分探索木は全てのクエリの短時間での実行が保証されます2.
これが多くの標準ライブラリで平衡二分木が採用される理由です.
本記事を書いたきっかけについてです.
先日,競技プログラミングサイトAtCoderで,順序付き集合の$\texttt{add},\texttt{successor},\texttt{predecessor}$を用いることを想定とした問題が出題されました.
ABC217 - D - Cutting Woods
この問題の正解率が,順序付き集合データ構造が容易に利用できる言語とそうでない言語(Pythonなど)で差が出たことで,競プロにおける言語選択の影響が話題になりました.
しかし,その実装として挙げられるものの殆どが平衡二分木についてであり,認識を必要以上に複雑にしていると感じたため,順序付き集合の実装のバリエーションについて紹介しておこうと考えました3.