中心極限定理は「標本の平均値の分布」に注目したもの!
混乱しやすいが重要な点は、中心極限定理とは、標本の個々のデータについてのものではなく、**たくさんの標本データのそれぞれの「標本平均」をかき集めた「標本平均の分布」についてのものであるということ!
そこからさらに、「「標本平均の分布」の平均、分散(標準偏差)」**について考える。

中心極限定理とは以下のようなことである。
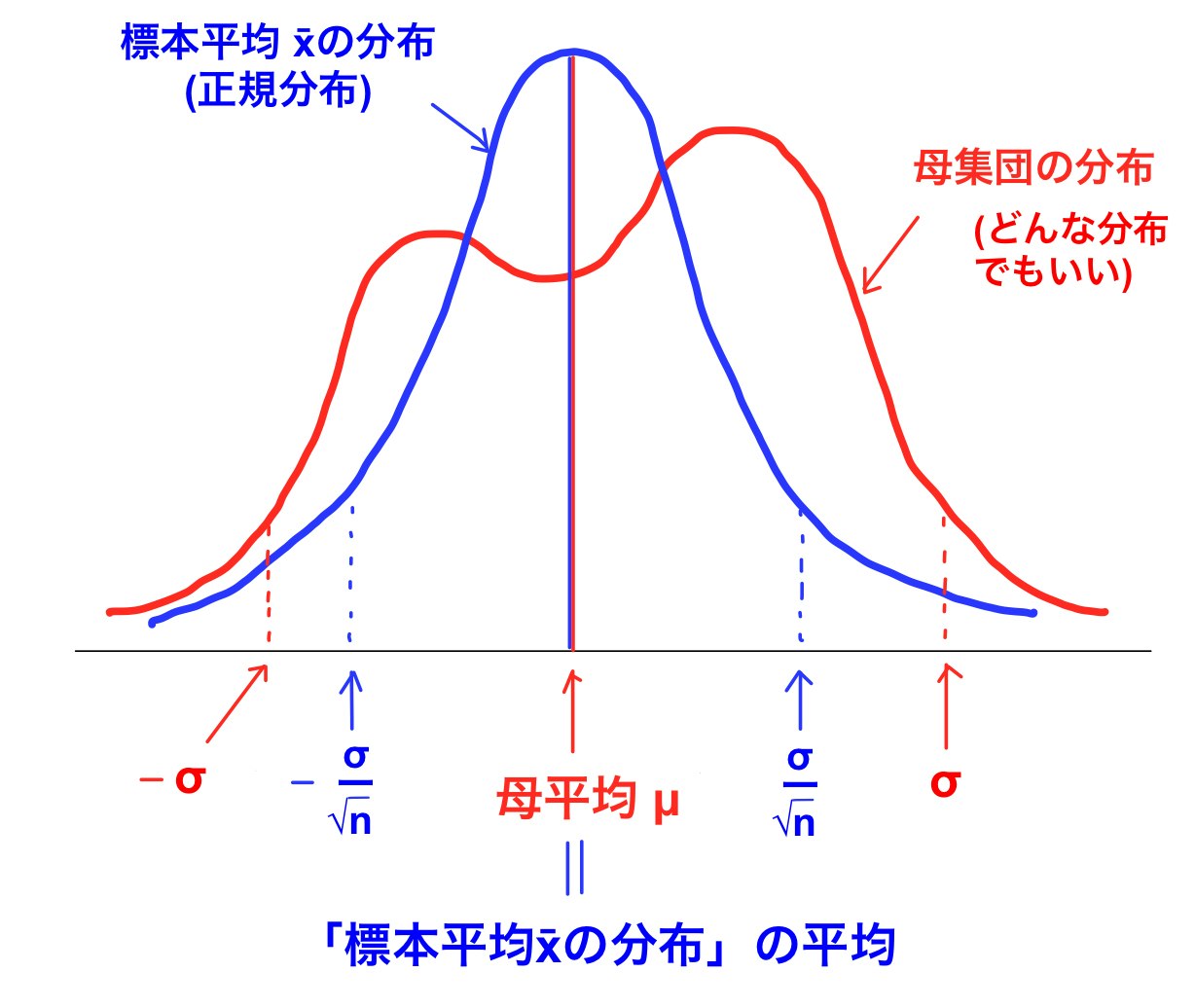
(1)「「標本平均$\bar{x}$の分布」の平均」は「母集団の平均(μ)」と一致する
(2)「「標本平均$\bar{x}$の分布」の分散」= $\frac{σ^2}{n}$(σ:母集団の標準偏差)
(3) 母集団がどのような分布でも、サンプル数nが大きくなるにつれ「標本平均$\bar{x}$の分布」は正規分布に近づく
あるデータの分布を知りたいとき、「平均」と、それを中心にどれだけずれがあるかの「標準偏差」が分かれば、分布の特徴がつかめる。
(1)より標本平均**$\bar{x}$の分布の平均がわかる。
(2)より、標本平均$\bar{x}$の分布の標準偏差はわからなくても、母集団の標準偏差(σ)が分かっていれば、$\frac{σ^2}{n}$**で代用できることがわかる。分母に標本数nがあるので、標本が大きくなるほど分散が小さくなり、母集団の分布に近づいていくことがわかる。