４点の関節座標から意図する角度を求める【function編】 #MATLAB

本記事の概要

2つのベクトルが成す角度、といえば内積などを利用して簡単に求められそうです。
ときにその鋭角を求めるだけでは済まない場合があり、条件分岐で頭もコードも大混乱になりました。
本記事では、そんな私が行きついた条件分岐をほぼゼロにした解決策をお伝えします。

長くなりますので、function編、OpenPose編に分けて投稿します。

本記事はfunction編です。

本記事のターゲット

角度の算出に困っている方
特に動作分析における関節角度の算出に困っている方
既に算出できていて、この記事の方法より優れた手法をご存知の方

経緯

ここで扱うのは、２つのベクトルの成す角です。
（実際には右を向くヒトの足関節背屈角度を求めようとしていました。）

一般的な角度算出方法

一般に、原点O、点A、点Bからなる∠AOBは以下の式で求められます。

θ = arccos (\frac{x_A x_B + y_A y_B}{|A||B|})

この式はベクトルA、ベクトルBのx, y成分とも考えられますね。

今回のサンプルデータ

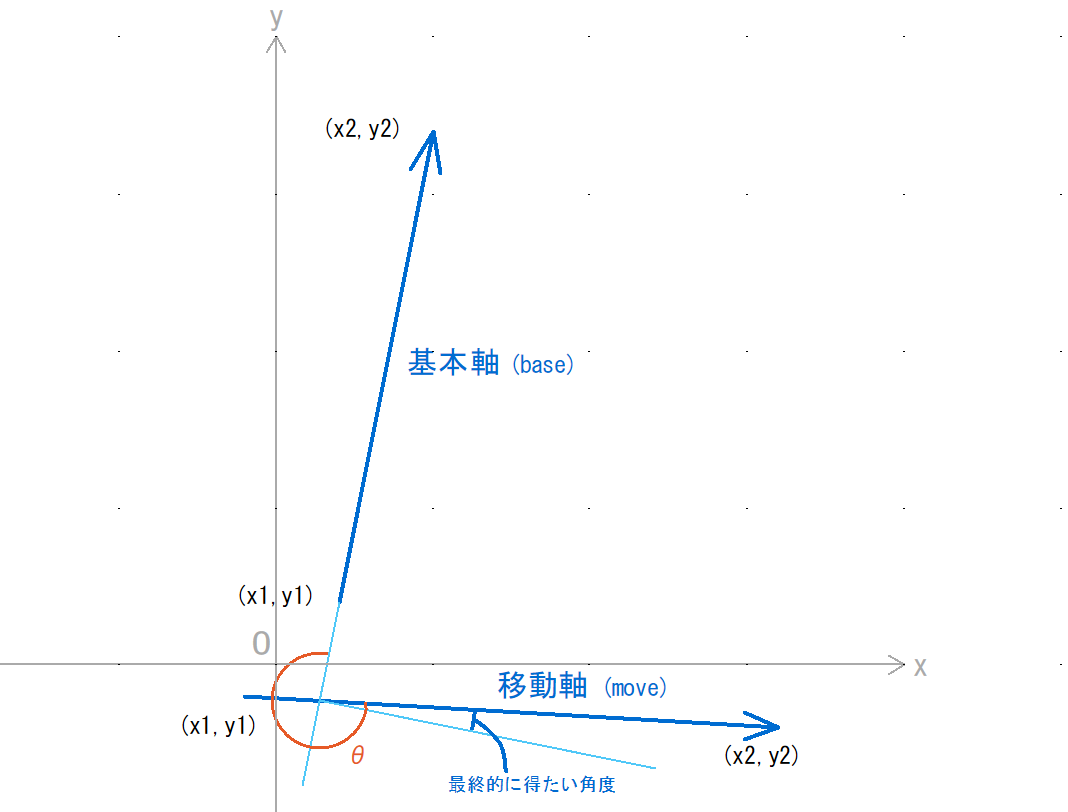
ここではそれぞれのベクトルを基本軸(base)、移動軸(move)とします。
（関節可動域は基本軸と移動軸の位置関係ですので、線分でなくベクトルで考える必要があります。）

ここで問題なのは、上の式で求められる角度は180°以下であることです。
足関節ならあまり問題はありませんが、肩関節屈曲-伸展などの広い可動域を持つ関節では屈曲180°以上や伸展域を適切に求めるための条件分岐が煩雑です。

肩関節矢状面角度算出時の条件分岐の例

求めた角度を以下の３つのケースに場合分けして調整する必要があります。

屈曲 0°～180°

屈曲 180°～

伸展域

基本軸と移動軸の位置関係で条件分岐できますがコードが煩雑になります。
さらに肩関節でも内-外転、また他関節の角度を求めるとなると、各関節角度算出時に条件分岐が必要で面倒です。

私は最初、条件分岐で１１関節角度を求めるコードを書いたところコードは600行まで膨らみました...

本funuctionの有用性

行きついたのは、常に基本軸から移動軸へ時計回りの角度を求めることでした。
「時計回り」と固定するのがミソです。

追加で関節角度を求めようとする際、この手法を使えば関節角度の追加算出ひとつにつきコード１行の追加で済みます。いわば、煩雑だった条件分岐を無くす手法です。

角度を求めるfunction

今回はMATLAB言語で書くこととします。

入力する座標を準備

構造体で整理しつつ座標を定義します。（上図と対応させます）

    base = struct ('x1', 2, 'y1', 2, ...
                    'x2', 5, 'y2', 17);
    move = struct ('x1', 1, 'y1', -1, ...
                    'x2', 16, 'y2', -2);

MATLAB初学者にはこの記法のほうが分かりやすいか

base.x1 = 2;
base.y1 = 2;
base.x2 = 5;
base.y2 = 17;

move.x1 = 1;
move.y1 = -1;
move.x2 = 16;
base.y2 = -2;

functionと使用例

function result = coo2angle (base, move)

      q.tmp = [11; 1; 0; 10];  % 象限No. [1, 2, 3, 4]
      q.k.base = [0,1; -1,0; 0,-1; 1,0];  % 基本軸部の角度算出時の係数
      q.k.move = [1,0; 0,1; -1,0;  0,-1];  % 移動軸部の角度算出時の係数

      base.tmp = ((base.x2 - base.x1) > 0)*10 + ((base.y2 - base.y1) > 0);
      move.tmp = ((move.x2 - move.x1) > 0)*10 + ((move.y2 - move.y1) > 0);

      % 角度算出は、関節座標に欠損値が含まれる場合にはスキップ（そのフレームでは関節座標を算出しない）
      if ~any (isnan ([base.tmp, move.tmp]))

            base.quadID = find (q.tmp==base.tmp, 1);
            move.quadID = find (q.tmp==move.tmp, 1);
            quadBetw = mod (move.tmp - base.tmp, 4);  % 基本軸～移動軸でいくつの象限をまたいでいるか

            % 基本軸から、反時計回りにその象限の境界までの角度
            k = q.k.base(base.quadID, :);
            angle.base = acosd (((base.x2 - base.x1) * k(1) + (base.y2- base.y1) * k(2)) ...
                                    / sqrt((base.x2 - base.x1)^2 + (base.y2- base.y1)^2));
            clearvars k;

            % 移動軸から、時計回りにその象限の境界までの角度
            k = q.k.move(move.quadID, :);
            angle.move = acosd ((k(1) * (move.x2 - move.x1) + k(2) * (move.y2- move.y1)) ...
                                    / sqrt((move.x2 - move.x1)^2 + (move.y2- move.y1)^2));
            clearvars k;

            angle.betw = (quadBetw - 1) * 90;  % 基本軸～移動軸の間にある象限の数 *90

            % ここまで３つに分けて算出した角度を合算
            result = mod (angle.base + angle.betw + angle.move, 360);  % 負にならないようにmod
      else
            result = nan;
      end
end

使用例

先に定義した変数base, moveを、自作関数coo2angleの引数にして実行します。
（base, moveを構造体にしたのは、計8つの座標をfunctionの引数に指定すると長ったらしいからです。）

result = coo2angle (base, move);
disp (result);
  277.4959

上の図の橙θ部分を277.4959と求められました。
この角度は時計回りですので負になりません。（0 ≦ result < 360）

function内部の解説

それぞれ象限の取得

base.tmp = ((base.x2 - base.x1) > 0)*10 + ((base.y2 - base.y1) > 0);
move.tmp = ((move.x2 - move.x1) > 0)*10 + ((move.y2 - move.y1) > 0);

基本軸ベクトル・移動軸ベクトルが、始点を原点に平行移動させた際に終点がどの象限にあるかを調べています。
式の通り、十の位がx、一の位がyに対応しています。
例えば、base.tmp == 1の場合は第４象限、base.tmp == 11の場合は第１象限に対応しています。
もし式に含まれるそれぞれ４つの座標のうち１つでもnanがあれば、それぞれの値はnanになります。

今回の例

disp (base.tmp);
  11
disp (move.tmp);
  1

基本軸と移動軸の位置関係を取得

q.tmp = [11; 1; 0; 10];  % 象限No. [1, 2, 3, 4]

base.quadID = find (q.tmp == base.tmp, 1);
move.quadID = find (q.tmp == move.tmp, 1);
quadBetw = mod (move.tmp - base.tmp, 4);

q.tmpは、角度を時計回りに求めるための、象限の順序を規定する変数です。
base.quadIDは、基本軸の象限がq.tmpの何番目にあるかを示します。
move.quadIDは、移動軸の象限がq.tmpの何番目にあるかを示します。
quadBetwは、移動軸の象限が基本軸の象限のいくつ先にあるかを示します。先なので、負にならないようにmodで正にしつつ時計回りを保っています。

今回の例

disp (base.quadID);
  1
disp (move.quadID);
  4
disp (quadBetw);
  3

それぞれ象限内での角度を算出

q.k.base = [0,1; -1,0; 0,-1; 1,0];  % 基本軸部の角度算出時の係数
q.k.move = [1,0; 0,1; -1,0;  0,-1];  % 移動軸部の角度算出時の係数

% 基本軸から、反時計回りにその象限の境界までの角度
k = q.k.base(base.quadID, :);
angle.base = acosd (((base.x2 - base.x1) * k(1) + (base.y2- base.y1) * k(2)) ...
                    / sqrt((base.x2 - base.x1)^2 + (base.y2- base.y1)^2));
clearvars k;

% 移動軸から、時計回りにその象限の境界までの角度
k = q.k.move(move.quadID, :);
angle.move = acosd ((k(1) * (move.x2 - move.x1) + k(2) * (move.y2- move.y1)) ...
                    / sqrt((move.x2 - move.x1)^2 + (move.y2- move.y1)^2));
clearvars k;

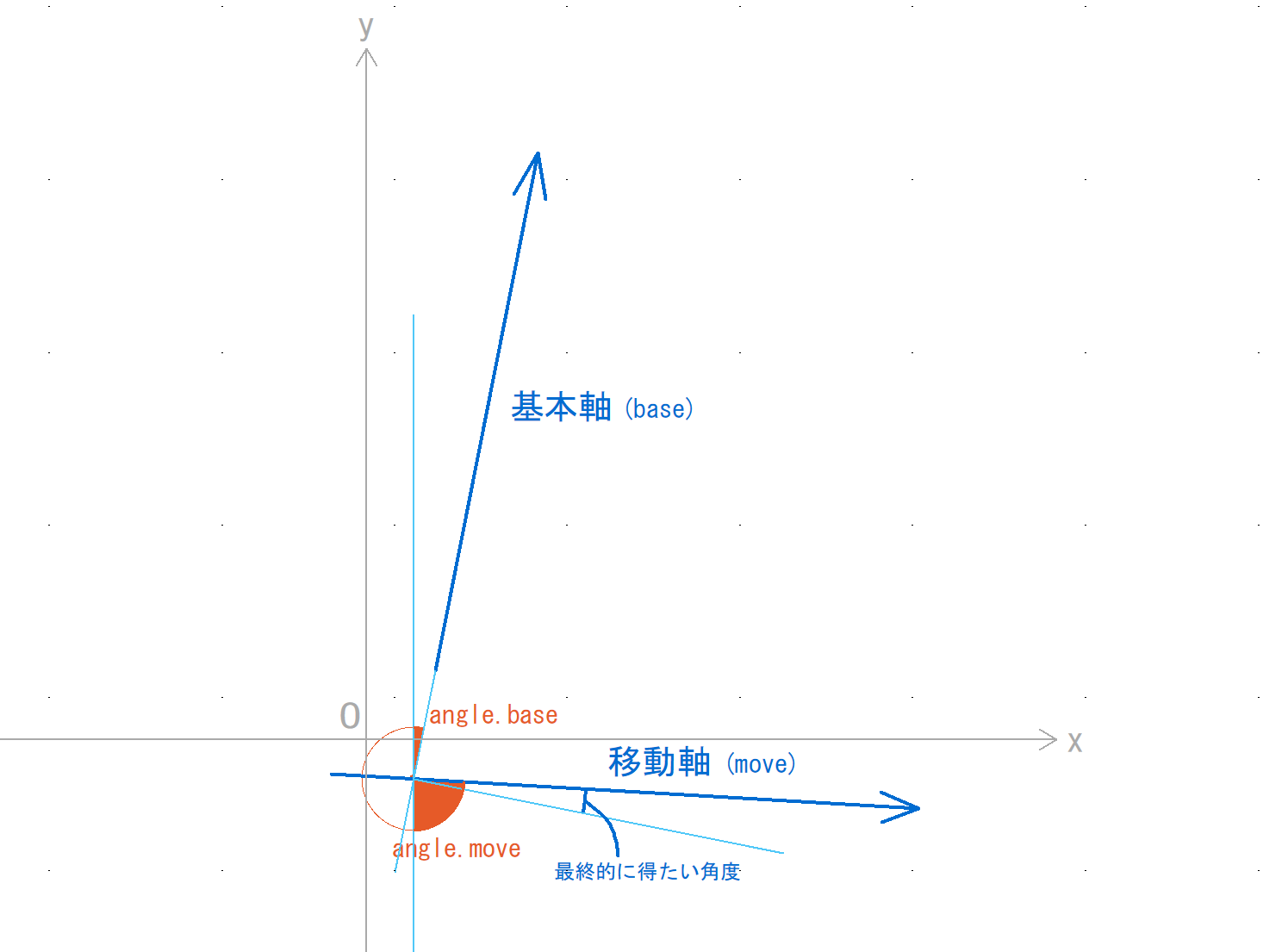
angle.baseは、象限内の基本軸からの時計回りの角度を示します。
angle.moveは、象限内の移動軸までの時計回りの角度を示します。

q.k.base q.k.moveおよびkの解説は、少し煩雑ですので以下トグル内を参照ください。

係数の解説

座標から鋭角を求める式は以下のものでした。
θ = arccos (\frac{x_A x_B + y_A y_B}{|A||B|})
基本軸部の角度（angle.base）

ベクトルBを以下になるように定義します。

始点：基本軸の始点と同じ

終点：基本軸から時計回りでの象限の境界

長さ：1

このとき、ベクトルBの成分は基本軸の存在する象限により４通りあります。
q.k.base = [0,1; -1,0; 0,-1; 1,0];  % 基本軸部の角度算出時の係数
k = q.k.base(base.quadID, :);
q.k.baseはこの際のx_B, y_Bに対応しています。
base.quadIDは、基本軸がどの象限にあるかを示すものでした。
これらをもとにx_B, y_Bであるkを求めます。
またベクトルBの長さは1になるので、分母も簡潔になります。

移動軸部の角度（angle.move）

基本軸部とほぼ同じですが、移動軸部ではベクトルAを定義します。

clearvars k;はそれぞれの角度算出時にkを上書きするので省略できますが、同じ変数名を使っているため可読性向上とエラー回避のために実行しています。

今回の例

disp (angle.base);
  11.3099
disp (angle.move);
  86.1859

基本軸象限と移動軸象限の間の角度を算出

angle.betw = (quadBetw - 1) * 90;  % 基本軸～移動軸の間にある象限の数 *90

quadBetwは、移動軸象限と基本軸象限の差を示し、[0, 1, 2, 3]のいずれかです。
quadBetwとangle.betwは以下のように対応します。

`quadBetw`	`angle.betw`
0	-90
1	0
2	90
3	180

ここで、quadBetw == 0つまり２つの軸が同じ象限にある場合を説明します。
このとき２つのケースがあります。

ケース１：0 ≦ angle.betw < 90
ケース２：270 ≦ angle.betw < 360

しかしこれらの条件分岐は、次のステップでのmodにより解消できます。

今回の例

disp (angle.betw);
  180

３つの角度を合計

result = mod (angle.base + angle.betw + angle.move, 360);

３つに分けて算出した角度を合計します。
この際、前のステップで問題になっていた箇所は、modで負にならないようにすることで解消できます。

次回予告

本記事で紹介した自作関数coo2angleで、関節角度を求めてみます。
一部先出しすると、右向きのヒトの股関節屈曲角度はcoo2angle(base, move) - 180;となります。
関数coo2angleの恩恵により、求める角度によりこのように式を調整するだけで済み、細かい条件分岐が不要です。

余談

自作関数coo2angle内にはひっそりと条件分岐が３つあります。
うち２つはmodにより、１つはq_tmpを軸としたfindにより、ifやswitchの登場無く実行できます。
そのぶん処理実行時間はわずかに短縮できています。
やや可読性は劣りますが、シンプルにする方法として私はよく使います。

また本記事と次回で紹介するコードは、11関節の座標を求めるものとして、初稿の600行から改良して100行強にまで簡潔にさせたものです。

以上、初投稿でしたが次回の記事も近々挙げますので、ご意見ございましたらお寄せください！

４点の関節座標から意図する角度を求める【function編】

本記事の概要

本記事のターゲット

目次

経緯

一般的な角度算出方法

今回のサンプルデータ

本funuctionの有用性

角度を求めるfunction

入力する座標を準備

functionと使用例

使用例

function内部の解説

それぞれ象限の取得

基本軸と移動軸の位置関係を取得

それぞれ象限内での角度を算出

基本軸部の角度（angle.base）

移動軸部の角度（angle.move）

基本軸象限と移動軸象限の間の角度を算出

３つの角度を合計

次回予告

余談