はじめに
「世界一わかりやすく」とか言っとけばいいねもらえると思っている安易なネーミングをお許しください。
みなさん今日も機械学習お疲れ様です。桜も散りそうですがいかがお過ごしでしょうか。
さて、桜といえば、目黒川の夜桜がめちゃくちゃキレイでした。実は今回は全く桜の話ではないですけどね。
クラスタリング
さて、機械学習している人なら誰でも一度は嗜んだであろう「クラスタリング」ですが、みなさんはまず「教師なし学習」と聞いて
「なにか強大な力が働いていそう」
なんて思ったんじゃないでしょうか?
それで勉強していったらscikit-learnなんていう便利なライブラリに早々に出会い、「便利じゃん」とかいって中身を何も理解せずに機械学習している。違いますか?
まだ間に合います。今ここで「教師なし学習」の中身を完全に理解しましょう。
大丈夫。強大な力なんてどこにもありません。数学くらいは知っておいてほしいですけど。
概要
そもそもクラスタリングというのは、データにラベルを与えることを言います。
正解も何もない生のデータを分類していくから「教師なし学習」なんて呼ばれています。
アルゴリズム
さて、具体的にデータをクラスタリングしていきましょう。
僕は親切なので、ここに来るみんなが書籍などでクラスタリングのアルゴリズムを理論的に勉強するのが億劫なことくらい知っています。
文字がバーーーってなってても何がなんだかわからないと思うので実際に2次元の生データをプロットしてクラスタリングの推移を見ていきたいと思います。
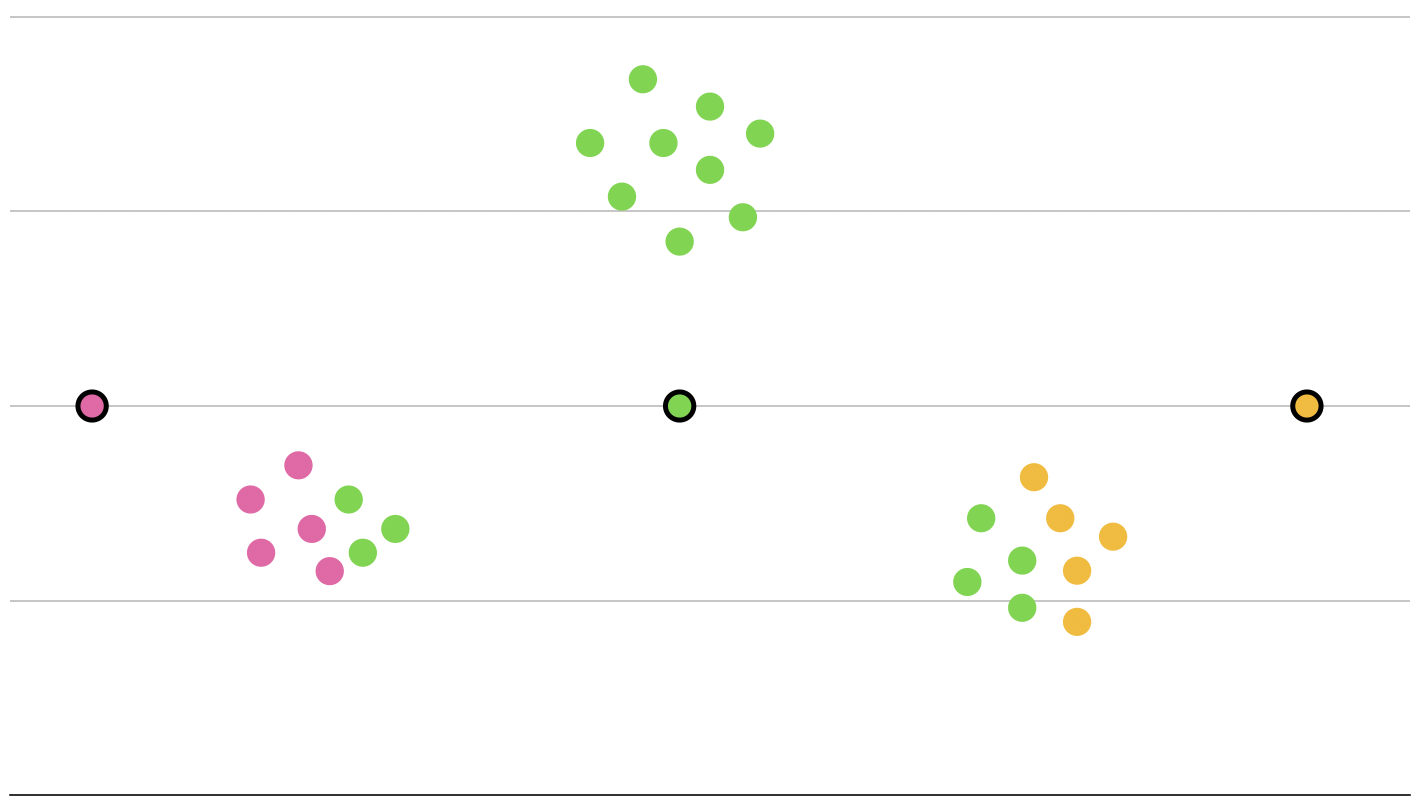
さて、下のようなデータがあります。
人間なら、これを3種類に分類することはたやすいでしょう。
しかし、機械がこれをどう分類するか想像することはたやすくないことでしょう。
さあ、まず機械は、分類の重心となる点を適当に生成します。これをセントロイドなんて呼んだりもします。
次にそれぞれのデータとの距離を計算します。
ここでいう「距離」ですが、一般的にはユークリッド距離を指します。
なんか難しいなあって思った人、大丈夫、ただの距離だから。三平方の定理だから。
イメージにすると本当にこんな感じで、純粋な距離を指していることがわかりますね。
対して、マンハッタン距離なんてのもあります。今回は使いませんがこの際なので覚えておきましょう。
この2つの距離の概念は教師あり学習の回帰なんかでうるさくやります。実はけっこう大事だったりもします。
さて、早速分類していきますが、このユークリッド距離を計算し、一番近いものを自身のラベルと判定します。
ね??簡単でしょ??普通でしょ??
さすがにこれで終わったらポンコツすぎるのですごいのはここから。
ラベル付けされたデータの重心に中心となる点を移動させます。ベクトルを勉強した人なら簡単だと思いますが重心はこんな感じでチョチョイのチョイで求められます。
$$
\vec{G}=\frac{\sum_{k=1}^{n}{\vec{a_k}}}{n}
$$
ベクトルがよくわからない人はこれを座標に置き換えればオッケーです
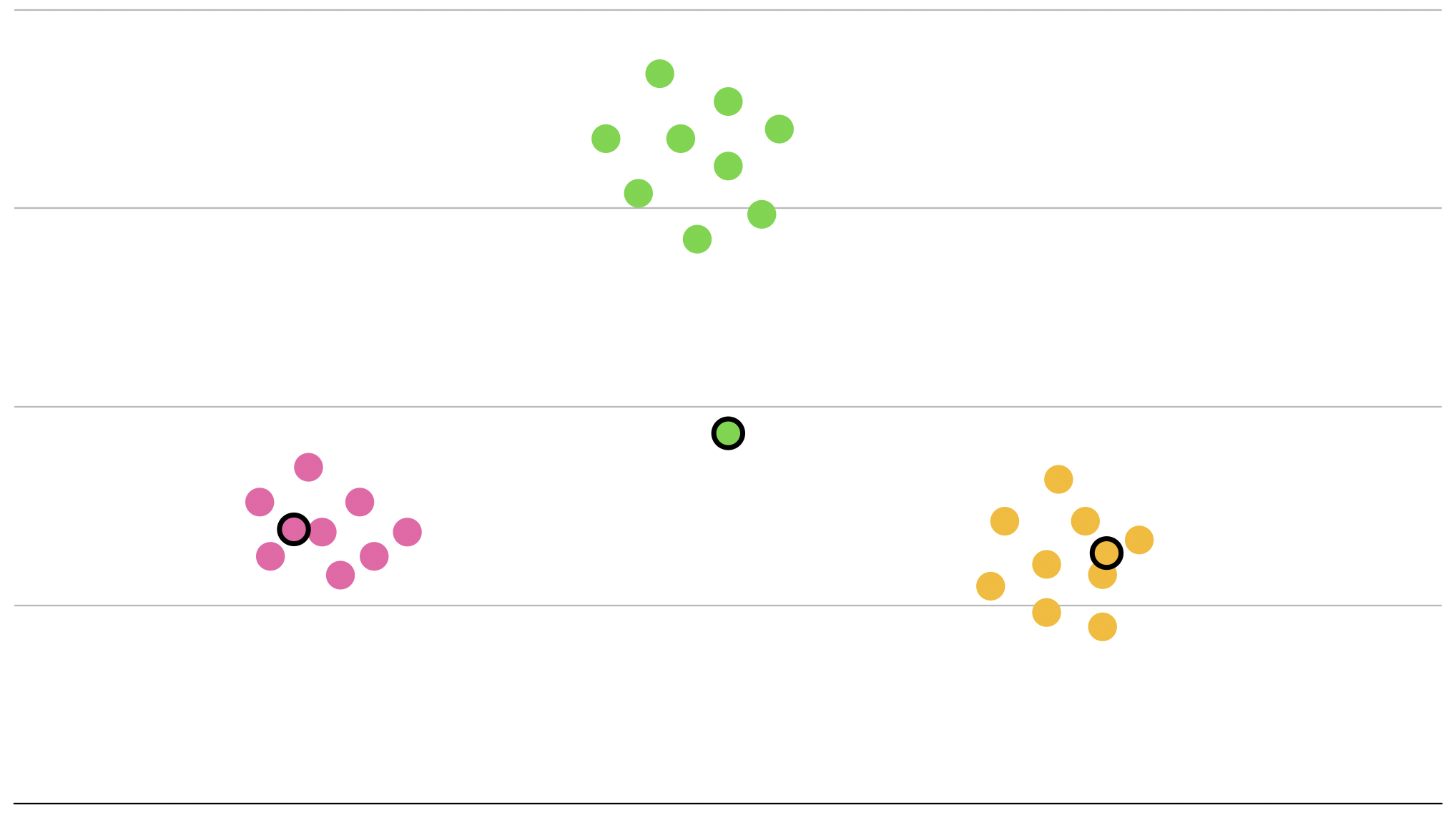
さて、そうしてセントロイドを移動させました。
ここでもう一度ユークリッド距離を計算し直して再度ラベル付けを行います。
あら不思議、もう立派に分類がされています。
最後に重心も計算し直してセントロイドを正確な位置に移動させれば...
完成です!!
お察しの通り、セントロイドをランダムに配置することが肝心で、このセントロイドを上手い具合に動かしていくことによって分類を実現させています。
アルゴリズムをまとめます。
クラスタリングのアルゴリズム
- k(≥1)を決めます
- k個のランダムな配列(セントロイド)を生成します
- セントロイドからの距離を近いものにラベル付けしていきます
- 各ラベルの重心にセントロイドを移動させます
- セントロイドが収束するまで3, 4を繰り返します
次回、実装。
実装
では、やっていきます。
決して難しくありませんがゴチャゴチャしてくると嫌なので計算の中身はnumpyに任せました。
まず、セントロイドの生成から。
import numpy as np
# kはクラスターの数、arrは生データを指しています
centroids = np.random.randint(np.max(arr), size=(k, arr.ndim))
データセットが2次元とは限らないことも考慮しています。
次にラベル付け。
ユークリッド距離を計算して一番ユークリッド距離の短いラベルにクラスタリングします。
labels = []
# データの1つ1つを精査
for index, data in enumerate(arr):
min_distance = 10000000 # なるべく大きい数
min_label = 0
# セントロイド一つ一つと精査
for cluster, centroid in enumerate(centroids):
eucrid_distance = np.linalg.norm(data - centroid, ord=2)
if min_distance > eucrid_distance:
min_distance = eucrid_distance
min_label = cluster
labels.append(min_label)
そして重心の計算と移動。
# 更新後のセントロイド(初期化のためにそのまま代入)
centroids_new = centroids
for cluster in range(k):
# 重心(原点で初期化。後の計算のためにfloat型に)
gravity_center = np.array([0, 0], dtype=np.float)
# クラスターごとに重心を再計算
for index, label in enumerate(labels):
# 重心の計算
if label == cluster:
gravity_center+= arr[index] / len(arr)
# セントロイドを更新
centroids_new[cluster] = gravity_center
さて、ここで、なぜcentroidsとcentroids_newを分けたのかと気になる方が出てくるでしょう。
それは、アルゴリズムの
セントロイドが収束するまで
の「収束」を機械的にハッキリさせるために移動距離を比較したいからです。
具体的な比較方法は様々ですが3歳のパイソニアでもわかるよう以下のようにしましょう。
er = []
for cluster in range(k):
# 移動距離を計算(これもユークリッド距離)
centroid_error = np.linalg.norm(centroids_new[cluster] - centroids[cluster], ord=2)
er.append(centroid_error)
# 距離が収束していないと判断した場合セントロイドを更新してもう一回前の作業を行います
if np.mean(er) < error:
centroids = centroids_new
continue
break
最後に、クラスタリング終了後の返り値を定義します
return labels, centroids_new
本当にたったこれだけ。簡単でしょ?
実はscikit-learnはこれを上手いことやっています。機会があればその仕組みを見ていきましょう。
とりあえず今回はここまで。コードはGitHubにあげてます。