はじめに
この記事は、私がRで共分散構造分析を行うにあたり調べた事や、実際に分析する過程で得た知見をまとめたものです。Rで共分散構造分析をする方法は共分散構造分析 R編という本によくまとまっているのですが、sem()の実行結果の詳細や不適解の対処法などはこの本に載っていなかったので、この記事を作成しました。
この記事を書くにあたり、先ほども出た共分散構造分析 R編という本を大きく参考にしました。個人的には、Rで共分散構造分析をやり始めるなら、とりあえずこの本を見ると良いと思います。この記事も、この本を見たりした後実際に分析をしていく時に参考になるのではないかと思います。
間違っている所などありましたらコメント等をお願いします。
説明の都合上、モデルを改良 節までは、それ以前の節で作成した変数(model、fit)を使うことがあります。
前提
ライブラリ
この記事で使用するライブラリは次の通りです。
library(psych)
library(semTools)
library(semPlot)
library(gplots)
インストールされていないライブラリは次のコマンドでインストールできます。
install.packages('psych') # psychがインストールされます
各ライブラリの用途は次の通りです。
-
psychは探索的因子分析を行う時に使用します。 -
semTools、semPlot、gplotsは共分散構造分析で使用します。semToolsを介して lavaan という共分散構造分析ライブラリを使用します。
データセット
この記事では lavaan に含まれている PoliticalDemocracy データセットを使用します。
X <- PoliticalDemocracy
このデータセットには、発展途上国における民主政治(y)と工業化(x)の各種指標の値が含まれています。具体的には次の通りです。
| 変数名 | 意味 |
|---|---|
| y1 | 1960年の報道の自由に関する専門家の評価 |
| y2 | 1960年の政治的反対の自由 |
| y3 | 1960年の選挙の公平性 |
| y4 | 1960年に選出された立法府の有効性 |
| y5 | 1965年の報道の自由に関する専門家による評価 |
| y6 | 1965年の政治的反対の自由 |
| y7 | 1965年の選挙の公平性 |
| y8 | 1965年に選出された立法府の有効性 |
| x1 | 1960年の一人当たりの国民総生産(GNP) |
| x2 | 1960年の一人当たりの無生物のエネルギー消費量 |
| x3 | 1960年の産業における労働力の割合 |
共分散構造分析
共分散構造分析の概要
共分散構造分析(Covariance structure analysis, CSA)は変数間の関係を調べる統計手法です。構造方程式モデリング(Structual equation modeling、SEM)とも呼ばれます。
共分散構造分析では例えば次の様な事が出来ます:国語・数学・理科・社会の4教科の試験の結果を元に、「文系力」や「理系力」といった能力を仮定して、点数との関連を調べる。
共分散構造分析で行う事
共分散構造分析の概要をこのスライドに短くまとめてみました。スライドの内容を要約するとこんな感じです:
- 変数は3種類:観測変数、誤差変数、潜在変数
- 手順は4ステップ:測定方程式を立てる → 構造方程式を立てる → 共変関係を仮定 → 係数、共変関係(誤差変数間の共分散)、 誤差分散、誤差変数を仮定していない潜在変数・観測変数の分散、を推定
(潜在変数を仮定しないで共分散構造分析をする事も可能です。この場合は、観測変数間の関係を調べます。)
変数の名称
共分散構造分析では観測変数、誤差変数、潜在変数の3種類の変数が登場しますが、これらをさらに大きな括りでまとめて呼称する事もあります。
- 観測変数と潜在変数はまとめて構造変数と呼ばれます。
- 変数にパスが刺さっている変数を内生変数と呼び、そうでない変数を外生変数と呼びます。このスライドなら
f1以外が内生変数でf1が外生変数です。
lavaanにおけるモデルの記述方法
PoliticalDemocracy データセットに対して次のモデルを当てはめます。このモデルはlavaan の公式チュートリアルに掲載されています。
ind60、dem60、dem65が潜在変数です。ind60が1960年の工業化の度合いを表し、dem60とdem65はそれぞれ1960年、1965年の民主政治の度合いを表します。
後で使用するのでmodelという変数に文字列として格納しておきます。
model <- '
# 測定方程式
ind60 =~ x1 + x2 + x3
dem60 =~ y1 + y2 + y3 + y4
dem65 =~ y5 + y6 + y7 + y8
# 構造方程式
dem60 ~ ind60
dem65 ~ ind60 + dem60
# 共変関係
y1 ~~ y5
y2 ~~ y4 + y6
y3 ~~ y7
y4 ~~ y8
y6 ~~ y8
'
各変数の分布(正規性)を確認
共分散構造分析の推定法は、観測変数の正規性(変数が正規分布に従っているか)の程度に応じて変わります。そのため、調べておくと良いはずです。
ヒストグラム
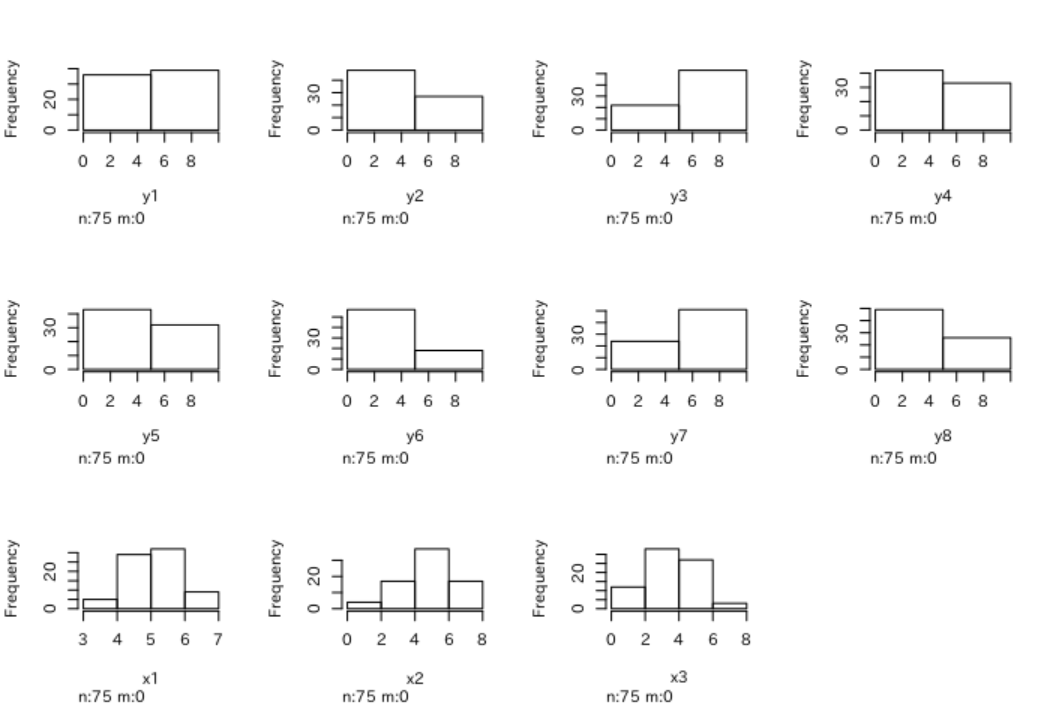
hist(X)
ヒストグラムを見れば、目視でざっくりと正規性を確認できます。
正規分布ではなさそうな変数や、カテゴリ分布の変数などを視覚的に見つけられます。
歪度・尖度
変数ごとの歪度・尖度は次の様に確認できます。正規分布ならどちらも0です。
# 歪度
# 負:左に裾が長い
# 0:左右対称
# 正:右に裾が長い
lapply(X, skew)
# 尖度
# 負:平たい
# 0:正規分布の尖り具合
# 正:尖っている
lapply(X, kurtosis)
分析を実行
fit <- sem(model, data=X)
主なパラメータは次の通りです。
estimator:
meaning : 推定法
options : 色々
default : ML
usage : 基本的に次で良い :
尖度・歪度を調べた結果、
a) 全部の変数に正規性があるなら ML
b) 少し正規性がない変数があるくらいなら MLR
c) それ以外なら WLSMV
ordered:
meaning : カテゴリ変数の列名の配列
usage : カテゴリ変数があるときに設定すれば良い
std.lv:
meaning : モデル識別のための母数制約
options : TRUE (潜在変数の分散・誤差分散を1に固定)
FALSE(潜在変数ごとに、最初のパスの因子負荷量を1に固定)
default : FALSE
std.ov:
meaning : 観測変数を分析前に標準化する
options : TRUE、FALSE
default : FALSE
missing:
meaning : 欠損値の取り扱い
options :
listwise : 欠損を含む行は削除される
fiml : 完全情報最尤推定法が適用される(ml, direct でも可。欠損の仕方が MCAR / MAR の場合のみ有効。)
default : listwise
estimatorは前節の正規性を参考にして選べば良いと思います。ちなみに、上のオススメ推定法3種類の意味は次の通りです。
-
ML:maximum likelihood estimation(最尤推定)です。 -
MLR:MLの亜種です。公式DOCによるとmaximum likelihood estimation with robust (Huber-White) standard errors and a scaled test statistic that is (asymptotically) equal to the Yuan-Bentler test statistic. For both complete and incomplete data.
-
WLSMV:公式DOCにMLMVという、WLSMVのML版の説明があります。maximum likelihood estimation with robust standard errors and a mean- and variance adjusted test statistic (using a scale-shifted approach). For complete data only.
これの
maximum likelihood estimationをdiagonally weighted least squaresに置き換えて読めばOKだと思います。後、このブログも参考になりかもしれません。
orderedはカテゴリ変数があればあるときに設定すればOKだと思います。ちなみに、カテゴリ変数の種類が5値以上で、ヒストグラムがあまり歪んでいない場合は連続変数とみなしても良いかもしれないそうです。(参考:共分散構造分析 R編 7.4 節)
std.lv、std.ovは分析内容に応じて選べば良いと思います。
missingは、適宜使えば良いと思います。
結果を評価
分析結果の概要
summary(fit, standardized=T, fit.measures=T)
主なパラメータは次の通りです。
standardized:
meaning : 標準化推定値も表示
options : TRUE, FALSE
default : FALSE
fit.measures:
meaning : 適合度も表示
options : TRUE, FALSE
default : FALSE
実行すると色々表示されます。省略語の意味(一部)は次の通りです。
<<適合度指標関連>>
[章名]
Model Test User Model : 仮定したモデルの検定
Model Test Baseline Model : 独立モデル(全ての観測変数間にパスを引かず、分散だけ推定するモデル。最悪のモデル)の検定
[項目名]
Test Statistic : 検定統計量(χ2値)
Degrees of freedom : 自由度 = (標本分散の数 + 標本共分散の数) - (母数の数 ( = 係数の数 + 誤差分散の数 ))。
推定するには自由度が1以上ある必要がある。
P-value (Chi-square) : p値。帰無仮説 = モデルが正しい なので有意水準より大きい方が良い。
[列名(評価指標をロバストに算出する推定法(MLRやWLSMV)を使用した場合)]
Standard : 通常通りに算出した場合の値
Robust : ロバストに算出した場合の値
<<推定値関連>>
[章名]
Latent Variables : 測定方程式の推定値
Regressions : 構造方程式の推定値
Covariances : 共分散の推定値
Intercepts : 切片の推定値
Variances : 分散の推定値(外生変数なら分散、内生変数なら誤差分散)
[列名]
Estimate : 推定値
Std.Err : 推定値の標準誤差
z-value : = 推定値/標準誤差。帰無仮説 = 推定値が0 の検定に使用する。
P(>|z|) : 帰無仮説 = 推定値が0 の検定のp値
Std.lv : 潜在変数だけ標準化(平均0・分散1に変換)してから推定した時の推定値
Std.all : 潜在変数と観測変数を標準化してから推定した時の推定値(標準化解と呼ばれる)
-
standardizedとfit.measuresは基本的に True にしておけば良いと思います。(表示が増えるだけなので。) -
標準化解(
std.allの列)では、- パス係数同士を比較できます。「このパスの係数の方があのパスの係数よりも大きいから、この観測変数への影響の方があの観測変数への影響よりも大きいんだな」などと分かります。
- 外生変数同士の共分散が相関係数と一致します。
(参考:共分散構造分析 R編 2.7 節)
適合度
fitMeasures(fit, fit.measures="all")
とりあえずこれを見ておけばOKだと思います。
SRMR
良適合:< 0.05
標本数やモデルの複雑さを考慮していないので、これ単体での判断は望ましくない。
AGFI
良適合:> 0.95
標本数による影響を受けやすい。
RMSEA
良適合:< 0.05
悪適合:> 0.10
rmsea.ci.lower 、 rmsea.ci.upper が90%信頼区間の上限下限。
rmsea.pvalue は帰無仮説を「RMSEA < 0.05」とした時の p値。
CFI・ TLI
良適合:> 0.95
独立モデルのデータへの適合がよい。
つまり、変数間の相関が弱い場合は低めの値になりやすい。
例えば、独立モデルのRMSEA = 0.158 なら、分析モデルのRMSEA = 0.05 でも、TLI < 0.9になってしまうことがある。
なので、この系統の指標だけ適合が悪い時は、独立モデルの適合度を見てみると良い。
AIC・BIC・ECVI
情報量基準系の指標。
値が小さいほどよい。
相対指標なので複数モデルを比較する時に使用する。
AIC、BICはMLなど尤度が出る推定法だけで使用できる。
(参考:共分散構造分析 R編 14章)
ちなみに、自由度 df が小さいと、CFIが良く、RMSEAが悪く、χ2 が悪くなりやすいです。
(参考: 共分散構造分析 疑問編 5.6節)
決定係数
inspect(fit, what="rsquare")
モデル変更の参考に使えるかもしれません。
パス図
semPaths(object=fit, whatLabels="stand")
主なパラメータは次の通りです。
whatLabels:
meaning : 何をパスのラベルにするか。
options : 色々ある
default : パラメータ「what」の値に依存
usage : 例として、stand で標準化解が表示される。
edge.label.cex:
meaning : 係数のフォントサイズ
default : 0.6
sizeMan:
meaning : 観測変数のフォントサイズ
default : 5
sizeLat:
meaning : 潜在変数のフォントサイズ
default : 8
rotation:
meaning : 図の向き
default : 1
nCharNodes:
meaning : 変数名を何文字まで表示するか
default : 3
optimizeLatRes:
meaning : 潜在変数の誤差分散の角度を最適化して表示する。
default : False
実行すると次の様な図がプロットされるはずです。

モデルを改良
修正指標
# 修正指標を計算
MI <- modificationIndices(fit)
# mi昇順で表示
MI[order(MI$mi),]
mi が大きいパスを追加するとモデルが改善するかもしれません。
【 詳しくは 共分散構造分析 R編 4.9節 を参照してください。 】
相関行列(推定値を基に作成)
cor <- inspect(fit, what="cor.all")
heatmap.2(cor, dendrogram='none', Rowv=F, Colv=F)
cor
潜在変数ペアのうち相関係数が高いものは似た様な概念を表しているので、場合によっては一つの潜在変数にしても良いと思います。
相関行列の残差行列
cor <- resid(fit, type="cor")
cor <- cor$cov
heatmap.2(cor, dendrogram='none', Rowv=F, Colv=F)
cor
絶対値が大きい要素がある変数に集中していれば、その変数を削除したりその変数へのパスを変更するなどすると良いかもしれません。
相関行列(観測データを基に作成)
cor.plot(X)
以下の様な事柄について考察できます。
変数間の関連性
列同士(または行同士)のグラデーションが似ている変数同士は何かしらの関連性を有している可能性が高いです。例えば、
- 片方の変数が他方の変数に大きく影響している
- 各変数の背後に共通の潜在変数が存在する
などが想定されます。
多重共線性の有無
共分散構造分析が上手くいかない時に、このヒートマップを参考にして多重共線性を持つ変数群を発見できるかもしれません。(回帰式の説明変数間に多重共線性があると、共分散構造分析が上手くいかない場合があります。)
モデル作成のヒント
典型的なモデルの種類
共分散構造分析 R編に掲載されているモデルの種類の内、色々な場面で使われていそうだと思ったものをまとめました。詳しくは共分散構造分析 R編を参照してください。
多次因子分析モデル
潜在変数→潜在変数 という構造を含むモデルのことです。
モデル例(2次因子分析の場合):
# 1次因子
f1 =~ x1 + x2 + x3
f2 =~ x4 + x5 + x6
f3 =~ x7 + x8 + x9
# 2次因子
f4 =~ f1 + f2 + f3
因子の背後に新たな因子を導入するケースの例:
- 因子間に強い相関が見られる時など
因子と観測変数の間に新たな因子(中間因子と呼ばれる)を導入するケースの例:
- 多重共線性の解消
- 1因子で適合度が低い時、その下に複数の中間因子を入れると適合度が上がる場合がある
- 複数回の測定において、独自因子を特殊因子(構成概念以外によるものの影響)と測定誤差に分ける場合
【 詳しくは 共分散構造分析 疑問編 7.2節を参照してください。 】
【 詳しくは 共分散構造分析 R編 3.5節 を参照してください。 】
階層因子分析モデル
一部の観測変数に影響を与えるグループ因子と、全ての観測変数に影響を与える一般因子の2種類を仮定するモデル。グループ因子と一般因子の間には相関がないと仮定する事が特徴。
モデル例:
# グループ因子
f1 =~ x1 + x2 + x3
f2 =~ x4 + x5 + x6
f3 =~ x7 + x8 + x9
# 一般因子
F =~ x1 + x2 + x3 + x4 + ... + x9
# グループ因子と一般因子の間には相関がないと仮定
F ~~ 0*f1 + 0*f2 + 0*f3
2因子分析モデルとの比較:
- 階層因子分析モデルでは、グループ因子と一般因子が独立という仮定があるので、その様な仮定のない2因子分析モデルの方が解釈はしやすい。
- 階層因子分析モデルの方が適合度が良くなりやすいが、それは母数が多いから。
【 詳しくは 共分散構造分析 R編 3.5節 を参照してください。 】
MIMICモデル
Multiple Indicator MultIple Cause Model の略です。観測変数→潜在変数→観測変数 という構造のモデルのことです。
モデル例:
f ~ x1 + x2 + x3
f =~ x4 + x5 + x6
潜在変数には誤差を仮定する場合もしない場合もあります。
【 詳しくは 共分散構造分析 R編 3.4節 を参照してください。 】
PLSモデル
Partial Least Squares Model の略です。観測変数→潜在変数(誤差分散0と仮定)→潜在変数→観測変数 という構造のモデルのことです。一つ目の潜在変数の誤差分散を0に固定する事で、観測変数の加重和になるようにしています。
モデル例:
f1 ~ x1 + x2 + x3
f2 =~ x4 + x5 + x6
f1 =~ f2
f1 ~~ 0*f1 # 誤差分散 == 0 だと仮定
f2 ~~ f2 # 誤差の存在を仮定
【 詳しくは 共分散構造分析 R編 3.4節 を参照してください。 】
共分散構造分析の特殊なパターン
平均共分散構造分析
潜在変数の平均を推定できます。ユースケースの例は次の通りです。
- 複数の母集団を比較
- 男性データ vs 女性データ で比較
- 去年データ vs 今年データ で比較
- 潜在変数同士を比較
【 詳しくは 共分散構造分析 R編 第5章を参照してください。 】
多母集団同時分析
母集団同士で因子の切片を比較できます。多母集団同時分析をする事で、母集団間で因子の意味が異なってしまう可能性をなくせます。
【 詳しくは 共分散構造分析 R編 第6章を参照してください。 】
双方向パス
双方向パスとは、 x1 ⇆ x2 という様に相互にパスを出し合っている構造のことです。双方向パスがある場合、片方の変数にだけパスを出している第3の変数(道具的変数と言います)が必要です。例えば、x1 ⇆ x2 ← x3 というパス図なら、x3が道具的変数です。
【 詳しくは 共分散構造分析 R編 p.49を参照してください。 】
共変関係
共変関係を仮定するケース
変数群に共通の変動要因が仮定されるが、観測変数や潜在変数に加えたくない、という場合に導入します。
例えば、
- 測定内容は同じだが測定時期が異なる場合。例えば、PoliticalDemocracy の「y1 ~ y4」と「y5 ~ y8」の関係性など。
- 体力測定で、他人に見られながら測定した項目同士(50m走など)と、そうでない項目同士(腕立て伏せなど)
また、3以上の観測変数に大きな誤差間相関がある場合は、背後に因子がある可能性があります。新しい因子の導入を検討しても良いと思います。
(参考: 共分散構造分析 疑問編 1.12節)
また、sem()では「外生変数の観測変数間」と「外生変数の潜在変数間」には自動で共変関係が付きます。sem()の代わりにlavaan()を使用すれば自動で付かなくなりますが、いくつかのパラメータのデフォルト値も変わります。
母数への条件付け
共分散構造分析 R編 3.8節、4.7節を参考にしました。
母数間の等値制約
ケース例:測定内容は同じだが測定時期が異なる変数ペアがある場合。誤差の原因は同じはずなので、それらの誤差分散に等値制約を設けます。
# 誤差の原因は同じはずなので、誤差分散に等値制約を設ける
x1 ~~ c*x1
x2 ~~ c*x2
# 併せて、共変関係を仮定する場合も多いです。(測定内容は同じなので。)
x1 ~~ x2
母数の固定
ケース例:sem()のパラメータのstd.lvをFALSEにした場合に、係数を1に固定するパスを最初のパス以外にする場合
# x1 ではなく x2 の係数を1に固定する
f1 =~ NA*x1 + 1*x2 + x3
母数の不等式制約
ケース例:ヘイウッドケース(推定結果に負の分散が生じてしまう事)を回避する場合
# x の分散が負にならないようにする
x ~~ a*x; a>0
母数間の関係を制約
条件に応じて設けると良いと思います。
# 例1
y ~ b1*x1 + b2*x2 + b3*x3
b1 == (b2 + b3)^2
# 例2
y ~ a*x1 + b*x2
a > b
# 例3
y ~ b1*x1 + b2*x2 + b3*x3
b1 > exp(b2 + b3)
直接効果・間接効果・総合効果
x1 ---------> x3
|----- x2 ----↑
というパス図で x1 が x3 に与える効果は、
-
直接効果 :
x1 → x3のルート -
間接効果 :
x1 → x2 → x3のルート -
総合効果 : 直接効果 + 間接効果
式にすると、
x1 ~ a*x3
x2 ~ b*x3
x1 ~ c*x2
# 間接効果
bc := b*c
# 総合効果
total := a + (b*c)
この様に bc や total を定義しておくと、summary()でその値を表示してくれます。
(参考:共分散構造分析 R編 4.8節)
sem()のヒント
std.lv の設定
TRUEにすると、潜在変数の分散・誤差分散が1に固定されます。
FALSEにすると、潜在変数ごとに最初のパスの係数が1に固定されます。
基本的に、係数の値が大事ならTRUE、分散の値が大事ならFALSEで良いと思います。
※ただし、TRUEにした時、条件によっては一部の潜在変数だけが固定されるそうです。パッケージのDOCにはこう書いてあります:
std.lv: If TRUE, the metric of each latent variable is determined by fixing their (residual) variances
to 1.0. If FALSE, the metric of each latent variable is determined by fixing the factor loading
of the first indicator to 1.0. If there are multiple groups, std.lv = TRUE and "loadings" is
included in the group.label argument, then only the latent variances i of the first group will
be fixed to 1.0, while the latent variances of other groups are set free.
sem()のgroup.labelのデフォルト値はよく分からないです…。
また、TRUEとFALSEで、
- 標準化解は同じです。(異なる場合は、収束していなかったりする可能性があります。)
- 非標準化解は異なります。
また、分散やパス係数の固定値を1以外にした場合も、
- 標準化解は同じです。
- 非標準化解は異なります。
WARNINGの対処
共分散構造分析 疑問編 3.8 ~ 3.12節、共分散構造分析 数理編 11章を参考にしました。
WARNINGの種類
標本分散の桁が変数間で大きく異なる
lavaan WARNING: some observed variances are (at least) a factor 1000 times larger than others; use varTable(fit) to investigate
この場合、標準化解は問題ありませんが、非標準化解はたまに問題が出る場合があります。桁が大きな変数を10で割っておくなどすると良いかもしれません。(10で割ると分散は 1 / 100 倍になります。)
参考:https://groups.google.com/g/lavaan/c/ybSDdk0pdno?pli=1 の以下の文章
Surprising things happen in SEM when observed variables differ substantially in scale. the warning is giving you good advice. You can easily rescale by, for example, dividing your larger-scale variables by some power of 10. Diving the variable by 10 divides its variance by 100.
ヘイウッドケース(誤差分散の推定値が負の変数がある)
lavaan WARNING: some estimated ov variances are negative
lavaan WARNING: some estimated lv variances are negative
上なら観測変数(observed variable、ov)、下なら潜在変数(latent variable、lv)の誤差分散が負になっています。
原因の候補はこの後紹介しますが、とりあえず対処したい場合は次の方法があります。
- 非負値制約を付ける(
x ~~ a*x; a>0)。適合度が良く、あまり負に大きく無い場合に行う。負に大きい場合はモデルがデータに適合していない可能性が高いので、モデルを変更した方が良い。 - 誤差分散を 0 に固定する(
x ~~ 0*x)。 - 推定法を変える。
- 負の誤差分散になる変数を除外する。
情報行列の逆行列が求まらない( = 正定値でない)
lavaan WARNING: Could not compute standard errors! The information matrix could not be inverted. This may be a symptom that the model is not identified.
潜在変数の共分散行列が正定値でない
lavaan WARNING: covariance matrix of latent variables is not positive definite;
use inspect(fit,”cov.lv”) to investigate.
潜在変数間に1を超える相関を持つペアがある場合に起こります。エラーメッセージではinspect(fit,”cov.lv”)を提案していますが、これだと共分散が表示されるので、inspect(fit,”cor.lv”)で相関係数を見た方が良いです。どの潜在変数ペアの相関に問題があるのかを参考にして、モデルを変えると良いと思います。(参考:https://clover.fcg.world/2016/05/24/4903)
収束しない
lavaan WARNING: model has NOT converged!
標準化解の絶対値が1を超えている
WARNING は表示されず、summary()などで確認すると分かります。
標準化解はパス係数も分散(誤差分散)も通常は絶対値が1以下になります。1を超えているのであれば、何かしら問題のあるモデルの可能性が高いです。
ただし、例外もあります。単方向パスで値が1.01の様に少し超える程度の場合は、モデルは正当な事もあるそうです。(ちなみに、双方向パスの場合はパス係数が相関係数に等しいので1を超えていたら不適解とみなせます。)
原因の候補(いくつかは対処法も併記)
種類の「標本分散の桁が変数間で大きく異なる」以外についてです。
-
標本
- 観測変数の標本変動
- 外れ値
- サンプルサイズが小さい
- (ヘイウッドケースで)母共分散が0に近い
-
モデル全般
-
単純に当てはまりが悪い
-
母数が多い
-
モデルが複雑
【対処法】 複雑だが正しい場合、初期値を変えると上手くいくことがあります。
-
-
潜在変数
-
過度な因子化
-
出ていくパスの数が2つ以下
【対処法】「母数に制約をつける」「他の因子とパスをつなぐ」などで測定可能になりますが、安定しない事もあります。
-
-
観測変数間の関係
-
多重共線性(相関係数0.95以上の観測変数ペアがあるなど)
【対処法】
a) 片方を除外する。
b) 両方とも組み込んだ方が妥当そうな場合、誤差分散を0に固定してしまう。
c) 中間因子を導入する:
v2 --> v1 v3 ----↑ という構造で、v2とv3の相関係数が大きく、それぞれのパス係数が大きく異なる(正負が逆など)場合、多重共線性がある可能性がある。そこで中間因子 f を導入する。 v2 -> f -> v1 v3 ---↑ -
変数間に非線形な関係がある
【対処法】散布図を描いて非線形の関係があれば、変数変換をして解消できるかもしれません。
-
-
誤差変数
-
強い相関がある誤差変数ペアがある
【対処法】共変関係を付けるか、背後に新しい因子を仮定すれば解消する事があります。
-
(ヘイウッドケースで)因子に大きな影響を受けている観測変数において、誤差分散がとても小さくなり負になる(モデルが正しくても起こる)
-
-
パス係数
- (ヘイウッドケースで)パス係数の真値がとても小さい
- パス係数が大きなパスが少ない
その他
引っかかりやすい点
- ある変数の「分散」と「誤差分散」は別物です。
実際に分析する際のコードの例
model.txtを編集しつつ実行用コード.Rを実行してモデルの改良具合を見るスタイルです。参考にどうぞ。
実行用コード.R
# データを読み込む
X <- read.csv('data.csv')
# モデルが書かれたファイルを読み込む
# モデルを別のファイルに書いておく事で、
# モデルごとに実行用コードをコピペしたりする手間が省ける
filename <- 'model.txt'
lineAry <- readLines(filename)
model <- paste(lineAry, collapse='\n')
# sem実行
fit <- sem(model, data=X, estimator="WLSMV", std.lv=T, std.ov=T)
# 主要な適合度を表示
# これを見て「モデルがちょっと良くなったぞ」「急に悪くなったな」などと言いながらモデルを改良していく
fitMeasures(fit, fit.measures=c('rmsea.scaled', 'cfi.scaled', 'tli.scaled', 'agfi', 'srmr'))
# 推定値を表示
# fitMeasuresの適合度だけでなくsummaryで推定値を見ることも多い
summary(fit, standardized=T, fit.measures=T)
# 推定値の絶対値が1超の箇所を表示
# もしあれば推定が上手くいっていない可能性がある
# また、モデル改変の参考にできる事もある
p <- parameterEstimates(fit, standardized=T)
p[p$std.all > 1,]
p[p$std.all < -1,]
# 適合度を全て表示
# 気になる場合に見たりする
fitMeasures(fit, fit.measures="all")
# 潜在変数スコアを保存
# 実験結果の考察などのために保存する
factor_score <- lavPredict(object=fit, append.data=T)
write.csv(factor_score, "factor_score.csv")
model.txt
# 測定方程式
ind60 =~ x1 + x2 + x3
dem60 =~ y1 + y2 + y3 + y4
dem65 =~ y5 + y6 + y7 + y8
# 構造方程式
dem60 ~ ind60
dem65 ~ ind60 + dem60
# 共変関係
y1 ~~ y5
y2 ~~ y4 + y6
y3 ~~ y7
y4 ~~ y8
y6 ~~ y8
付録:探索的因子分析
はじめに
共分散構造分析では、潜在変数を仮定した上で分析を行います。とはいえ、最初はどの様な潜在変数を仮定すれば良いのか、検討がパッと付かない場合もあります。
その様な場合に役立つかもしれない手法が探索的因子分析(Exploratory factor analysis、EFA)です。探索的因子分析では、いくつかの潜在変数があるという前提の下、潜在変数の数を仮定し、それらの潜在変数から各観測変数への影響の度合いを推定します。推定した結果は、データへの当てはまりの良さを表す指標を使って評価できます。そこで、潜在変数の数を変化させて、当てはまりが良い場合の結果を利用して、共分散構造分析の潜在変数を仮定する、という訳です。
なお、探索的因子分析では、潜在変数の事を単に「因子」と呼ぶ事もあります。本記事では因子と呼ぶ事にします。
探索的因子分析の基本的なやり方は 共分散構造分析 R編 1.7 ~ 1.9節に記載されています。
実際にやってみる
因子数の見当をつける
有用なライブラリがあるので、それを利用します。(参考:Rで因子分析 商用ソフトで実行できない因子分析のあれこれ)
VSS(Very Simple Structure)
VSSは、因子数を変えた時の各種評価指標の値と、最適と思われる因子数を表示してくれます。評価指標は、MAP、BIC の提案数を見ると良いです。
VSS(X, rotate='oblimin')
主なパラメータは以下の通りです。適宜変更してみてください。
n:
meaning : 因子の最大候補数
default : 8
rotate:
meaning : 回転方法
options : none, varimax, oblimin, promax (斜交回転は promax と oblimin)
default : varimax
usage : 基本的に oblimin で良い
fm:
meaning : 推定法
options : pa, minres, mle, fa( mle は ml でも可)
default : minres
usage : 基本的に minres、サンプルサイズが大きければ ml で良い
実行すると次の様な出力が表示されるはずです。
Very Simple Structure
Call: vss(x = x, n = n, rotate = rotate, diagonal = diagonal, fm = fm,
n.obs = n.obs, plot = plot, title = title, use = use, cor = cor)
VSS complexity 1 achieves a maximimum of 0.89 with 1 factors
VSS complexity 2 achieves a maximimum of 0.84 with 2 factors
The Velicer MAP achieves a minimum of 0.05 with 2 factors
BIC achieves a minimum of NA with 2 factors
Sample Size adjusted BIC achieves a minimum of NA with 5 factors
Statistics by number of factors
vss1 vss2 map dof chisq prob sqresid fit RMSEA BIC SABIC complex eChisq SRMR eCRMS eBIC
1 0.89 0.00 0.096 44 2.4e+02 2.2e-28 4.9 0.89 0.242 48 186.37 1.0 1.8e+02 1.5e-01 0.164 -12
2 0.81 0.84 0.046 34 5.7e+01 7.9e-03 7.2 0.84 0.094 -90 17.44 1.0 1.5e+01 4.3e-02 0.054 -132
3 0.50 0.67 0.054 25 3.0e+01 2.4e-01 12.8 0.72 0.048 -78 0.44 1.3 4.2e+00 2.2e-02 0.033 -104
4 0.46 0.56 0.076 17 1.7e+01 4.2e-01 16.8 0.63 0.014 -56 -2.34 1.3 2.4e+00 1.7e-02 0.031 -71
5 0.34 0.47 0.100 10 9.1e+00 5.2e-01 19.2 0.57 0.000 -34 -2.58 1.6 8.7e-01 1.0e-02 0.024 -42
6 0.36 0.44 0.145 4 4.4e+00 3.5e-01 20.5 0.55 0.034 -13 -0.26 1.6 2.9e-01 6.0e-03 0.022 -17
7 0.35 0.42 0.216 -1 9.1e-01 NA 22.9 0.49 NA NA NA 1.5 4.8e-02 2.4e-03 NA NA
8 0.32 0.41 0.345 -5 3.7e-07 NA 20.4 0.55 NA NA NA 1.6 2.1e-08 1.6e-06 NA NA
警告メッセージ:
GPFoblq(L, Tmat = Tmat, normalize = normalize, eps = eps, maxit = maxit, で:
convergence not obtained in GPFoblq. 1000 iterations used.
警告メッセージが出ていますが、説明上問題ないので無視します。
提案数は次の通りです。
- MAP:2因子(
The Velicer MAP achieves a minimum of 0.05 with 2 factors) - BIC:2因子(
BIC achieves a minimum of NA with 2 factors)
平行分析
平行分析 fa.parallel では、探索的因子分析での提案数(number of factors)と主成分分析での提案数(number of components)が表示されます。
fa.parallel(X)
主なパラメータは次の通りです。
fm:
meaning : 推定法
options : minres, ml, uls, wls, gls, pa
default : minres
usage : 基本的に minres、サンプルサイズが大きければ ml で良い
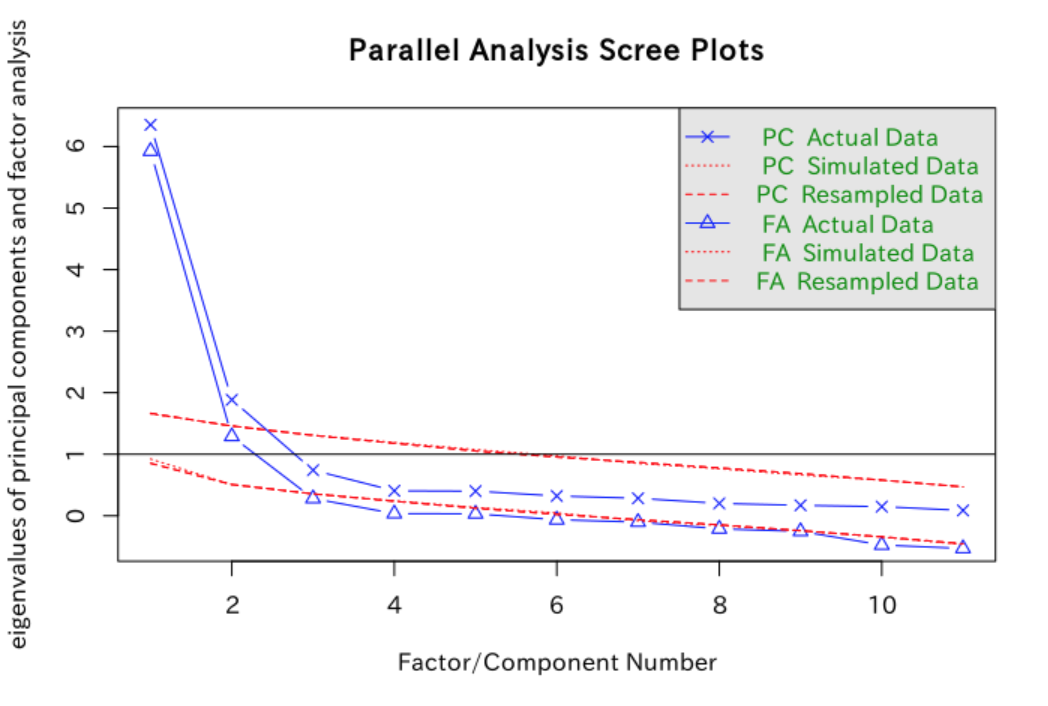
実行すると次の様な画像がプロットされるはずです。
また、次の様な出力が表示されるはずです。
Parallel analysis suggests that the number of factors = 2 and the number of components = 2
探索的因子分析と主成分分析の両方で2因子が提案されています。
見当をつけた因子数における分析結果を表示する
前節の結果、2因子が良さそうだと分かりました。
そこで、2因子の場合の結果の詳細を調べます。
まずは次の様に探索的因子分析を実行します。
Xfa_rotate <- fa(X, nfactors=2)
主なパラメータは次の通りです。
nfactors:
meaning : 因子数
usage : 見当を付けた因子数を試せば良い
rotate
meaning : 斜交回転の方法
options : 色々ある
default : oblimin
usage : 基本的に oblimin で良い
fm
meaning : 推定法
options : 色々ある
default : minres
usage : 基本的に minres、サンプルサイズが大きければ ml で良い
次に、結果の詳細を表示します。
Xfa_rotate
次の様に出力されるはずです。
Factor Analysis using method = minres
Call: fa(r = X, nfactors = 2)
Standardized loadings (pattern matrix) based upon correlation matrix
MR1 MR2 h2 u2 com
y1 0.88 -0.07 0.72 0.277 1.0
y2 0.83 -0.15 0.59 0.411 1.1
y3 0.70 -0.01 0.48 0.523 1.0
y4 0.83 0.07 0.74 0.257 1.0
y5 0.68 0.22 0.66 0.344 1.2
y6 0.79 -0.01 0.62 0.385 1.0
y7 0.80 0.03 0.67 0.327 1.0
y8 0.80 0.09 0.70 0.295 1.0
x1 0.05 0.91 0.87 0.133 1.0
x2 0.00 0.97 0.94 0.059 1.0
x3 -0.03 0.88 0.75 0.249 1.0
MR1 MR2
SS loadings 5.06 2.68
Proportion Var 0.46 0.24
Cumulative Var 0.46 0.70
Proportion Explained 0.65 0.35
Cumulative Proportion 0.65 1.00
With factor correlations of
MR1 MR2
MR1 1.00 0.47
MR2 0.47 1.00
Mean item complexity = 1
Test of the hypothesis that 2 factors are sufficient.
The degrees of freedom for the null model are 55 and the objective function was 9.74 with Chi Square of 677.07
The degrees of freedom for the model are 34 and the objective function was 0.84
The root mean square of the residuals (RMSR) is 0.04
The df corrected root mean square of the residuals is 0.05
The harmonic number of observations is 75 with the empirical chi square 14.95 with prob < 1
The total number of observations was 75 with Likelihood Chi Square = 57.07 with prob < 0.0079
Tucker Lewis Index of factoring reliability = 0.939
RMSEA index = 0.094 and the 90 % confidence intervals are 0.049 0.138
BIC = -89.72
Fit based upon off diagonal values = 0.99
Measures of factor score adequacy
MR1 MR2
Correlation of (regression) scores with factors 0.97 0.98
Multiple R square of scores with factors 0.94 0.96
Minimum correlation of possible factor scores 0.88 0.93
表示内容を読み取っていきます。
まず、一番上にあるStandardized loadingsを見ます。値の意味は次の通りです。
| 列名 | 表しているもの | 意味 |
|---|---|---|
| MR1、MR2 | 因子負荷 | 潜在変数から各観測変数への影響の度合いを表します。 |
| h2 | 共通性 | 共通因子(潜在変数)による説明の割合です。 |
| u2 | 独自性 | 独自因子(誤差変数)による説明の割合です。u2 = 1 - h2 の関係があります。 |
| com | 複雑性 | 単純構造の指標です。 1つの因子だけから影響を受けていると1になり、全部の因子からで因子数になります。 |
MR1とMR2の値を見ると、y1 ~ y8 は MR1 からの影響が大きく、x1 ~ x3 は MR2 からの影響が大きい事が分かります。
また、全般的にcomが1に近く、どの観測変数も概ね単一の因子から影響を受けている事が分かります。
次に、その下の表を見ます。値の意味は次の通りです。
| 行名 | 表しているもの | 意味 |
|---|---|---|
| SS loadings | 寄与 | 全ての観測変数にどのくらい影響を与えているかを意味する。 |
| proportion var | 寄与率 | 寄与率 = 寄与 / 観測変数の総数 |
| cumulative var | 累積寄与率 | 寄与率の累積値 |
| proportion explained | 説明率 | 説明率 = 寄与 / 寄与の和 |
| cumulative proportoin | 累積説明率 | 説明率の累積値 |
これらの値も分析で参考になるかもしれません。
(以上用語参考:因子分析のp.6、160201Rによる因子分析のp.4、因子分析とは|市場調査ならインテージの「因子負荷量の抽出結果の見方」、共分散構造分析 R編 1.8節)
さて、共分散構造分析のモデルを作成するにあたって、因子負荷の絶対値が大きなものをパスとして仮定する、という方法があります。以下で絶対値が大きな因子負荷だけを表示できます。
Xfa_rotate$loadings
出力:
Loadings:
MR1 MR2
y1 0.881
y2 0.827 -0.151
y3 0.697
y4 0.827
y5 0.682 0.220
y6 0.790
y7 0.804
y8 0.796
x1 0.907
x2 0.968
x3 0.880
MR1 MR2
SS loadings 5.005 2.624
Proportion Var 0.455 0.239
Cumulative Var 0.455 0.693
この出力から、共分散構造分析のモデルとして、
-
y1~y8に影響する潜在変数 -
x1~x3とy2、y5に影響する潜在変数
の2つを仮定すると良いかもしれない事が分かります。ただし、実際に仮定する時は、あくまで参考としてこの結果を利用すると良いと思います。観測変数の意味や、既存のその他の知見に基づいて、柔軟にモデルを組むと良いはずです。