はじめに
「え!?好きなタイプですか?うーん...まっすぐな人かな...。」
そんな直線系男子がお好みな貴女、お待たせしました、まっすぐな人はすぐには見つけられませんが、まっすぐなものなら画像からすぐに抽出できます。
ということで、本記事では、画像から直線を検出するスタンダードな手法であるHough変換について解説したいと思います。
なぜ今更こんなベーシックな技術を解説するかというと、
- それがdual spaceでの検出である、という解釈が見当たらなかった
- 改良方法についての解説が少ない
- 変換、と呼ばれる所以についての解説が見当たらなかった
- OpenCVで投票値、もしくは投票順位順に取る方法が見当たらなかった
からです。
Hough変換とは
dual spaceで、投票によりprimitive(e.g. 直線、円)を見つける手法です。
(以下に上記意味の解説を述べます。)
Hough変換による直線検出のアルゴリズム解説
1. dual spaceの導入
見つけたい直線を、
$$ax+by+c=0$$
と表します。cが0でなければ式全体をcで割ることにより、c=1として一般性を失いません。cが0の場合は後ほど扱います。
ここで、homogeneous coordinateを導入します。
$\boldsymbol{l}=(1,a,b)^T, \boldsymbol{x}=(1,x,y)^T$と置けば、上式は、
$$\boldsymbol{l}^T \boldsymbol{x} = 0$$
と表されます。これを図で表したものが下図です。
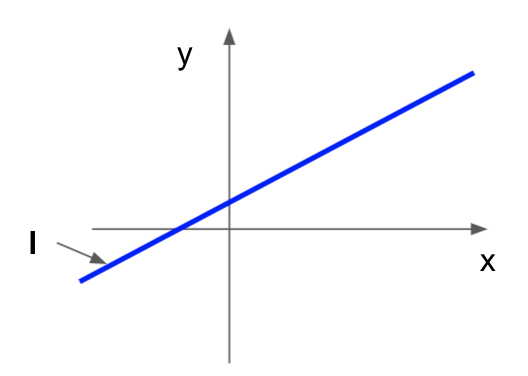
lを固定した時、$\boldsymbol{l}^T \boldsymbol{x} = 0$を満たすxは、上図の青い線上の全てを動きます。つまり、lが直線を表していると言えます。
さて、内積は順序によらないので、これを
$$\boldsymbol{x}^T \boldsymbol{l} = 0$$
と書いてみましょう。先程のlとxの役割が入れ替わっています。これを係数の空間で描くと、一つの係数lは、一点に対応するので、下図のようになります。
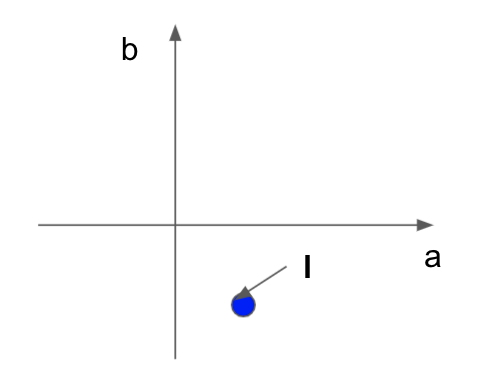
元の空間での直線lが、係数の空間では点となるのです。この係数の空間をdual spaceと呼びます。(数学的には、xに作用するlの空間であるからdual spaceと呼ばれ、テンソル表記で$\boldsymbol{x}$は、$x^{\mu}$であり、dual spaceの元$\boldsymbol{l}$は$l_{\mu}$と書かれます。)
点と直線の関係は、完全に入れ替えることができ、それぞれの空間での役割は入れ替わります。即ち、元の空間の直線は、係数の空間の点となり、完全にx,lの見方を入れ替えることにより、係数の空間の直線は、元の空間の点になります。これを図で表してものが下図です。
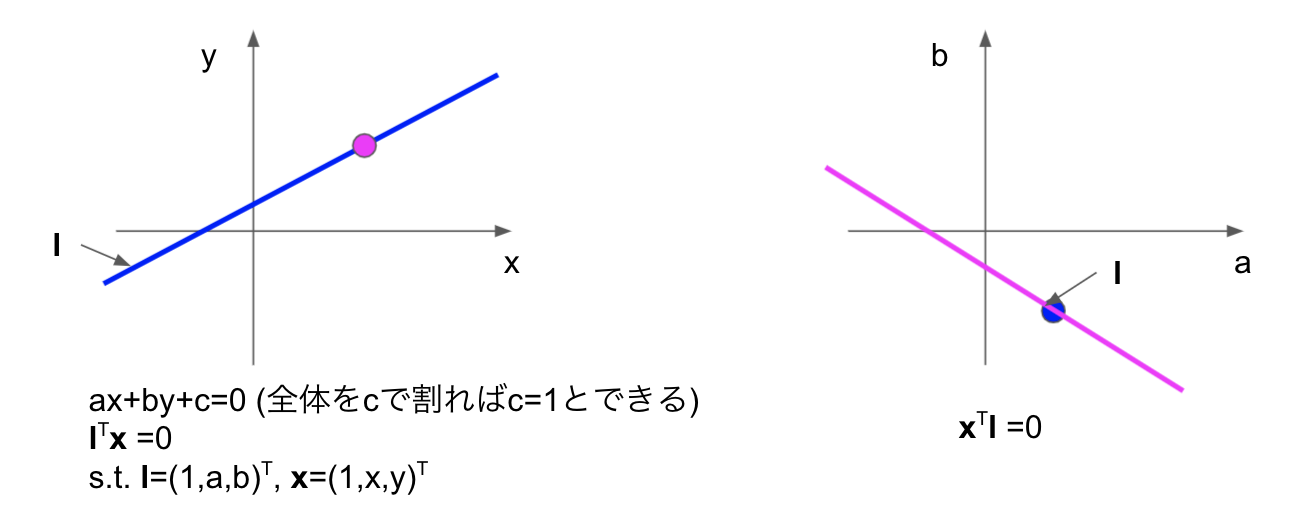
ref: wikipedia dual space
ref: "Multiple View Geometry in computer vision" R.Hartley and A.Zisserman, p.29 Duality.
2. 元々のHough変換による直線検出
さて、ではどうやって直線を見つけるか、をお話しましょう。
元画像に対し、cannyなどのエッジ検出をかけてエッジ点を抽出します(この時点でエッジ画像は2値画像です)。抽出された全てのエッジ点を、順番にピックアップし(上図でのピンクの点)、dual spaceに直線としてplotします。2つ目の点を抽出したのが下図です。
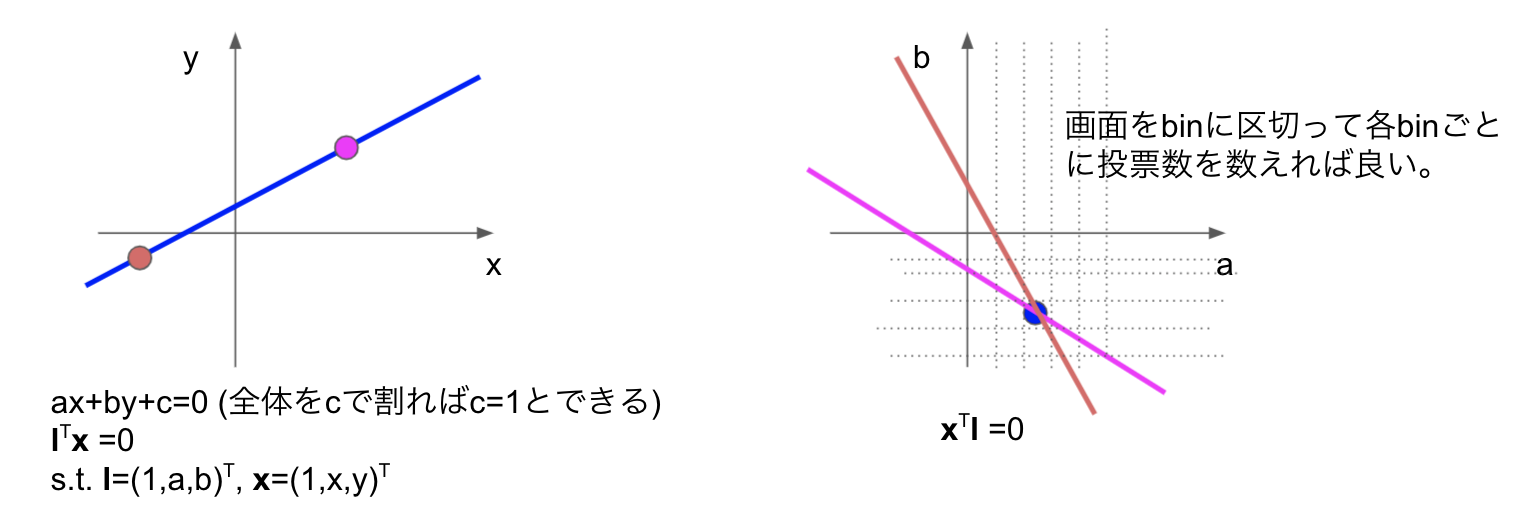
こうして全エッジ点に対して操作を行うと、dual spaceにエッジ点と同じ数だけの直線が描かれ、dual spaceの画面をbinに区切って、各binごとに投票数を数えます。この投票数が多いところが、直線らしいパラメータlであり、投票数が直線らしさを表すスコアになっています。
これがHough変換の原理です。
3. 元のHough変換の課題
Houghというのは本アルゴリズムの発明者の名前で、元々のHough変換は前節のものでした。
しかし、現在用いられているのは、次節で紹介する、Duda & Hartが一般化した一般化Hough変換です。
前節のHough変換の何が問題かというと、$c\neq0$を仮定したことでした。これでは、c=0の原点を通る直線が表せません。では、aやbで割ってはどうか、と思うかもしれませんが、同様にa=0,b=0の場合を扱えません。
ちなみに、なぜa,b,cのまま3つのパラメータで表現していてはだめで、何かで割る必要があるかというと、元々2次元画像中での直線の自由度は2なので、dual spaceは独立なパラメータの数の2次元で表す必要があるからです。
これを解決する手法が、以下で説明する一般化Hough変換です。
ref: wikipedia hough transform
4. 一般化Hough変換
まず、はじめから2つのパラメータのみを用いた、直線のパラメータ表示を定義します。
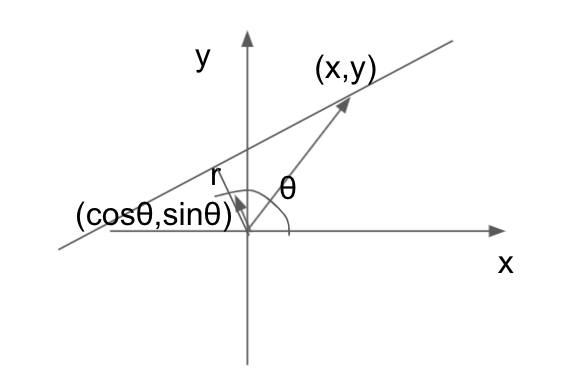
下図で、直線上の任意の(x,y)ベクトルと、$(\cos\theta, \sin\theta)$ベクトルの内積を考えると、(x,y)の$(\cos\theta, \sin\theta)$上への射影となるため、いつも原点から直線までの距離rになります。
すなわち、
$$x \cos\theta + y \sin\theta = r$$
となります。これが直線のパラメータ表示です。
さて、ここで、$\boldsymbol{l}=(-r,\cos\theta, \sin\theta)^T, \boldsymbol{x}=(1,x,y)^T$とおけば、再び
$$\boldsymbol{l}^T \boldsymbol{x} = 0$$
となります。このときの独立なパラメータはr,$\theta$です。
ここで、$r-\theta$を軸としたdual spaceを考えると、間にarcsinの非線形関数が入るので、今度は、点xは、(合成関数を使うことにより、sine curveの)曲線となります。逆に、$r-\theta$ dual spaceの点は、元の空間の直線になります。これを図で表したものが下図です。
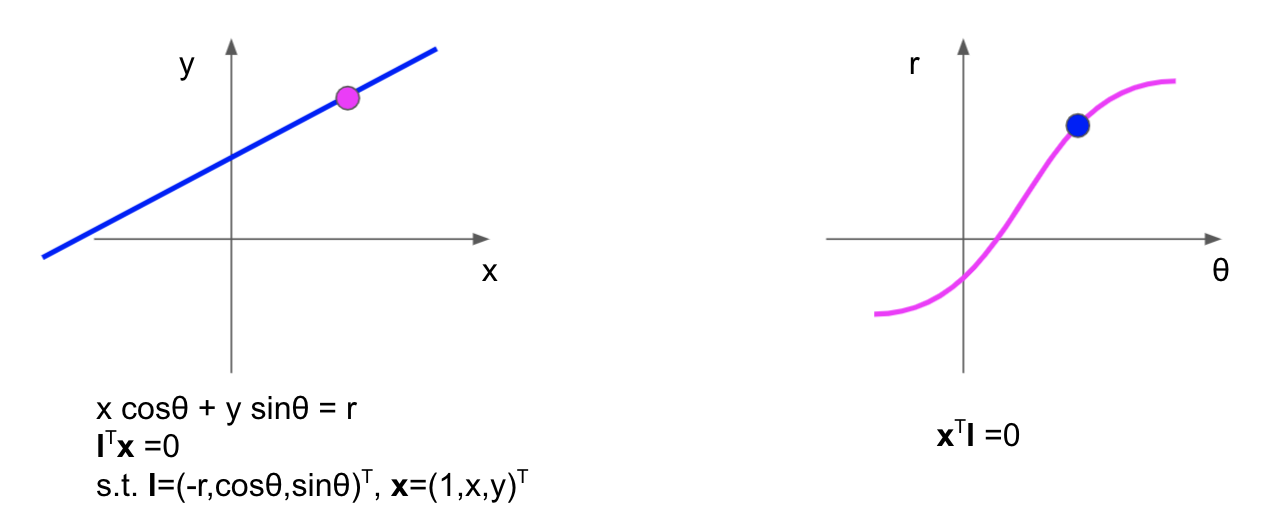
実際に直線検出する場合は、前回同様に、複数のエッジ点をdual spaceに下図のように投票して、投票値をしきい値で抜き出せば、元の空間での直線が検出できます。
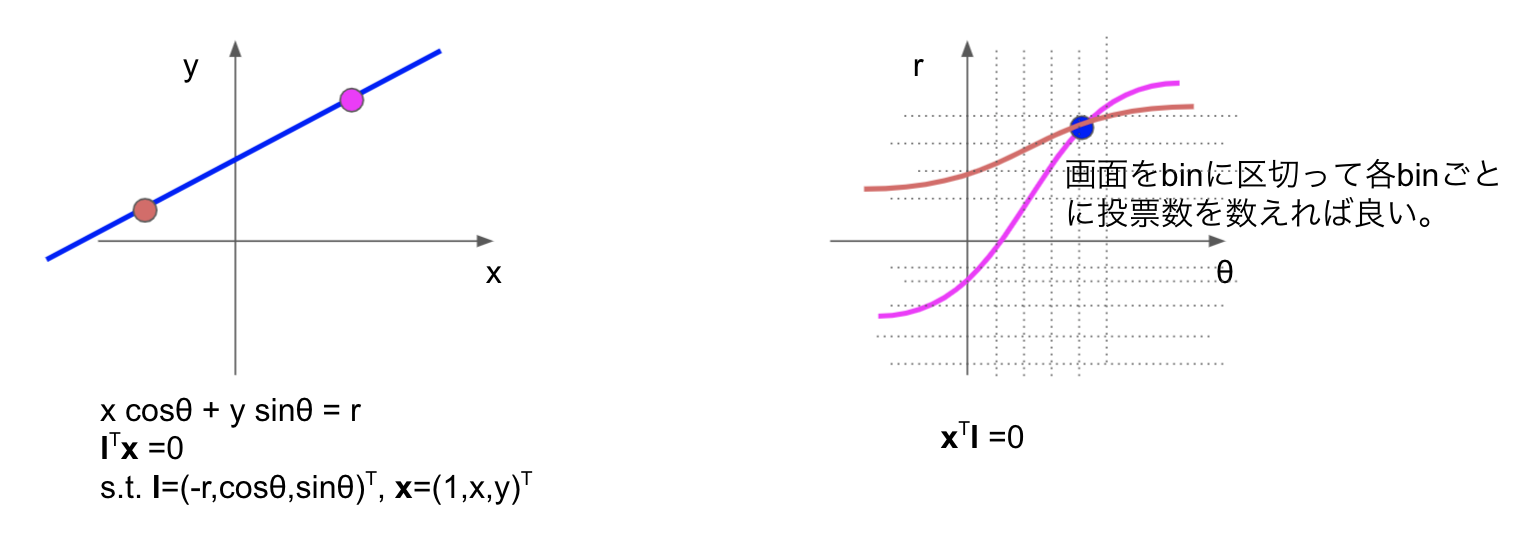
Hough変換による円検出のアルゴリズム解説
単純に、以下の円の式
$$(x-a)^2 + (y-b)^2 = r^2$$
において、独立なパラメータ(a,b,r)を軸とするdual spaceに投票するだけで、後は直線検出の場合と同じです。3次元空間(a,b,r)への投票となる分、パラメータ空間は大きくなります。
変換と呼ばれる所以
フーリエ変換が、任意の関数を、無限個の基底の線形結合で表した空間への写像であったことを思い出すと、Hough変換も、パラメータ空間への写像をしていることから、「変換」という名前がついたことは理解できます。ただ、Hough変換自体は、変換後の空間(dual space)で投票を行って、その投票値に基づいて、直線や円を検出する手法なので、"Hough変換とは" のところで述べたように、
「dual spaceで、投票によりprimitive(e.g. 直線、円)を見つける手法。」
と言えるのです。
Hough変換の派生
- weighted Hough: 先程は2値化したエッジ画像を入力として用いましたが、エッジ検出の値を2値化せずそのまま使い、投票値に重み付けをする
- probabilistic Hough: 全エッジ点ではなく、ランダムに(確率的に)点を抽出することにより、計算時間を削減した方法。
他の直線検出手法との比較
- 直線らしさで順位付けされた直線が、任意本抽出できる。
- 最も一般的な直線検出の手法として、最小二乗法がある。しかし、最小二乗法は、基本的には全部の点を、ノイズを含んだ、1つの直線上の点として考え、最も確からしい直線を引く方法であるので、複数の直線を見つけるには別な工夫がいる。
OpenCVでHough変換の投票上位順に抽出する方法
OpenCVでのHough変換の実装cv::HoughLinesでは、ソースコードを改良しない限り、投票値そのものをとることはできません。
しかし、内部の実装hough.cpp l.190を見ると、
// stage 3. sort the detected lines by accumulator value
std::sort(_sort_buf.begin(), _sort_buf.end(), hough_cmp_gt(accum));
のように投票値が大きい順にソートしてくれていることが分かります。
ですので、結果のlinesを前から順に取り出すことで、直線らしさが大きい順に、直線を抜き出すことができます。
まとめ
如何でしたでしょうか?ちょっと長い記事になってしまいましたが、画像からの直線検出のスタンダードな手法としてのHough変換について、初学者向きに丁寧に解説してみました。初学者の方からのご意見お待ちしています。また、独自の解釈もありますので、有識者の方からも、ご指摘等お聞かせ願えれば幸いです。