10月ぐらいですかね。なんでだかわからないのですが、多重比較について生物系や農業系などの大学院に通っている友人複数から質問を受けました。
僕個人的には多重比較自体あまり好きではありませんし、それをやる意味もあまり見いだせていなかったので避けてきましたが、聞かれてしまったので色々調べてみました。教科書を使って体系的に学習したわけではなく、Google検索してそれっぽいのをつまみ食いしまくったというところですかね。
調べている中で出てきたものを読んだり、質問をしてくれた人にどう教わっているのか聞いたりしている中で、それって多重比較している意味大丈夫なの?と疑問に思うことがあったので、多重比較の概要に触れながらシミュレーションレベルでその疑問を確認してみたいと思います。
そもそも多重比較って。。。?
そもそも多重比較とは何なのか簡単に紹介します。
例えば2つの母集団 $A,B$ の平均 $\mu_A,\mu_B$ を比較する方法を考えます。
この場合、(色々な仮定があるものの)まず真っ先に思い浮かべる方法は $t$ 検定だと思います。
※そもそも検定ってなんだ?という方はこの辺りを参考にしていただければなと…
・検定とはなんぞや
・有意水準とp値とは結局何なのか
では、3つの母集団 $A,B,C$ の平均 $\mu_A,\mu_B,\mu_C$ を比較する方法はどうでしょうか?
安直に思いつくことは、$\mu_A$と$\mu_B$、$\mu_A$と$\mu_C$、$\mu_B$と$\mu_C$についてそれぞれ $t$ 検定を行うことです。
例えば$\mu_A$と$\mu_B$だけに有意差が認められ、残りの2つの検定に関しては有意差がなかった場合、$\mu_A$と$\mu_B$ には差があるが、$\mu_A$と$\mu_C$、$\mu_B$と$\mu_C$には差があるとは言えないとしてしまうという具合です。これを多重比較といいます。
しかし、この方法には大きな問題があります。
多重比較の問題点
今、独立な3つの検定 $H_1,H_2,H_3$ を実行することを考えます。
神のみぞ知る結論を「3つの検定における帰無仮説は全て正しい」とした場合、
それぞれの検定の有意水準を全て0.05に設定して3つの検定を実行すると、$H_1,H_2,H_3$ のうち少なくとも1つは帰無仮説が棄却される確率は、$1-0.95^3≒0.143$ となります[^1]。
つまり、$H=\{H_1,H_2,H_3\}$ と、一連の手続きを $H$ という大きな枠組みとしてとらえると、帰無仮説が正しい場合でも、誤って帰無仮説を棄却してしまう確率は約14%になってしまうということです。
$H$ が $N$個の独立な検定を実施している場合はどうなるでしょうか?
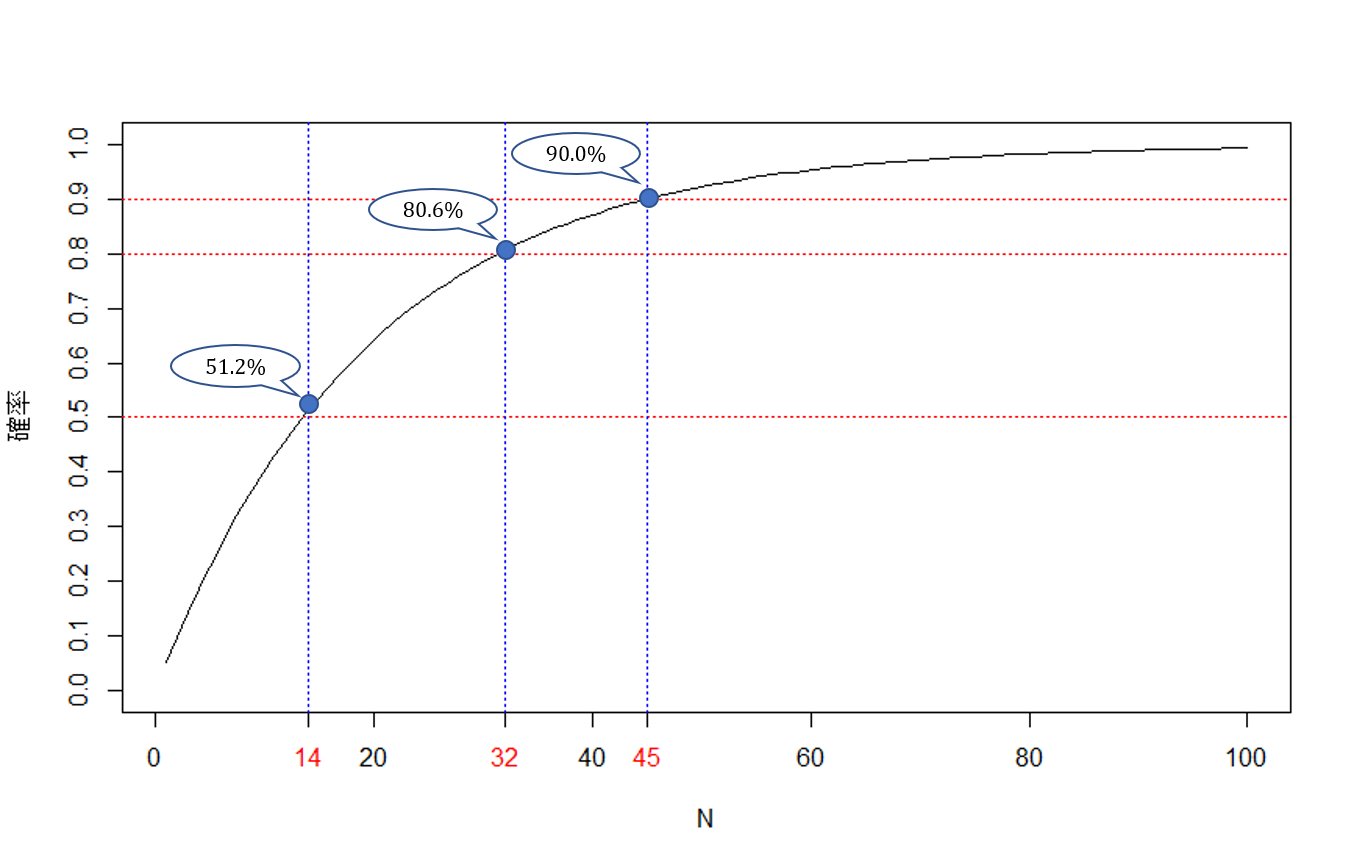
この場合、 $H_1,...,H_N$ のうち少なくとも1つは帰無仮説が棄却される確率は、$1-0.95^N$ となります。シミュレーションで $N=1~100$ まで確認してみると次のようになります。
今回はRを使っています。
f = function(x){
1-0.95^x
}
# N=1~100まで計算する
P = numeric(100)
for(i in 1:100){
P[i] = f(i)
}
P
=== 実行結果 ==============================
[1] 0.0500000 0.0975000 0.1426250 0.1854938 0.2262191 0.2649081 0.3016627 0.3365796 0.3697506 0.4012631 0.4311999
[12] 0.4596399 0.4866579 0.5123250 0.5367088 0.5598733 0.5818797 0.6027857 0.6226464 0.6415141 0.6594384 0.6764665
[23] 0.6926431 0.7080110 0.7226104 0.7364799 0.7496559 0.7621731 0.7740645 0.7853612 0.7960932 0.8062885 0.8159741
[34] 0.8251754 0.8339166 0.8422208 0.8501097 0.8576043 0.8647240 0.8714878 0.8779135 0.8840178 0.8898169 0.8953260
[45] 0.9005597 0.9055318 0.9102552 0.9147424 0.9190053 0.9230550 0.9269023 0.9305572 0.9340293 0.9373278 0.9404614
[56] 0.9434384 0.9462665 0.9489531 0.9515055 0.9539302 0.9562337 0.9584220 0.9605009 0.9624759 0.9643521 0.9661345
[67] 0.9678277 0.9694364 0.9709645 0.9724163 0.9737955 0.9751057 0.9763504 0.9775329 0.9786563 0.9797235 0.9807373
[78] 0.9817004 0.9826154 0.9834846 0.9843104 0.9850949 0.9858401 0.9865481 0.9872207 0.9878597 0.9884667 0.9890434
[89] 0.9895912 0.9901116 0.9906061 0.9910758 0.9915220 0.9919459 0.9923486 0.9927311 0.9930946 0.9934399 0.9937679
[100] 0.9940795
===========================================
14個の検定で50%を超え、32個の検定で80%、45個の検定で90%を超えます。
強調したいのは、神のみぞ知る真実は「帰無仮説は全て正しい」であるにもかかわらず、検定を繰り返すと間違った結論を下す確率がどんどん大きくなるということです。
これではとてもじゃないですけど、良い検定であるとは言い難いですよね。
分散分析
多重比較の問題を回避する、というか3つ以上の母集団の平均を比較する問題は、基本的には分散分析によって解析します。
まぁ、でも、多重検定とは目的が異なるので注意が必要です。
分散分析は実験計画法の文脈で語られることが多いのですが、ここでは分散分析そのものだけに着目して簡単に説明します。
$d$個の母集団 $A_1,...,A_d$ の平均 $\mu_1,...,\mu_d$ を比較する問題を考えます。
(markdownで罫線って書けないのかな。。。)
ここで、
\hat{\mu_i}=\frac{1}{n}\sum_{k=1}^{n}x_{ni} (i=1,...,d)
です。つまり$\hat{\mu_i}$は各列の単純平均です。
さて、分散分析の目的は $\mu_1,...,\mu_d$ は全て同じかどうかを判定することです。つまり帰無仮説 $H_0$ と対立仮説 $H_1$ は次のようになります。
$H_0:\mu_1=・・・=\mu_d$
$H_1:\mu_1,...,\mu_d$ の中に異なるものが少なくとも1つは存在する。
※分散分析の詳細については、インターネット上にたくさん優れた記事や講義ノートやPDF資料があるのでそちらを参照してください。
分散分析でわかるのは「全部の平均が同じわけじゃないんだね」というところまでです。
もう少し詳しく実験計画法っぽく言うと「どの要因に効果があるか」ということです。
どの平均とどの平均が違うのかを判定する方法ではありません。
◆簡単な例
簡単な例として、化学反応する量が反応させる温度で変化するかという問題を考えます。$A_i(i=1,...,d)$を化学反応させる温度として、次のようなデータが得られたとします。
このデータを基に分散分析を実行して有意になった場合、得られる結論は「化学反応する量は、化学反応させる温度の効果を受ける」というところまでです。
◆簡単なシミュレーション
今、$3$つの標本 $a$ と $b$ と $c$ の平均に差があるかを調べたいとします。
神のみぞ知る結論を先にカンニングしておくと、次のようになっています。
$\qquad \qquad a\sim N(50,10)$
$\qquad \qquad b\sim N(50,10)$
$\qquad \qquad c\sim N(50,10)$
御覧の通りすべて同じ平均と分散を持つ正規分布から生成されています。
分散分析は標本がデータが正規分布に従い、かつ各母集団の分散は同じだと仮定して行われるため、今回このように設定しました。
1回の分析で $a,b,c$ それぞれ$10$個ずつデータを抽出して、分散分析を$1$万回実施し、どれくらいの割合で有意になるかを調べます。
m = 0
l = 0
for (i in 1:10000){
a <- rnorm(10, mean=50, sd=10)
b <- rnorm(10, mean=50, sd=10)
c <- rnorm(10, mean=50, sd=10)
A <- data.frame(ID=rep("A",10), data=a)
B <- data.frame(ID=rep("B",10), data=b)
C <- data.frame(ID=rep("C",10), data=c)
X <- rbind(A,B,C)
out <- anova(aov(data~ID, data=X))$Pr[1]
if (out < 0.05){m = m+1}
else{l = l+1}
}
P = m/(m+l) # 帰無仮説を棄却した割合
P
=== 実行結果 ==============================
[1] 0.0494
===========================================
だいたい$5$%ぐらいの割合で有意になるみたいですね。
このように帰無仮説が正しくても、$5$%ぐらいの確率で誤って帰無仮説を棄却してしまうということをこのシミュレーションは言っています。
皆さんがよく知っている一般的な検定と同じですね。
多重比較の方法:Bonferroniの方法
分散分析では「どの要因に効果があるか」ということがわかるのでした。
ではその要因のどの水準とどの水準に差があるのかという問題にはどのように対処すればよいでしょうか?という最初の問題を再び考えてみます。
先に示した通り、$t$検定を$3$回実施するのは第1種の過誤の観点から非常にまずいです。
では第1種の過誤の問題に対処してみるというのはどうでしょうか?
この発想をしているのがBonferroniの方法です。
Bonferroniの方法は、確率の基本性質である
P( \bigcup_{k=1}^n A_k )≤\sum_{k=1}^{n}P(A_k)
を基に考えます。
$H=\{H_1,...,H_d\}$ のように$d$ 個の検定を実施し、これら一連の手続きを一つの検定$H$とします。
$d$ 個の帰無仮説が全て正しい場合に、検定$H$ において第1種の過誤が起こる確率を$5$%以下に抑えるのに上の不等式を使います。
各検定$H_i (i=1,...,d)$で第1種の過誤が起きる確率を $P(\hat{H_i}=1|H_i=0)$ と書くことにすると、
※表記について、一般的ではないと思うので補足します。
$H_i$ :神のみぞ知る真実。
・$0$:仮説は真
・$1$:仮説は偽
$\hat{H_i}$ :検定による結果
・$0$:帰無仮説を採択
・$1$:帰無仮説を棄却
P( \bigcup_{i=1}^d \{\hat{H_i}=1|H_i=0\} )≤\sum_{i=1}^{d}P(\{\hat{H_i}=1|H_i=0\})
という不等式が成り立ちます。今、各検定$H_i (i=1,...,d)$ の有意水準は $0.05$ なので、この不等式は具体的に次のように書けます。
P( \bigcup_{i=1}^d \{\hat{H_i}=1|H_i=0\} )≤0.05×d
両辺 $d$ で割ると、
\frac{1}{d}P( \bigcup_{i=1}^d \{\hat{H_i}=1|H_i=0\} )≤0.05
となります。
つまり、各有意水準を検定の回数で割ることによって検定全体(つまり検定 $H$ )の第1種の過誤を犯す確率を$0.05$以下に抑えることができます。
◆簡単なシミュレーション
設定は分散分析と同じです。
$3$つの標本 $a$ と $b$ と $c$ の平均に差があるかを調べたいとします。
神のみぞ知る結論を先にカンニングしておくと、次のようになっています。
$\qquad \qquad a\sim N(50,10)$
$\qquad \qquad b\sim N(50,10)$
$\qquad \qquad c\sim N(50,10)$
御覧の通りすべて同じ平均と分散を持つ正規分布から生成されています。
1回の分析で $a,b,c$ それぞれ$10$個ずつデータを抽出して、Bonferroni の方法で $t$ 検定を$1$万回実施し、どれくらいの割合で少なくとも1つは有意になるかを調べます。
m = 0
l = 0
for (i in 1:10000){
a <- rnorm(10, mean=50, sd=10)
b <- rnorm(10, mean=50, sd=10)
c <- rnorm(10, mean=50, sd=10)
A <- data.frame(ID=rep("A",10), data=a)
B <- data.frame(ID=rep("B",10), data=b)
C <- data.frame(ID=rep("C",10), data=c)
X <- rbind(A,B,C)
out <- pairwise.t.test(X$data, X$ID, paired=F, p.adj="bonferroni", data=X)
if (out$p.value[1] < 0.05||out$p.value[2] < 0.05||out$p.value[4] < 0.05){m = m+1}
else{l = l+1}
}
P = m/(m+l) # 帰無仮説を棄却した割合
P
=== 実行結果 ==============================
[1] 0.0442
===========================================
だいたい$4.4$ %ぐらいの割合で少なくとも$1$つは有意になるみたいですね。
たしかに補正はうまくいっているようです。
※注意
Bonferroni の方法は確かに第1種の過誤の確率は小さくできますが、保守的すぎるという難点を抱えています。
検出力(神のみぞ知る真実は帰無仮説が偽である時に、検定によって誤って帰無仮説を棄却してしまう確率)も悪化します。
もちろんこれらを改善した検定手法も考案されていますが、今回は省略します。
やっと本題:今回の疑問
やっとこさ本題です。
そもそも今回記事にしようと思ったのは、この疑問からです。
それは友人の大学院生から多重比較について話を聞いた時、複数人が「分散分析で有意だった時に多重比較を行う」というようなことを言っていたことに疑問を持ったからというものです。
というのもこれも結局は 分散分析 ⇒ 多重比較 という多重検定の問題を抱えているのではないか?という疑問です。
(この場合、単純に分散分析が有意になったという条件が加わるだけなので、第1種の過誤の確率が小さくなるはずです。)
たぶん、僕の考えている通りなんですけど、シミュレーションでも確認してみます。
m = 0
l = 0
for (i in 1:10000){
a <- rnorm(10, mean=50, sd=10)
b <- rnorm(10, mean=50, sd=10)
c <- rnorm(10, mean=50, sd=10)
A <- data.frame(ID=rep("A",10), data=a)
B <- data.frame(ID=rep("B",10), data=b)
C <- data.frame(ID=rep("C",10), data=c)
X <- rbind(A,B,C)
out <- pairwise.t.test(X$data, X$ID, paired=F, p.adj="bonferroni", data=X)
Pout <- min(c(out$p.value[1], out$p.value[2], out$p.value[4]))
ANOVAout <- anova(aov(data~ID, data=X))$Pr[1]
if ((out$p.value[1] < 0.05||out$p.value[2] < 0.05||out$p.value[4] < 0.05)&&(ANOVAout < 0.05)){m = m+1}
else{l = l+1}
}
P = m/(m+l) # 帰無仮説を棄却した割合
P
=== 実行結果 ==============================
[1] 0.0399
===========================================
分散分析で有意となった場合にBonferroniの方法で多重比較を行うと、第1種の過誤を犯す確率は $4$% 程になるみたいです。
__Bonferroni__の方法単独での分析と比較してみます。

やはりかなり保守的になっているということですね。
##まとめ
散々長々と書きましたが、やはり分散分析で有意になった後に多重比較をするというのは良くないみたいです。
(まぁ、分散分析もBonferroniの枠組みの中に入れてしまえば、、、でもBonferroni自体も保守的だからなぁ、、、)
そもそも初めからどの母集団とどの母集団に差があるのか知りたいのであれば、分散分析は不要で多重比較だけすればよいと思います。
◆ちなみに...
ちなみに私は多重検定をほとんどしたことがないです。。。
★参考文献★
[1]野田,宮岡:数理統計学の基礎(1992)
[2]藤田:大学生の確率・統計(2010)
[4]間瀬,神保,鎌倉,金藤:工学のためのデータサイエンス入門(2004)
[5]対馬:多重比較(URL:https://personal.hs.hirosaki-u.ac.jp/pteiki/research/stat/multi.pdf)