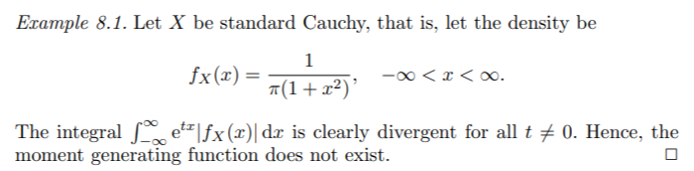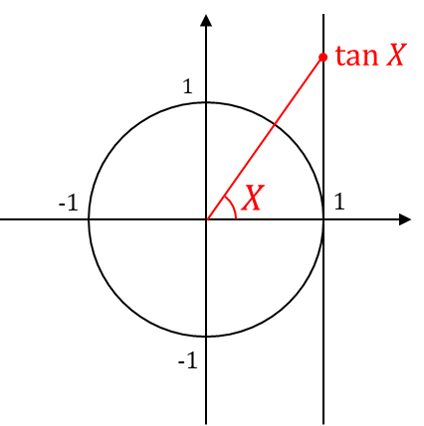コーシー分布について調べる必要があり、色々Google先生に聞いていました。
なのですが、ほとんどが期待値と分散が存在しないという話しか教えてくれず、かなり苦戦しました。
Wikipediaが一番詳しかったような感じがしましたが、計算方法とかは載っていないからモヤモヤするし、英語の文献とかだと詳しいのあったけど、そもそも英語読むの大変だし。。。
日本語である程度まとまっているのが読めたら、何人かはハッピーになるかなということで、今回はコーシー分布について書いていこうと思います。
1.確率密度関数
コーシー分布の確率密度関数は、以下で与えられます。
f(x) = \frac{1}{\pi \left( 1+x^2 \right)} \;\;\; (-\infty < x < \infty) \tag{1.1}
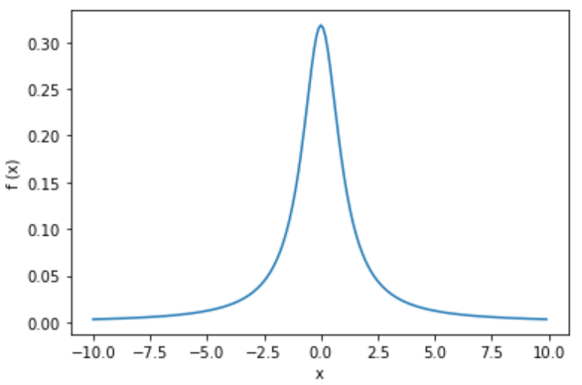
確率密度関数の形は、こんな感じ。
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-10, 10, 0.1)
y = 1 / (np.pi * (1 + x**2))
plt.plot(x, y)
plt.ylabel("f (x)")
plt.xlabel("x")
plt.show()
これが確率密度関数であることは、次のようにして分かります。
\begin{eqnarray}
\int_{-\infty}^{\infty} f(x) \, dx &=& \int_{-\infty}^{\infty} \frac{1}{\pi \left( 1+x^2 \right)} \, dx \\
\\
&=& \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1}{\pi \left( 1+ \tan^2 \theta \right)} \frac{d\theta}{\cos^2 \theta} \,\,\,\,\,\,\, (x=\tan\theta \, で置換)\\
\\
&=& \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1}{\pi \left( \frac{1}{\cos^2 \theta} \right)}\frac{d\theta}{\cos^2 \theta}\\
\\
&=& \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1}{\pi} \, d\theta \\
\\
&=& 1 \tag{1.2}
\end{eqnarray}
次に分布関数 $P(X≤x)=F(x)$ について考えます。
\begin{eqnarray}
F(x) &=& \int_{- \infty}^{x} f(t) \, dt \\
\\
&=& \int_{- \infty}^{x} \frac{1}{\pi \left( 1+t^2 \right)} \, dt \\
\\
&=& \frac{1}{\pi} \, \Bigl[\, \arctan t \, \Bigl]_{- \infty}^{\,x} \\
\\
&=& \frac{1}{\pi} \, \left( \, \arctan x + \frac{\pi}{2} \, \right) \\
\\
&=& \frac{1}{\pi} \arctan x + \frac{1}{2} \tag{1.3}
\end{eqnarray}
もちろん、確率密度関数であることを確認した時と同じように、$t=\tan{\theta}$ で置換しても同じように求まります。その場合は、
\begin{eqnarray}
F(x) &=& \int_{- \infty}^{x} f(t) \, dt \\
\\
&=& \int_{- \infty}^{x} \frac{1}{\pi \left( 1+t^2 \right)} \, dt \\
\\
&=& \int_{-\frac{\pi}{2}}^{\arctan{x}} \frac{1}{\pi \left( 1+ \tan^2 \theta \right)} \frac{d\theta}{\cos^2 \theta} \\
\\
&=& \int_{-\frac{\pi}{2}}^{\arctan{x}} \frac{1}{\pi} \, d\theta \\
\\
&=& \frac{1}{\pi} \, \left( \, \arctan x + \frac{\pi}{2} \, \right) \\
\\
&=& \frac{1}{\pi} \arctan x + \frac{1}{2} \tag{1.4}
\end{eqnarray}
確率密度関数の計算も、分布関数の計算も少しだけテクニカルなことをしていますが、高校数学で習ったものや大学初年度で習ったものなので安心してください。
このあたりが参考になると思います↓↓
<< 参考 >>
・具体例で学ぶ数学
・理系大学生の数学駆け込み寺
また、一般化して、位置母数 $-\infty < \mu < \infty$、尺度母数 $\sigma > 0$ のコーシー分布は、
\begin{eqnarray}
f(x \,|\, \mu,\sigma) &=& \frac{\sigma}{\pi \left \{ \sigma^2 + \left( x - \mu \right)^2 \right \} } \tag{1.4}\\
\\\\
P(X≤x \,|\, \mu,\sigma) &=& F(x\,|\, \mu,\sigma)\\
\\
&=& \frac{1}{\pi} \arctan \left( \frac{x - \mu}{\sigma} \right) + \frac{1}{2} \tag{1.5}
\end{eqnarray}
となります。位置母数 $\mu$ は、最頻値や中央値を与え、尺度母数 $\sigma$ は、半値半幅を与えます。
$\mu=0$、$\sigma=1$ の時が式 $(1.1)$ で、標準コーシー分布といいます。
この記事では、標準コーシー分布について扱い、標準コーシー分布のことを単にコーシー分布と呼ぶことにします。
2.期待値
これは超有名な話。
コーシー分布の存在意義が、期待値と分散が存在しない分布の例になっている、という点しかないのでは?と思ってしまうほどです。
超有名な話のため、コーシー分布をググると大抵この話がヒットしますが、この記事は自分用のメモという意味もあるので、ここでも丁寧に計算しておこうと思います。
\begin{eqnarray}
E[X] &=& \int_{-\infty}^{\infty} xf(x)\,dx \\
\\
&=& \int_{-\infty}^{\infty} x \, \frac{1}{\pi \left( 1+x^2 \right)} \, dx \\
\\
&=& \frac{2}{\pi} \int_{0}^{\infty} \, \frac{x}{\left( 1+x^2 \right)} \, dx > \frac{2}{\pi} \int_{\color{red}{1}}^{\infty} \, \frac{x}{ \left( 1+x^2 \right)} \, dx \tag{2.1}\\
\end{eqnarray}
ここで、$x≥1$ に対して、$\frac{x}{1+x^2} ≥ \frac{1}{2x}$ だから、式 $(2.1)$ は、
\begin{eqnarray}
E[X]= \frac{2}{\pi} \int_{0}^{\infty} \, \frac{x}{\pi \left( 1+x^2 \right)} \, dx &>& \frac{2}{\pi} \int_{1}^{\infty} \, \color{red}{\frac{x}{ \left( 1+x^2 \right)}} \, dx \tag{2.1} \\
\\
&>& \frac{2}{\pi} \int_{1}^{\infty} \, \color{red}{\frac{1}{2x}} \, dx \\
\\
&=& \frac{2}{\pi} \, \Bigl[\, \log{x} \, \Bigl]_{1}^{\infty} \\
\\
&=& \infty \tag{2.2} \\
\end{eqnarray}
これより、期待値は存在しないことが分かります。
期待値が存在しないので、2次以降の中心積率($k$ 次の中心積率:$E[(X-\mu)^k]$ )も存在しません。従って、分散も歪度も尖度も存在しません。
分散は存在しませんが、2次モーメントは考えることができます。しかし、これも無限大になってしまいます。
\begin{eqnarray}
E[X^2] &=& \int_{-\infty}^{\infty} x^2 f(x)\,dx \\
\\
&=& \int_{-\infty}^{\infty} \frac{x^2}{\pi \left( 1+x^2 \right)} \, dx \\
\\
&=& 2 \int_{0}^{\infty} \frac{x^2}{\pi \left( 1+x^2 \right)} \, dx \\
\\
&=& \frac{2}{\pi} \int_{0}^{\infty} \frac{(1-1)+x^2}{ 1+x^2 } \, dx \\
\\
&=& \frac{2}{\pi} \int_{0}^{\infty} \left\{ \frac{ 1+x^2 }{ 1+x^2 } - \frac{1}{ 1+x^2 } \right\} dx \\
\\
&=& \frac{2}{\pi} \left\{ \int_{0}^{\infty} dx - \int_{0}^{\infty} \frac{1}{ 1+x^2 } \, dx \right\}\\
\\
&=& \frac{1}{\pi} \Bigl\{ \bigl[ x \bigl]_{0}^{\infty} - \bigl[\arctan (1+x^2)\bigl]_{0}^{\infty} \Bigl\}\\
\\
&=& \infty \, - \pi \\
\\
&=& \infty \tag{2.3}
\end{eqnarray}
3.積率母関数(モーメント母関数)
コーシー分布は、積率母関数まで持っていません。なんて不便なんだ。。。
wikipediaにあった、参考文献(Allan Gut: Probability: A Graduate Course)を覗いてみたのですがよくわからず。
(「Allan Gut: Probability: A Graduate Course pdf」で検索すると出てきます。617ページあるので開く際は注意が必要です。)
ちなみにそこでは、このように書いてあります↓↓
clearly divergent って書いてあるんですけど、数弱なのでどこがclearlyなのかよくわからないんですよね。
\begin{eqnarray}
M_X(t) = E[e^{tX}] &=& E\left[\sum_{k=0}^{\infty}\frac{(tX)^k}{k!}\right] \\
\\
&=& E[\,1\,] + E[\,tX\,] + E\left[\frac{1}{2}(tX)^2\right] + E\left[\frac{1}{6}(tX)^3\right] + ・・・\\
\\
&=& E[\,1\,] + tE\left[X\right] + \frac{t^2}{2} E\left[X^2\right] + \frac{t^3}{6} E\left[X^3\right] + ・・・
\end{eqnarray}
だから、$t=0$ だと $M_X(0) = E[,1,] = 1$ で求まるけど、$t≠0$ だと1次以降のモーメントは発散しているから $M_X(t)$ は求まらないという認識でいいのかな・・・?
4.コーシー分布を作る。
ここでは、確率変数をガチャガチャいじったらコーシー分布に従う例をいくつか紹介します。
① $X$ と $Y$ を標準正規分布に独立に従う確率変数とした時、$\frac{X}{Y}$ は、コーシー分布に従います。
\begin{eqnarray}
f_{\frac{Y}{X}}(x) &=& \int_{-\infty}^{\infty} f_X(u) f_Y(ux) |u| du \\
\\
&=& \int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi}} e^{- \frac{u^2}{2}} \frac{1}{\sqrt{2\pi}} e^{- \frac{u^2x^2}{2}} |u| du \\
\\
&=& \frac{1}{2\pi} \int_{-\infty}^{\infty} |u| e^{- \frac{1+x^2}{2} u^2} du\\
\\
&=& \frac{1}{\pi} \int_{0}^{\infty} u e^{- \frac{1+x^2}{2} u^2} du\\
\\
&=& \frac{1}{\pi} \left[ - \frac{1}{1+x^2} e^{- \frac{1+x^2}{2} u^2} \right]_{0}^{\infty} \\
\\
&=& \frac{1}{\pi(1+x^2)} \tag{4.1}
\end{eqnarray}
② 自由度 $1$ の $t$ 分布は、コーシー分布です。
自由度 $n$ の $t$ 分布の確率密度関数は、
\begin{eqnarray}
f_{t_n} &=& \frac{\Gamma \left( \frac{n+1}{2} \right)}{\sqrt{n \pi} \, \Gamma \left( \frac{n}{2} \right)} \left( 1 + \frac{x^2}{n} \right)^{- \frac{n+1}{2}} \,\,\,\,, - \infty < x < \infty \tag{4.2}
\end{eqnarray}
です。なので、自由度 $n=1$ の時は、
\begin{eqnarray}
f_{t_1} &=& \frac{1}{\sqrt{\pi} \, \sqrt{\pi}} (1+x^2)^{-1} \,\,\,\,, - \infty < x < \infty \\
\\
&=& \frac{1}{\pi(1+x^2)} \tag{4.3}
\end{eqnarray}
③ 確率変数 $X$ がコーシー分布に従う時、$\frac{1}{X}$ もコーシー分布に従います。
\begin{eqnarray}
P\left( \frac{1}{X} ≤ y \right) &=& P\left( \frac{1}{y} ≤ X \right)\\
\\
&=& 1-P\left( X< \frac{1}{y} \right) \\
\\
&=& 1-F_X\left( \frac{1}{y} \right) \\
\\
&=& 1- \int_{-\infty}^{\frac{1}{y}} \frac{1}{\pi(1+x^2)} \, dx \\
\\
f_{\frac{1}{X}}(y) &=& \frac{d}{dy} P\left( \frac{1}{X} ≤ y \right) \\\
\\
&=& -\frac{1}{\pi \left(1+\frac{1}{y^2} \right)} × \left(- \frac{1}{y^2} \right) \\
\\
&=& \frac{1}{\pi (1+y^2)} \tag{4.4}
\end{eqnarray}
④ $X$ が区間 $\left(-\frac{\pi}{2},\frac{\pi}{2}\right)$ 上で一様に分布している時、$\tan X$ はコーシー分布に従います。
このことは、式 $(1.2)$ の計算過程を見るとなんとなくわかると思います。
(ちなみに言っていることのイメージは、例えばこんな感じです。)
$\tan X$ がコーシー分布に従うことは、次のようにして分かります。
まず、
\begin{eqnarray}
P(\tan X ≤ x) &=& P(X ≤ \arctan x) \\
\\
&=& \int_{-\frac{\pi}{2}}^{\arctan x} f_X(t) dt \\
\\
&=& \int_{-\frac{\pi}{2}}^{\arctan x} \frac{1}{\pi} dt \\
\\
&=& \left[\,\frac{1}{\pi} t \, \right]^{\arctan x}_{-\frac{\pi}{2}}\\
\\
&=& \frac{1}{\pi} \left(\arctan x + \frac{\pi}{2}\right) \tag{4.5}
\end{eqnarray}
もちろん、$\tan x$ の確率密度関数は、
\begin{eqnarray}
f_{\tan X}(x) &=& \frac{d}{dx} P(\tan X ≤ x) \\
\\
&=& \frac{d}{dx} \left\{ \frac{1}{\pi} \left(\arctan x + \frac{\pi}{2}\right) \right\} \\
\\
&=& \frac{1}{\pi (1+x^2)} \tag{4.6}
\end{eqnarray}
# 5.特性関数
コーシー分布は、平均や分散、積率母関数は存在しませんが、特性関数は定義できます。
コーシー分布の特性関数は、留数定理を使って導出するのが一般的ですが、久保川数理統計学のサポートページ のP28に留数定理を使わない方法が載っていました。しかも2パターンも!
ここでは、私がかっこいいと感じた[解法1]のアウトラインを紹介したいと思います。
まず、式 $(4.1)$ で見たように、標準正規分布に独立に従う2つの確率変数 $X,Y$ の商 $Z=\frac{X}{Y}$ がコーシー分布に従うところから始まります。
次に、特性関数 $\phi_Z(t)$ を条件付き期待値を使って、
\phi_Z(t)=E\Bigl[E\bigl[e^{it\frac{X}{Y}} \bigl|Y\bigl]\Bigl] \tag{5.1}
で表します。
すると、この内側の期待値の計算は、$X$ が標準正規分布に従っているので、標準正規分布の特性関数が
\phi_{N(0,1)}(t)=e^{-\frac{t^2}{2}} \tag{5.2}
であることを使って、
E\Bigl[e^{it\frac{X}{Y}} \, \Bigl| \, Y \Bigl] = e^{-\frac{1}{2}\left(\frac{t}{Y} \right)^2} \tag{5.3}
と求まります。あとはこの期待値を計算すればいいのですが、この計算テクニックもすごくて、
よしなに変数変換をすると、逆ガウス分布の確率密度関数が現れ、積分するときれいに1になってくれたり、かくかくしかじかあって、結果的に
\phi_{Z}(t)=e^{|t|} \tag{5.4}
が得られます。
鮮やかですね。
詳しくは、久保川数理統計学のサポートページ を参照してください。
6.標本平均の分布
コーシー分布は期待値を持ちませんが、標本平均の分布は考えることができます。
$X_1,X_2,\cdots,X_n$ をコーシー分布に従う互いに独立な確率変数とすると、標本平均の特性関数は、
\begin{eqnarray}
\phi_{\bar{X}}(t) &=& E\left[\, e^{i \bar{X} t} \, \right] \\
\\
&=& E\left[\,e^{i \frac{X_1+X_2+\cdots+X_n}{n}t} \, \right] \\
\\
&=& E\left[\,e^{i \frac{X_1}{n} t}\right] × E\left[\,e^{i \frac{X_2}{n} t}\right] × \cdots × E\left[\,e^{i \frac{X_n}{n} t}\right]\\
\\
&=& E\left[\,e^{i \frac{X_1}{n} t}\right]^n\\
\\
&=& E\left[\,e^{i X_1 t}\right]\\
\\
&=& \phi_{X_1}(t) \tag{6.1}
\end{eqnarray}
となり、標本平均がコーシー分布に従うことが分かります。
また、この計算からコーシー分布は再生性を持つことも分かります。
7.エントロピー
エントロピーの計算は思っていたよりも大変でした。。。
$X$ がコーシー分布に従う時、エントロピーを $H$ で表すと、
\begin{eqnarray}
H &=& - \int_{- \infty}^{\infty} f_X(x) \log{f_X(x)} dx \\
\\
&=& - \int_{- \infty}^{\infty} \frac{1}{\pi(1+x^2)} \log{\frac{1}{\pi (1+x^2)}} dx \\
\\
&=& \int_{- \infty}^{\infty} \frac{1}{\pi(1+x^2)} \log{\pi (1+x^2)} dx \\
\\
&=& \int_{- \infty}^{\infty} \frac{1}{\pi(1+x^2)} \log{\pi (1+x^2)} dx \\
\\
&=& \int_{- \infty}^{\infty} \frac{1}{\pi(1+x^2)} \Bigl\{ \log{\pi} + \log{(1+x^2)} \Bigl\} dx \\
\\
&=& \frac{1}{\pi} \left\{ \int_{- \infty}^{\infty} \frac{1}{(1+x^2)} \log{\pi} dx + \int_{- \infty}^{\infty} \frac{\log{(1+x^2)}}{1+x^2} dx \right\}\\
\\
&=& \frac{1}{\pi} \left\{ \log{\pi} \Bigl[\arctan{x} \Bigl]_{-\infty}^{\infty} + \int_{- \infty}^{\infty} \frac{\log{(1+x^2)}}{1+x^2} dx\right\} \\
\\
&=& \frac{1}{\pi} \left\{\pi\log{\pi} + \color{red}{\int_{- \infty}^{\infty} \frac{\log{(1+x^2)}}{1+x^2} dx} \right\} \tag{7.1}\\
\end{eqnarray}
ここで、式 $(7.1)$ の赤文字部分は多少の工夫を施した計算が必要です。
I=\color{red}{\int_{- \infty}^{\infty} \frac{\log{(1+x^2)}}{1+x^2} dx} \tag{7.2}
とおき、$x=\tan\theta$ で置換すると、
\begin{eqnarray}
I &=& \color{red}{\int_{- \infty}^{\infty} \frac{\log{(1+x^2)}}{1+x^2} dx}\\
\\
&=& - \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \log{(\cos^2\theta)} d\theta\\
\\
&=& -2\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \log{(\cos\theta)} d\theta\\
\\
&=& -4\int_{0}^{\frac{\pi}{2}} \log(\cos\theta) d\theta \tag{7.3}
\end{eqnarray}
ここで、
\int_{0}^{\frac{\pi}{2}} \log(\cos\theta) d\theta = \int_{0}^{\frac{\pi}{2}} \log(\sin\theta) d\theta \tag{7.4}
なので($\theta = \frac{\pi}{2}-y$ と置換して確かめられます)、式 $(7.3)$ は、次のように書き換えられます。
\begin{eqnarray}
I &=& -4\int_{0}^{\frac{\pi}{2}} \log(\cos\theta) d\theta \\
\\
&=& -4\int_{0}^{\frac{\pi}{2}} \log(\sin\theta) d\theta\tag{7.5}
\end{eqnarray}
ここから、少し頑張ります。
\begin{eqnarray}
2I &=& \left\{-4\int_{0}^{\frac{\pi}{2}} \log(\cos\theta) d\theta\right\} + \left\{-4\int_{0}^{\frac{\pi}{2}} \log(\sin\theta) d\theta\right\}\\
\\
&=& -4 \int_{0}^{\frac{\pi}{2}} \Bigl\{\log(\cos\theta) + \log(\sin\theta)\Bigl\} d\theta \\
\\
&=& -4 \int_{0}^{\frac{\pi}{2}} \log(\cos\theta\sin\theta) d\theta \\
\\
&=& -4 \int_{0}^{\frac{\pi}{2}} \log(\frac{1}{2}\,\sin2\theta) d\theta \\
\\
&=& -4 \left\{\int_{0}^{\frac{\pi}{2}} \log(\sin2\theta) d\theta-\int_{0}^{\frac{\pi}{2}} \log2 \, d\theta\right\}\\
\\
&=& -4 \left\{\int_{0}^{\frac{\pi}{2}} \log(\sin2\theta) d\theta - \frac{\pi}{2} \log2 \right\} \tag{7.6}
\\
\end{eqnarray}
$2\theta=t$ と置換すると、
\begin{eqnarray}
2I &=& -4 \left\{\frac{1}{2} \int_{0}^{\pi} \log(\sin t) dt - \frac{\pi}{2} \log2 \right\}\\
\\
&=& -4 \left\{\frac{1}{2} \Bigl(\int_{0}^{\frac{\pi}{2}} \log(\sin t) dt + \color{Blue}{\int_{\frac{\pi}{2}}^{\pi} \log(\sin t) dt} \Bigl) - \frac{\pi}{2} \log2 \right\}\\
\\
&=& -4 \left\{\frac{1}{2} \Bigl(\int_{0}^{\frac{\pi}{2}} \log(\sin t) dt + \color{Blue}{\int_{0}^{\frac{\pi}{2}} \log(\sin t) dt} \Bigl) - \frac{\pi}{2} \log2 \right\}\\
\\
&=& -4 \left\{\frac{1}{2} × 2 \int_{0}^{\frac{\pi}{2}} \log(\sin t) dt - \frac{\pi}{2} \log 2 \right\}\\
\\
&=& -4 \left\{\frac{1}{2} × \left(-\frac{1}{2}\right) \left(-4\int_{0}^{\frac{\pi}{2}} \log(\sin t) dt \right) - \frac{\pi}{2} \log 2 \right\}\\
\\
&=& -4 \left\{\frac{1}{2} × \left(-\frac{1}{2}\right)I - \frac{\pi}{2} \log 2 \right\}\\
\\
&=& I + 2\pi \log 2 \\
\\
\therefore \, I &=& 2\pi \log 2 \tag{7.7} \\
\end{eqnarray}
※青文字の部分は、$u=\pi-\theta$ と置換することで確認することができます。
これでやっと式 $(7.1)$ の $I$ に代入できるようになりました。
式 $(7.6)$ を式 $(7.1)$ に用いると、
\begin{eqnarray}
H &=& \frac{1}{\pi} \left\{\pi\log{\pi} + \color{red}{\int_{- \infty}^{\infty} \frac{\log{(1+x^2)}}{1+x^2} dx} \right\} \tag{7.1}\\
\\
&=& \frac{1}{\pi} \Bigl\{\pi\log{\pi} + \color{red}{I} \Bigl\} \\
\\
&=& \frac{1}{\pi} \Bigl\{\pi\log{\pi} + \color{red}{2\pi \log 2} \Bigl\} \\
\\
&=& \log \pi + 2\log 2\\
\\
&=& \log 4\pi \tag{7.8}
\end{eqnarray}
ということで、コーシー分布のエントロピーは、 $H=\log 4\pi$ だということが分かりました。
(長かった。。。)
8.Pythonで乱数を発生させてみる。
最後にPythonで乱数を発生させて終わりにしようかなと思います。
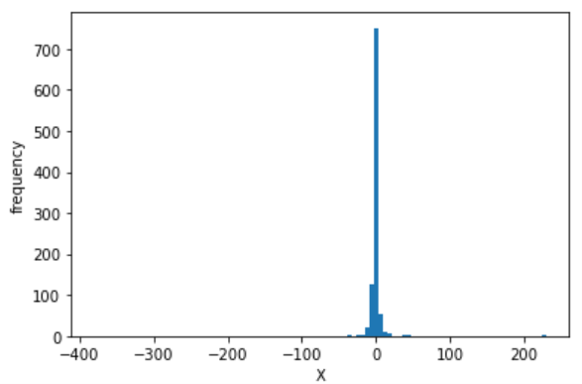
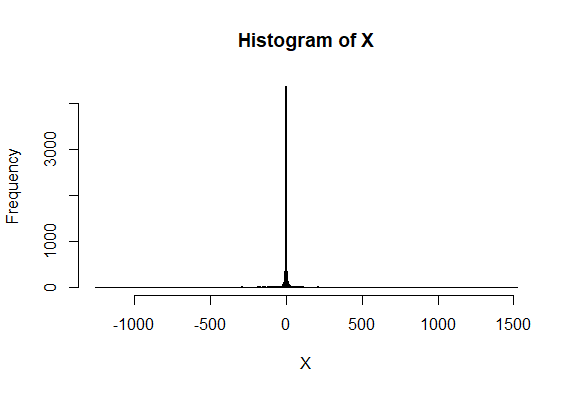
まずは、単純に乱数を1000個発生させて、ヒストグラムを描いてみます。
import numpy as np
import matplotlib.pyplot as plt
X = np.random.standard_cauchy(1000)
plt.hist(X, bins=100)
plt.xlabel("X")
plt.ylabel("frequency")
plt.show()
oh...
すんごいとんがっていますね・・・
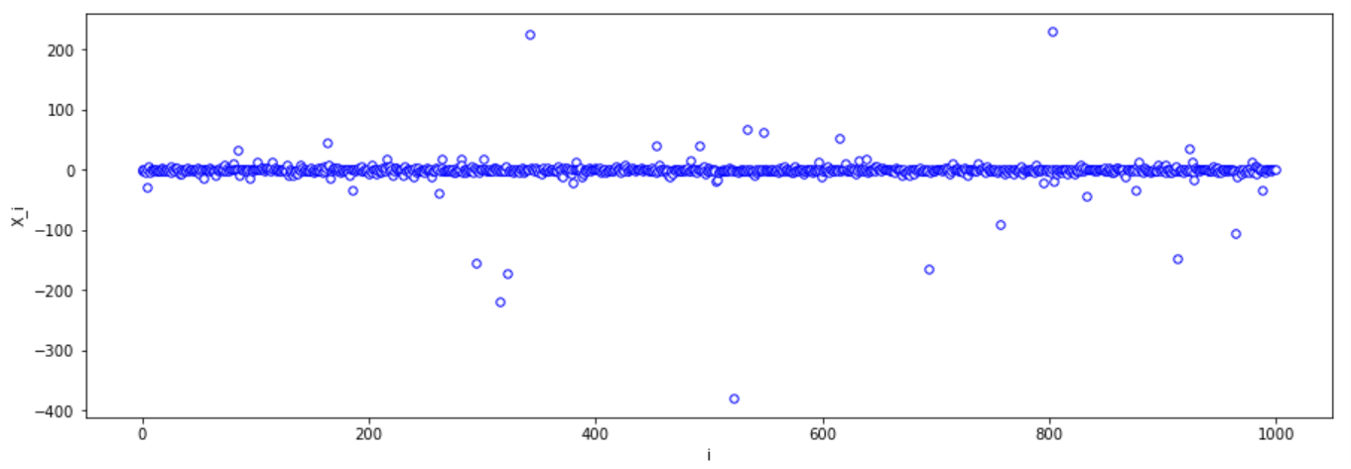
全体を見てみると、
plt.figure(figsize = (15, 5))
plt.scatter(np.arange(1000) ,X, edgecolors="blue", c="white", s=30, marker="o", linewidths=1)
plt.xlabel("i")
plt.ylabel("X_i")
plt.show()
このようになっていて、0から大きく離れた値が少なからず存在していることが分かります。
小さい方から20個取り出してみると、
X1 = np.sort(X)
print(X1[:20])
----- 実行結果 -----
[-380.51927363 -219.50398619 -171.53322282 -163.88009393 -153.45783305
-148.11401422 -104.88118974 -89.13324743 -43.37680232 -38.13581385
-34.29859922 -33.84755224 -33.42707161 -27.9642463 -20.63008814
-20.55987102 -18.43011138 -18.38477693 -16.61787542 -15.28150906]
なので尖がっているのではなく、すごく大きい値をとるものが存在しているために横軸が広がっているだけですね。
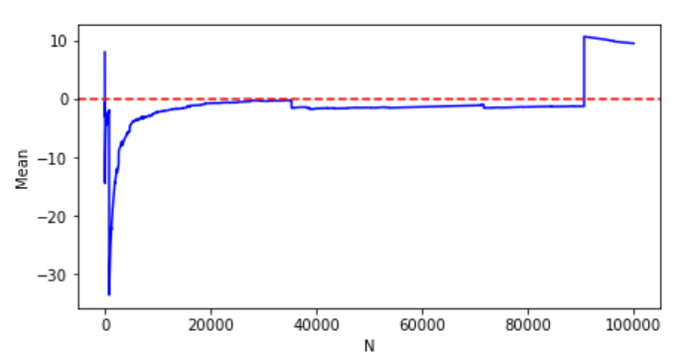
サンプルサイズごとの標本平均の挙動を見てみます。
numpyには、コーシー分布に従う乱数を発生させるものが用意されているので、それを使います。
X_Cauchy = np.random.standard_cauchy(100000)
mu = []
for i in range(len(X_Cauchy)):
mu.append(np.average(X_Cauchy[:i]))
plt.figure(figsize = (7, 3.5))
plt.plot(mu, color = "blue", label = "SampleMean")
plt.axhline(0, ls = "--", color = "red", label = "Median")
plt.xlabel("N")
plt.ylabel("Mean")
なんか、すごく奇妙な動きをしていますね。
恐らくかっくんかっくんしている場所で、極端な数値が観測されているのだと思います。
大数の法則や中心極限定理の前提をそもそも満たしていないので、これらについて考えること自体変なことだと思うのですが、シミュレーションレベルでも無理そうだなということが分かるかと思います。
9.ちなみにRだと
ちなみにRでも、他の確率分布と同じように用意されています。
> X = rcauchy(10000)
> hist(X, breaks="Scott")
使い方は、他の確率分布の時と同じなので、詳しくはみんな大好きこちらのページを見てください。
http://cse.naro.affrc.go.jp/takezawa/r-tips/r/60.html
おしまい
コーシー分布について、ある程度整理できたんじゃないかと思います。
前提知識によって計算の単純さが違ってきたりするっぽく、調べても途中の変形が理解できなかったものが多かったです。
今回この記事で扱っている計算方法は、おそらく最も前提知識がいらない計算方法かなと思います。
数理統計学とか勉強していると「こいつはお前の思い通りにはいかない分布なんだぜ」ぐらいの文脈でしか登場しないため、非常に嫌なイメージがある分布なのですが、ロバスト統計とかで使えそうだな~という漠然とした印象を持ちました。
おしまい。
★参考
[1] 野田,宮岡:数理統計学の基礎(1992)
[2] 藤田:大学生の確率・統計(2010)
[3] 久保川:現代数理統計学の基礎(2017)
[4] 現代数理統計学の基礎サポートページ
URL:https://sites.google.com/site/ktatsuya77/xian-dai
[5] 竹村:現代数理統計学(2020)
[6] 清水:統計学への確率論,その先へ(2019)
[7] MathRelish
URL:https://mathrelish.com/calculation/definite-integral-21
[8] Wikipedia
URL:https://ja.wikipedia.org/wiki/%E3%82%B3%E3%83%BC%E3%82%B7%E3%83%BC%E5%88%86%E5%B8%83