ことのはじまり
僕がいつもどおり楽しくTwitterをしていると科学雑誌のNewtonさんがこんなツイートをしているのを目にしました。
二つの図のうち「ランダムな点の分布」はどちら? こう聞かれて,「左」と答える人もいるでしょう。実際は「右」がランダムな点の分布で,左は点どうしがなるべく重ならないように配置したものです。人は,ランダムである右の図から,“意味がありそうなパターン”を読みとってしまいがちなのです。 pic.twitter.com/tDiheQcUM6
— 科学雑誌Newton(ニュートン)公式 (@Newton_Science) 2018年8月21日
いやいやちょっと待てよと
ランダムという言葉は無作為という意味だけでどういう分布かという意味は含まれていないんだぞ
と思いました。(いや左の図がきれいな数式で決まっているのかもしれませんが…)
Newtonさんの気持ちもわかるんです, 一様分布なんて言葉を使った日には多分わからない人のほうが多いでしょう。
言葉をわかりやすくしたら変になったってことなんだと思います。
でも、これは多分どっちもランダムな要素から生成されています。
ちなみにこのツイートに対して
これなー。自然界で見るのは左側のランダムだからなー。
— ところてん (@tokoroten) 2018年8月22日
右側のランダムは、極めて不自然なんだと思うんよ。
動植物が持つ反応拡散方程式による自己組織化は、どうしても左側のランダムを産んでしまう。
自分の腕を見て、毛の生え方を見れば、左側の分布だ。https://t.co/7FEkMZ0ATf
こういう話もあります。
そこで、いろいろな分布を二次元座標にマッピングして遊ぼうって記事になります。
一応この記事ではランダムという言葉はある分布に従う乱数という意味くらいでふわっと使っています。厳密に確率の定義などをする気はないです。載せている図もコードを簡単にするためや見栄えのための少しラフな方法を用いていることがあります。
方法
ソースコードを見てもらえばわかりますが、
1000px*1000pxの画像を生成してそれをx,yそれぞれ画像の中心を原点として-500~500の範囲にランダムに点を1000個(はみ出るものもあるが気にしない)描画するという方法を取ります。
というわけで早速やってみましょう!
ソースコードはこちらです
https://github.com/Marimoiro/Randomness
一様分布
(x,y)が一様分布
皆さんも知っている一様分布です。


上はC#標準のRandomで下はXorShift(参考)です。
これ以降疑似乱数はすべてxorshiftを使用します。
Newtonさんの言う通りところどころ団子状になったものが見受けられますね!
(r,θ)が一様分布
こちらはx,yではなくr(距離)とθ(角度)を一様分布で決定してみました。
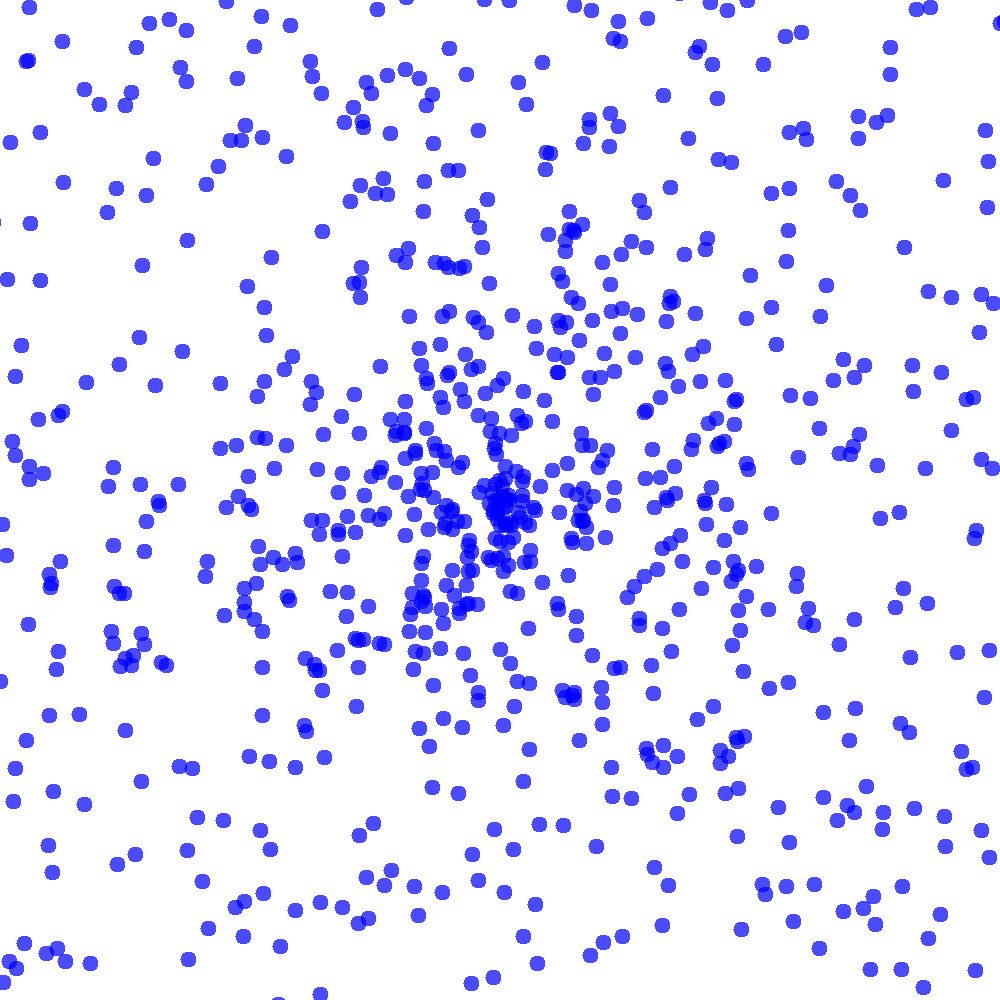
中心に近ければ近いほど密度が当然高くなっていることがわかりますね!
中心に偏ってるけどランダムから作りましたよ!!
点が周辺抑制効果を持つモデル
Newtonさんがランダムではないって言ったやつっぽい画像を作ってみました。
点が周辺抑制効果を持つモデル
次のようなモデルを考えました。
まず画像を格子状に分割します。その格子一つ一つに0ポイントで初期化します。
そして最初の一つの点は(x,y)の一様分布で決定します。
画像の白い部分が決定された点が含まれる格子点だとすると、白は3ポイント,青は2ポイント,赤は1ポイント
(斜めはめんどくさかったのでなし)
を追加します。
次の格子点の候補を(x,y)の一様分布で決定します。この候補は0ポイントを持っています。
格子(x,y)が持っているポイントよりも高ければ正式な次の格子点となることができます。そして1つ目と同様にポイントを振ります。
さてなれなかった場合ですが格子点候補をもう一度決め直します。ただし格子点のポイントは+1します。
これを格子点が決まるまで繰り返します。
これはすでにある点は他の点が周囲に出現するのを抑制する効果を持っているモデルになります。
ちなみに植物学用語でこういう相互作用をアレロパシーって言うらしいです。(相互作用という意味だけで抑制効果の意味はないそうです。)
確かに…点どうしの重なりが少ない…気が…する?
もう少しはっきりとNewtonさんの図に近づけるモデルにしましょう。
強力な周辺抑制効果
今度は同じ要領で点を打ちますが周辺に点を打たれるのを抑制する効果を超強力にしました。
自分の周辺の5*5の25マスに100ポイントを与えることにします。
今回は100回で諦めて一様分布に切り替えることにしたのでほぼ周りに点が出現できなくなります。(101回目は一様分布なので出現する可能性があります。)
そういう感じで作った画像がこちら

いい感じにほぼ重なりがなくなったんじゃないでしょうか?
ただしこれも乱数から作られるランダムです。(もちろんこれは状態を持った確率分布に従うランダムです)
一様分布以外の確率分布
一様分布以外も二次元にプロットしてみましょう。
指数分布
指数分布を二回とってそれぞれ(x,y)に対応させています。
左上が(0,0)にしたので左上に寄っていますね。

参考として逆関数法を用いた乱数生成の証明と例
多項分布
今回はそれぞれ確率xは0.5,yは0.3で成功する試行を50回やったときの成功回数の分布になります。
これは同じ値がたくさん出てくるので点にアルファ値を設定しています。色が濃いほどたくさん出ていることになります。
特殊なランダムさ
ちょっとおもしろいものをいくつか紹介します
格子が固さをもつようなモデル
今回のモデルも格子で考えます。
前は点を打つとその周辺にポイントを振っていましたが、今回は格子に最初にポイントをランダムに振ります。
最初に1つ原点に格子点を置きます。次の点は前の点の周辺の格子点の中で一番ポイントの高い格子点になります。
次はこの2つの格子点の周辺で一番ポイントの高いもの…
次はこの3つの格子点の周辺で一番ポイントの高いもの…
として1000個点を決めます。
そうすると次のような図になります。

見てみると中心にまとまっていますがところどころスカスカな部分があります。
これは例えば土のに水が染み込んでいくときの挙動に似ています。
点が打たれているところは水が染み込んで行った部分
中心部にあるのに白い部分は小石などで水が流れられなかった部分に相当します。
というわけでこのモデルはパーコレーションモデルと言うそうです。
赤が最初で緑が最後のほうで加わった点になっています。
ランダムウォーク
まず点を一つ(0,0)に置きます。
おいた点はその周囲をランダム(分布は適当に)に少しだけ移動します。
これを繰り返したときの点の軌跡を記録したものです。
赤がスタートで緑がゴールになっています。
ランダムウォーク自体も楽しい性質がありますが、割愛します。
DLAクラスタ
最後にランダムウォークを利用したDLAクラスタというものを紹介します。
作り方はこうです。
原点に一つ点を置きます。(以後クラスタと呼びます)
このクラスタの周辺にランダムに点を起きます。この点はランダムウォークをします。
点がクラスタの近くにくると点はクラスタと合体してその場に留まります。
離れすぎると消滅します。
これを繰り返してどんどんと点を合体させていくと次のような図になります。
これの特徴としては中心部分にはほとんど最後の方で追加された緑の点は付着できていないように見えることです。
基本的にはランダムウォークは上の図を見ると分かる通り横幅が大きくなる傾向にあります。
なので内部に付く前に周りの枝にくっついちゃうんですね。
ちなみにこの形は金属葉と呼ばれるものと近くなります。
雷なんかも似たような原理で形の説明ができるようです。
まとめ
以上いろんなランダムから作られる2次元画像でした!





