2次元正規分布でギブスサンプリングする【Python】

はじめに

ギブスサンプリングに関する備忘録です。(「続・わかりやすいパターン認識―教師なし学習入門」の付録に載ってあります)
どこかに間違いがあるでしょう(断言)

ギブスサンプリングについて

ギブスサンプリング(Gibbs Sampling)は、直接サンプルを得ることが難しい高次元の同時分布の条件付き分布が計算できるときに、サンプルを生成することができるマルコフ連鎖モンテカルロ法(Markov Chain Monte Carlo methods, MCMC)のひとつです。

$N$個の確率変数からなる分布を考えると、ある確率変数以外が与えられた時の条件付き分布を考えて、その確率変数の実現値を発生させていき、これをすべての確率変数1つ1つに適用していくことで、マルコフ性を持つ(特定の座標方向で移動量が確率的に決まる)サンプル列を生成することができます。俗に言う「カクカク」動くというのは、ここに起因しています。

生成サンプル列は積分近似などに利用されます。例えば、ベイズ主義では周辺尤度(ベイズの定理:式(1)の分母)を計算する際に変数の数だけ多重積分をする必要があります。この積分の計算は困難なので、MCMCで拾ってきたサンプルの和に近似的に置き換えることが行われたりします。また、制約ボルツマンマシン(Restricted Boltzmann Machine, RBM)の学習にもMCMC(ギブスサンプリングが採用されています。詳しくは青イルカ本で)が用いられるようです。

ベイズの定理

観測データ$\boldsymbol{x}=\begin{pmatrix}x_1 & \cdots & x_n \end{pmatrix}$と分布パラメータ$\boldsymbol{w}=\begin{pmatrix}w_1 & \cdots & w_m \end{pmatrix}$があるとすると、$\boldsymbol{w}$に関する事後分布$p(\boldsymbol{w} \mid \boldsymbol{x})$は、事前に用意した$\boldsymbol{w}$に関する分布$p(\boldsymbol{w})$と分布に対するデータ\boldsymbol{x}の尤度$p(\boldsymbol{x} \mid \boldsymbol{w})$から計算できて式(1)のように表されます。

\begin{align}
p(\boldsymbol{w} \mid \boldsymbol{x}) &= \frac{p(\boldsymbol{x} \mid \boldsymbol{w})p(\boldsymbol{w})}{p(\boldsymbol{x})}\\
&= \frac{p(\boldsymbol{x} \mid \boldsymbol{w})p(\boldsymbol{w})}{\int_\boldsymbol{w}p(\boldsymbol{x} \mid \boldsymbol{w})p(\boldsymbol{w})d\boldsymbol{w}} \tag{1}
\end{align}

多次元正規分布

言わずもがな有名な分布ですが一応。各要素が正規分布に従う$N$次元の観測データ$\boldsymbol{x}$の同時分布は平均ベクトル$\boldsymbol{\mu}$と共分散行列$\Sigma$を用いて式(2)で表されます。

p(\boldsymbol{x}) = \frac{1}{(2\pi)^{\frac{N}{2}}\left|\Sigma\right|^{\frac{1}{2}}} \exp \left( -\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T \Sigma^{-1} (\boldsymbol{x}-\boldsymbol{\mu}) \right) \tag{2} 

2次元正規分布と条件付き分布

2次元正規分布を「続・わかりやすいパターン認識―教師なし学習入門」に従って、式(2)と式(3)の平均ベクトルと式(4)の共分散行列(の逆行列)によって規定します。ただし、$-1<a<1$です。

\boldsymbol{\mu}=\boldsymbol{0} \tag{3}

\Sigma^{-1}=\left(
\begin{matrix} 
1 & -a \\
-a & 1 
\end{matrix} 
\right) \tag{4}

$\boldsymbol{x}=(x_1, x_2)$として式(2)をスカラー表記に書き下すと式(5)になります。便宜のため、指数部は$x_1$で平方完成した形に変形しています。

\begin{align}
p(x_1, x_2) &= \frac{\sqrt{1-a^2}}{2\pi} \exp \left(-\frac{1}{2}(x_1^2-2ax_1x_2+x_2^2)\right) \\
&= \frac{\sqrt{1-a^2}}{2\pi} \exp \left(-\frac{1}{2}(1-a^2)x_2^2\right)  \exp \left(-\frac{1}{2}(x_1-ax_2)^2\right) \tag{5}
\end{align}

次に条件付き分布$p(x_1 \mid x_2)$を考えます。これは定義と周辺化によって式(6)のように表されます。

p(x_1 \mid x_2) = \frac{p(x_1, x_2)}{p(x_2)} = \frac{p(x_1, x_2)}{\int_{-\infty}^{\infty}p(x_1, x_2)dx_1} \tag{6}

式(6)の周辺化するための積分は当然ですが$x_1$に関するガウス積分になっているので、結局$p(x_1 \mid x_2)$は式(7)のように計算できます。(ガウス積分はそれ自身を2乗をした後、極座標変換をすることで簡単に計算できます)

\begin{align}
p(x_1 \mid x_2) &= \frac{p(x_1, x_2)}{\int_{-\infty}^{\infty}p(x_1, x_2)dx_1} \\
&= \frac{\frac{\sqrt{1-a^2}}{2\pi} \exp \left(-\frac{1}{2}(1-a^2)x_2^2\right)  \exp \left(-\frac{1}{2}(x_1-ax_2)^2\right)}{\frac{\sqrt{1-a^2}}{\sqrt{2\pi}} \exp \left(-\frac{1}{2}(1-a^2)x_2^2\right)} \\
&= \frac{1}{\sqrt{2\pi}} \exp \left(-\frac{1}{2}(x_1-ax_2)^2\right) \tag{7}
\end{align}

また、式(5)の対称性より式(7)の$x_1$と$x_2$を入れ替えても問題ないので、$p(x_2 \mid x_1)$はただちに式(8)のように計算できます。

p(x_2 \mid x_1) =  \frac{1}{\sqrt{2\pi}} \exp \left(-\frac{1}{2}(x_2-ax_1)^2\right) \tag{8}

ギブスサンプリングの実装

このようにして、すべての条件付き分布を計算することができました。データの分布が2次元正規分布の場合のギブスサンプリングは、これらの条件付き分布に対して以下に示すように行われます。これをプログラムで実装すると当初の目的を達成できます。

1. $x_1$、$x_2$の初期化
2. 与えられた$x_2$で$p(x_1 \mid x_2)$に基づいて$x_1$を発生させる
3. $x_1$を置き換えて値を更新
4. 与えられた$x_1$で$p(x_2 \mid x_1)$に基づいて$x_2$を発生させる
5. $x_2$を置き換えて値を更新
6. 2.〜5.を繰り返す

このようにして生成したサンプル列のうち、初期値に近いものは分布から得たものとは言い難く、バーンイン(burn-in)期間を設定して破棄しなければいけません。さらに、マルコフ性を基にしたサンプリング方法であるが故に、独立同分布(independent and identically distributed, i.i.d.)なサンプルが欲しい時は、すべてのサンプルを使用することは避けるべきです。2つのサンプルの間を空けて、また間のサンプルを破棄しなければなりません。(今回のプログラムでは破棄していませんのでご注意ください)

このアルゴリズムをPythonで実装してみました。正規分布の計算は通常ScipyでできますがPythonista3には無かったので、自分で書いています。
gaussian関数の処理について、np.meshgridでメッシュを生成した後に、このまま正規分布を計算します。その後、対角成分のみを取得することで入力メッシュの出力を得ることができます。

# sampling from multivariate gaussian distribution using gibbs sampling

import numpy as np
import matplotlib.pyplot as plt
import math

# Calculate multivariate gaussian distribution
# x, y : do np.meshgrid
def gaussian(x, y, mean, co_var):
    output = np.array([])
    x = x - mean[0]
    y = y - mean[1]
    for i in range(x.shape[0]):
        z = 1/(2*math.pi)*math.sqrt(np.linalg.det(co_var))*np.exp(-0.5 * np.dot(np.dot(np.array([x[i, :],y[i, :]]).T, np.linalg.inv(co_var)), np.array([x[i, :],y[i, :]])))
        z = np.diag(z)
        output = np.append(output, z)
    output = output.reshape(x.shape[0], x.shape[0])
    return output

# initialize
x = np.array([5., -5.])
# a : -1<a<1
a = 0.5
step = 1000
sample = np.array(x)

# gibbs sampler
for i in range (step):
    x[0] = np.random.normal(a*x[1], 1)
    sample = np.append(sample, (x))
    x[1] = np.random.normal(a*x[0], 1)
    sample = np.append(sample, (x))

sample = sample.reshape((2*step+1, x.shape[0]))

# drawing multivariate gaussian distribution
t = np.arange(-5, 5, 0.1)
x,y =np.meshgrid(t, t)
z = gaussian(x, y, np.array([0, 0]), 1/(1-a**2) * np.array([[1, a],[a, 1]]))

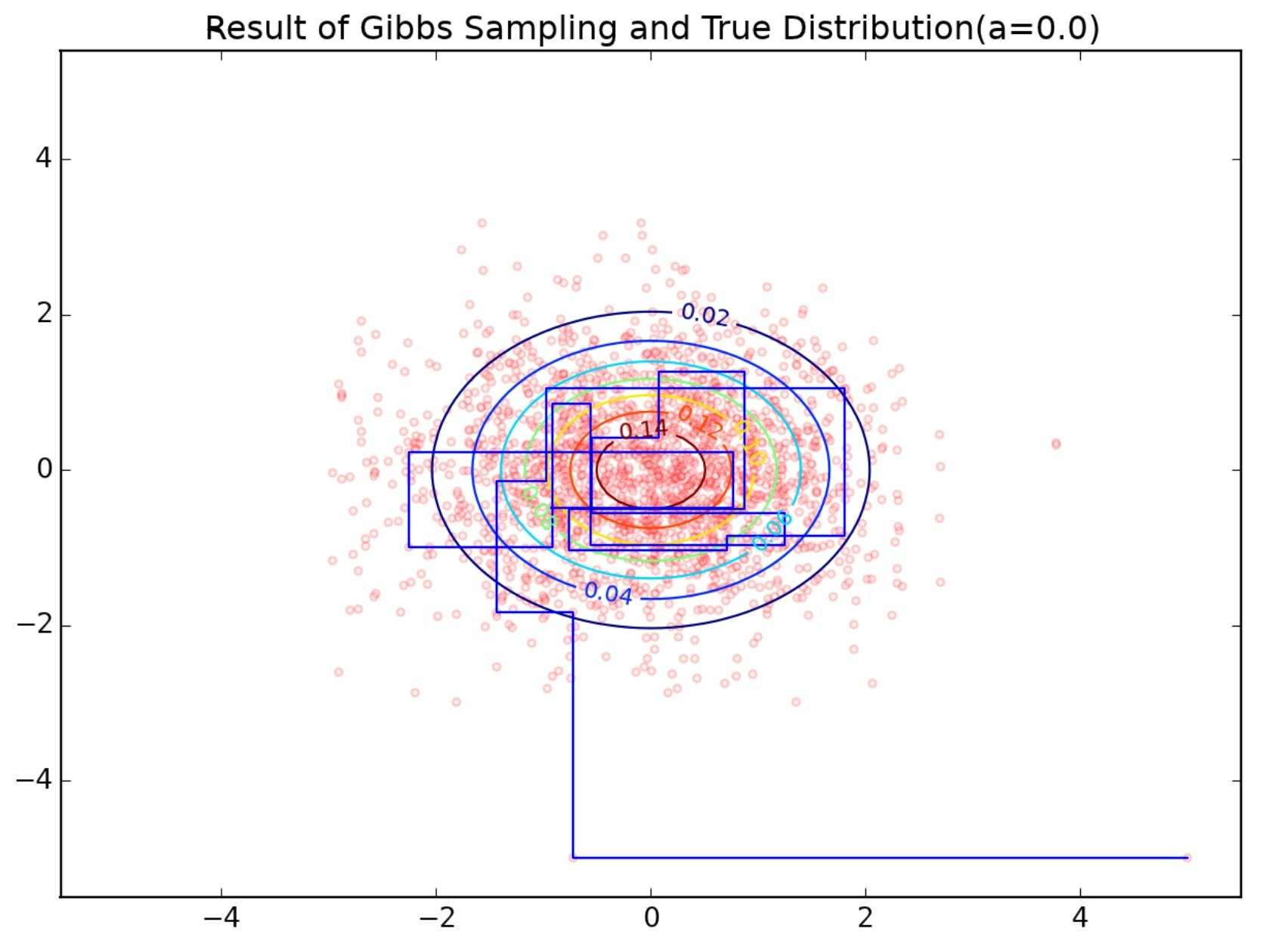
plt.title('Result of Gibbs Sampling and True Distribution(a={})'.format(a))
plt.scatter(sample[:, 0], sample[:, 1], s=10, c='pink', alpha=0.2, edgecolor='red')
# Tracking Gibbs Sampling
plt.plot(sample[0:30, 0], sample[0:30, 1])

c = plt.contour(x,y,z)
c.clabel(fmt='%1.2f', fontsize=10)
plt.show()

ギブスサンプリングの結果

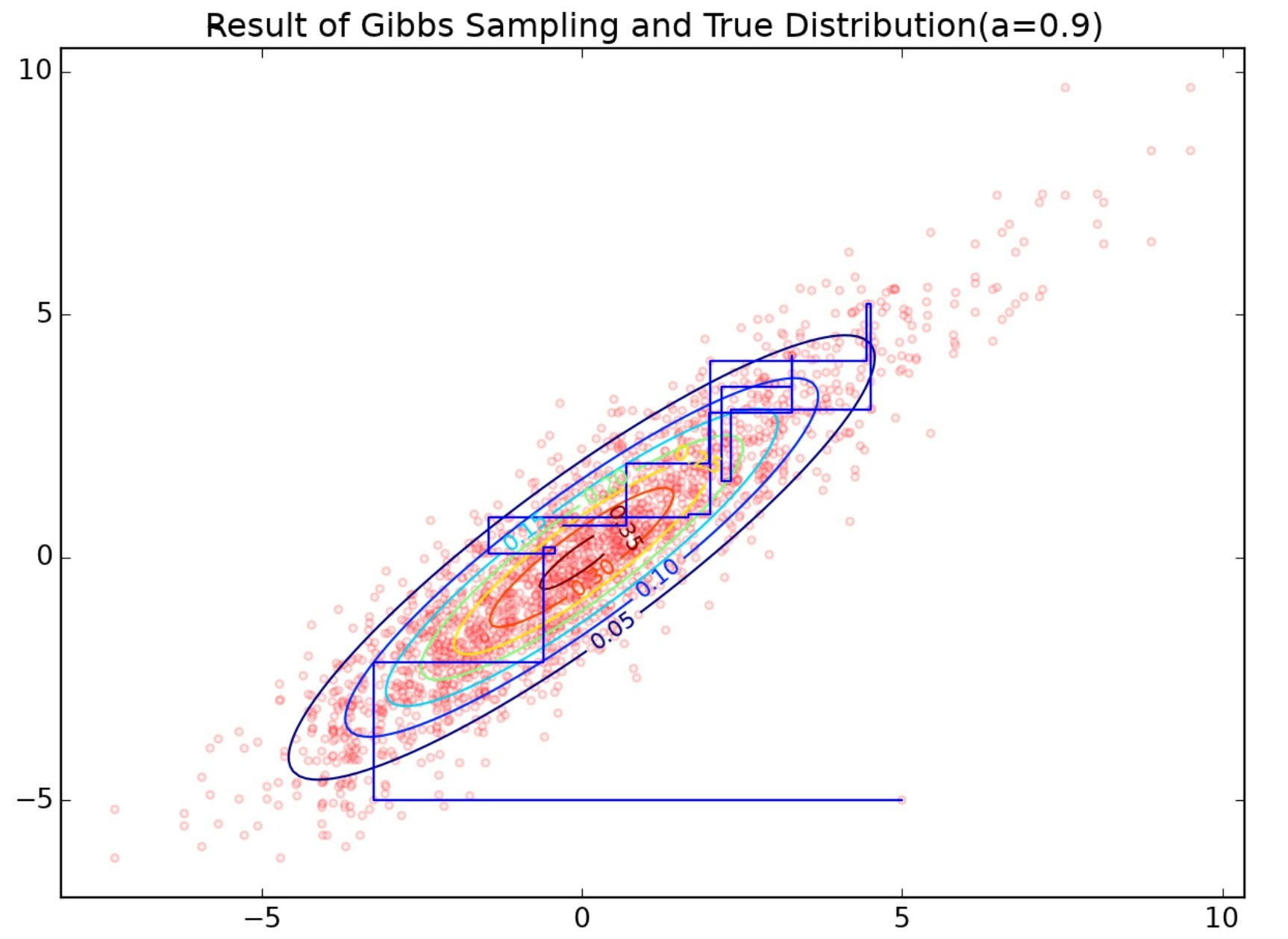
上のプログラムの結果が下図です。$a=0.5$のときは分布から綺麗にサンプリングできていることがわかります。$a=0.9$のときはサンプリングがやや短軸方向を重点的にサンプリングされてしまっています。何ででしょうね(すっとぼけ)。
2019/6/1追記:
x[0] = np.random.normal(a*x[1], 1)とx[1] = np.random.normal(a*x[1], 1)で1/sqrt(2*math.pi)を誤って乗算していたことが間違っていたようです。ご指摘ありがとうございます。

$a=0.9$の時のサンプリング結果を見ると、分布の等高線より右上側にサンプル多くあることがわかりますが、これは2つのサンプル間に破棄期間を設けなかったために、マルコフ性が作用して外側にサンプルが分布の外側を遷移し続けた状況と考えられます。

ギブスサンプリングを始めて30ステップの軌跡を青線で追っています。冒頭述べた通り「カクカク」動いているのが見てわかります。

まとめ/予定

ギブスサンプリングによって2次元正規分布からサンプル列を得ました。今後の予定としては、このサンプル列を用いて、最尤推定/MAP推定/ベイズ推定を行なって真の分布と比較したいと思います。