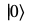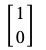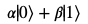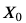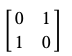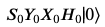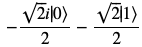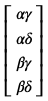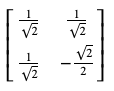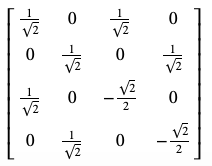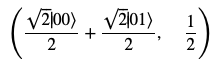#はじめに
はじめまして。株式会社Qunasys(https://qunasys.com) インターンの中井と申します。
今シリーズでは、弊社が開発した量子コンピューティングの教材Quantum Native Dojo の詳しい解説をしていきます。まだ部分的にしか公開されていないので、新しい記事が公開され次第、解説を書いていきます。
#Quantum Native Dojoの使い方
https://github.com/qulacs/quantum-native-dojo のREADME.mdを参照して下さい。
ちなみに、今回の記事は主に「第1章 量子情報理論入門 1-1.量子情報の基礎」
(https://github.com/qulacs/quantum-native-dojo/blob/master/notebooks/1.1_basics_of_quantum_information.ipynb) の内容を分かりやすくしています。
##量子コンピュータとは
最近、量子コンピュータという単語を耳にすることが多くなりました。ではなぜ量子コンピュータとはそもそも何なのでしょうか？
量子コンピュータは、量子力学の原理を用いて演算を行うコンピュータです。量子ゲート型コンピュータ(量子コンピュータの国際的な定義)です。これは既存のコンピュータ同様、ゲート操作により様々な計算をするコンピュータです。ちなみに、このゲート操作は量子ゲート(後述)という、全く違うゲート操作です。
量子コンピュータの詳しい動作原理を理解するには、量子力学と量子計算理論（量子系で計算をするための理論)を知っておく必要があります。
##なぜ注目されているのか
量子コンピュータの開発が期待されているのは、既存のコンピュータで(現実的な時間に)解けない問題の計算時間を短縮できることがあるからです。
既存のコンピュータでは計算に時間がかかりすぎる問題の代表例に、素因数分解や量子化学の問題が挙げられます。既存のコンピュータ上の最良のアルゴリズムでも、入力数に対して指数関数的に多い処理回数が必要ですが、量子コンピュータで要求される処理回数は入力に対して多項式レベルです。これは素因数分解を解くときに、既存のコンピュータでは選択肢を１つ１つ試さなければいけないのに対し、量子コンピュータでは全ての量子ビットで重ね合わせ状態を生成し、欲しい解を得る確率を増幅させることで時間の短縮を図っています。[1]
また、今クラウド上で利用されている量子コンピュータは演算に伴うエラーが多いので、既存のコンピュータと量子コンピュータの合わせ技が考えられています。これは、量子計算が必要な過程のみ量子コンピュータを用いるアルゴリズムで、既に量子化学など既存のコンピュータで不可能な計算が、可能になると期待されています。
ではQuantum Native Dojoで一緒に勉強していきましょう。
#量子ビットとは
量子ビットの0と1は以下の行列と対応します。[2]
|0\rangle = \left(
\begin{array}{r}
1\\
0 \\
\end{array}
\right)
\,,\,
|1\rangle = \left(
\begin{array}{r}
0\\
1 \\
\end{array}
\right)
物理的には|0>はエネルギーが低い状態、|1>はエネルギーが高い状態で、|0>から|1>にするにはエネルギー差に相当するエネルギーを持つ電磁波を照射する等の方法があります。
量子ビット |ψ>は以下のように表されます。
|\psi\rangle = \alpha|0\rangle + \beta|1\rangle
量子力学では、量子は２つの状態を取っていますが、状態を観測するとどちらかの状態に収束することが知られています。
この場合、|0>が得られる確率が|α|^2、|1>が得られる確率が|β|^2です。
例えば
|\psi\rangle = \frac{1}{\sqrt{2}}|0\rangle + \frac{1}{\sqrt{2}}|1\rangle
は|0>,|1>を得る確率がそれぞれ50%である状態と言えます。((1/√2)^2 = 1/2より)
次は、これをPythonライブラリのSympyを使って実装していきます。
#必要なライブラリをインポートする
from IPython.display import Image, display_png
from sympy import *
from sympy.physics.quantum import *
from sympy.physics.quantum.qubit import Qubit,QubitBra
init_printing() # ベクトルや行列を綺麗に表示するため
psi = Qubit('0')
psi #ブラケット表示
すると、
と表示される。
また、
represent(psi) #列ベクトル表示
を実行すると、
と表示されます。
また、
|\psi\rangle = \alpha|0\rangle + \beta|1\rangle
のように係数を文字にしたければ、
a, b = symbols('alpha, beta') #a, bをシンボルとして、alpha, betaとして表示
ket0 = Qubit('0')
ket1 = Qubit('1')
psi = a * ket0 + b* ket1
psi # 状態をそのまま書くとケットで表示してくれる
を実行すれば
が得られます。
勿論、係数を数にする事も出来ます。例えば、
psi.subs([([a,1/sqrt(2)]),([b,1/sqrt(2)])]) # alpha, betaに具体的な数字を代入
を実行すれば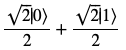
と、先ほど紹介した重ね合わせ状態を生成できます。
#ブラケット記法
量子ビットを始め、今後量子コンピューティングの勉強をしていくと、|α>のような表記を目にする思います。このような書き方をブラケット記法と言います。ブラケットは英語で括弧の意味で<|はブラ、|>はケットと呼ばれています。
仮に異なる状態を取る量子ビット
|\psi\rangle = \left(
\begin{array}{r}
\alpha\\
\beta \\
\end{array}
\right)
\, , \,
|\phi\rangle = \left(
\begin{array}{r}
\gamma\\
\delta \\
\end{array}
\right)
```py
があるとすると、
```math
\langle\psi|\phi\rangle
= \left(
\begin{array}{rr}
\alpha^{\ast} & \beta^{\ast} \\
\end{array}
\right)
\left(
\begin{array}{rr}
\gamma \\
\delta \\
\end{array}
\right)
= \alpha^{\ast}\gamma + \beta^{\ast}\delta
より、内積が取れる。
かける順番を逆にすると、
|\phi\rangle\langle\psi |
= \left(
\begin{array}{rr}
\gamma \\
\delta \\
\end{array}
\right)
\left(
\begin{array}{rr}
\alpha^{\ast} & \beta^{\ast} \\
\end{array}
\right)
= \left(
\begin{array}{rr}
\gamma\alpha^{\ast} & \gamma\beta^{\ast} \\
\delta\alpha^{\ast} & \delta\beta^{\ast} \\
\end{array}
\right)
のように演算子が作れる。
#量子ビットに対する基本演算
測定を除く量子演算の最大の特徴は以下の２つです。
1.線形性
2.ユニタリー性
###線型性とは
演算fが以下の２つの条件を満たせば、fが線形であると言えます。
\ \ \ (i) \,f(x+y) = f(x) + f(y)
(ii) \, f(ax) = af(x)
量子演算でいうと、量子状態|ψ>,|φ>を重ね合わせた状態|ψ>+|φ> に 量子演算Uをかけたら、
演算結果が両方の状態に操作Uをした状態の重ね合わせU(|ψ>+|φ>) = U|ψ> + U|φ>になるということだ。
ユニタリー性とは
行列Uと、Uの転置行列の複素共役であるU†が
U^{\dagger} U = I
を満たす時、Uはユニタリー行列であるといいます。
1量子ビットに作用する量子ゲートのうち、代表的なものの集まりはパウリ演算子と呼ばれるもので、以下の４つが挙げられます。
I = \left(
\begin{array}{r}
1 & 0\\
0 & 1\\
\end{array}
\right)
\,,\,
X = \left(
\begin{array}{r}
0 & 1\\
1 & 0\\
\end{array}
\right)
\,,\,
Y = \left(
\begin{array}{r}
0 & - i\\
i & 0\\
\end{array}
\right)
\,,\,
Z = \left(
\begin{array}{r}
1 & 0\\
0 & -1\\
\end{array}
\right)
\,,\,
H = \left(
\begin{array}{r}
1 & 1\\
1 & -1\\
\end{array}
\right)
また、これらのうち、Hゲート以外は全てパウリ演算子と呼ばれる行列です。
次に各ゲートの説明をしていきます。
- Iゲート
Iゲートは状態を変化させないゲートです。
I|0\rangle = \left(
\begin{array}{r}
1 & 0\\
0 & 1\\
\end{array}
\right)
\left(
\begin{array}{r}
1\\
0 \\
\end{array}
\right)
= \left(
\begin{array}{r}
1\\
0 \\
\end{array}
\right)
= |0\rangle\\
I|1\rangle = \left(
\begin{array}{r}
1 & 0\\
0 & 1\\
\end{array}
\right)
\left(
\begin{array}{r}
0\\
1 \\
\end{array}
\right)
= \left(
\begin{array}{r}
0\\
1\\
\end{array}
\right)
= |1\rangle
- Xゲート
Xゲートは量子ビットの値を反転させる役割があります。
X|0\rangle = \left(
\begin{array}{r}
0 & 1\\
1 & 0\\
\end{array}
\right)
\left(
\begin{array}{r}
1\\
0 \\
\end{array}
\right)
= \left(
\begin{array}{r}
0\\
1 \\
\end{array}
\right)
= |1\rangle\\
X|1\rangle = \left(
\begin{array}{r}
0 & 1\\
1 & 0\\
\end{array}
\right)
\left(
\begin{array}{r}
0\\
1 \\
\end{array}
\right)
= \left(
\begin{array}{r}
1\\
0 \\
\end{array}
\right)
= |0\rangle
3.Zゲート
Zゲートは、|1>の位相を反転させる役割があります。
Z|0\rangle = \left(
\begin{array}{r}
1 & 0\\
0 & -1\\
\end{array}
\right)
\left(
\begin{array}{r}
1\\
0 \\
\end{array}
\right)
= \left(
\begin{array}{r}
1\\
0 \\
\end{array}
\right)
=|0\rangle\\
Z|1\rangle = \left(
\begin{array}{r}
1 & 0\\
0 & -1\\
\end{array}
\right)
\left(
\begin{array}{r}
0\\
1 \\
\end{array}
\right)
= \left(
\begin{array}{r}
0\\
-1 \\
\end{array}
\right)
= -|1\rangle
4.Yゲート
Y = \left(
\begin{array}{r}
0 & - i\\
i & 0\\
\end{array}
\right)
= i \left(
\begin{array}{r}
0 & 1\\
1 & 0\\
\end{array}
\right)
\left(
\begin{array}{r}
1 & 0\\
0 & -1\\
\end{array}
\right)
= iXZ
より、XゲートとZゲートを1度にかけたようなゲートです。
4.Hゲート
Hゲートこそ、重ね合わせ状態を生成するために必要なゲートです。
H|0\rangle
= \frac{1}{\sqrt{2}}
\left(
\begin{array}{rr}
1 & 1\\
1 & -1\\
\end{array}
\right)
\left(
\begin{array}{r}
1 \\
0 \\
\end{array}
\right)
=\frac{1}{\sqrt{2}}
\left(
\begin{array}{r}
1 \\
1 \\
\end{array}
\right)
= \frac{1}{\sqrt{2}}
\left(
\begin{array}{r}
1 \\
0 \\
\end{array}
\right)
+\frac{1}{\sqrt{2}}
\left(
\begin{array}{r}
0 \\
1 \\
\end{array}
\right)
= \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\\
H|1\rangle
= \frac{1}{\sqrt{2}}
\left(
\begin{array}{rr}
1 & 1\\
1 & -1\\
\end{array}
\right)
\left(
\begin{array}{r}
0 \\
1 \\
\end{array}
\right)
=\frac{1}{\sqrt{2}}
\left(
\begin{array}{r}
1 \\
-1 \\
\end{array}
\right)
= \frac{1}{\sqrt{2}}
\left(
\begin{array}{r}
1 \\
0 \\
\end{array}
\right)
-\frac{1}{\sqrt{2}}
\left(
\begin{array}{r}
0 \\
1 \\
\end{array}
\right)
= \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)
Sympyを用いた1量子ビットゲートの演算
では、先ほど同様Sympyを用いた計算をしていきましょう。
#必要なライブラリをインポート
from sympy.physics.quantum.gate import X,Y,Z,H,S,T,CNOT,SWAP, CPHASE
X(0) #量子ビットを1個用意し、それにXゲートをかけます。
これを実行すると
が得られます。
represent(X(0),nqubits=1) # パウリX
を入力すると
と、行列の形で出力されます。
ketを用いて記述する事も出来ます。
S(0)*Y(0)*X(0)*H(0)*ket0
すると、
が得られます。
また、qapplyを用いると実際に量子ビットに量子ゲートをかけることが出来ます。
qapply(S(0)*Y(0)*X(0)*H(0)*ket0)
すると、
と、演算後の状態が出力されます。
##複数量子ビットに対する演算
次に、複数の量子ビットの状態の変化について考えてみましょう。ここでは簡易性のため2量子ビットの状態を扱います。
|\psi\rangle = c_{00}|00\rangle+c_{01}|01\rangle+c_{10}|10\rangle +c_{11}|11\rangle\\
(c_{xx} \,means\,the\,probability
\,of\,getting\,the\,state\,|xx\rangle)
という状態の2量子ビットがあった時、
|\psi\rangle = \left(
\begin{array}{r}
c_{00} \\
c_{01} \\
c_{10} \\
c_{11} \\
\end{array}
\right)
と１つの行列でも表すことができます。また、1桁目の量子状態|q0>、2桁目の量子状態|q1>が
|q_0\rangle = \alpha|0\rangle + \beta|1\rangle \\
|q_1\rangle = \gamma|0\rangle + \delta|1\rangle
だった時、
これは行列で
|\psi\rangle = \left(
\begin{array}{r}
\alpha \gamma \\
\alpha \delta \\
\beta \gamma \\
\beta \delta \\
\end{array}
\right)
と表現できます。
また、量子状態を表すもう１つの表現方法として、以下のようなものもあります。
|\psi\rangle = (\alpha|0\rangle + (\beta|1\rangle) \otimes (\gamma|0\rangle + \delta|1\rangle)
ちなみに、これはテンソル積 といいます。
##複数量子ゲート
先ほど紹介したのは1量子ビットに作用するゲートでしたが、複数の量子ビットにまたがって作用する量子ゲートも存在します。その代表例が制御NOT(CNOT)ゲートです。これは2量子ゲートで、片方の量子ビット(制御ビット)の値が1の時、もう片方の量子ビット(標的ビット)の値を反転させるゲートです。これは以下のように１つの行列で表せます。
CNOT = \left(
\begin{array}{rrrr}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
\end{array}
\right)
#Qubitの並び順は右から左
qapply(CNOT(0,1)*Qubit('01'))
のコードを実行すると、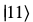
が得られる。これは制御ビット(Qubitの右の方)が1なので、標的ビット(Qubitの左の方)の0から1に変わるからです。
##Sympyを用いたテンソル積の計算
a,b,c,d = symbols('alpha,beta,gamma,delta')
psi = a*Qubit('0')+b*Qubit('1')
phi = c*Qubit('0')+d*Qubit('1')
TensorProduct(psi, phi) #テンソル積
を実行すると、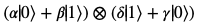
が得られます。ちなみに、行列形にしたければお気付きの通り
represent(TensorProduct(psi, phi))
とすれば
と出力されます。
演算子のテンソル積
何番目のビットに何ゲートをかけるかというのも、テンソル積で表すことが出来ます。
例えば、２つの演算子A,Bが
A = \left(
\begin{array}{rr}
a_{11} & a_{12}\\
a_{21} & a_{22}\\
\end{array}
\right)
\,,\,
B=\left(
\begin{array}{rr}
b_{11} & b_{12}\\
b_{21} & b_{22}\\
\end{array}
\right)
と表される時、Aを1番目の量子ビットに、Bを2番目の量子ビットにかける時、量子ビット群全体にかける量子ゲートは、以下のようなテンソル積で表せます。
A \otimes B = \left(
\begin{array}{rr}
a_{11} & a_{12}\\
a_{21} & a_{22}\\
\end{array}
\right)
\left(
\begin{array}{rr}
b_{11} & b_{12}\\
b_{21} & b_{22}\\
\end{array}
\right)
= \left(
\begin{array}{rrrr}
a_{11}b_{11} & a_{11}b_{12} & a_{12}b_{11} & a_{12}b_{12} \\
a_{11}b_{21} & a_{11}b_{22} & a_{12}b_{21} & a_{12}b_{22} \\
a_{21}b_{11} & a_{21}b_{12} & a_{22}b_{11} & a_{22}b_{12} \\
a_{21}b_{21} & a_{21}b_{22} & a_{22}b_{21} & a_{22}b_{22}\\
\end{array}
\right)
これを例のごとくSympyで実装してみましょう。
represent(H(0),nqubits=1)
を実行すると
、つまり1量子ビットのHゲートが得られます。
次に、2量子ビットのうち1番目だけにHゲートをかける場合を考える。つまり以下のコードを実行すると、
represent(H(1),nqubits=2)
が得られます。
これは
H \otimes I = \frac{1}{\sqrt{2}}
\left[
\begin{array}{rr}
1 & 1\\
1 & -1\\
\end{array}
\right]
\otimes
\left[
\begin{array}{rr}
1 & 0\\
0 & 1\\
\end{array}
\right]
= \frac{1}{\sqrt{2}}\left[
\begin{array}{rrrr}
1 & 0 & 1 & 0 \\
0 & 1 & 0 & 1\\
1 & 0 & -1 & 0\\
0 & 1 & 0 & -1\\
\end{array}
\right]
と一致します。
##複数量子ビットのうち一部のみを測定
Quantum Native Dojoで使われている用語の解説をします。
状態空間
量子状態を表すベクトルの集合のこと。[3]
正規直交基底
ベクトル空間において、長さが1(正規)、内積が0(直交)、空間中の全てのベクトルを表すのに必要最低限のベクトルの集合(基底)[4]
1量子ビットの場合は、一例として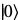
と
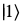である。
射影演算子
以下の条件を満たす演算子P[5]
P^{2} = P \\
P^{\ast} = P
この場合、射影演算子は
|0\rangle\langle0|, |1\rangle\langle1|
である。
ここでn量子ビットのうち1番目の値が0の確率を考えてみましょう。
量子状態を
|\psi\rangle = \sum_{\psi \in \{0,1\}}^{} c_{\psi_{0}\psi_{1}\cdots\psi{n} }|\psi_{0}\psi_{1}\cdots\psi_{n} \rangle
とすると、今求めたいのは
p_0 = \sum_{\psi \in \{0,1\}}^{}|c_{0\psi_{1}\cdots\psi_{n}}|^{2}
の確率pであり、 測定後の状態は
\frac{1}{\sqrt{p_0}}\sum_{\psi \in \{0,1\}}^{} c_{\psi_{0}\psi_{1}\cdots\psi{n} }|\psi_{0}\psi_{1}\cdots\psi_{n} \rangle
です。
早速、２つの量子ビット両方にHゲートとCNOTゲートをかけて、1番目が0の確率を理論的に求めてみましょう。
初期状態が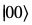
とすると、
|00\rangle \xrightarrow{H_{0}\otimes H_{1}\otimes CNOT_{0,1}}
(\frac{1}{2})^{2}(|00\rangle+|01\rangle+|10\rangle+|11\rangle)
よって、1量子ビット目が0だったら、
|00\rangle \,, |01\rangle
の状態が当てはまるが、それらが求まる確率は
(\frac{1}{2})^{2} * 2 = \frac{1}{2}
それではこれをSympyを用いて求めてみましょう。
#量子状態を生成する。
psi = qapply(CNOT(1, 0)*H(1)*H(0)*Qubit('00'))
from sympy.physics.quantum.qubit import measure_all, measure_partial
#量子状態psiのうち2量子ビットの値を測定する。
measured_state_and_probability = measure_partial(psi, (1,))
#0だった時の状態と、その確率を求める。
measured_state_and_probability[0]
これを実行すると、
が得られます。
左に出てきたのが予想される状態、右がその状態が求められる確率です。これは理論値と合致しています。
参考文献