著作権情報 THE IDOLM@STER™& ©Bandai Namco Entertainment Inc.
この記事はデレステのノーツを再現してみた。の続編です。
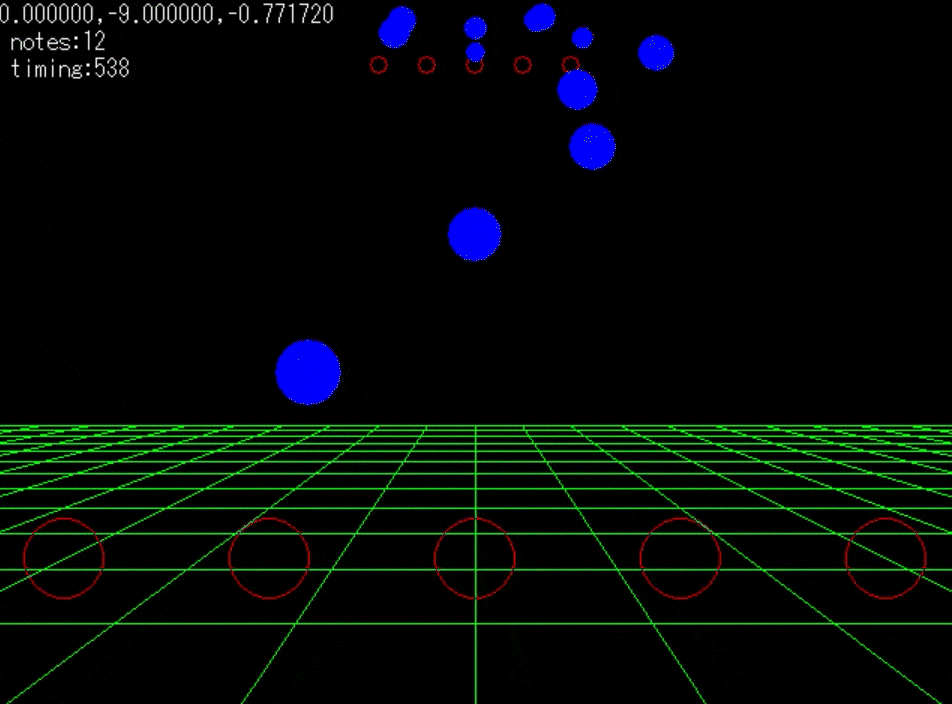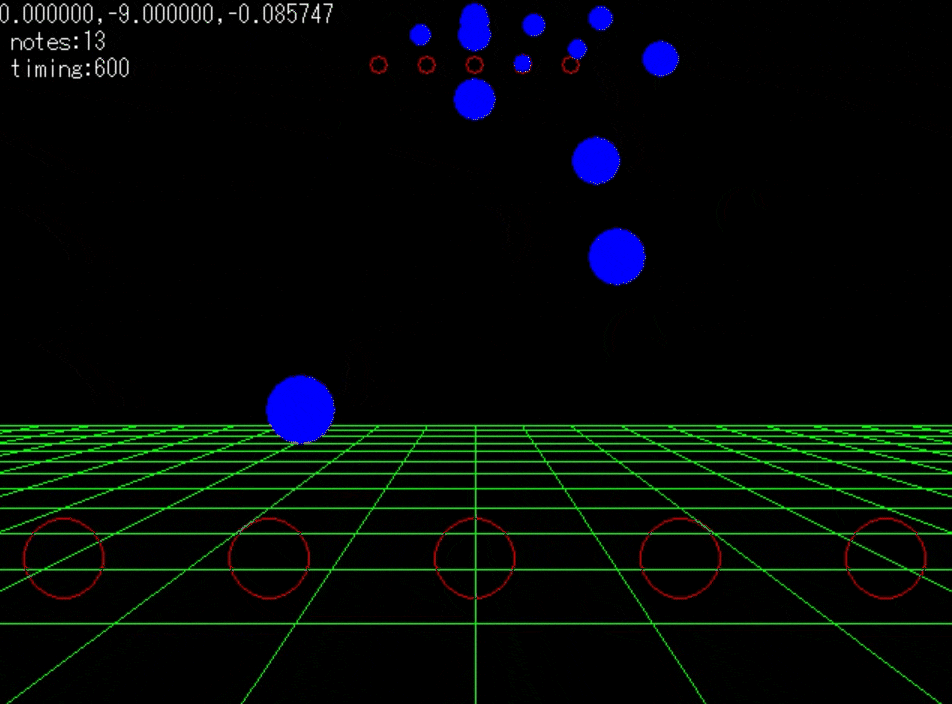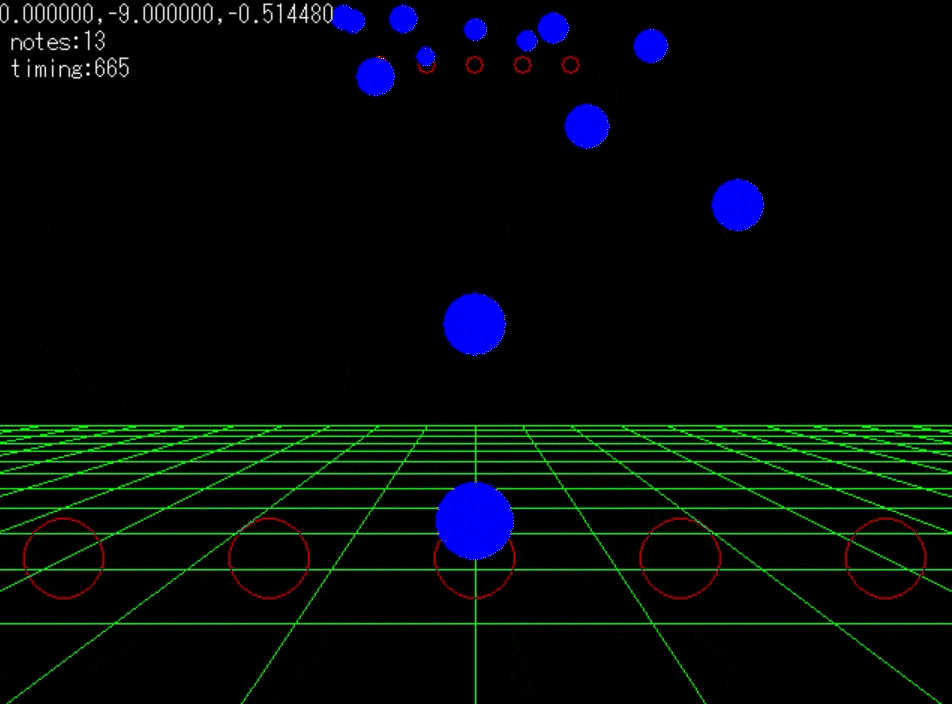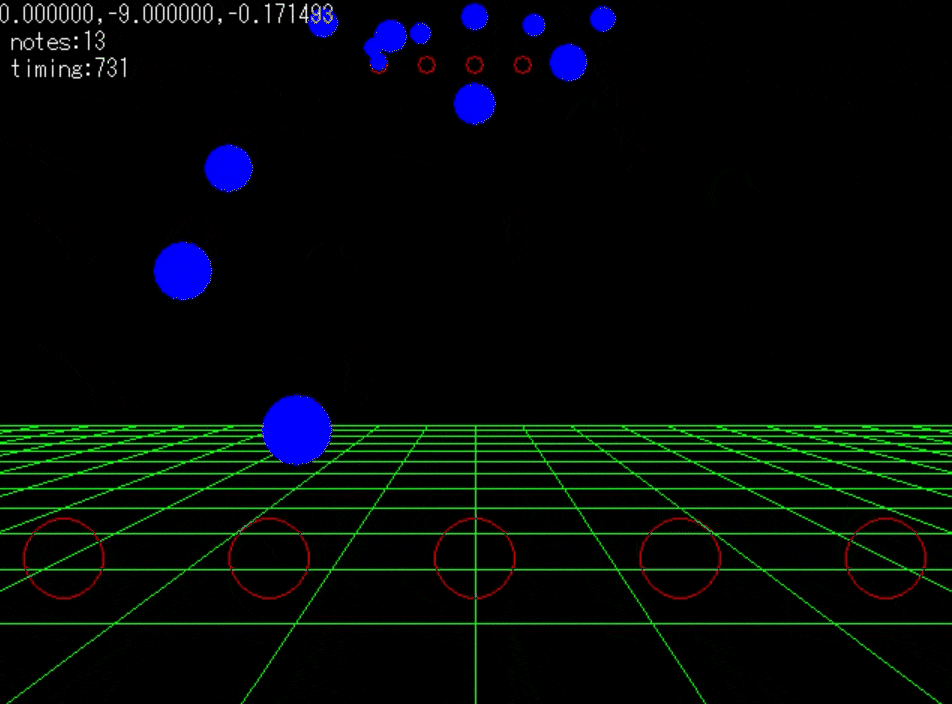
- 3倍速の動作動画である。
無駄を省きシンプルにする
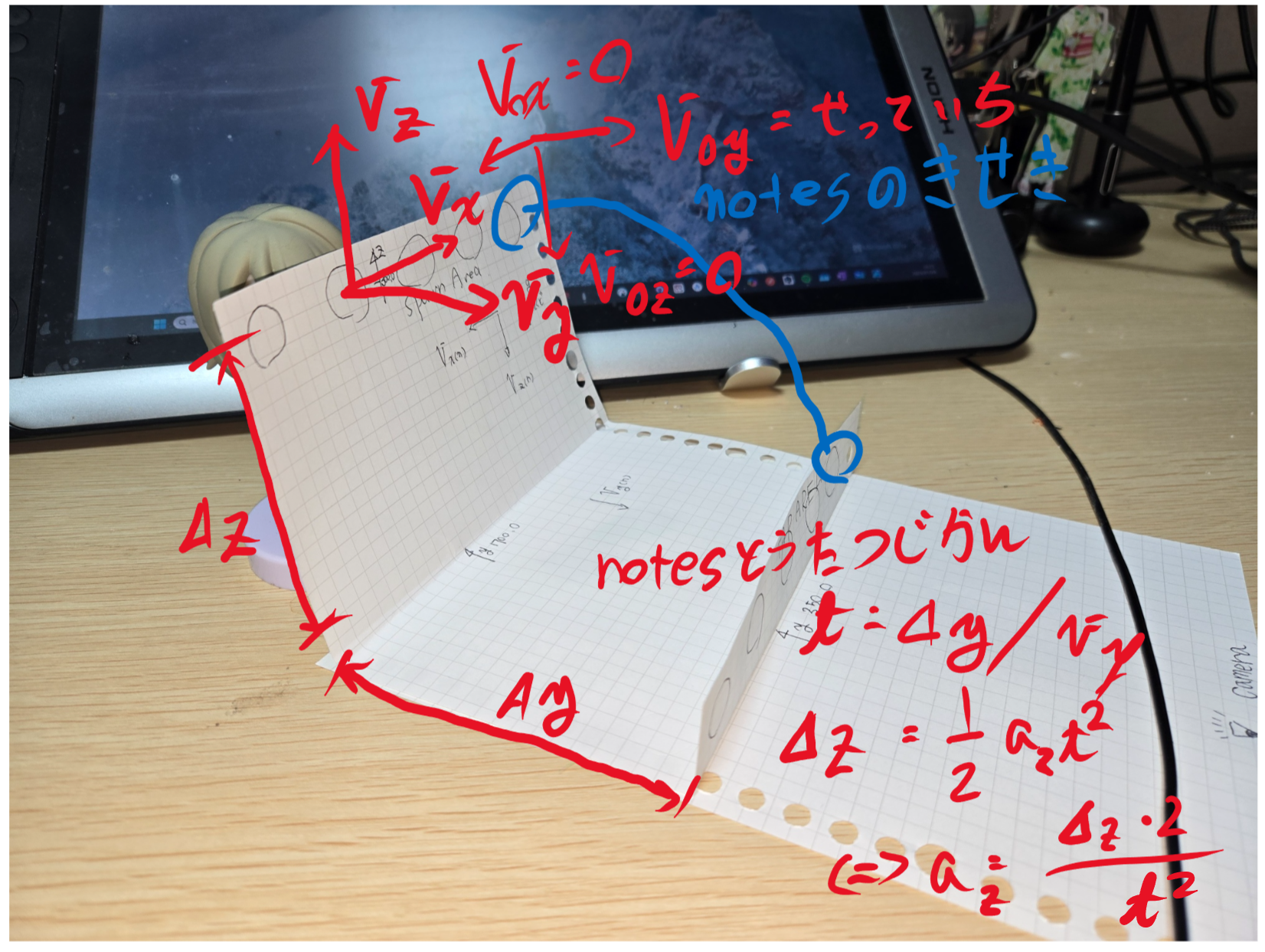
前回はデレステのノーツ表現空間を3Dとして捉え、実際にノーツを大砲の玉と捉えて速度成分と、加速度を個々に計算していた。大きな計算量の無駄が生じていることに気がついた。
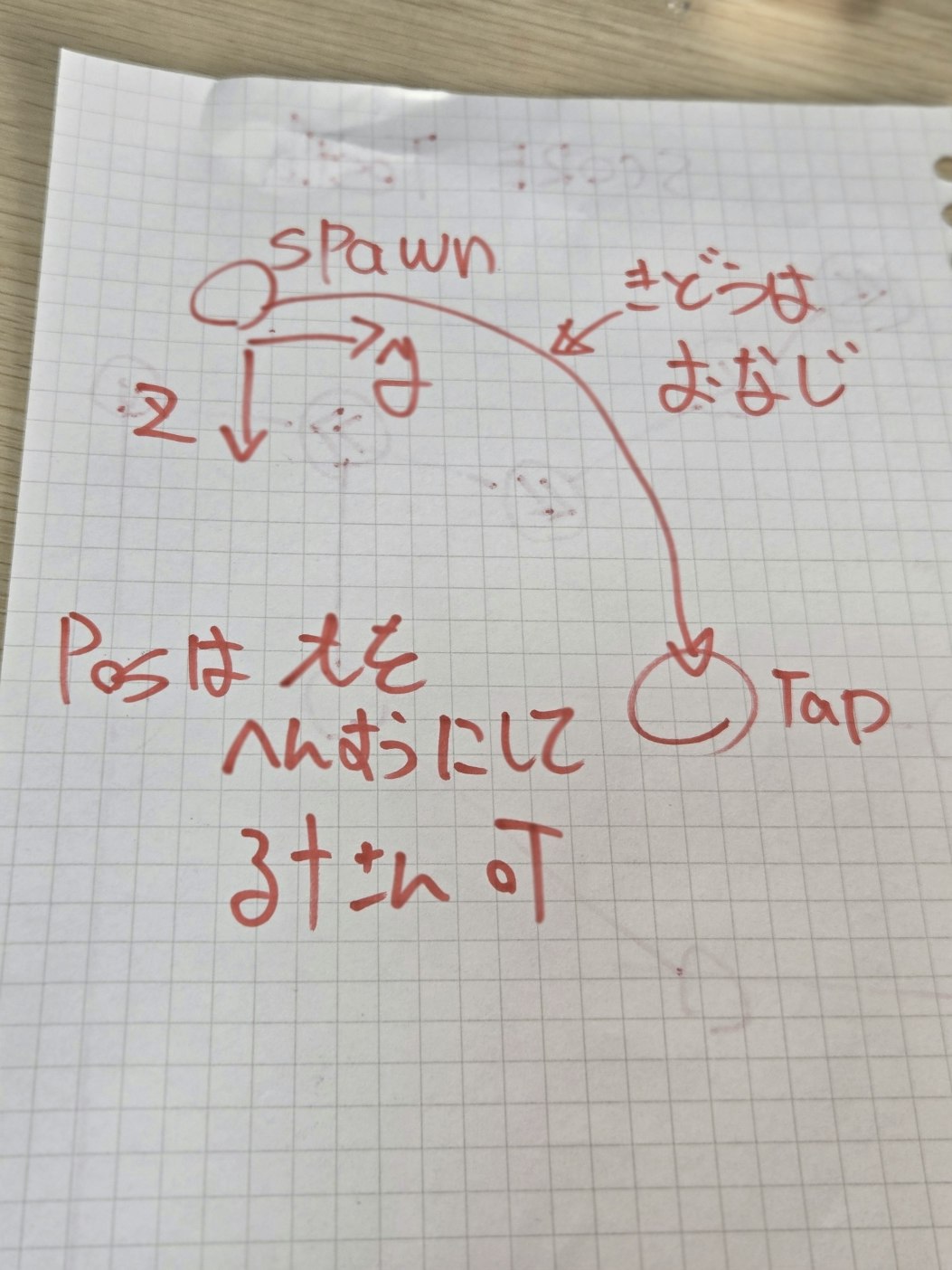
そうノーツ速度はレベルに置いて固定値なので加速度も変化することはない。つまり、ノーツのZY成分における軌道はすべて同一なのである。一回何らかの配列に計算結果を入れてやれば、いちいち再計算する必要はないのだ。
あと、加速度をよしなに計算してタップの領域にいれる手法を取る場合、誤差の話が必ずつきまとう。極端な話、ノーツ速度を凄まじく大きくした場合、Z成分の加速度はtが小さくなる方向に移動するので正の無限に発散する。
HSPに関して触り始めて数日なのでどのくらいの精度を持って演算できるのかは、まだ把握しきれていないが、これは何もHSPに限ったことではなく別の言語で実装した場合も同じ話である。
3次元は2次元より複雑である
これは言わずもがな、次元が一つ増えるのであるから当然の話しである。
あとレベル作成ツールにおいて実装はシンプルな方が良い。当然3Dより2Dの方が良いのだ。
そう、やはりレベル作成ツールに置いても3次元よりもこのように2次元の配置にしたほうがレベル作成者も、実装としてもシンプルでわかりやすいものになる。
しかし実際にプレイする画面においてはノーツは擬似的であっても3次元空間である。さてどうするか?
次元を上げる
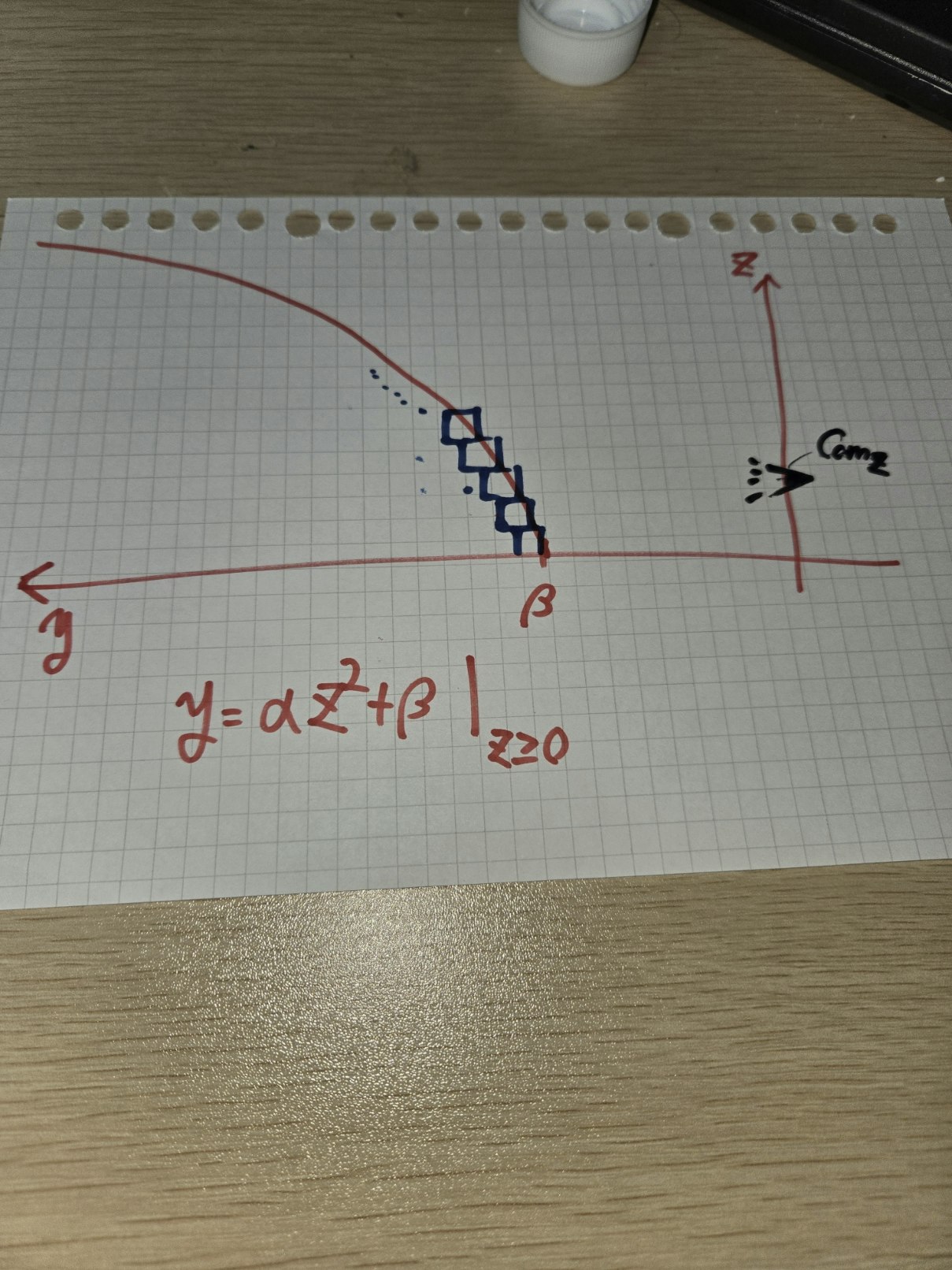
この場合のYZ曲線は円になるが曲線であれば何でも構わない、手元にペットボトルしかなかったので
こうしてやれば良い。
この手法の良いところは、前回の手法ではXYZ成分の座標をtを変数として計算していたが、Unityにおいて適当な円柱でも何でも用意して、そこにテキスチャとして譜面を貼り付ける。
ノーツ速度を2倍にする場合はテキスチャをY方向に2倍して貼り付け回転速度なりスクロール速度を2倍にすればいいだけになることである。座標変換が適切にさえ行われればレベル作成ツールでは2次元のデータとして扱い、プレイ時に3次元の奥行きを表現することが可能になるのだ。レベル作成ツールもプレイアプリの実装もよりシンプルになる。
ちなみにこれに似た構造を持つおもちゃを貴方は人生の中で一度は見ているはずだ。
しかしHSPでの実装では苦労した
理由としては単純でYZ軸に円でも楕円でも何でも良いが曲線になっている物体(円柱とか)にテクスチャを貼り付ける機能が見当たらなかったからである。直方体なら貼れるよということで、ここでティンと来た人は鋭い。
要は階段状に直方体を積み上げていく方式になる。この手法を取らざるを得なかったために見てくれは非常に悪くなってしまった。ただUnityに置いてXZ曲線をX軸の有限範囲で定義した取った物体(例えば円柱)にテクスチャが貼れないとかはありえねえと思うのでこれはモックの段階で言語の仕様上仕方ないことであり、本番ではこの手法でレベル作成ツールやプレヤーを作成しようと思う。
モックとしてはある程度の完成度かな
一応、考えつくアイデアとしてはこんなもんで行けそうだなという感覚ではある。
ということで一応mainにマージしておいた。寝ればまた何か思いつくかもしれないので寝ることにする。